Modèles plus avancés
1. Modèle probabiliste
1.1. Principe
Soit R et NR représentent respectivement la pertinence et la non-pertinence (ou de façon équivalente, l’ensemble de document pertinents et l’ensemble non-pertinent).
L’idée de base dans un modèle probabiliste est de tenter de déterminer les probabilités P(R|D) et P(NR|D) pour une requête donnée. Ces deux probabilités signifient respectivement : si on retrouve le document D, quelle est la probabilité qu’on obtient l’information pertinente et non-pertinente.
Dans un premier temps, travaillons dans le contexte suivant :
On ne considère que la présence et l’absence de termes dans les documents et dans les requêtes comme des caractéristiques observables. Autrement dit, les termes ne sont pas pondérés, mais prennent seulement les valeurs 0 (absent) ou 1 (présent).
On suppose qu’on a une requête fixe. On tente de déterminer les caractéristiques de R et NR pour cette requête donnée.
Donc, implicitement, P(R|D) et P(NR|D) correspondent plutôt à P(RQ|D) et P(NRQ|D) pour la requête Q, mais cet index peut être ignoré pour l’instant.
Si on peut calculer ces deux probabilités, alors on pourra classer les documents selon ces deux probabilités, ou selon la fonction (odd) suivant qui compare les deux probabilités :
O(D) = P(R|D) / P(NR|D)
Plus O(D) est élevée pour un document, plus ce document doit être classé en haut.
Cependant, les deux probabilités nécessaires ne sont pas directement calculables. Ainsi, on utilise le théorème de Bayes:
P(R|D) = P(D|R) P(R) / P(D)
P(NR|D) = P(D|NR) P(NR) / P(D)
où P(D|R) = la probabilité que D fait partie de l’ensemble pertinent,
P(R) = la probabilité de pertinence, c’est-à-dire, si on choisit un document au hasard dans le corpus, la chance de tomber sur un document pertinent ;
P(D) = la probabilité que le document soit choisi (si on prend au hasard un document dans le corpus, la chance de tomber sur D).
Appliquons dans O(D),nous avons :
O(D) = P(R|D) / P(NR|D) = [P(D|R) P(R)] / [P(D|NR) P(NR)]
Comme pour la même requête, P(R) et P(NR) sont des constantes. Ainsi, nous pouvons ré-exprimer O(D) comme suit :
O(D) µ P(D|R) / P(D|NR)
(O(D) est proportionnelle à P(D|R) / P(D|NR)).
Étant donné que l’objectif de la RI est de déterminer le rang des documents, on peut très bien utiliser P(D|R) / P(D|NR) à la place de O(D) exacte. Donc, définissons O(D) comme P(D|R) / P(D|NR).
1.2. Hypothèse d’indépendance et le modèle de recherche indépendant
Comment estimer P(D|R) et P(D|NR)? En général, on décompose le document en un ensemble de "événements". Un événement dénote soit la présence ou l'absence d'un terme dans ce document, c’est-à-dire une série de (ti = xi) où xi est 0 ou 1 qui représentent l’absence et la présence du terme. Ainsi :
P(D|R) = P(t1=x1, t2=x2, t3=x3, … |D)
P(D|R) = P(t1=x1, t2=x2, t3=x3, … |NR)
où ti=xi correspond à la présence ou l’absence du terme ti dans le document D.
Dans la théorie de probabilité, on sait que la probabilité de la combinaison de plusieurs événements ensemble doit être déterminée comme suit :
P(a, b, c, d …|R) = P(a|R) * P(b|a,R) * P(c|a,b,R) * P(d|a,b,c,R) * …
C’est-à-dire qu’il faut tenir compte des dépendances entre les événements, représentées dans cette formules par des probabilités conditionnelles. Il est vrai que dans le contexte de RI, les présences et les absences de termes sont dépendants. Par exemple, si le terme « informatique » apparaît dans un document, il y a plus de chance que le terme « ordinateur » apparaît aussi. Ainsi, nous avons :
P(ordinateur=1 | informatique=1) > P(ordinateur=1)
Seulement, si on doit tenir compte de toutes les dépendances, le calcul de P(D|R) et de P(D|NR) sera très complexe, car il faut tenir compte des dépendances suivantes :
P(t2=x2 | t1=x1,R), P(t3=x3 | t1=x1, t2=x2,R), etc.
Si on veut estimer ces probabilités, on aura besoin d’un grand ensemble de documents jugés pertinents pour l’entraînement, ce qui n’est pas disponible. Ainsi, l’hypothèse d’indépendance est supposée pour simplifier le calcul :
Hypothèse d'indépendance: on suppose que les événements liés à différents termes sont indépendants.
Ainsi:
P(D|R) = Õ (ti=xi)ÎD P(ti = xi | R),
et
P(D|NR) = Õ (ti=xi)ÎD P(ti = xi | NR).
Exemple
Soit un document contient t1, t3, t5, et que l'ensemble de termes connus du système est {t1, t2, t3, t4, t5, t6}. Alors:
D = (t1=1, t2=0, t3=1, t4=0, t5=1, t6=0).
Ainsi, :
P(D|R) = P(t1=1|R)* P(t2=0|R)* P(t3=1|R)* P(t4=0|R)* P(t5=1|R)* P(t6=0|R)
L’expression
P(D|R) = Õ (ti=xi)ÎD P(ti = xi | R),
peut être ré-écrite comme suit :
P(D|R) = Õ ti P(ti = 1 | R)xi P(ti = 0 | R)(1-xi)
où ti correspond à n’importe quel terme connu du système.
Par exemple, notre exemple sera transformé en :
P(D|R) = P(t1=1|R)1 * P(t1=0|R)0
* P(t2=1|R)0 * P(t2=0|R)1 * P(t3=1|R)1*
P(t3=0|R)0
* P(t4=1|R)0 * P(t4=0|R)1 * P(t5=1|R)1 * P(t5=0|R)0 * P(t6=1|R)0 * P(t6=0|R)1
La question clé est donc réduite à l’estimation de P(ti = xi | R) et P(ti = xi | NR), ce qui est beaucoup plus faisable. Pour cela, on doit idéalement disposer d'un ensemble d'échantillons de documents déjà jugés pour une requête. Avec ces échantillons, il est possible d'estimer P(ti = xi | R) et P(ti = xi | NR) où R et NR correspondent maintenant respectivement à l’ensemble de document pertinents et non-pertinents parmi les échantillons. Il suffit de construire la table de distribution suivante pour chaque terme ti:
|
#doc. pert. contenant ti |
#doc. pert. ne contenant pas ti |
#doc. pert. |
|
#doc. non-pert. contenant ti |
#doc. non-pert. ne contenant pas ti |
#doc. non-pert. |
|
#doc. contenant ti |
#doc. ne contenant pas ti |
#échantillons |
Supposons qu’on a les valeurs suivantes pour ti:
|
ri |
n - ri |
n |
|
Ri - ri |
N-Ri – n + ri |
N-n |
|
Ri |
N-Ri |
N |
On peut donc obtenir:
pi = P(ti=1|R)
= ![]() ; (1-pi)
= P(ti =0|R) =
; (1-pi)
= P(ti =0|R) = ![]() ;
;
qi = P(ti
=1|NR) = ![]() ; (1-qi)
= P(ti =0|NR) =
; (1-qi)
= P(ti =0|NR) = ![]() ;
;
Ici, pour simplifier les formules, on dénote P(ti=1|R) par pi, P(ti =0|R) par (1-pi), et P(ti =1|NR) par qi, P(ti =0|NR) par (1-qi).
Revenons à O(D), nous avons alors :
O(D) = P(D|R) / P(D|NR)
= 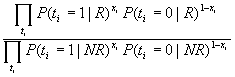
= 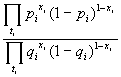
Définissions g(D) comme log O(D), on a :
g(D) = ![]()
=![]()
Remarquons que la partie ![]() ne dépend pas du document (i.e. xi). C’est
la constante pour n’importe quel document. On peut donc la dénoter comme C.
Donc :
ne dépend pas du document (i.e. xi). C’est
la constante pour n’importe quel document. On peut donc la dénoter comme C.
Donc :
g(D) = ![]()
Nous avons encore :
wi = ![]() =
= 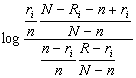 =
= 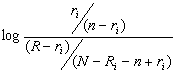
On peut considérer cette fonction comme le poids du terme ti. Ainsi, le poids pour un document est déterminé par p(D) µ g(D):
p(D)
= ![]()
Extension à une autre requête
Pour étendre cette évaluation à une nouvelle requête, on utilise la formule suivante :
pi(D)
= ![]()
où yi est le poids du terme i dans la requête j.
Simplifications
La formule de Robertson-Sparck Jones est souvent utilisée dans des approches probabilistes en RI. Elle est simplement un adoucissement (smoothing) de g(D) décrite précédemment. Elle consiste à déterminer le poids d'un terme t:
wi
= 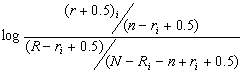
Il y a des simplifications plus sévères.
1. On suppose que la probabilité qu'un terme apparaît dans la classe pertinente est une constante: P(t=1|R) = 0.5, et P(t=0|R) = 0.5
La probabilité d'apparition dans la classe non-pertinent est: P(t=1|N) = n/N, où n est le nombre de document contenant le terme t, et N est le nombre total de document. On a donc aussi P(t=0|N) = 1- P(t=1|N) = 1- n/N
Évidemment, cette estimation est très grossière. Il serait nécessaire de les ajuster.
2. Un ajustement consiste à utiliser le nombre de documents retrouvés, ce qui correspond au principe de "pseudo-relevance feedback". Cette estimation est comme suit:
P(t=1|R) = v/V, où v est le nombre de documents retrouvés contenant t;
P(t=1|N) = (n-v)/(N-V)
3. Dans cette estimation, on observe que (1) quand v=0, P(t=1|R)=0; (2) si V est petit (e.g. 1), P(t=1|R) est très grande. Étant donné les erreurs qui existent dans cette estimation, on ne veut pas faire des estimations aussi draconiennes. Ainsi, les formules suivantes sont souvent utilisées. Cela correspond au principe de "smoothing" dans la reconnaissance de parôle, par exe,ple.
P(t=1|R) = (v+0.5)/(V+1)
P(t=1|N) = (n-v+0.5)/(N-V+1)
4. Ou bien les formules suivantes, qui consistent à remplacer 0.5 par (n/N):
P(t=1|R) = (v + n/N) / (V+1)
P(t=1|N) = (n-v + n/N)/(N-V+1)
Prise en compte des
pondérations de termes
Dans les modèles probabilistes précédents, on considère un poids binaire pour chaque terme (0 ou 1). Dans une approche proposé par Croft et al., on propose de tenir compte d'une pondération non-binaire des termes.
Soit odd (ici, on tient compte de P(R) et P(N)):
h(t=1) = [P(t=1|R)*P(R)] / ]P(t=1|N)*P(N)]
Une "expectation" de h est:
E(h(t)) = P(t=1|D) h(t=1) + P(t=0|D)
h(t=0)
On suppose que h(t=0) = 0. Donc:
E(h(t)) = P(t=1|D) h(t=1)
En particulier, P(t=1|D) est calculée comme suit:
P(t=1|D) = K + (1-K)*n(t)
Où n(t) = w(t) / Maxt w(t) est une pondération de terme normalisée.
Finalement, l'expectation d'un document à appartenir dans la classe de "pertinent" est calculée comme suit:
E(D) = å tÎ D E(h(t))
Rérérences
Livre de - R. Baeza-Yates, B. Ribeiro-Neto, Modern Information Retrieval, Addison-Wesley, 1999.
Le livre de Van Rijsbergen - Information retrieval (en ligne).