Getting Started¶
These tutorials do not attempt to make up for a graduate or undergraduate course in machine learning, but we do make a rapid overview of some important concepts (and notation) to make sure that we’re on the same page. You’ll also need to download the datasets mentioned in this chapter in order to run the example code the up-coming tutorials.
Datasets¶
MNIST Dataset¶
The MNIST dataset consists of handwritten digit images and it is divided in 60 000 examples for the training set and 10 000 examples for testing. In many papers as well as in this tutorial, the official training set of 60 000 is divided into an actual training set of 50 000 examples and 10 000 validation examples (for selecting hyper-parameters like learning rate and size of the model). All digit images have been size-normalized and centered in a fixed size image of 28 x 28 pixels. In the original dataset each pixel of the image is represented by a value between 0 and 255, where 0 is black, 255 is white and anything in between is a different shade of grey.
Here are some examples of MNIST digits:


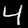

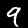
For convenience we pickled the dataset to make it easier to use in python. It is available for download here. The pickled file represents a tuple of 3 lists : the training set, the validation set and the testing set. Each of the three lists is a pair formed from a list of images and a list of class labels for each of the images. An image is represented as numpy 1-dimensional array of 784 (28 x 28) float values between 0 and 1 (0 stands for black, 1 for white). The labels are numbers between 0 and 9 indicating which digit the image represents. When using the dataset, we usually divide it in minibatches (see Stochastic Gradient Descent). The code block below shows how to load the dataset and how to divide it in minibatches of a given size :
import cPickle, gzip, numpy # Load the dataset f = gzip.open('mnist.pkl.gz','rb') train_set, valid_set, test_set = cPickle.load(f) f.close() # make minibatches of size 20 batch_size = 20 # sized of the minibatch # Dealing with the training set # get the list of training images (x) and their labels (y) (train_set_x, train_set_y) = train_set # initialize the list of training minibatches with empty list train_batches = [] for i in xrange(0, len(train_set_x), batch_size): # add to the list of minibatches the minibatch starting at # position i, ending at position i+batch_size # a minibatch is a pair ; the first element of the pair is a list # of datapoints, the second element is the list of corresponding # labels train_batches = train_batches + \ [(train_set_x[i:i+batch_size], train_set_y[i:i+batch_size])] # Dealing with the validation set (valid_set_x, valid_set_y) = valid_set # initialize the list of validation minibatches valid_batches = [] for i in xrange(0, len(valid_set_x), batch_size): valid_batches = valid_batches + \ [(valid_set_x[i:i+batch_size], valid_set_y[i:i+batch_size])] # Dealing with the testing set (test_set_x, test_set_y) = test_set # initialize the list of testing minibatches test_batches = [] for i in xrange(0, len(test_set_x), batch_size): test_batches = test_batches + \ [(test_set_x[i:i+batch_size], test_set_y[i:i+batch_size])] # accessing training example i of minibatch j image = training_set[j][0][i] label = training_set[j][1][i]
Notation¶
Dataset notation¶
We label data sets as 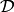 . When the distinction is important, we
indicate train, validation, and test sets as:
. When the distinction is important, we
indicate train, validation, and test sets as: 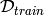 ,
,
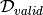 and
and 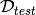 . The validation set
is used to perform model selection and hyper-parameter selection, whereas
the test set is used to evaluate the final generalization error and
compare different algorithms in an unbiased way.
. The validation set
is used to perform model selection and hyper-parameter selection, whereas
the test set is used to evaluate the final generalization error and
compare different algorithms in an unbiased way.
The tutorials mostly deal with classification problems, where each data set
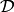 is an indexed set of pairs
is an indexed set of pairs 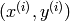 . We
use superscripts to distinguish training set examples:
. We
use superscripts to distinguish training set examples:  is thus the i-th training example of dimensionality
is thus the i-th training example of dimensionality 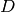 . Similarly,
. Similarly,
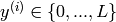 is the i-th label assigned to input
is the i-th label assigned to input
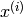 . It is straightforward to extend these examples to
. It is straightforward to extend these examples to
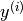 that has other types (e.g. Gaussian for regression,
or groups of multinomials for predicting multiple symbols).
that has other types (e.g. Gaussian for regression,
or groups of multinomials for predicting multiple symbols).
Math Conventions¶
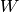 : upper-case symbols refer to a matrix unless specified otherwise
: upper-case symbols refer to a matrix unless specified otherwise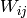 : element at i-th row and j-th column of matrix
: element at i-th row and j-th column of matrix 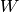
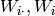 : vector, i-th row of matrix
: vector, i-th row of matrix 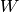
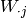 : vector, j-th column of matrix
: vector, j-th column of matrix 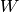
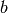 : lower-case symbols refer to a vector unless specified otherwise
: lower-case symbols refer to a vector unless specified otherwise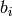 : i-th element of vector
: i-th element of vector 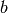
List of Symbols and acronyms¶
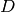 : number of input dimensions.
: number of input dimensions. : number of hidden units in the
: number of hidden units in the 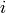 -th layer.
-th layer.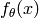 ,
, 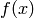 : classification function associated with a model
: classification function associated with a model 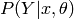 , defined as
, defined as 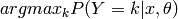 .
Note that we will often drop the
.
Note that we will often drop the 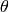 subscript.
subscript.- L: number of labels.
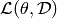 : log-likelihood
: log-likelihood  of the model defined by parameters
of the model defined by parameters 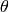 .
.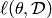 empirical loss of the prediction function f
parameterized by
empirical loss of the prediction function f
parameterized by 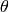 on data set
on data set  .
.- NLL: negative log-likelihood
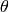 : set of all parameters for a given model
: set of all parameters for a given model
Python Namespaces¶
Tutorial code often uses the following namespaces:
import theano
import theano.tensor as T
A Primer on Supervised Optimization for Deep Learning¶
What’s exciting about Deep Learning is largely the use of unsupervised learning of deep networks. But supervised learning also plays an important role. The utility of unsupervised pre-training is often evaluated on the basis of what performance can be achieved after supervised fine-tuning. This chapter reviews the basics of supervised learning for classification models, and covers the minibatch stochastic gradient descent algorithm that is used to fine-tune many of the models in the Deep Learning Tutorials.
Learning a Classifier¶
Zero-One Loss¶
The models presented in these deep learning tutorials are mostly used as
for classification. The objective in training a classifier is to minimize the number
of errors (zero-one loss) on unseen examples. If 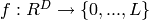 is the prediction function, then this loss can be written as:
is the prediction function, then this loss can be written as:
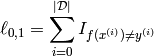
where either 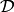 is the training
set (during training)
or
is the training
set (during training)
or 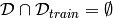 (to avoid biasing the evaluation of validation or test error).
(to avoid biasing the evaluation of validation or test error). 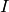 is the
indicator function defined as:
is the
indicator function defined as:
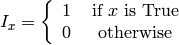
In this tutorial, 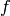 is defined as:
is defined as:
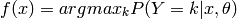
In python, using Theano this can be written as :
# zero_one_loss is a Theano variable representing a symbolic
# expression of the zero one loss ; to get the actual value this
# symbolic expression has to be compiled into a Theano function (see
# the Theano tutorial for more details)
zero_one_loss = T.sum(T.neq(T.argmax(p_y_given_x),y))
Negative Log-Likelihood Loss¶
Since the zero-one loss is not differentiable, optimizing it for large models (thousands or millions of parameters) is prohibitively expensive (computationally). We thus maximize the log-likelihood of our classifier given all the labels in a training set.
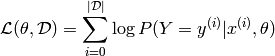
The likelihood of the correct class is not the same as the number of right predictions, but from the point of view of a randomly initialized classifier they are pretty similar. Remember that likelihood and zero-one loss are different objectives; you should see that they are corralated on the validation set but sometimes one will rise while the other falls, or vice-versa.
Since we usually speak in terms of minimizing a loss function, learning will thus attempt to minimize the negative log-likelihood (NLL), defined as:
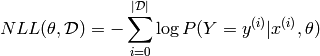
The NLL of our classifier is a differentiable surrogate for the zero-one loss, and we use the gradient of this function over our training data as a supervised learning signal for deep learning of a classifier.
This can be computed using the following line of code :
# NLL is a symbolic variable ; to get the actual value of NLL, this symbolic
# expression has to be compiled into a Theano function (see the Theano
# tutorial for more details)
NLL = -T.sum(T.log(p_y_given_x)[y.shape[0],y])
# note on syntax: T.arange(y,shape[0]) is a vector of integers [0,1,2,...,len(y)].
# Indexing a matrix M by the two vectors [0,1,...,K], [a,b,...,k] returns the
# elements M[0,a], M[1,b], ..., M[K,k] as a vector. Here, we use this
# syntax to retrieve the log-probability of the correct labels, y.
Stochastic Gradient Descent¶
What is ordinary gradient descent? it is a simple algorithm in which we repeatedly make small steps downward on an error surface defined by a loss function of some parameters. For the purpose of ordinary gradient descent we consider that the training data is rolled into the loss function. Then the pseudocode of this algorithm can be described as :
# GRADIENT DESCENT
while True:
loss = f(params)
d_loss_wrt_params = ... # compute gradient
params -= learning_rate * d_loss_wrt_params
if <stopping condition is met>:
return params
Stochastic gradient descent (SGD) works according to the same principles as ordinary gradient descent, but proceeds more quickly by estimating the gradient from just a few examples at a time instead of the entire training set. In its purest form, we estimate the gradient from just a single example at a time.
# STOCHASTIC GRADIENT DESCENT
for (x_i,y_i) in training_set:
# imagine an infinite generator
# that may repeat examples (if there is only a finite training set)
loss = f(params, x_i, y_i)
d_loss_wrt_params = ... # compute gradient
params -= learning_rate * d_loss_wrt_params
if <stopping condition is met>:
return params
The variant that we recommend for deep learning is a further twist on stochastic gradient descent using so-called “minibatches”. Minibatch SGD works identically to SGD, except that we use more than one training example to make each estimate of the gradient. This technique reduces variance in the estimate of the gradient, and often makes better use of the hierarchical memory organization in modern computers.
for (x_batch,y_batch) in train_batches:
# imagine an infinite generator
# that may repeat examples
loss = f(params, x_batch, y_batch)
d_loss_wrt_params = ... # compute gradient using theano
params -= learning_rate * d_loss_wrt_params
if <stopping condition is met>:
return params
There is a tradeoff in the choice of the minibatch size 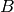 . The
reduction of variance and use of SIMD instructions helps most when increasing
. The
reduction of variance and use of SIMD instructions helps most when increasing
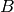 from 1 to 2, but the marginal improvement fades rapidly to nothing.
With large
from 1 to 2, but the marginal improvement fades rapidly to nothing.
With large 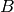 , time is wasted in reducing the variance of the gradient
estimator, that time would be better spent on additional gradient steps.
An optimal
, time is wasted in reducing the variance of the gradient
estimator, that time would be better spent on additional gradient steps.
An optimal 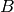 is model-, dataset-, and hardware-dependent, and can be
anywhere from 1 to maybe several hundreds. In the tutorial we set it to 20,
but this choice is almost arbitrary (though harmless). All code-blocks
above show pseudocode of how the algorithm looks like. Implementing such
algorithm in Theano can be done as follows :
is model-, dataset-, and hardware-dependent, and can be
anywhere from 1 to maybe several hundreds. In the tutorial we set it to 20,
but this choice is almost arbitrary (though harmless). All code-blocks
above show pseudocode of how the algorithm looks like. Implementing such
algorithm in Theano can be done as follows :
# Minibatch Stochastic Gradient Descent
# assume loss is a symbolic description of the loss function given
# the symbolic variables params (shared variable), x_batch, y_batch;
# compute gradient of loss with respect to params
d_loss_wrt_params = T.grad(loss, params)
# compile the MSGD step into a theano function
updates = { params: params - learning_rate * d_loss_wrt_params}
MSGD = theano.function([x_batch,y_batch], loss, updates = updates)
for (x_batch, y_batch) in train_batches:
# here x_batch and y_batch are elements of train_batches and
# therefore numpy arrays; function MSGD also updates the params
print('Current loss is ', MSGD(x_batch, y_batch))
if <stopping condition is met>:
return params
Regularization¶
There is more to machine learning than optimization. When we train our model from data we are trying to prepare it to do well on new examples, not the ones it has already seen. The training loop above for MSGD does not take this into account, and may overfit the training examples. A way to combat overfitting is through regularization. There are several techniques for regularization; the ones we will explain here are L1/L2 regularization and early-stopping.
L1 and L2 regularization¶
L1 and L2 regularization involve adding an extra term to the loss function, which penalizes certain parameter configurations. Formally, if our loss function is:
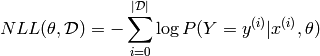
then the regularized loss will be:
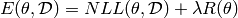
or, in our case
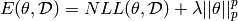
where
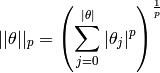
which is the 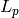 norm of
norm of 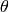 .
. 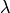 is a hyper-parameter which
controls the relative importance of the regularization parameter. Commonly used values for p
are 1 and 2, hence the L1/L2 nomenclature. If p=2, then the regularizer is
also called “weight decay”.
is a hyper-parameter which
controls the relative importance of the regularization parameter. Commonly used values for p
are 1 and 2, hence the L1/L2 nomenclature. If p=2, then the regularizer is
also called “weight decay”.
In principle, adding a regularization term to the loss will encourage smooth
network mappings in a neural network (by penalizing large values of the
parameters, which decreases the amount of nonlinearity that the
network models). More intuitively, the two terms (NLL and 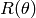 )
correspond to modelling the data well (NLL) and having “simple” or “smooth”
solutions (
)
correspond to modelling the data well (NLL) and having “simple” or “smooth”
solutions (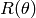 ). Thus, minimizing the sum of both will, in
theory, correspond to finding the right trade-off between the fit to the
training data and the “generality” of the solution that is found. To follow
Occam’s razor principle, this minimization should find us the simplest
solution (as measured by our simplicity criterion) that fits the training
data.
). Thus, minimizing the sum of both will, in
theory, correspond to finding the right trade-off between the fit to the
training data and the “generality” of the solution that is found. To follow
Occam’s razor principle, this minimization should find us the simplest
solution (as measured by our simplicity criterion) that fits the training
data.
Note that the fact that a solution is “simple” does not mean that it will
generalize well. Empirically, it was found that performing such regularization
in the context of neural networks helps with generalization, especially
on small datasets.
The code block below shows how to compute the loss in python when it
contains both a L1 regularization term weighted by 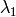 and
L2 regularization term weighted by
and
L2 regularization term weighted by 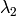
# symbolic Theano variable that represents the L1 regularization term
L1 = T.sum(abs(param))
# symbolic Theano variable that represents the squared L2 term
L2_sqr = T.sum(param**2)
# the loss
loss = NLL + lambda_1 * L1 + lambda_2 * L2
Early-Stopping¶
Early-stopping combats overfitting by monitoring the model’s performance on a validation set. A validation set is a set of examples that we never use for gradient descent, but which is also not a part of the test set. The validation examples are considered to be representative of future test examples. We can use them during training because they are not part of the test set. If the model’s performance ceases to improve sufficiently on the validation set, or even degrades with further optimization, then the heuristic implemented here gives up on much further optimization.
The choice of when to stop is a judgement call and a few heuristics exist***, but these tutorials will make use of a strategy based on a geometrically increasing amount of patience.
# PRE-CONDITION
# params refers to [initialized] parameters of our model
# early-stopping parameters
n_iter = 100 # the maximal number of iterations of the
# entire dataset considered
patience = 5000 # look at this many training examples regardless
patience_increase = 2 # wait this much longer when a new best
# validation error is found
improvement_threshold = 0.995 # a relative improvement of this much is
# considered significant
validation_frequency = 2500 # make this many SGD updates between validations
# initialize cross-validation variables
best_params = None
best_validation_loss = float('inf')
for iter in xrange( n_iter * len(train_batches) ) :
# get epoch and minibatch index
epoch = iter / len(train_batches)
minibatch_index = iter % len(train_batches)
# get the minibatches corresponding to `iter` modulo
# `len(train_batches)`
x,y = train_batches[ minibatch_index ]
d_loss_wrt_params = ... # compute gradient
params -= learning_rate * d_loss_wrt_params # gradient descent
# note that if we do `iter % validation_frequency` it will be
# true for iter = 0 which we do not want
if (iter+1) % validation_frequency == 0:
this_validation_loss = ... # compute zero-one loss on validation set
if this_validation_loss < best_validation_loss:
# improve patience if loss improvement is good enough
if this_validation_loss < best_validation_loss*improvement_threshold:
patience = iter * patience_increase
best_params = copy.deepcopy(params)
best_validation_loss = this_validation_loss
if patience <= iter:
break
# POSTCONDITION:
# best_params refers to the best out-of-sample parameters observed during the optimization
If we run out of batches of training data before running out of patience, then we just go back to the beginning of the training set and repeat.
Note
This algorithm could possibly be improved by using a test of statistical significance rather than the simple comparison, when deciding whether to increase the patience.
Testing¶
After the loop exits, the best_params variable refers to the best-performing model on the validation set. If we repeat this procedure for another model class, or even another random initialization, we should use the same train/valid/test split of the data, and get other best-performing models. If we have to choose what the best model class or the best initialization was, we compare the best_validation_loss for each model. When we have finally chosen the model we think is the best (on validation data), we report that model’s test set performance. That is the performance we expect on unseen examples.
Recap¶
That’s it for the optimization section.
The technique of early-stopping requires us to partition the set of examples into three sets
(training 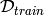 ,
validation
,
validation 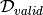 ,
test
,
test 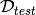 ).
The training set is used for minibatch stochastic gradient descent on the
differentiable approximation of the objective function.
As we perform this gradient descent, we periodically consult the validation set
to see how our model is doing on the real objective function (or at least our
empirical estimate of it).
When we see a good model on the validation set, we save it.
When it has been a long time since seeing a good model, we abandon our search
and return the best parameters found, for evaluation on the test set.
).
The training set is used for minibatch stochastic gradient descent on the
differentiable approximation of the objective function.
As we perform this gradient descent, we periodically consult the validation set
to see how our model is doing on the real objective function (or at least our
empirical estimate of it).
When we see a good model on the validation set, we save it.
When it has been a long time since seeing a good model, we abandon our search
and return the best parameters found, for evaluation on the test set.
