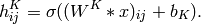Convolutional Neural Networks (LeNet)¶
Note
This section assumes the reader has already read through Classifying MNIST digits using Logistic Regression and mlp. Additionally, it uses the following new Theano functions and concepts: TODO
Motivation¶
Convolutional Neural Networks (CNN) are variants of MLPs which are inspired from biology. From Hubel and Wiesel’s early work on the cat’s visual cortex [Hubel], we know there exists a complex arrangement of cells within the visual cortex. These cells are sensitive to small sub-regions of the input space, called a receptive field, and are tiled in such a way as to cover the entire visual field. These filters are local in input space and are thus better suited to exploit the strong local correlation present in natural images.
Additionally, two basic cell types have been identified: simple cells (S) and complex cells (C). Simple cells (S) respond maximally to specific edge-like stimulus patterns within their receptive field. Complex cells (C) have larger receptive fields and are locally invariant to the exact position of the stimulus.
The visual cortex being the most powerful “vision” system in existence, it seems natural to emulate its behavior. Many such neurally inspired models can be found in the litterature. To name a few: the NeoCognitron [Fukushima], HMAX [Serre] and LeNet-5 [LeCun]. LeNet-5 will be the topic of this tutorial.
The Model¶
Sparse Connectivity¶
CNNs exploit local correlation by enforcing a local connectivity pattern between neurons of adjacent layers. The input hidden units in the i-th layer are connected to a local subset of units in the (i-1)-th layer, which are spatially contiguous. We can illustrate this graphically as follows:
TODO FIGURE
This architecture thus confines the learnt filters to be local. Stacking many such layers leads to filters which become increasingly “global” (i.e spanning a larger region of pixel space) and abstract (as in any MLP).
Going from MLP to convolutional MLP¶
Putting it All Together¶
Note
TODO introduce API for sparse filters
References¶
| [Hubel] | Hubel, D. and Wiesel, T. (1968). Receptive fields and functional architecture of monkey striate cortex. Journal of Physiology (London), 195, 215–243. |
| [Fukushima] | Fukushima, K. (1980). Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics, 36, 193–202. |
| [Serre] | Serre, T., Wolf, L., Bileschi, S., and Riesenhuber, M. (2007). Robust object recog- nition with cortex-like mechanisms. IEEE Trans. Pattern Anal. Mach. Intell., 29(3), 411–426. Member-Poggio, Tomaso. |
| [LeCun] | LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998d). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324. |
Footnotes
| [1] | For clarity, we use the word “unit” or “neuron” to refer to the artificial neuron and “cell” to refer to the biological neuron. |
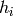 is additionally replicated across the
entire visual field. These “replicated” units form a feature map, which
share the same parametrization, i.e. the same weight vector and the same bias.
Replicating units in this way allows for features to be detected regardless of
their position in the visual field. Each feature map can thus be modeled as the
convolution of a single filter with the input image.
is additionally replicated across the
entire visual field. These “replicated” units form a feature map, which
share the same parametrization, i.e. the same weight vector and the same bias.
Replicating units in this way allows for features to be detected regardless of
their position in the visual field. Each feature map can thus be modeled as the
convolution of a single filter with the input image.![o[n] = f[n]*g[n] = \sum_{u=-\infty}^{\infty} f[u] g[u-n] = \sum_{u=-\infty}^{\infty} f[n-u] g[u]](_images/math/45513e64a977c246dd75b437cc2111649886ab7f.png) .
This can be extended to 2D as follows:
.
This can be extended to 2D as follows:
![o[m,n] = f[m,n]*g[m,n] = \sum_{u=-\infty}^{\infty} \sum_{v=-\infty}^{\infty} f[u,v] g[u-m,v-n]](_images/math/5aa608f746bb0f7f755520e47253dab37a3b0923.png) .
.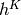 , where
, where
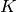 is the index of the feature map (Important: not to be confused
with the notation
is the index of the feature map (Important: not to be confused
with the notation 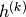 , referring to the k-th hidden layer). Each
feature map
, referring to the k-th hidden layer). Each
feature map 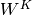 and bias
and bias 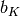 .
Note that the matrix
.
Note that the matrix 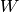 is a matrix whose entries
is a matrix whose entries
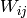 refer to the weight connecting unit
refer to the weight connecting unit 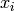 . For
CNNs,
. For
CNNs, 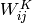 from the K-th feature
map to the input pixel with coordinates (i,j). A CNN layer is thus fully
determined by the set of all such matrices,
from the K-th feature
map to the input pixel with coordinates (i,j). A CNN layer is thus fully
determined by the set of all such matrices, 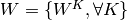 and
the bias vector
and
the bias vector 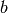 .
.