IFT1227 Architecture des ordinateurs I (Hiver 2008)
Devoir 1
Par groupe 2.
Tout plagiat sera sanctionné selon les règlements de la faculté
Date de remise : vendredi 8 février 2008, 10h30 à votre démonstrateur.
Question 1
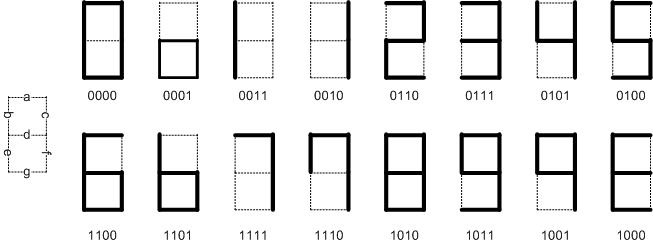
Les affichages d’une sortie à
7-segments, comme les chiffres des calculatrices, sont décrites dans la figure
suivante. Les sept segments sont numérotés de 1 à 7. Dessiner un circuit qui
prend en entrée un nombre binaire de 4-bits et produit en sortie le signal de
contrôle pour des segments d et g
. Un 0 en sortie éteint le segment correspondant, et un 1 en sortie allume le segment correspondant. Montrer la table de vérité et une implémentation qui utilise uniquement un MUX (un MUX pour le segment d et un autre pour le segment g). Étiqueter chaque ligne du MUX par sa valeur.
Question 2
En utilisant la méthode Quine-McCluskey
sur la fonction boolénne : S(1,2,6,7,9,13,14,15,17,22,23,25,29,30,31)
- Donner tous les mintermes de la fonction
- Trouver tous ses implicants premiers
- Trouver tous ses implicants premiers essentiels
- Donner une couverture minimale de la fonction
- Simlifier la fonction S(1,2,6,7,9,13,14,15)en utilisant la méthode de Karnaugh
Question 3
Soit la machine à états finis suivante :
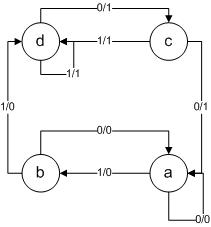
On décide de
coder les états en utilisant 2 bits
y0y1. Avec la correspondance suivante :
| État |
Codage
y0y1 |
| a |
11 |
| b |
10 |
| c |
00 |
| d |
01 |
- Il faudra établir la table de vérité de chaque sortie
ainsi que de chaque bit d'état.
- Il faudra aussi donner leur expression algébrique
sous forme simplifiée de somme de produits.
- Dessiner un circuit logique en utilisant des bascules
D ainsi que des portes logiques ET, OU, NON qui correspond à une réalisation
de la machine à états finis ci-haut.
- Dessiner un circuit logique en utilisant des bascules T ainsi que des portes logiques ET, OU, NON qui correspond à une réalisation de la machine à états finis ci-haut.