TPs 1 et 2 (Hiver 2004)
IFT3380/IFT6380
Par groupe de 2 étudiants
Première partie : à remettre jeudi 5 février à 23h59
Exercices 1.1, A1,
A5, A7 de H&P ed 3.
Deuxième partie : à remettre Jeudi 11 mars à 23h59 et Jeudi 18 mars
à 23h59
Exercices 1.3, 3.4,
3.6 de H&P ed 3. (Jeudi 11 mars à 23h59)
Exercice 4 :
(jeudi 18 mars à 23h59)
Théorie :
Toute fonction booléenne peut avoir une
représentation cubique, elle consiste en une table où chaque ligne est appelée
cube. Chaque cube correspond à un produit de la fonction dans la représentation
somme de produits
Ainsi la
fonction: ![]() possède la table
suivante :
possède la table
suivante :![]() .
.
0, 1, x
signifient respectivement : variable complémentée, non
complémentée ou absente du produit (don’t care).
Une
représentation interne utiliserait 2 bits pour chacune des trois valeurs: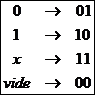
Ainsi la fonction
précédente serait représentée sur 8 bits : ![]()
Il s’agit
de trouver si un cube est inclus dans un autre dans une table et ainsi réduire
la table. On peut vérifier qu’un cube
est inclus dans un autre par l’opération intersection (qui consiste en un
ET logique) : ![]()
Ainsi si on
a :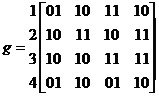 , on remarque que
, on remarque que ![]() donc peut être enlevé
donc peut être enlevé
On se
limite à des fonction d’au plus 16 variables, et on termine la table par le
cube 0…0 qui représente un cube vide.
Travail demandé :
Écrire en
assembleur MIPS, le programme qui lit une table et la simplifie.