Demo 2. Solutions.
1. Convertir -65 en notation IEEE-754 simple précision.
Solution:
65 = 10000012 = 1.000001 x 26
donc:
la partie fractionnaire .f est .0000 01
l'exposant e est 6
l'exposant biaisé ê est 127+6 = 128+5 =
1000 0000 + 0000 0101 = 1000 0101 en binaire
le bit de signe s est 1 (pour négatif)
La représentation s | ê | f est donc
s ê f
1 1000 0101 0000 0100 0000 0000 0000 000
On colle les bits et on les regroupe par 4
1100 0010 1000 0010 0000 0000 0000 0000
C 2 8 2 0 0 0 0
la reponse est donc C282 0000
b) 7.3125
Faut écrire en binaire:
7 est 111
.3125 x 2 = 0.6250
.625 x 2 = 1.25
.25 x 2 = 0.5
.5 x 2 = 1.0
et .3125 est donc .0101
7.4125 = 111.01012 = 1.1101 01 x 22
s = 0
ê = 127 +2 = 128 + 1 = 1000 0001
f = .1101 0100 0000 0000 0000 000
La prepresentation est
0 1000 0001 1101 0100 0000 0000 0000 000
qui en regroupant comme il faut par quartets (hexa) donne:
0100 0000 1110 1010 0000 0000 0000 0000
4 0 E A 0 0 0 0
Rep: 40EA 0000
2. Quel est le nombre dont la représentation IEEE simple précision est
8000 8000
Sol:
Il faut d'abord écrire les bits de ce nombre
1000 0000 0000 0000 1000 0000 0000 0000
puis les regrouper comme il faut pour retrouve s, ê et f
1 0000 0000 0000 0001 0000 0000 0000 000
Donc ê = 0 et le nombre est non normalisé
Le nombre est donc
- 0.0000 00012 x 2-126 = - 2-8 x 2-126
= - 2-134
Rep: (-1) x 2-134
3 Le plus petit nombre non nul normalisé:
Les nombres réels qui ont une représentation IEEE-754 normalisée exacte
sont de la forme:
(-1)s (1 + f)x 2e
avec f une fraction exprimable en binaire avec au plus 23 bits et
-126 <= e <= 127.
Le plus petit exposant possible pour le nombres normalisés est donc -126.
La plus petite fraction possible est 0.
Le plus petit nombre normalisé est donc 1.0 x 2-126 = 2-126
Les nombre reels qui ont une représentation IEEE-754 dénormalisée exacte
sont de la forme
(-1)s (0 + f) x 2-126
avec f une fraction exprimable en binaire avec au plus 23 bits.
Le plus petit f non nul exprimable avec 23 bits est (en binaire)
.0000 0000 0000 0000 0000 001
qui est en fait f = 2-23. Le plus petit nombre positif non
normalise est donc
(0 + 2-23) x 2-127 = 2-149
4
 5
5
 6
6
 7
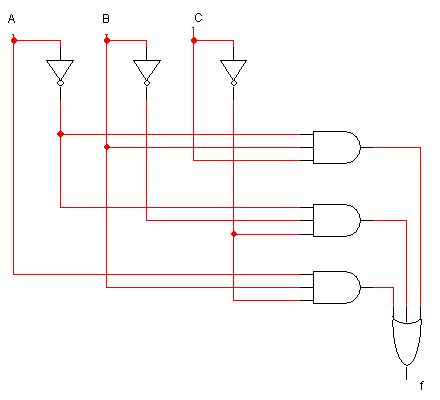
Pour montrer que les fonctions sont distinctes, suffit de trouver
des inputs qui donnent des sorties distinctes. Par exemple, pour A=0
B=1 et C=0 on a
f(A,B,C) = ABC + A'BC' = 0 + 1 = 1
g(A,B,C) = ( A XOR C)B (0 XOR 0) 1 = 0
Les fonctions sont donc distinctes. Pour trouver ces valeurs, on construit
la table de f et g et on arrete des qu'on a trouve une ligne ou f et g
different.
7
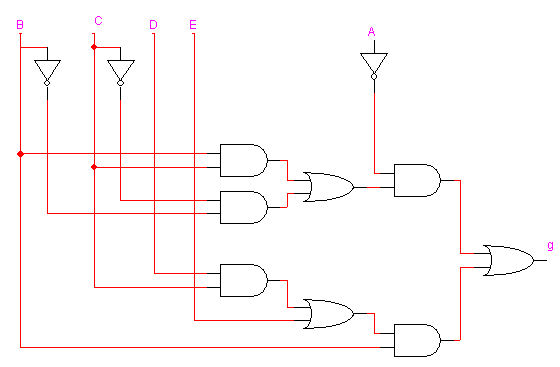
Pour montrer que les fonctions sont distinctes, suffit de trouver
des inputs qui donnent des sorties distinctes. Par exemple, pour A=0
B=1 et C=0 on a
f(A,B,C) = ABC + A'BC' = 0 + 1 = 1
g(A,B,C) = ( A XOR C)B (0 XOR 0) 1 = 0
Les fonctions sont donc distinctes. Pour trouver ces valeurs, on construit
la table de f et g et on arrete des qu'on a trouve une ligne ou f et g
different.
 5
5
 6
6
 7
Pour montrer que les fonctions sont distinctes, suffit de trouver
des inputs qui donnent des sorties distinctes. Par exemple, pour A=0
B=1 et C=0 on a
f(A,B,C) = ABC + A'BC' = 0 + 1 = 1
g(A,B,C) = ( A XOR C)B (0 XOR 0) 1 = 0
Les fonctions sont donc distinctes. Pour trouver ces valeurs, on construit
la table de f et g et on arrete des qu'on a trouve une ligne ou f et g
different.
7
Pour montrer que les fonctions sont distinctes, suffit de trouver
des inputs qui donnent des sorties distinctes. Par exemple, pour A=0
B=1 et C=0 on a
f(A,B,C) = ABC + A'BC' = 0 + 1 = 1
g(A,B,C) = ( A XOR C)B (0 XOR 0) 1 = 0
Les fonctions sont donc distinctes. Pour trouver ces valeurs, on construit
la table de f et g et on arrete des qu'on a trouve une ligne ou f et g
different.