Travaux pratiques IFT 1213, Hiver 2001
Démo 5Unité arithmétique entière. Flags.
| 1. | Calculez les flags V, N (Negatif, normalement appele bit de signe
et noté S ou FS sur pentium), C (carry), et Z (zero) pour les opérations
suivantes sur 8 bits
a) 10110101 - 01110101 b) 10101010 - 10000000 c) 01010101 - 10101010En regardant la table 6.6 p 287, dites pour a) b) et c) lequel des deux nombres est le plus grand en complément à deux. |
| 2. |
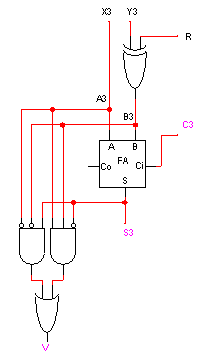 Dans le cas d'un additionneur/soustracteur (addition si R = 0, soustraction
si R = 1) on a construit le circuit ci-contre pour le calcul du bit
V de débordement (overflow OF) en complément à 2
(ici sur 4 bits).
Dans le cas d'un additionneur/soustracteur (addition si R = 0, soustraction
si R = 1) on a construit le circuit ci-contre pour le calcul du bit
V de débordement (overflow OF) en complément à 2
(ici sur 4 bits).
Pour effectuer la soustraction X - Y, le circuit calcule en fait la somme A + B + 1 avec 1 = c0, A = X et B = ~Y (négation bit à bit de Y). Montrer que dans le cas de la soustraction, V est 1 si et seulement si X est positif, Y négatif et S négatif ou si X est négatif, Y positif et S positif. |
| 3. | En classe on a vu comment implanter un additionneur-soustracteur
pour les nombres en représentation non signée et
complément à deux. Dans cet exercice, on vous demande de construire un additionneur-soustracteur pour les nombre en représentation "excès de 7" sur 4 bits. Ceci signifie que l'on code les nombres de -7 à 8 sur 4 bits de la facon suivante: -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 0 1 2 3 4 5 6 7 8 9 A B C D E FL'additionneur devra prendre en entree deux hex keyboard représentant les nombre X et Y en excès de 7, et un commutateur R. La sortie sera un "Hex display". Quand R=0, la sortie doit donner la somme de X et Y en "excès de 7", et quand R=1, la sortie doit être la representation de la différence. Par exemple si les entrées hexadécimales sont 8 (qui représente 1) et A (qui représente 3), et si R est 0 (somme), la sortie doit afficher B (qui représente la somme le 3 et 1, à savoir 4). |
| 4. | En utilisant des multiplexeurs 4 à 1, construisez un circuit
qui prend en entrée un nombre D de 4 bits
D3D2D1D0
et qui donne les sorties suivantes selon les bits de
sélection AB des multiplexeurs:
Bits AB Sortie 00 D 01 Multiplication de D par 2 10 Division non signée de D par 2 11 Division de D par 2 en complément à 2Par exemple, si l'input est 1100, alors on obtient les sorties suivantes: AB Sortie 00 1100 01 1000 (pas le choix, ici on perd un bit!) 10 0110 11 1110 |