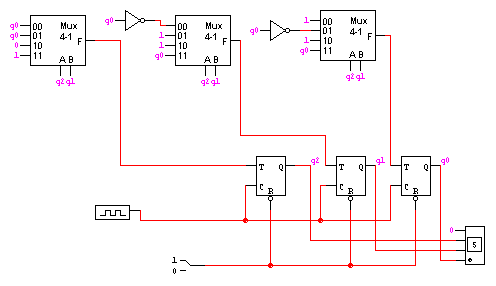
1. Compteur avec bascules T et MUX 4-1 pour la séquence 3,5,6,2,1,4,7,0. On a déjà fait en classe une solution avec bascules D et on trouve dans le répertoire ~dift1213/Circuits une solution avec bascules D et MUX 8-1. Voici le détail pour la solution avec bascules T et MUX 4-1: On code les états sur 3 bits, disons q2q1q0. L'Etat courant et le suivant sont donc deux suites de trois bits et les entrées des bascules T doivent satisfaire l'égalité:
t2t1t0 = Etat XOR Suivant
On construit la table qui pour chaque état donne son suivant puis
la valeur a donner en entrée à chaque bascule.
Etat q2q1q0 Suivant t2t1t0 0 000 3 011 011 1 001 4 100 101 2 010 1 001 011 3 011 5 101 110 4 100 7 111 011 5 101 6 110 011 6 110 2 010 100 7 111 0 000 111La table pour t2t1t0 peut donc se réecrire
q2 q1 t2 t1 t0 0 0 q0 not q0 1 0 1 q0 1 not q0 1 0 0 1 1 1 1 1 q0 q0Le circuit est donc:

2. Il suffit de conserver les bits dans trois registres de 1 bit (trois bascules D) qui forment un registre à décalage: disons que les trois derniers bits sont q2q1q0 (le dernier étant q0). Il suffit alors de se donner un circuit combinatoire suivant la table
q2 q1 q0 Z 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 0ce qui s'implante immediatement avec un MUX 8-1, presque immediatement avec un MUX 4-1, facilement avec PLA, ou directement avec des portes logiques. On a l'embarras du choix. Voici deux solutions
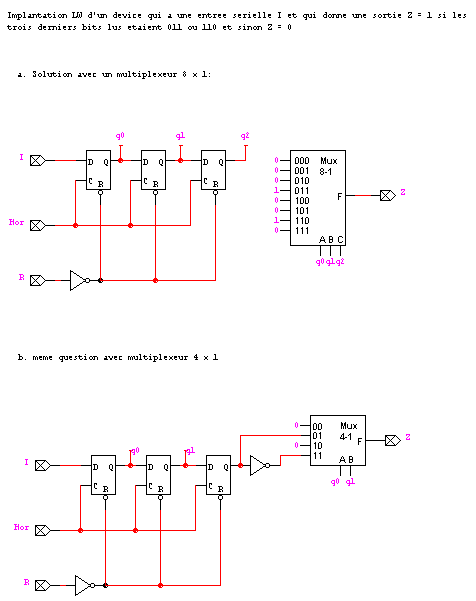
3.
R[3] <- R[4] + R[6] + 1Il faut 4 tranferts concrets; les voici avec les signaux associés.
| Transferts concrets | Signaux | Commentaire |
| W <- R[6] + 1 | R[6]out, Win; | Incrementation et copie dans W |
| Y <- W | Wout, Yin; | |
| Z <- R[4] + Y | R[4]out, Zin; | |
| R[3] <- Z | Zout, R[3]in; |
R[2] <- R[3] + R[4] + R[5]
| Transferts concrets | Signaux |
| Y <- R[5] | R[5]out, Yin; |
| Z <- R[4] + Y | R[4]out, Zin; |
| Y <- Z | Zout, Yin; |
| Z <- R[3] + Y | R[3]out, Zin; |
| R[2] <- Z | Zout, R[2]in; |
4. Dans le circuit de la figure 2.23, page 80, suffit de remplacer R[1] par A, R[2] par B, W par C, de garder l'incrementeur tel quel et d'enlever l'additionneur et les autre registres. Chacun des transferts abstraits de la question devient un transfert concret produit par les signaux suivants
| Transfert | Signaux |
| A <- B | Aout, Bin; |
| C <- B + 1 | Bout, Cin; |
| A <- C | Cout, Ain; |
| B <- C | Cout, Bin; |