|
PLearn 0.1
|
|
PLearn 0.1
|
#include "pl_math.h"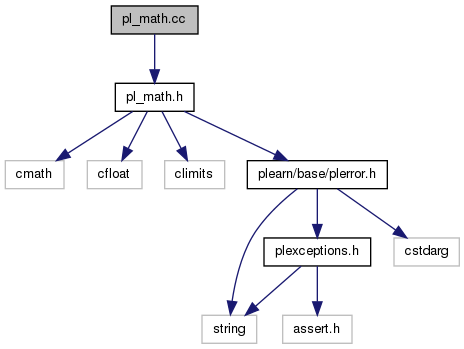
Go to the source code of this file.
Namespaces | |
| namespace | PLearn |
< for swap | |
Functions | |
| bool | PLearn::is_equal (real a, real b, real absolute_tolerance_threshold=1.0, real absolute_tolerance=ABSOLUTE_TOLERANCE, real relative_tolerance=RELATIVE_TOLERANCE) |
| Test float equality (correctly deals with 'nan' and 'inf' values). | |
| real | PLearn::safeflog (real a) |
| real | PLearn::safeexp (real a) |
| real | PLearn::log (real base, real a) |
| real | PLearn::logtwo (real a) |
| real | PLearn::safeflog (real base, real a) |
| real | PLearn::safeflog2 (real a) |
| real | PLearn::tabulated_softplus_primitive (real x) |
| real | PLearn::logadd (double log_a, double log_b) |
| compute log(exp(log_a)+exp(log_b)) without losing too much precision (doing the computation in double precision) | |
| real | PLearn::square_f (real x) |
| real | PLearn::logsub (real log_a, real log_b) |
| compute log(exp(log_a)-exp(log_b)) without losing too much precision | |
| real | PLearn::small_dilogarithm (real x) |
| real | PLearn::positive_dilogarithm (real x) |
| real | PLearn::dilogarithm (real x) |
| It is also useful because -dilogarithm(-exp(x)) is the primitive of the softplus function log(1+exp(x)). | |
| real | PLearn::hard_slope_integral (real l, real r, real a, real b) |
| real | PLearn::soft_slope_integral (real smoothness, real left, real right, real a, real b) |
| real | PLearn::tabulated_soft_slope_integral (real smoothness, real left, real right, real a, real b) |
Variables | |
| float | PLearn::tanhtable [TANHTABLESIZE] |
| PLMathInitializer | PLearn::pl_math_initializer |
Definition in file pl_math.cc.
 1.7.4
1.7.4