Clustering et classification des documents (sommaire)
1. But de Clustering
-Le nombre de clusters, par rapport au nombre de documents, est beaucoup plus petit. Ainsi, on peut accélérer le processus de recherche.
-Si on document est pertinent à une requête, alors les documents similaires ont plus de chance à être pertinents aussi. Ainsi, les clustering peut être aussi vu comme un moyen d'expansion.
-Finalement, les réponses du système peut être regroupées, plutôt qu'être mises dans une liste individuellement. L'avantage de cette présentation de résultats est que l'utilisateur peut avoir une idée globale des résultats que le systèmes a trouvés assez rapidement.
Avec le progrès rapide sur les matériels d'informatique, le premier avantage semble beaucoup moins important maintenant. Les deux autres restent toujours d'actualité.
2. Méthodes de clustering
-Hiérarchique
-non-hiérarchique
Le premier type d'algorithme essaie de créer une hiérarchie des clusters, les documents les plus similaires sont regroupés dans des clusters au plus bas niveaux, tandis que les document moins similaires sont regroupés dans des clusters aux plus haut niveaux.
Selon comment la hiérarchie est créée, ce type d'algorithmes peut encore se diviser en deux: divisif ou agglomératif. En partition, on tente de diviser un grand cluster en 2 plus petits (approche descendante). En regroupement, on tente de regrouper 2 clusters en un plus grand (approche ascendante).
Le deuxième type d'algorithmes ne crée pas une hiérarchie. Les clusters sont au même niveau.
Parmi les algorithmes souvent utilisés, il y a:
k-means:
1.choisir k germes (seeds)
2.attacher les points aux clusters dont le centroïde est le plus proche
3.re-calculer le centroïde
4.répéter jusqu'à ce que les centroïdes se stabilisent.
k-Nearest-Neighbors (kNN): Dans cet algorithme, un point est d’abord associé à k points voisins les plus proches. Le cluster auquel est associé le plus grand nombre de voisins est le cluster choisi.
Agglomératif:
1.calculer la similarité entre les clusters (au début, chaque document forme un cluster tout seul)
2.regrouper les 2 clusters les plus similaires
3.répéter 1-2 jusqu'à obtenir un seul cluster
bisection
k-means:
1.déterminer un cluster pour couper en 2
2.couper ce cluster en deux clusters
3.répéter l'étape 2 ITER fois et prendre les clusters coupés dont la similarité globale au sein de ces clusters est la plus élevée
4.répéter 1-3 jusqu'à obtenir k clusters
3. Mesures
Similarité de clusters: elle est définie comme la similarité
-entre les centroïdes de ces clusters (le centroïde est le vecteur moyen de tous les éléments dans le cluster)
-ou bien entre les medoïdes de ces clusters (le medoïde est l'élément le plus au centre du cluster)
Quelques variantes:
Sim(C1, C2) = åd1ÎC1, d2ÎC2 cos(d1,d2) / (taille(C1)*taille(C2))(UPGMA)
Sim(C1, C2) = Similarité entre deux éléments les plus proches des deux cluatsres
Il y a aussi des algorithmes qui utilisent la similarité d'un élément avec tous les éléments du cluster comme critère, ou bien une mesure de cohésion de cluster.
Références
sur clustering
http://www-users.cs.umn.edu/~karypis/publications/Papers/PDF/doccluster.pdf (à lire pour clustering hiérarchique et une comparaison)
http://www.clustan.com/k-means_critique.html (Une analyse sur k-means)
http://www.engr.sjsu.edu/~knapp/HCIRDFSC/C/C_home.htm (à lire pour k-means)
http://www-4.ibm.com/software/data/iminer/fortext/tatools.html
(IBM text processing tools)
http://www-users.cs.umn.edu/~boley/
(Clustering)
http://www-users.cs.umn.edu/~karypis/
(Clustering)
http://www.ima.umn.edu/talks/workshops/4-17-18.2000/index.html
(IMA workshop on text mining)
http://www.cs.cmu.edu/afs/cs/project/theo-4/text-learning/www/
(CMU text learning group)
http://www-personal.umich.edu/~wfan/text_mining.htmlText
Mining, Web
Mining, Information Retrieval and Extraction from the WWW References
http://www.research.microsoft.com/research/db/debull/A00sept/issue.htm
(IEEE Data Engineering Bultin, special issue on Next generation Web
search)
http://astro.u-strasbg.fr/~fmurtagh/mda-sw/online-sw.html
(Online clustering software references)
http://www.pitt.edu/~csna/software.html
(On-Line Software for Clustering and Multivariate Analysis)
http://search.sify.com/Top/Reference/Knowledge_Management/Knowledge_Discovery/Text_Mining/
(Reference list of text mining software and projects, also a list for
log-analysis)
http://lifestyleopportunity.org/index/Computers/Software/Databases/Data_Mining/
(Reference list of text mining software and projects, also a list for
log-analysis)
http://databases.about.com/compute/databases/gi/dynamic/offsite.htm?site=http://www.statsoft.com/textbook/stathome.html
(Online book for statistical analysis, including a chap. on
classification
tree)
http://databases.about.com/compute/databases/cs/datamining/(references
and introductions to text mining)
http://directory.google.com/Top/Reference/Knowledge_Management/Knowledge_Discovery/Text_Mining/
(Google references on text mining)
Comme un article facile à comprendre, je vous suggère un qui se trouve à:
http://www-users.cs.umn.edu/~karypis/publications/data-mining.html
SKK00a
A Comparison of Document Clustering Techniques
Michael Steinbach, George Karypis and Vipin Kumar
TextMining Workshop, KDD, 2000
Une autre liste de référence commentée très intéressante sur clustering (provient de Berkeley?)
5. Problème de la classification
Pour pouvoir classer le document, il est nécessaire de comparer le contenu de ce document avecla description de chaque classe, et de déterminer la ou les classes les plus semblables. La première tâche dans la classification est donc de créer une description pour chaque classe.
Il est possible que chaque classe possède déjà une description sommaire. Par exemple, nous pouvons avoir une classe « sport » qui est décrite par les mots clés suivants : football, basketball, tennis, hokey, … Cette description peut constituer une description de la classe. Cependant, dans beaucoup de cas en pratique, une telle description n’est pas disponible. Même si elle est disponible, cette description n’est souvent pas exhaustive, ni assez précise. Ainsi, on a besoin d’autres moyens pour créer ou pour enrichir cette description.
L’approche en général est celle par l’entraînement avec un ensemble d’exemples classés. Pour chaque classe, nous avons un ensemble de documents que nous avons jugés manuellement comme faisant partie de la classe. Ces document constituent des exemple d’entraînement pour cette classe. La tâche de classification est :
- d’extraire une description de la classe (ou garder les exemples séparément, comme dans l’algorithme kNN)
- définir un algorithme permettant de déterminer la ou les classes les plus appropriées pour un document á classer.
Ces deux sous-tâches sont fortement reliés, et traités ensemble. Dans la prochaine section, on décrit un ensemble d’algorithme de classifications classiques.
6. Algorithmes
6.1. Roccio
Q’ = a*Q + b*P - g*NP
où Q’ est la nouvelle requête, Q est l’ancienne, P est le vecteur centroïde des documents jugés pertinents, et NP le centroïde des documents jugés non-pertinents, et a, b et g sont des paramètres à fixer de façon expérimentale.
Pour la classification, on doit aussi construire deux centroïdes P et N pour chaque classe Ci . Supposons que la classe Ci contient l’ensemble Ei d’exemples, et les autres exemple à l’extérieur de Ci est NEi. Les centroïdes P et NP sont construits à partir de ces deux ensembles. Ainsi, la description pour la classe Ci est comme suit :
Ci
= b*P
- g*NP
Pour vous donner une idée sur les valeurs de b et g utilisées, dans une expérimentation, b=16 etg=4.
6.2. kNN (k-Nearest-Neighbors)
![]()
où sim(Dj,D) est la similarité entre le document exemple Dj et le nouveau document D, C(Dj) est la classe du document Dj, d(.,.) est la fonction Kroneker qui est 1 si les deux arguments sont identiques, et 0 sinon. On choisit la classe Ci dont le vote pour elle est le plus fort (noté par arg maxi).
6.3. Naïve Bayes
P(Ci|D)
La classe Ci qui donne la probabilité la plus forte est choisie.
Cependant, cette probabilité n’est pas directement estimable. Ainsi, on utilise la loi de Bayes :
P(Ci|D) = P(D|Ci) P(Ci) / P(D) µ P(D|Ci) P(Ci)
Pour P(Ci), nous pouvons l’estimer par #exemples_dans_Ci / #exemples
Comme dans le modèle probabiliste, on suppose que le document D est décrit par un ensemble de présences et d’absences des termes. Notons chaque présence par tj=xj (où xj=1 signifie que le terme tj est présent, et xj=0 signifie qu’il est absent).
Ensuite, supposons aussi indépendance entre les termes. Nous avons donc :
P(D|Ci) = ÕxjÎD P(xj|Ci)
Pour l’estimation de P(xj|Ci), on utilise le même principe que dans le modèle probabiliste indépendant.
6.4. Arbre de décision
Le problème clé en est un de construction de l’arbre à partir d’un ensemble d’exemples. Il existe des algorithme de construction connus, par exemple ID3 et C4.5. Ces algorithmes tentent de choisir un attribut le plus « discriminatif » permettant de séparer un ensemble de cas exemples en des sous-ensembles les plus homogènes possibles. Cette décision se fait en utilisant la notion de gain d’information, issue de la théorie de l’information.
Rappelons que la quantité de l’information peut être mesurée par l’entropie définie comme suit :
![]()
où M est un message composé d’un ensemble de mi, et p(mi) est la probabilité de mi.
Soit les deux arbres suivants :
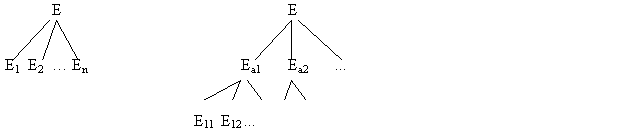 où
E est l’ensemble des exemples données (déjà
classés).
E1, E2,… sont des exemples classés dans la
classe C1,C2, … Ea1, Ea2,
…
sont des sous-ensembles d’exemples séparés selon la
valeur
d’un attribut a, et E11, E12, … sont des
sous-ensembles
de Ea1 dans chaque classe C1, C2, …
où
E est l’ensemble des exemples données (déjà
classés).
E1, E2,… sont des exemples classés dans la
classe C1,C2, … Ea1, Ea2,
…
sont des sous-ensembles d’exemples séparés selon la
valeur
d’un attribut a, et E11, E12, … sont des
sous-ensembles
de Ea1 dans chaque classe C1, C2, …
Le gain d’information d’un attribut est déterminé par la différence de la quantité d’information du deuxième arbre par rapport à la quantité d’information du premier arbre. Ces deux quantités sont calculées comme suit :
![]()
où p(Ei) = |Ei| / |E|
![]()
Le gain d’information pour l’attribut a est donc I(arbre2) – I(arbre1). Cette différence mesure la valeur qu’apporte l’attribut a.
Pour la construction de l’arbre, on choisit à utiliser d’abord l’attribut dont le gain d’information est le plus grand. Une fois l’ensemble de tous les exemples est séparé en plusieurs sous-ensemble, on réutilise la même stratégie pour continuer à séparer ces sous-ensemble, jusqu’à obtenir des sous-ensembles homogènes (correspondant à une seule classe).
6.5. Support vector machine (SVM)
Une fois un tel hyperplan est déterminer pour chaque classe, il peut être utilisé pour déterminer si un nouveau document peut être classé dans cette classe ou non.
7. Problème de dimensionnalité (feature selection and feature extraction)
Pour éliminer encore plus de dimensions bruits, on peut
-choisir les dimensions dont la fréquence d’occurrence (tf) est parmi les plus fortes pour une classe
-choisir celles dont la valeur de tf*idf est parmi les plus forts pour une classe
-déterminer une valeur de discrimination d’un index . Cette valeur reflète le pouvoir de cet indexe de distinguer la classe des autres classes. Le poids idf en est un exemple.
A part cette sélection, il y a aussi des méthodes qui extraient des caractéristiques à partir des dimensions originales. LSI en est un exemple. En utilisant LSI, les dimensions originales sont converties (en se regroupant) en un ensemble d’autres dimensions par la décomposition de valeur singulière. Les dimensions les plus fortes sont gardées, tandis que les dimensions faibles sont considérées comme des bruits, et sont éliminées. Cette méthode permet aussi d’obtenir un nombre restreint de dimensions.
Références
Dans cette longue liste, je vous suggère particulièrement les "surveys" suivants:
Kjersti Aas, Line Eikvil, Text Categorisation: A Survey. http://citeseer.nj.nec.com/aas99text.html
Fabrizio Sebastiani, A Tutorial on Automated Text Categorisation (1999)http://citeseer.nj.nec.com/sebastiani99tutorial.html
Deux travaux représentatifs dans la communauté de RI sont:
Yang,
Y. (1999). An evaluation of statistical approaches to text
categorization.
Journal of Information Retrieval, 1999, http://citeseer.nj.nec.com/yang97evaluation.html
David
D. Lewis and William A. Gale, A sequential algorithm for training text
classifiers, Proceedings of SIGIR-94, 17th ACM International Conference
on Research and Development in Information Retrieval, Springer Verlag,
Heidelberg, DE, Dublin, 3--12, 1994, http://citeseer.nj.nec.com/lewis95sequential.html
ou http://www.research.att.com/~lewis/papers/lewis94c.ps
Questions à réfléchir sur
la classification :
- De façon intuitive, quelles méthodes vous sembles les plus raisonnables ? Pour avoir une intuition sur la classification, faites l’exercice de classer quelques articles de journaux, et observez les critères que vous utilisez dans cette tâche.
- Est-ce que les approches intuitives ont donnés de bons résultats dans les expérimentations décrites dans les références ? Sinon, est-ce que vous pouvez trouver une explication ?
- A votre avis, quels sont les problèmes posés à chacune des étapes de la classification, et lesquels sont les plus importants ?
- Indexation des documents exemples et le nouveau document
- Sélection des caractéristiques à utiliser
- Algorithme de classification
- Qu’est-ce qu’on doit faire si on enrichit les classes en ajoutant de nouvelles classes ?
- Qu’arrive-t-il si aucun exemple n’est disponible pour une classe ? Et si le nombre d’exemples ne sont pas équilibré ?
- Que signifie « overfitting » ? Dans quelle situation ce phénomène arrive ? Comment faire pour l’éviter ?
- Quelles sont les danger d’utiliser un arbre de décisions pour la classification ? Quelles modifications doit-on apporter sur la méthode de base décrite en haut ?
- Pourquoi SVM a souvent donné de bonne performance dans les expérimentations ? Avez-vous une explication ?
- A-t-il d’autre façon de déterminer les caractéristiques les plus utiles pour la classification ?
- Quels sont les problèmes dans la méthode de Naïve Bayes ?