Modèles de recherche d'information
Si c'est l'indexation qui choisit les termes pour représenter le contenu d'un document ou d'une requête, c'est au modèle de leur donner une interprétation. Étant donné un ensemble de termes pondérés issus de l'indexation, le modèle remplit les deux rôles suivants:
Le modèle joue un rôle central dans la RI. C'est le modèle qui détermine le comportement clé d'un système de RI. Dans ce chapitre, on décrit quelques modèles souvent utilisés dans la RI. Quelques modèles plus récents seront décrits plus tard dans la deuxième partie (élargissement) du cours. Dans la présentation qui suit, pour chaque modèle, on décrira les deux aspects clés: la représentation et la comparaison.
1. Modèle "Matching score"
C'est peut-être le premier "modèle" utilisé dans la RI. L'idée est assez primitive et intuitive: Un document est représenté par un ensemble de termes pondérés par leur fréquence. Une requête est aussi un ensemble de termes, pondérés à 1. Le degré de correspondance est la somme des fréquences des termes de la requête dans le document:
R(d, q) = S i fi
où fi est la fréquence d'un terme de q dans le document d.
La valeur R ainsi calculée est appelée la "matching score". En réalité, cela est équivalent à parcourir le document, et de voir combien de fois les termes de la requête apparaissent dans ce document. Plus ce matching score est élevé, plus on considère que le document correspond à la requête, et donc plus il sera classé haut dans la réponse.
Ce modèle est primitif car il utilise directement le résultat de l'indexation sans aucune réorganisation ou modélisation.
2. Modèle booléen
Dans ce modèle, un document est représenté comme une conjonction logique de termes (non pondérés), par exemple,
d = t1 Ù t2 Ù Ù tn
Une requête est une expression logique quelconque de termes. On peut utiliser les opérateur et (Ù ), ou (Ú ) et non (Ø ). Par exemple:
q = (t1 Ù t2) Ú (t3 Ù Ø t4)
Pour qu'un document corresponde à une requête, il faut que l'implication suivante soit valide:
d Þ q.
Cette évaluation peut être aussi définie de la façon suivante:
Un document est représenté comme un ensemble de termes, et une requête comme une expression logique de termes. La correspondance R(d, q) entre une requête et un document est déterminée de la façon suivante:
R(d, ti) = 1 si ti Î d; 0 sinon.
R(d, q1 Ù q2) = 1 si R(d, q1) = 1 et R(d, q2) = 1; 0 sinon.
R(d, q1 Ú q2) = 1 si R(d, q1) = 1 ou R(d, q2) = 1; 0 sinon.
R(d, Ø q1) = 1 si R(d, q1) = 0; 0 sinon.
On peut remarquer deux problèmes dans ce modèles
Il faut cependant remarquer que ce modèle booléen standard n'est utilisé que dans très peu de systèmes de nos jours. Si on utilise un modèle booléen, c'est plutôt une extension de ce modèle qu'on utilise. Les extensions proposées essaient justement de corriger ces lacunes.
3. Modèle Booléen basé sur des ensembles flous
Cette extension au modèle booléen standard vise à tenir compte de la pondération des termes dans les documents. Du côté requête, elle reste toujours une expression booléenne classique.
Avec cette extension, un document est représenté comme un ensemble de termes pondérés comme suit:
d = { , (ti, ai), }
L'évaluation d'une requête peut prendre plusieurs formes. Une d'elles est la suivante:
R(d, ti) = ai
R(d, q1 Ù q2) = min(R(d, q1), R(d, q2)).
R(d, q1 Ú q2) = max(R(d, q1), R(d, q2)).
R(d, Ø q1) = 1 - R(d, q1).
Dans cette évaluation, les opérateurs logiques Ù et Ú sont évalués par min et max respectivement. C'est une des évaluations classiques proposées par L. Zadeh dans le cadre des ensembles flous. Cependant, cette évaluation n'est pas parfaite. Par exemple, on n'a pas R(d, qÙ Ø q) º 0 et R(d, qÚ Ø q) º 1. Du point de vue théorique, c'est gênant. Du point de vue pratique, quand on évalue une requête en forme de conjonction, on ne s'intéresse qu'à la partie la plus difficile, et quand on évalue une requête en forme de disjonction, c'est la partie la plus facile qui domine. Intuitivement, on aimerait plutôt que les deux parties jouent toutes les deux un rôle dans l'évaluation. Ainsi, beaucoup d'autres formes dévaluation ont été proposées. Une des formes est l'évaluation Lukaswicz qui est la suivante:
R(d, ti) = ai
R(d, q1 Ù q2) = R(d, q1) * R(d, q2).
R(d, q1 Ú q2) = R(d, q1) + R(d, q2) - R(d, q1) * R(d, q2).
R(d, Ø q1) = 1 - R(d, q1).
Dans cette évaluation, on voit que les deux parties d'une conjonction ou d'une disjonction contribuent en même temps, contrairement à celle de Zadeh. Cependant, elle a le même problème qui est R(d, qÙ Ø q) ¹ 0 et R(d, qÚ Ø q) ¹ 1. En plus, R(d, qÙ q) ¹ R(d, q) ¹ R(d, qÚ q).
Si on compare ces extensions avec le modèle standard, il est assez facile de voir les avantages. Le plus important est qu'on peut mesurer le degré de correspondance entre un document et une requête dans [0, 1]. Ainsi, on peut ordonner les documents dans l'ordre décroissant de leur correspondance avec la requête. L'usager peut parcourir cette liste ordonnée et décider où s'arrêter. Au niveau de la représentation, on a également une représentation plus raffinée. On peut exprimer dans quelle mesure un terme est important dans un document.
Ces évaluations ont été proposées à la fin des années 1970 et au début des années 1980. Maintenant, ces extensions sont devenues standard: la plupart des systèmes booléens utilisent un des ces modèles étendus.
Reformulation de la requête
Il a été observé qu'une requête qui est une longue conjonction est très difficile à satisfaire. Dans bien des cas, la réponse est vide. Dans l'autre extrême, une longue disjonction est très facile à satisfaire. On aura alors beaucoup de documents en réponse. C'est surtout pour résoudre le premier problème qu'on veut reformuler la requête initiale.
Dans le cas d'une longue requête en conjonction, si un document satisfait la plupart des termes de la requête, on peut penser qu'il satisfait en partie le besoin de l'usager. Au lieu de donner aucune réponse à l'usager, il vaut mieux de donner un ensemble de documents partiellement satisfaisants. Ainsi, le processus de reformulation consiste à examiner le nombre de documentrs en réponse. S'il est très peu, alors on peut assouplir la requête initiale en supprimant un terme. Par exemple, soit une requête initial q = t1 Ù t2 Ù t3 Ù t10. Si aucun document n'a été trouvé pour cette requête, on peut l'assouplir en la suivante:
q' = (t2 Ù t3 Ù t4 Ù ... t10) Ú
(t1 Ù t3 Ù t4 Ù ... t10) Ú
...
(t1 Ù t2 Ù t3 Ù t9)
Cette reformulation peut continuer si nécessaire.
Cette façon n'est pas unique. Une autre façon possible de reformuler consiste à supprimer le terme qui est le plus difficile à satisfaire (celui qui correspond au moins de documents). On peut en imaginer encore d'autres. En effet, ces assouplissements sont justifiées seulement par des besoins pratiques. Elles n'ont pas besoin de justification théorique.
Associer une importance aux termes de la requête
Certains auteurs suggèrent d'associer une importance à chaque terme de la requête pour que l'usager puise différencier des termes très importants de ceux qui le sont moins. On peut voir certaines propositions dans les articles de Waller, Kraft et Redecki.
Cependant, ces propositions n'ont jamais gagné du terrain dans la pratique. La raison principale est qu'il est difficile de comprendre le sens de la pondération associée à un terme. Par exemple, pour une expression comme (t, b) dans une requête, on peut comprendre que b est un seuil, b est un facteur de multiplication (i.e. son évaluation est celle de t multipliée par b), ou un facteur de division. Il n'y a jamais eu de consensus là-dessus. On a mentionné qu'il est déjà difficile pour un usager moyen d'utiliser correctement les opérateurs logiques. Il est impensable qu'ils puissent mettre une pondération correcte en plus.
4. Modèle vectoriel
C'est un autre modèle souvent utilisé. Dans ce modèle, un document, ainsi qu'une requête, est représenté comme un vecteur de poids. Chaque poids dans le vecteur désigne l'importance d'un terme correspondant dans ce document ou dans la requête. Pour qu'un vecteur prennent une signification, il faut d'abord définir un espace vectoriel. L'espace vectoriel est définit par l'ensemble de termes que le système a rencontré durant l'indexation. Soit l'espace vectoriel suivant:
<t1, t2, t3, , tn>
un document et une requête peut être représenté comme suit:
d = < a1, a2, a3, , an>
q = < b1, b2, b3, , bn>
où pi et qi correspondent aux poids du terme ti dans le document et dans la requête.
Étant donné ces deux vecteurs, leur degré de correspondance est déterminée par leur similarité.
Il y a plusieurs façon de calculer la similarité entre deux vecteurs. En voici quelques unes:
Sim0(d, q) = S i (ai * bi) (produit interne)
Sim1(d, q) = S i (ai * bi) / [S i (ai)2 * [S i (bi)2]1/2 (cosinus)
Sim2(d, q) = 2 S i (ai * bi) / [[S i (ai)2 + [S i (bi)2]
Sim3(d, q) = S i (ai * bi) / [[S i (ai)2 + [S i (bi)2 - S i (ai * bi)]
Sauf la première formule, toutes les autres sont normalisées, c'est-à-dire qu'elles donnent une valeur dans [0, 1].
Vous pouvez vous poser la question suivante: étant donné un grand nombre de termes dans l'espace vectoriel, l'évaluation peut prendre beaucoup de temps car on doit examiner chaque terme, et ce pour chaque document. Est-ce que le temps de réponse du système va être exorbitant? La réponse est non. On n'a pas besoin de comparer chaque document individuellement avec la requête comme exprimé dans ces formules. On peut très bien le faire pour l'ensemble de documents dans la base de documents. L'idée est d'utiliser un fichier inversé. Un fichier inversé donne, pour chaque terme, l'ensemble de documents qui le contiennent et le poids. Ainsi, pour chaque terme de la requête, on peut connaître, par une seule consultation de ce fichier, l'ensemble de documents concernés. On fera cela pour tous les termes de la requête (qui sont peu nombreux), et cela restreint naturellement l'évaluation à un sous-ensemble de documents dans la base. Le reste du travail consiste à combiner ces ensembles de documents et de calculer le poids. On verra cela plus en détail plus tard dans l'implantation des modèles.
Remarquez également que certaines formules peut être transformée en un produit interne si on manipule les poids d'une certaine façon. Le cas typique est pour la formule cosinus. Cette formule peut être transformée comme suit:
Sim1(d, q) = S i [(ai / [S j (aj)2]1/2) * (bi / [S j (bj)2]1/2)]
Dans cette formule, on a deux éléments clairement séparés: ai / [S j (aj)2]1/2 et bi / [S j (bj)2]1/2. En réalité, l'ajout des dénominateurs consiste à normaliser le poids initial ai et bi. Remarquez en plus que cette normalisation peut être faire indépendamment: dans le cas de document, la normalisation n'utilise que les termes du document, et la même chose pour la requête. Ainsi, il est possible de calculer deux autres poids ai' = [(ai / [S j (aj)2]1/2) et bi' = (bi / [S j (bj)2]1/2) au préalable et de remplacer les poids dans les vecteurs. Si on fait cela, le calcule de similarité selon la formule de cosinus sera juste un produit interne: Sim1(d, q) = S i (ai' * bi' ). Ainsi, le temps d'évaluation peut être raccourci. Cette approche est prise dans le système SMART (qui sera décrit plus tard).
5. Modèle p-norme
Le modèle p-norme [Salton, Fox et Wu, 83] est proposé pour résoudre certains problèmes observés dans le modèle booléen standard:
L'approche proposée tente d'étendre le modèle booléen standard sur plusieurs aspects. D'abord, observons la table de vérité utilisée pour l'évaluation booléen standard:
|
A |
B |
A Ù B |
A Ú B |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
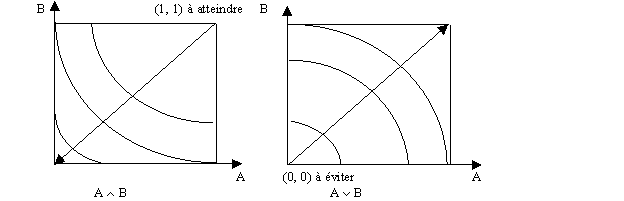
Dans la colonne de A Ù B, l'objectif est d'atteindre le cas de la dernière ligne. Dans la colonne de A Ú B, c'est plutôt la première ligne qu'il faut éviter. Ainsi, une façon de floufier (fuzzify) l'évaluation stricte consiste à calculer une sorte de distance entre le points à éviter ou à atteindre. Selon cette distance, on va déterminer l'évaluation de la conjonction ou de la disjonction. L'idée de base correspond aux figures suivantes:

Dans ces figures, étant donné une évaluation de A et de B, on détermine un point dans l'espace A-B. Dans la première figure, on cherche à évaluer dans quelle mesure ce point est proche de (1, 1) - le point à atteindre. Ce rapprochement peut être mesurée par le complément de la distance entre le point et le point (1, 1): plus cette distance est grande, moins A Ù B est satisfaite à ce point. Pour les points qui se situent sur une même courbe, ils ont la même distance avec (1, 1). Dans le cas de A Ú B, on cherche plutôt à éviter le point (0, 0). Plus on est loin de (1, 0), plus A Ú B est satisfaite.
Basée sur cette intuition, l'évaluation suivante est proposée. On admet la pondération de termes dans les documents: pi est le poids de ti dans d.
R(d, ti) = pi
R(d, q1 Ù q2) = 1 - ([(1-R(d, q1))2 + (1-R(d, q2))2] / 2)1/2.
R(d, q1 Ú q2) = [(R(d, q1)2 + R(d, q2)2) / 2]1/2.
R(d, Ø q1) = 1 - R(d, q1).
Dans cette évaluation, la distance est normalisée (divisée par 21/2).
Généralisation 1
Une première généralisation de l'évaluation précédente consiste à permettre aussi à associer une pondération aux termes de la requête. Dans cette approche, la signification de cette pondération est bien définie: elle mesure l'importance du terme pour le besoin de l'usager. Plus un terme a une pondération forte, plus il est important. Ainsi, une requête prend la forme suivante:
q = t1b1 Ù (t2b2 Ú t3b3)
L'évaluation devient la suivante (supposons que ai est le poids de ti dans d):
R(d, ti bi) = ai * bi
R(d, q1 b1 Ù q2 b2) = 1 - [[b12 * (1-R(d, q1))2 + b22 * (1-R(d, q2))2] / (b12 + b22)]1/2.
R(d, q1 b1 Ú q2 b2) = [b12 * (R(d, q1)2 + b22 * R(d, q2)2) / (b12 + b22)]1/2.
R(d, Ø q1) = 1 - R(d, q1).
Généralisation 2
On peut également vouloir attribuer une pondération aux opérateurs logiques pour déterminer dans quelle mesure un opérateur doit être évaluée de façon stricte. C'est le rôle du facteur p qu'on ajoute sur un opérateur. Les opérateurs Ù p et Ú p sont évalués comme suit:
R(d, q1 b1 Ù p q2 b2) = 1 - [[b1p * (1-R(d, q1))p + b2p * (1-R(d, q2))p] / (b1p + b2p)]1/p.
R(d, q1 b1 Ú p q2 b2) = [b1p * (R(d, q1)p + b2p * R(d, q2)p) / (b1p + b2p)]1/p.
Cela correspond à remplacer une distance euclidienne par une distance "p_norme". La valeur de p peut varier dans [1, ∞). Plus p est grand, plus l'évaluation est stricte. Cela peut se comprendre par l'examen de deux cas extrêmes: quand p=1, on retrouve une évaluation équivalente à celle du modèle vectoriel; quand p→∞, l'évaluation est équivalente à celle du modèle booléen standard ou basée sur des ensembles flous. On ne donne pas de preuve ici, mais il est assez facile de prouver les suivants:
R(d, q1 b1 Ù 1 q2 b2) = [b1 * R(d, q1) + b2 * R(d, q2)] / (b1 + b2).
R(d, q1 b1 Ú 1 q2 b2) = [b1 * R(d, q1) + b2 * R(d, q2)] / (b1 + b2).
La conjonction et la disjonction deviennent identiques. Cette évaluation correspond à sim0 du modèle vectoriel.
R(d, q1 b1 Ù ∞ q2 b2) = min(R(d, q1), R(d, q2)).
R(d, q1 b1 Ú ∞ q2 b2) = max(R(d, q1), R(d, q2)).
Cette évaluation est la même que celle du modèle basée sur des ensembles flous.
Basé sur cette comparaison, on peut donc voir que le comportement du modèle p-norme varie entre le modèle booléen et le modèle vectoriel comme illustré dans la figure suivante:
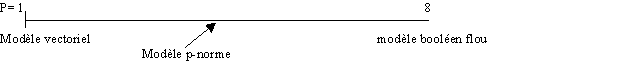
Le modèle p-norme est intéressant non pas pour sa performance en pratique (bien que les expérimentations montrent qu'il est meilleur que le modèle vectoriel et le modèle booléen séparé), mais pour son cadre unificateur. Cela nous aide à comprendre la différence entre le modèle vectoriel et le modèle booléen: un modèle vectoriel peut être considéré comme un modèle booléen dans lequel la différence entre la conjonction et la disjonction est effacée; ou bien la relation entre deux termes dans un vecteur est une relation et-ou neutre. C'est la seule relation qu'on peut exprimer dans le modèle vectoriel.
6. Quelques mots sur l'implantation des modèles
Nous avons déjà mentionné qu'il existe des méthodes plus efficace pour évaluer une requête, que de la comparer à chaque document individuellement. La clé de ces approches est l'utilisation d'un fichier inversé.
Le résultat d'une indexation donne un ensemble de termes et leurs pondérations pour chaque document comme suit:
dj ® { , (ti, aij), }
Avec ce résultat, il est facile à trouver les termes inclus dans un document. Cependant, étant donné une requête qui contient quelques termes, on est plus intéressé à retrouver les documents correspondant à chacun de ces termes. Donc, on veut obtenir la structure suivante:
ti ® { , (dj, aij), }
Chaque terme réfère à l'ensemble de documents qui le contient et les pondérations associées. C'est cette structure qu'on appelle un fichier inversé.
Évaluation dans le modèle booléen
L'évaluation d'une requête booléenne se fera comme suit:
Si deux termes sont reliés par Ú , on utilise l'union (È ) (et le calcul de nouvelle pondération).
Évaluation dans le modèle vectoriel
Ici, on décrit seulement l'évaluation de Sim0.
additionner le produit (bi * poids du document dans cet ensemble) à la similarité du document
Dans ces deux procédures, on n'examine pas les documents l'un après l'autre. L'évaluation est faite globalement pour tous les documents concernés de la base. L'évaluation peut donc se faire très rapidement.
Réferences
Kraft, D. H. and Buell, D. A. (1983). Fuzzy sets and generalized Boolean retrieval systems. International Journal on Man-Machine Studies, 19: 49-56.
Radecki, T. (1979). Fuzzy set theoretical approach to document retrieval. Information Processing & Management, 15: 247-259.
Salton, G., Fox, E. A. and Wu, H. (1983). Extended Boolean information retrieval. Communications of the ACM, 26(12): 1022-1036.
Waller, W. G. and Kraft, D. H. (1979). A mathematical model for a weighted Boolean retrieval system. Information Processing & Management, 15: 235-245.
Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8: 338-353.