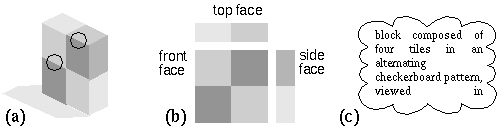
Single unit recordings from the visual cortex have been interpreted as evidence for a hierarchical model of representation in vision. According to this hypothesis, simple features are detected by low-level filters that feed into progressively more complex detectors encoding higher order features. Recognition is posited to occur at the level where the most complex features are represented. The Gestalt principle of isomorphism suggests an alternative conceptual approach, that highlights the perceptual function of top-down feedback, by way of an architecture that is both parallel and hierarchical in nature. This principle is instantiated via a bi-directional flow of information both vertically between higher and lower levels, as well as laterally between modules at the same level. A modern reformulation of isomorphism is proposed in the form of perceptual modeling, that is modeling the dynamics of perception as observed subjectively rather than the neurophysiological mechanisms by which it is subserved. This idea is illustrated with a specific model of the perception of lightness, brightness and illuminance that demonstrates how the general principles of the gestalt movement can be encoded in a computational model of perception.
Neurophysiological data from the visual cortex have been interpreted as evidence for a hierarchical organization, with lower level simple cells feeding to progressively higher level complex and hypercomplex cells. The higher level cells are often found in higher cortical areas that are specialized for processing individual perceptual modalities such as color, motion, binocular disparity, etc. This modular hierarchical organization is characteristic of algorithms proposed for computer vision (Marr 1982) in which the visual input is passed through a sequence of stages that extract progressively higher order features from the input using specialized processing modules.
There are several problems with this concept of visual processing. In the first place it does not account for feedback pathways from higher to lower level cortical areas. Furthermore, psychophysical evidence suggests integration rather than segregation between different perceptual modalities (Nakayama et al. 1990), i.e. a low level feature or structure presented in one perceptual modality has a profound effect on other perceptual modalities at that location. Finally, the feed-forward sequential processing paradigm is inconsistent with the central observation of Gestalt theory, that local features are often insufficient for identifying a global form, which is often apparent only from the global configuration rather than by the presence of local features. In fact, local features are often identifiable only by the global configuration.
The Gestalt principles of perceptual organization therefore suggest an alternative, more parallel processing architecture, with a bi-directional flow of information both bottom-up from local to global, and top-down, from global to local. This explains how a "high level" entity such as the percept of global spatial structure can influence such apparently low level entities such as the perception of surface brightness or perceived surface reflectance (lightness). The block shown in figure 1 a (from Adelson 1993) illustrates the interaction between brightness and form perception. The two circled edges separate regions of exactly the same shades of darker and lighter gray, but because of the global gestalt, one edge is perceived as a reflectance edge on a plane surface, while the other is perceived as an illuminance edge due to a corner, with no change in surface reflectance. This appears to be a low level percept since the two edges appear phenomenally quite different, especially in a more realistic photographic rendition of this phenomenon, even when one is cognitively aware of the fact that they are locally identical. An algorithm which makes decisions based only on local information would categorize these two edges as identical. The Gestalt principles suggest that perceptual processing does not proceed in a sequential feed-forward manner through successive processing stages, nor do the individual computational modules operate independently. Instead, Gestalt theory suggests that all perceptual modules operate in parallel, both at the local and the global level, and that the final percept is the result of a relaxation which emerges in a manner that is most consistent with all of the multiple interconnected modules. (The word relaxation is used to describe the changes in a dynamic system as it progresses towards its attractor, or stable state) This idea is not inconsistent with the modular architecture revealed by neurophysiology as long as the individual modules are presumed to be tightly coupled with one another in such a way that a perceptual constraint detected in any one module is simultaneously communicated to every other module. For example the pre-attentive perception of three-dimensional structure in figure 1 a constrains the circled edges to appear as a plane and a corner in depth respectively, and this in turn influences the low level perception of lightness and at those points. A close coupling across widely separated brain areas has been identified neurophysiologically in the form of synchronous oscillations (Eckhorn et al. 1988). The challenge for modeling of the perceptual process is that the individual modules must be designed so as to receive information both bottom-up from sensory input, top-down from global processing modules, as well as laterally from parallel parts of the data stream. This type of parallel accumulation of evidence from multiple sources appears to run counter to the scientific tendency to divide the problem into separate independent components, and requires novel concepts and computational principles. In particular it requires the perceptual mechanism to be defined as a multi-stable dynamic system (Attneave 1971) whose stable states are sculpted by the configuration of the input, and whose individual modules are coupled so as to produce a single globally coherent perceptual state. Central to Gestalt theory is the concept of emergence, whereby complex global scale phenomena arise spontaneously from the collective action of a multitude of simpler local forces. This concept is exemplified by a soap bubble, whose global spherical form emerges from the simultaneous action of a multitude of tiny local forces of surface tension. A model with the required properties will be of necessity rather complex, with dynamic properties that will be difficult to characterize with precision. The purpose of this paper therefore is not to present an exact computational algorithm, but rather to suggest a general computational strategy based on the Gestalt principles, for designing models of perception. A key concept of this alternative approach is the use of perceptual modeling as opposed to neural modeling, i.e. to model the dynamics of the percept as observed subjectively or as measured psychophysically. This approach must eventually converge with known neurocomputational principles. The general principles of low-level spatial computation, emergence, multistability, and perceptual modeling will be demonstrated with specific models for computing lightness, brightness, perceived illumination, and three dimensional form.
Central to this discussion is the distinction between high and low level processing. Adelson (1993) suggests that the influence of perceived spatial structure on the perception of surface brightness shown in figure 1 a reflects a high level influence on a low level percept. This idea is consistent with the conventional view of visual processing embodied in models such as Marr's Vision (1982) and Biederman's Geon theory (1987). In these models the lower levels extract simple local features such as edges, higher levels extract spatial combinations of edges, detecting such features as long continuous edges, or corners and vertices, and still higher levels extract two-dimensional enclosed surfaces defined by bounding edges and vertices. The highest levels combine information from configurations of such surfaces in order to infer the three-dimensional structure of the scene. Characteristic of this kind of processing progression are the principles of abstraction, compression, and invariance.
Abstraction represents a many-to-one combination of alternative sensory features. For example a visual edge may be defined as a dark/light or a light/dark edge in a contrast sensitive representation. A contrast-insensitive representation makes no distinction based on contrast polarity, and thus represents a more abstract, or higher level representation in the sense that it is farther from the representation seen in the visual input. Indeed lower level simple cells are contrast sensitive, while the relatively higher level complex cells are not (Hubel 1988).
Information compression is also a many-to-one relationship between a more expanded low level representation and a more compressed high level one. Attneave (1954) proposes that information compression is an essential property of visual processing in order to reduce to manageable proportions the overwhelming complexity of the visual input. Indeed the transformation from a contrast-sensitive to a contrast-insensitive representation also performs compression since every contrast-insensitive edge corresponds to two contrast-sensitive edges of opposite contrast polarity. The retinal transformation from a surface brightness image detected by retinal cones to an edge based image of the retinal ganglion cells can also be seen as information compression, since the edge image encodes only the changes at the boundaries of the luminance image.
Invariance is the property of a high level representation with respect to transformations of the low level input. For example a "node" in the brain representing a square would be invariant to perspective transformation if it were active whenever a square was present in the input, independent of its rotation, translation, or scale. This again represents a many-to-one relationship between the invariant concept and its various possible manifestations, and thus represents also both abstraction and compression.
The three principles of abstraction, compression, and invariance are generally discussed in different contexts. Abstraction is discussed in the context of symbolic representations of concrete objects. Compression is discussed in the context of information theory and computer data compression. Invariance is discussed in the context of a recognition system being tolerant to certain transformations. We propose that these concepts are intimately connected in biological vision, and that they characterize the nature of a high level representation with respect to its lower level counterpart. There are two other characteristics that are associated with a low level percept. Since the primary visual cortex has a higher resolution (in millimeters of cortex per degree of visual angle) than higher cortical areas, any percept that appears at a high spatial resolution is most likely represented at the primary visual cortex, and therefore a high spatial resolution also suggests a low level percept. A second characteristic of a low level percept is pre-attentiveness. A higher level percept is by its nature closer to cognition, and therefore is more readily influenced by cognitive factors. For example the perception of beauty or ugliness is, by this measure, a high level phenomenon. The perceived color or shape of a surface, on the other hand, is a relatively low level phenomenon, since it is less influenced by cognitive factors, which suggests processing of a lower, more automatic level.
Based on these characteristics of high versus low level representations We would argue that the perception of three-dimensional structure as seen in figure 1 a is a low level percept rather than a high level cognitive inference. This is evidenced by the fact that the spatial aspect of this percept is pre-attentive, is seen at the highest spatial resolution, and exhibits properties that are the inverse of abstraction, compression, and invariance, i.e. the percept is reified, uncompressed, and variant. Figure 1 b illustrates a three-view schematic representation of that same block depicted in figure 1 a. In this case the third dimension is not perceived directly, but is indeed inferred cognitively from the two-dimensional surfaces in the image, as suggested by Marr and Biederman. The nature of this percept however is qualitatively different from that due to figure 1 a, although the spatial information encoded in the figure is virtually identical. The information about the reflectance of the component tiles of the block and direction of the illumination source, which "pop out" pre-attentively from figure 1 a must be cognitively calculated in figure 1 b. Furthermore, the spatial information evident in figure 1 a is so complete, it is easy to hold the flat of your palm parallel to any of the three depicted surfaces, as if viewing an actual block in three-dimensions, without any conscious awareness of how this task is performed. This is in contrast to the verbal or symbolic description of the block depicted in figure 1 c which is abstracted, compressed, and invariant to perspective transformation; i.e. there are many different possible depictions such as figure 1 a all of which correspond to the single invariant description shown in figure 1 c. The influence of the spatial percept on the perception of brightness and lightness of surfaces in the figure is therefore not in the nature of a higher level inference as suggested by Adelson (1993) but rather of a lateral influence from one low level module to another.
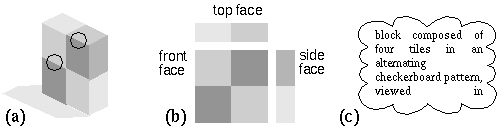
(a) Illustration (from Adelson 1993) showing how the perceived three-dimensional structure influences the local brightness percept in an image. (b) The same spatial information as in a, but requiring cognitive inference for its spatial integration. (c) A high level cognitive description of the block in a. block composed of four tiles in an alternating checkerboard pattern, viewed in perspective.
The above observations about the characteristics of higher v.s. lower level representations lead to some significant conclusions about the nature of visual processing which are contrary to the feed-forward hierarchical processing concept. Consider the Kanizsa figure, depicted in figure 2 a. It has been argued (Kennedy 1987) that the illusory contour observed in this figure represents a higher level representation or quasi-cognitive inference based on the lower level visual edges which induce it. This argument is based presumably on the fact that the illusory contour is calculated on the basis of the visible stimulus, and thus must be represented "downstream" in the processing hierarchy, in other words at a higher representational level. The inducers directly responsible for this figure however consist of local contrast-sensitive edges at the straight segments of the pac-man figures. There are two components to the percept induced by this figure; there is a higher level abstract recognition of a triangular relationship, as is seen also in figure 2 b, where the perceived triangular grouping is seen without any brightness percept. However in figure 2 a there is in addition an accompanying low level percept that consists of a visible contrast sensitive edge that is virtually indistinguishable from an actual luminance edge, as well as a percept of surface brightness which fills in the entire triangular figure with a white that is apparently whiter than the white background of the figure. In other words in this illusion, visual edges in the stimulus are seen to produce a surface brightness percept, which suggests a high level representation generating a lower level one. Furthermore, the pac-man features are not perceived as segmented circles, but are seen as complete circles which are completed amodally behind an occluding triangle. The information represented in this illusory percept therefore is something like that depicted in figure 2 c, i.e. a three-dimensional percept of a foreground bright triangle occluding three black circles on a slightly darker background. This percept has the characteristics of a low level representation because it is seen pre-attentively, at high spatial resolution, and with a specific contrast polarity. What is interesting about this and similar illusory figures is that they reveal the fact that the visual system performs the inverse of abstraction, or reification, i.e. a filling-in of a more complete and concrete representation from a less complete, more abstracted one. This immediately raises the issue whether such reification is actually performed explicitly by the visual system, or whether reification is a subjective manifestation without neurophysiological counterpart (Dennett 1991, 1992, O'Regan 1992).
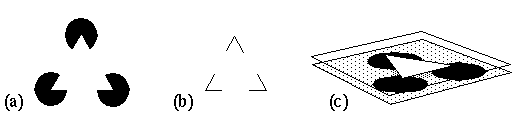
(a) The Kanizsa figure. (b) The high level triangular relationship which is a component of the percept in a. (c) The information present in the percept due to a.
The Gestalt principle of isomorphism, elaborated by Wolfgang Köhler (1938, 1947), suggests an answer to this question. Köhler argued that the nature of the internal representation can be deduced directly by inspection of the subjective percept. In a discussion of the physical mechanism of perception, a percept may refer either to a subjective experience, or to an objective state of the perceptual mechanism. The term subjective percept therefore will be used here to refer exclusively to the subjective experience of perception, independent of its physical manifestation in the system. Consider a stimulus of a white square on a black background, as shown in figure 3 a. The retinal image in response to this stimulus is a contrast-sensitive edge representation, like the one shown schematically in figure 3 b, where the light shading represents active "on" cells and the dark shading represents active "off" cells, and the neutral gray represents zero activation of either cell type. The subjective percept in response to this stimulus however is not of an edge image, but of a solid filled-in percept, as shown in figure 3 c. It has been argued (Dennett 1991, 1992) that the internal cortical representation of this stimulus need not explicitly fill-in the brightness percept because the information required for such filling-in is already implicitly present in the representation. This however would represent a violation of the principle of isomorphism, because the edge representation shown in figure 3 b is not isomorphic with the surface brightness representation shown in figure 3 c, i.e. there is no cell or variable in the representation of figure 3 b which indicates the white percept at the center of the square. Köhler argues that such a model cannot be said to model the percept at all, because there is no way to verify whether the internal representation accurately predicts the nature of the subjective percept. In an isomorphic model there must be some cell or variable or quantity at the center of the square which indicates explicitly the level of brightness perceived at that location. Note that the cell itself need not actually "turn white" to represent a perception of white, it need only be labeled "white"; i.e. the principle of isomorphism does not extend to the physical implementation of the representation, but merely to the information represented therein. In other words a mapping must be defined between the values in the internal representation and the corresponding subjective percept. In the absence of such an isomorphic relation, Köhler argues (Köhler 1971 p. 77), one would have to invoke a kind of dualism to account for the difference in informational content between the internal representation and its corresponding percept. Stated in the form of a reductio ad absurdum, if it were sufficient for the internal representation to encode perceptual information only implicitly, then there would be no need to postulate any cortical processing, because the retinal image itself already contains implicitly all the information manifest in the subjective percept.
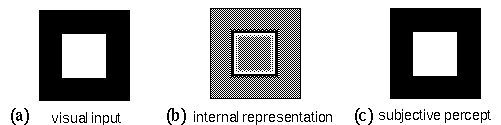
(a) An example visual input. (b) The corresponding retinal representation, where light tones represent the response of on-center cells, and dark tones represent the response of off-center cells, while the neutral gray represent no response from either cell type. (c) The subjective percept when viewing a.
The argument of isomorphism extends equally to spatial percepts such as that in figure 1 a. Whatever the actual internal representation of this three-dimensional percept, the principle of isomorphism states that the information encoded in that representation must be equivalent to the spatial information observed in the percept, i.e. with a continuous mapping in depth of every point on every visible surface. Models of spatial perception however very rarely allow for such an explicit representation of depth. Marr's 21/2-D sketch (1982) for example encodes the spatial percept as a two-dimensional map of surface orientations, like a two-dimensional array of needles pointing normal to the perceived surface. Koenderink et al. (1976, 1980, 1982) proposes a representation where each point in the two-dimensional map is labeled as either elliptic, hyperbolic, or parabolic, together with a number expressing the Gaussian curvature of the perceived surface at that point. Todd et al. (1989) propose an ordinal map where each point in the two-dimensional map records the order relations of depth and/or orientation among neighboring surface regions. Grossberg (1987 a, 1987 b) proposes a depth mapping based on disparity between two-dimensional left and right eye maps. Although both Marr and Biederman propose a three-dimensional representation to complement the 2- or 21/2-D map, the third dimension is represented exclusively in the abstract, each component geon or generalized cylinder being expressed not as a reified surface or volume, but as a set of abstract parametric variables, such as (x,y,z) location, (a,b,g) orientation, aspect ratio, central axis curvature, etc. None of these compressed representations are isomorphic with our subjective perception of a full volumetric depth world. In particular, all of these representations have a problem with encoding multiple surfaces at different depths, as in the perception of transparency, or encoding the volume of empty space that is perceived between the observer and a visible surface.
The idea of a full "tri-dimensional isomorphism" has been proposed to account for stereoscopic vision in the form of the projection field theory (Kaufman 1974, Boring 1933, Charnwood 1951, Julesz 1971) whereby the left and right eye images are projected at different angles through a three-dimensional volume of neural tissue, where their intersection defines the three-dimensional percept. However this is generally proposed only as a low-level pre-processing stage for calculating depth from binocular disparity, rather than as a generic representation of perceived space.
The gap between our subjective perception of space and our knowledge of the neurophysiological representation of three-dimensional space is so great that it seems impossible to bridge using currently accepted concepts of neural interaction. In the current neuroreductionist climate, the response to this dichotomy has been to ignore the conscious percept and to model only known physiology. An alternative approach is suggested by the Gestalt view of perception, which by the principle of isomorphism considers the subjective conscious experience as a valid source of evidence for the nature of the internal representation. We propose therefore a perceptual modeling approach, to complement the neural modeling approach, i.e. to model the percept as observed, as opposed to the neurophysiological mechanism by which it is subserved. This approach must eventually either converge with known neurophysiological knowledge, or (in our view more likely), it will highlight areas where novel computational principles and mechanisms remain to be discovered neurophysiologically.
The Gestalt approach offers a tantalizing insight into the nature of visual perception. The Gestalt soap bubble analogy (Koffka 1935, Attneave 1982) expresses the principle of emergence, in that globally coherent perceptual entities can emerge dynamically by a parallel relaxation of multiple local forces. The Gestalt soap bubble also suggests a different kind of spatial representation, for unlike the spatial representations discussed above, the soap bubble is fully reified, expressing explicitly the location of every point on the spherical surface at the highest resolution, without need for any high level global template of that form. This property of the soap bubble is isomorphic with the subjective experience of spatial perception, where every point on every perceived surface is also perceived at a precise depth. Another property of perception identified by Gestalt theory is a field-like interaction between perceptual elements, which suggests field-like forces in neural computation that seem to behave like electrical or magnetic fields, which are difficult to explain with conventional neural network architectures. Despite the appeal of this analogy of perception, the Gestalt approach has never been expressed in terms that are sufficiently specific as to suggest how such a bubble-like system would actually compute a spatial percept from a given two-dimensional image. While we do not propose to present a complete and fully specified model of perception, we do propose to advance the Gestalt soap bubble analogy one step closer to a specified computational model. In particular, we propose a specific approach to computational modeling, based on the following modeling principles:
Emergent processes - or multiple simple local interactions to achieve a coherent global percept.
Isomorphism- i.e. a perceptual model whose informational content is designed to match the information observed in the subjective percept.
Perceptual modeling - to replicate the nature of the percept resulting from a visual stimulus, rather than the neurophysiological mechanism by which that percept is supposedly subserved.
Reification - a perceptual model that fills-in or interpolates more specific spatial information than is present in the two-dimensional input on which the percept is based.
Field Theory - wherever appropriate, will be employed to model observed field-like behavior of the percept.
Multi-stability - a model whose final state is achieved by an analog relaxation in a dynamic system, so as to allow different modules to mutually influence one another dynamically.
It is difficult to fully explain the meaning of these concepts without providing specific examples. These concepts will therefore be clarified by applying these design principles to a specific set of perceptual problems. This description will begin with a model of brightness constancy and brightness contrast, then the influence of the perceived illumination will be added. In a companion paper (Lehar 1998) the discussion of isomorphism will be extended to develop a low level emergent mechanism for the perception of three-dimensional form, with mechanisms to handle the perception of brightness and illumination in a fully spatial context. The purpose of this exercise will be to clarify the meaning of these general principles by applying them to specific classical problems in perception. In so doing, we intend to identify and challenge some of the unstated assumptions underlying the more conventional approaches to visual perception. In particular, we propose to challenge the notion that perceptual processing involves principally a feed-forward progression through successive stages of feature abstraction in a modular hierarchy, whose individual modules operate either independently, or whose mutual interactions are confined to the exchange of a few high level or abstract variables.
The phenomenon of brightness contrast, illustrated in figure 4 a shows that the perceived brightness of a patch is influenced by the brightness of the surrounding region in a manner that appears to increase the contrast against the background, i.e. the gray patch on the black ground is seen as brighter than the gray patch on the white ground. This effect has been explained by lateral inhibition of the sort thought to operate in the retina, whereby cells with an on-center off-surround receptive field respond on the bright side of a contrast edge, while cells with an off-center on-surround receptive field respond on the dark side of the same edge. Figure 4 b illustrates schematically the retinal response to the stimulus in figure 4 a, with white regions representing the response of "on" cells, and dark regions representing the response of "off" cells, while the neutral gray regions represent no response from either cell type. While this kind of model has been proposed to explain the contrast effect, the responses shown in figure 4 b are not isomorphic with the percept of figure 4 a, since it is an edge representation rather than a surface brightness representation. Indeed it is hard to say from figure 4 b exactly what the corresponding brightness percept should be.
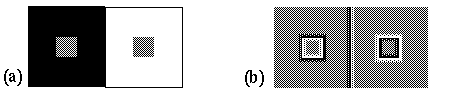
(a) The brightness contrast illusion. (b) The presumed retinal stimulus pattern while viewing a.
A number of researchers have addressed this problem by proposing models that perform a spatial derivative, as seen in retinal processing, followed by an integral to restore the surface brightness information (Land 1977, Arend 1973). The most general model of this sort is Grossberg's Boundary Contour System / Feature Contour System (BCS / FCS, Grossberg et al. 1985, 1988) because in Grossberg's model both operations are defined as local spatial operations in two dimensions rather than as analytical formulae in one dimension, and therefore this model generalizes to arbitrary two-dimensional inputs. This model also illustrates the concept of emergence, because the global perceptual state emerges from the parallel action of a multitude of tiny local forces in a dynamic feedback architecture.
Grossberg's model is summarized schematically in figure 5 using as an example an input of a white square on a black background. The first stage performs a spatial derivative, calculated by convolution with center-surround receptive fields as described above, producing a contrast-sensitive edge representation like the retinal response. The processing then splits into two parallel streams. The BCS stream produces a sharpened contrast-insensitive edge representation, i.e. cells are active along edges in the input, as indicated by the bright outline square in the figure. The FCS processing stream begins initially as a copy of the contrast-sensitive edge image of the previous stage, but a spatial diffusion operation allows the darkness and brightness signals to spread spatially in all directions, with the constraint that the diffusion is restricted by edges in the BCS image. In this case, the darkness is free to spread outwards from the outer boundary of the square, filling in a black background percept, while the brightness spreads inwards from the inner boundary of the square, filling in a white foreground percept, but the diffusing brightness and darkness signals cannot cross the boundary of the square, as represented in the BCS image.
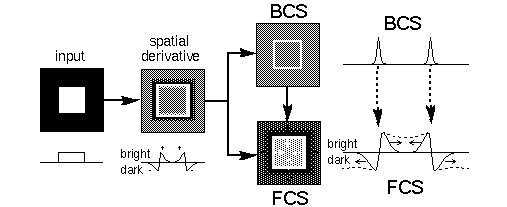
Figure 5.Schematic depiction of the processing stages of the BCS / FCS model, with intensity plots of a single scan line through the center of each image. At equilibrium the representation in the FCS becomes similar to the pattern at the input.
If the spatial derivative and spatial integration stages were mathematically exact, the integration stage would exactly invert the derivative stage, resulting in an exact copy of the input image. Due to a limited dynamic range of the representation however, (or a nonlinear saturation function applied to the spatial derivative image) large brightness steps are not registered in the same proportion as smaller brightness steps, which has the effect observed in the brightness contrast illusion, i.e. a gray patch on a dark background is restored to brighter than the original, while a gray patch on a white background is restored to darker than the original. This model therefore accounts for the brightness contrast effect in a manner that is isomorphic with the subjective percept, using mechanisms that involve local field-like interactions in a dynamic Gestalt relaxation model, to produce a globally emergent perceptual state. This model therefore serves as an example of how the Gestalt principles listed at the top of page 7 can be implemented in a computational model.
The purpose of all this processing, according to Grossberg, is to "discount the illuminant", or to implement the property of brightness constancy, whereby the intrinsic reflectance of an object is perceived despite the ambient illumination. This works because the spatial derivative image responds exclusively to local differences in illumination, and therefore any global illumination profile over large regions of the image, or broad illumination gradient with sufficiently shallow slope, will fail to register in the spatial derivative image, and will therefore not be reconstructed in the FCS image. The information represented in the model therefore can be considered a "lightness" image, or image of perceived reflectance rather than of a brightness percept.
One difference between the BCS/FCS model and the present approach is that the BCS/FCS is advanced as a neural model rather than as a perceptual model. This opens the model to criticism on the grounds of neural plausibility. For example there is a limit to the number of layers that can be included in a feedback loop that is driven by spiking neurons, due to the time required to integrate individual spikes in a postsynaptic cell. This limitation is particularly serious for the more complex model that will be presented in the companion paper (Lehar 1997) that involves even more intensive feedback than in Grossberg's model. Furthermore, considerations of neural plausibility result in unnecessary complexity in the processing algorithm, for example by the fact that a spiking neuron cannot encode negative values, and that therefore retinal on-cells and off-cells must be encoded in separate layers, rather than as positive and negative responses to a center-surround receptive field. A perceptual modeling approach on the other hand allows the model to be expressed in the simplest possible formulation required to account for the observed perceptual properties, disconfounding issues of physiology from the dynamic properties of the perceptual phenomenon being modeled.
One of the most valuable contributions of Grossberg's BCS/FCS model is the clear distinction made in this model between a modal (or "visible" in Grossberg's terminology) illusory contour and an amodal ("invisible") grouping percept. The word modal is used in the sense of brightness being a modality of perception (along with color, depth, motion, etc). An amodal grouping percept such as the one shown in figure 2 b creates a linear percept, i.e. a subject could easily trace the exact location of the perceived contour joining the vertices in this figure, and yet no brightness difference is observed along that contour. In the Kanizsa figure shown in figure 2 a on the other hand, an actual brightness difference is observed across the illusory edge, which is virtually indistinguishable from an actual luminance edge. An artist depicting the percept of the Kanizsa figure would have to use a different mix of white paint inside the triangle than outside it. The occluded segments of the three black circles in the Kanizsa figure, on the other hand, are perceived amodally, i.e. invisibly behind the occluding triangle. Since both modal and amodal contour lines are observed perceptually, and they produce distinct experiences of the illusory contour, the isomorphic model must also distinguish between modal and amodal contour percepts. In the BCS/FCS model both modal and amodal contours register in the boundary image of the BCS, but only modal contours register also on the FCS layer. The FCS representation therefore is a more low-level, direct representation of the brightness percept, whereas the BCS represents a higher level abstraction of a linear grouping percept which does not map directly to a brightness percept.
Lehar et al. (1991) proposed to rearrange the representational levels of the BCS/FCS model on the basis of the abstraction / reification distinction as depicted in figure 6. The lowest level of this model represents the surface brightness percept corresponding to the FCS image. The next level up abstracts this into a contrast sensitive edge representation corresponding to the retinal image. The next level represents another level of abstraction to a contrast insensitive edge representation, corresponding to the BCS image. Further abstraction might reduce to a representation of the corners or vertices of the image, and so on upwards through higher levels with the operations of abstraction, compression, and invariance being performed from level to level in a bottom-up manner, at the same time that the inverse operations of reification, decompression, and specification are being performed top-down from layer to layer, and further reification or figural completion is performed recurrently within each layer, completing the image in terms of the representation of the layer in question- boundary completion in edge representations and surface filling-in in surface representations.
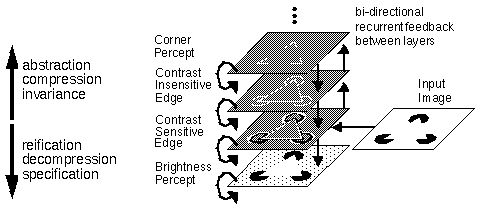
The Multi-Resonant Boundary Contour System (MRBCS) model (Lehar 1991) is similar to the BCS / FCS model except with the layers rearranged in terms of abstraction v.s. reification, i.e. lowest levels are more reified, while highest levels are more abstracted.
An interesting aspect of this model is that unlike more conventional models of vision, the retinal input is not at the lowest level of the hierarchy, but enters the hierarchy mid-stream, i.e. the actual brightness percept is a top-down reification of the retinal input, which explains how the subjective percept can encode more spatial information than the representation at the sensory surface. This makes perfect sense if the function of the visual system is to reconstruct a representation of the external world from the evidence provided by the senses, rather than to reconstruct the image on the sensory surface. Many aspects of this multi-level feedback concept were anticipated by Damasio (1989).
The operation of reification is by its nature underconstrained in that it requires information to be added to the abstracted representation. This additional information can be acquired from the local context through recurrent feedback within each layer. Consider the input of a Kanizsa figure as depicted in figure 6. Initially the contrast-sensitive edge representation (i.e. the retinal image) would register only the perimeter of each of the three pac-man features, as shown in the middle layer in figure 7 a, without any representation of the illusory contour. Abstraction upwards to the contrast-insensitive edge representation creates an image corresponding to the BCS image, again, initially representing only the outlines of the three inducing pac-man figures (figure 7 a). Recurrent feedback within this boundary layer performs collinear boundary completion as in the BCS model, generating the illusory sides of the figure by collinear completion, ( figure 7 b top layer) In a top-down reification of these contrast-insensitive edges however, the information of contrast polarity must be added to them. In the absence of any evidence of the contrast polarity of these edges, the reification must remain indeterminate, i.e. opposite contrast polarities would be given equal weight, so that no contrast boundary would appear perceptually, producing a purely amodal percept as seen in figure 2 b. In this case however the visible ends of the illusory edges do have a contrast polarity, so that contrast polarity can be filled in from the non- illusory ends to the illusory middle portions of the edge (middle layer in figure 7 c). Finally the next stage of top-down reification completes the contrast-sensitive edge representation into a full surface brightness percept by a spatial diffusion within that layer as defined in the FCS model (bottom layer figure 7 c,) producing the full Kanizsa illusion. The operations depicted sequentially in figure 7 should actually be imagined to occur in parallel, with a simultaneous emergence of mutually consistent representations at all levels of the hierarchy.
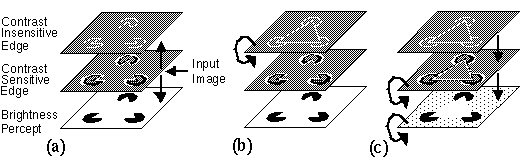
Reification in the MRBCS model: (a) the input image of three pac-man features is abstracted bottom-up to contrast-sensitive and contrast-insensitive edge representations. (b) Recurrent feedback in the edge representation completes the illusory contours. (c) The contrast-insensitive contours are reified top-down to contrast-sensitive boundaries, and finally to a surface brightness representation.
This model illustrates how the concept of a hierarchical visual representation can be resolved with the Gestalt notion of parallel relaxation in a multi-stable dynamic system to produce a final percept which is most consistent with both the bottom-up input and the top-down influence. The model also shows how top-down influence can propagate from arbitrarily high levels in the representation in such a manner as to have a direct influence on the low-level perception at the lowest levels of the hierarchy. This occurs by a progressive translation of that top-down pattern through successive intermediate representations, each of which fills-in the missing features represented at that level. This type of top-down reification is demonstrated by artists who convert an abstract invariant concept into a reified image of a particular instance of that concept viewed from a specific perspective, by carpenters and plumbers who create reified structures that begin as abstract concepts, as well as by the operation of mental imagery (Kosslyn 1994). The hierarchical models proposed by Marr (1982) and Biederman (1987) are therefore in our view not wrong, but are incomplete, representing only the bottom-up abstraction component of perception, without mention of top-down reification.
The phenomenon of brightness assimilation appears at first sight to be the exact opposite to brightness contrast. figure 8 illustrates examples of brightness assimilation. All of the gray tones in this figure are the same, but the ones which appear adjacent to black features appear blacker, whereas the ones that appear adjacent to white features appear whiter. Unlike the brightness contrast effect therefore, the gray patches assimilate the character of the adjacent color, reducing rather than increasing the contrast between them. How can a single model explain both of these apparently opposite effects?
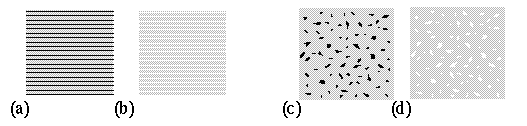
Figure 8.Brightness assimilation effect. All of the gray tones in this figure are the same shade of gray, but the gray that appears adjacent to black appears blacker, while the gray adjacent to white appears whiter. The phenomenon is influenced by spatial scale, the best assimilation being seen when viewed from greater distance.
Kanizsa (1979) reports that the necessary conditions for the occurrence of brightness assimilation, as opposed to brightness contrast involves the degree of "compactness" of the inducing surface. That is, assimilation instead of contrast takes place when the inducing surface is "dispersed" (in the form of thin lines, small disks, or fragments) into the induced surface. Taya et al. (1995) propose that the significance of this dispersion is that it changes the figure/ground relation between the fragments, making them appear as multiple components of a single larger form, rather than individual figures against a common ground. This is consistent with Helson's (1963) finding that brightness assimilation can be transformed into brightness contrast in a striped stimulus like that of figures 8 a and b by increasing the width of the stripes, because when the stripes are broad and widely separated, each stripe becomes a figure before a common ground, which promotes brightness contrast between figure and ground. When the stripes are thin and closely spaced, they are seen more like a screen, i.e. a single textured sheet, which promotes assimilation or diffusion of perceived properties in the space between the individual stripes.
The nature of the diffusion of color between the fragments is reminiscent of the diffusion mechanism of the FCS model. we propose therefore that a mechanism like the BCS/FCS model accounts for both the brightness contrast effect and the brightness assimilation effect, with the proviso that brightness contrast occurs between figure and ground, and serves to increase the contrast difference between figure and ground, whereas brightness assimilation occurs within the figure, or within the ground, serving to diminish contrast differences within the gestalt. In figure 8 a and b for example each grid of alternating colors is seen as a single gestalt, and therefore brightness assimilation occurs within that gestalt, reducing the contrast between the stripes. In figure 8 c and d the fragments appear to belong to each other, and thus they jointly define a single larger gestalt that unifies them, thereby spreading their perceptual properties by diffusion into the spaces between them. This does not of course shed any light on how the figure / ground segregation occurs, but merely suggests that the problem of contrast v.s. assimilation is related to the perception of figure v.s. ground, as suggested by Taya et al. (1995). The contribution of the Gestalt approach is that since the effects of brightness contrast and assimilation are observed to spread spatially over large regions of the image, therefore isomorphism suggests that a spatial diffusion or field-like influence is involved in generating those percepts, and Grossberg offers a dynamic computational model to account for this diffusion mechanism. The operations of brightness contrast and brightness assimilation therefore can be seen as a visual analog of the phenomenon of categorical perception in speech, where subjects are exquisitely sensitive to phonemic differences across categorical boundaries, but remarkably insensitive to phonemic differences within categorical boundaries. In vision this might be expected to "cartoonize" the image, sharpening the edges between figure and ground, while smoothing or blurring features within the figure, or within the ground, as was demonstrated by Lehar et al. (1991) with computer simulations of the MRBCS model.
The BCS / FCS model of Grossberg et al. (1985, 1988) can be described as a local ratio model, because it reconstructs the global brightness percept on the basis of locally measured contrasts across edges. A number of phenomena of brightness perception cannot be explained using local ratio models, but indicate an important contribution from the perception of the illumination pattern of the scene. One example discussed by Gilchrist et al. (1983) is the fact that a 90% reflectance square on a 30% reflectance background has the same figure/ground reflectance ratio as a 9% square on a 3% background. A ratio model such as the BCS / FCS would predict identical percepts in these cases, whereas in fact the percept is quite different, one appearing as a white square on a gray background while the other appears as a black square on a blacker background. Another condition which is problematical for the BCS / FCS model is the case where an illuminance edge is sharp, for example from a cast shadow, which would register in the spatial derivative stage, and thereby would not be discounted as an illuminant. Several researchers including Gilchrist et al. (1983) and Kanizsa (1979) have suggested that no model of brightness perception can be complete without accounting for the perception of the illuminant. Generally this is taken to mean that there must be a cognitive appreciation of the contribution of the illuminant to the low-level perception of brightness. Isomorphism suggests on the other hand that the illuminant is perceived in the same low-level pre-attentive fashion as is surface brightness, and that local low-level interactions must be invoked to factor the image into reflectance and illuminance components. This was also suggested by Gilchrist (1979).
Consider the pattern shown in figure 9 a. The nature of the intersections between the various patches of gray suggests a factorization into an illuminance percept as shown in figure 9 b, and a lightness, or reflectance percept as shown in figure 9 c. The fact that these two independent components of the image are perceived simultaneously in figure 9 a suggests by isomorphism that the perceptual representation naturally separates the percept into these perceptual components. In other words, the principle of isomorphism suggests an explicit representation of the illuminance profile, which is experienced in the same pre-attentive low-level manner as the lightness or reflectance image. This dynamic factorization could be captured in a perceptual model with an architecture as shown in figure 10. The brightness image b copies the brightness values directly from the input. This brightness information is then transferred point for point into either the illuminance image i or the lightness image l with the rule that the greater the brightness at a given point that is attributed to illuminance, the less that brightness can be attributed to surface lightness. This rule can be expressed as a dynamic interaction between nodes representing the three variables at each location as follows: activation of the brightness node bxy, representing a bright percept at a point in the image, communicates activation to both the illuminance node ixy and the lightness node lxy, for the same image location. A mutually inhibitory connection between the illuminance and the lightness nodes ensures that both cannot simultaneously be highly active, but that they must distribute the activation from the brightness node between them proportionally- the more activation taken by the one, the less activation it allows in the other. Of course the lightness and illuminance nodes are completely symmetrical, so the mutual inhibition results in a bistable system, where either node could potentially win the competition. However the percept tends to be uniform within continuous regions of the image, in other words neighboring illuminance or lightness nodes tend to be in the same state, so that when the percept flips, it does so for whole regions of the image simultaneously, rather than node by node at each point. This global bistability can be seen in the input pattern of figure 9 a, which can be seen either as a painted rectangle under a linear cast shadow, or alternatively, as a painted linear edge illuminated by a rectangular spotlight. In the latter state, the labels of figure 9 b and c would have to be reversed, to be labeled "lightness percept" and "illuminant percept" respectively. It seems more natural however to perceive the larger and simpler pattern as the illuminance percept, i.e. the two alternative states are not equally stable, but they favor the interpretation as labelled in figure 9. The figure can even be seen as simply a collection of irregular colored tiles, although this percept is the most unstable alternative. These observed properties of the percept can be expressed in the dynamic model as follows. The tendency for continuous image regions to be perceived uniformly is a field-like property, that can be modeled by a spatial coupling of adjacent nodes in the lightness and illuminance images, such that a lightness node that wins the competition with its corresponding illuminance node, would then also support adjacent lightness nodes to win their competition in the same manner, with the result that whole patches of the system would tend to flip or flop together, due to a spatial field-like interaction within each image. This coupling of adjacent nodes is however broken at visual boundaries, that are seen to separate regions of different reflectance or illuminance. This phenomenon therefore can also be modeled like the BCS/FCS system, where a spatial diffusion of reflectance or illuminance signal couples uniform regions of the image, but this diffusion is contained by visual boundaries in the image. A boundary tends to be seen either as an illuminance or a reflectance boundary, which suggests that the illuminance and the lightness images each possess their own boundary image, and a point-for-point competition between corresponding nodes in the two boundary images tend to prevent a boundary from appearing in both images simultaneously. Any particular boundary therefore would tend to settle exclusively in one or the other layer, and a boundary present in a particular layer would in turn bound the diffusion of brightness signal within that layer, thus reifying the perceived surfaces corresponding to that boundary. The system as a whole would remain bistable, i.e. the patterns in the reflectance and illuminance images depicted in figure 10 would, in the absence of a stabilizing influence, tend to spontaneously reverse, or change places. This multistability expresses the ambiguity inherent in the stimulus of figure 9 a. Although the percept is bistable, as mentioned earlier, the pattern composed of larger regions tends to be perceived as the illuminance profile. This additional soft constraint can be added to the dynamic model, for example, by providing a larger brightness diffusion constant in the illuminance image than in the lightness image. In other words, an illuminance node would have a stronger influence on neighboring illuminance nodes, so that large uniform regions would be more stable in the illuminance image than in the lightness image. While this additional influence would tend to stabilize the system in one state, the system would still remain essentially multistable, i.e. the images could potentially reverse under the influence of additional forces that support an alternative perceptual interpretation. This factorization of the brightness image into lightness and illuminance components is yet another example of reification in perception, and therefore these two extra layers would fit logically below the lowest level of the hierarchy of abstraction depicted in figure 6.
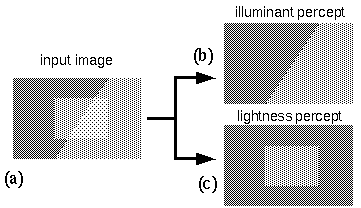
Perceptual scission of input image into two components of illumant percept and lightness percept.
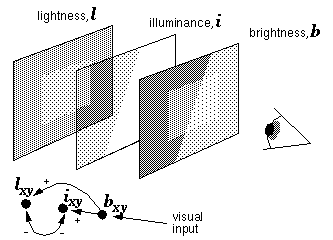
A dynamic system model of the perceptual scission of brightness into an illuminance image and a lightness image.
The details of the presented model are not important, and indeed in the companion paper (Lehar 1998) many of the details of this model will be substantially revised when considering the influence of the three-dimensional structure on the perception of brightness, lightness, and illuminance. What is important here are the general principles illustrated by this modeling approach that differ considerably from the more conventional approaches to the problem. Most significantly, the dynamic system model is presented not as a neural network architecture, or a model of neurophysiological processes, but rather as a quantified description of the dynamics of the percept as observed subjectively or as measured psychophysically. In fact, since psychophysics measures the subjective experience of perception rather than the neurophysiological state of the visual system, a perceptual model offers a more direct match to what is measured by psychophysics, as opposed to a neural network model, whose relation to subjective experience is based on as yet unproven assumptions about the mapping from neural states to subjective experience.
Many researchers have observed that the perception of lightness, brightness, illuminance, and transparency are intimately connected with the perception of depth (Bressan 1993, Coren 1972, Gilchrist 1977, 1979, Kanizsa 1979, Knill et al. 1991, Nakayama et al.1990), and indeed figure 9 a can also be perceived as a rectangle partially occluded by a dark transparent surface, or (less easily) as a straight edge seen through a dark transparent surface with a clear rectangular cut-out. These percepts involve a perceptual scission into distinct depth planes, which must also be addressed by an isomorphic model. The perception of depth however is a topic all of its own, and rather than elaborate these simple models with a few discrete depth planes, the issue of depth perception is addressed from a more general perspective in a companion paper (Lehar 1998).
The purpose of this paper was to take a new look at the old Gestalt principle of isomorphism, and to demonstrate with specific examples how certain essential Gestalt principles can be embodied in computational models of visual perception. While the resulting models remain somewhat vague, the principles are clearly expressed. Most significantly, this modeling approach suggests how global aspects of perception can be computed in an emergent manner, by a parallel relaxation of a multitude of local constraints, each of which contributes a tiny force towards the global state of the system. The separate layers or modules of this system do not operate independently, but are tightly coupled in a parallel manner to form a single multistable system whose stable states represent the final percept. Finally, the information encoded in the system is designed to replicate the information observed in the subjective percept, independent of neurophysiological considerations. This approach suggests the use of computational mechanisms, such as field-like diffusion processes, that might be considered implausible neurophysiologically, when those processes provide an accurate description of the observed dynamics of the subjective percept. We have shown that the Gestalt principles of perceptual organization can be implemented in a real physical system, that thereby offers a viable alternative, and a challenge to the often unstated and implicit assumptions underlying many of the current models of perception. In particular the assumption of a feed-forward progression of information through a hierarchical structure built of specialized and largely independent processing modules. These principles are elaborated further in a companion paper (Lehar 1998) to incorporate the perception of three-dimensional form from a monocular visual stimulus, and how that in turn influences the perception of lightness, brightness, and illuminance.
Adelson E. 1993 "Perceptual Organization and the Judgement of Brightness" Science 262 2042-2044
Arend L. 1973 "Spatial differential and integral operations in human vision: Implications of stabilized retinal image fading" Psychological Review 80 374-395.
Attneave F. 1954 "Some Informational Aspects of Visual Perception" Psychology Reviews 61 183-193
Attneave F. 1971 "Multistability in Perception" Scientific American 225 142-151
Attneave F. 1982 "Prägnanz and soap bubble systems: a theoretical exploration" in Organization and Representation in Perception, J. Beck (Ed.), Hillsdale NJ, Erlbaum.
Biederman I. 1987 "Recognition-by-Components: A Theory of Human Image Understanding". Psychological Review 94 115-147
Boring 1933 "The Physical Dimensions of Consciousness". New York: Century.
Bressan P. 1993 "Neon colour spreading with and without its figural prerequisites" Perception 22 353-361
Charnwood J. R. B. 1951 "Essay on Binocular Vision". London, Halton Press.
Coren S. 1972 "Subjective Contours and Apparent Depth" Psychological Review 79 359-367
Damasio A. R. 1989 "Time-Locked Multiregional Retroactivation: A Systems-Level Proposal in the Neural Substrates of Recall and Recognition". Cognition 33 25-62.
Dennett D. 1991 "Consciousness Explained". Boston, Little Brown & Co.
Dennett D. 1992 "`Filling In' Versus Finding Out: a ubiquitous confusion in cognitive science". In "Cognition: Conceptual and Methodological Issues, Eds. H. L. Pick, Jr., P. van den Broek, & D. C. Knill. Washington DC.: American Psychological Association.
Eckhorn R., Bauer R., Jordan W., Brosch M., Kruse W., Munk M., Reitboeck J. 1988 "Coherent Oscillations: A Mechanism of Feature Linking in the Visual Cortex?" Biol. Cybern. 60 121-130.
Gilchrist A, 1977 "Perceived lightness depends on perceived spatial arrangement" Science 195 185-187
Gilchrist A, 1979 "The Perception of Surface Blacks and Whites. Scientific American 240, 112-124.
Gilchrist A., Delman S., Jacobsen A. 1983 "The classification and integration of edges as critical to the perception of reflectance and illumination" Perception & Psychophysics 33 425-436
Grossberg S, Mingolla E, 1985 "Neural Dynamics of Form Perception: Boundary Completion, Illusory Figures, and Neon Color Spreading" Psychological Review 92 173-211
Grossberg S, (1987a) "Cortical dynamics of three-dimensional form, color and brightness perception. I. Monocular theory. Perception & Psychophysics 41 87-116
Grossberg S, (1987b) "Cortical dynamics of three-dimensional form, color and brightness perception. II. Binocular theory. Perception & Psychophysics 41 117-158
Grossberg S, Todorovic D, 1988 "Neural Dynamics of 1-D and 2-D Brightness Perception: A Unified Model of Classical and Recent Phenomena" Perception and Psychophysics 43, 241-277
Helson H. 1963 "Studies of Anomalous Contrast and Assimilation". Journal of the Optical Society of America, 53 (1), 179-184
Hubel D. 1988 "Eye, Brain, and Vision" (New York, Scientific American Library)
Julesz B. 1971 "Foundations of Cyclopean Perception". Chicago, University of Chicago Press.
Kanizsa G, 1979 "Organization in Vision" New York, Praeger.
Kaufman 1974 "Sight and Mind". New York, Oxford University Press.
Kennedy J, 1987 "Lo, Perception Abhors Not a Contradiction" In The Perception of Illusory Contours, Ed Petry S. & Meyer, G. E. (New York, Springer Verlag) 40-49.
Knill D. & Kersten D. 1991 "Apparent surface curvature affects lightness perception" Nature 351 228-230
Koenderink J. & Van Doorn A. 1976 "The singularities of the visual mapping" Biological Cybernetics 24, 51-59
Koenderink J. & Van Doorn A. 1980 "Photometric invariants related to solid shape" Optica Acta 27 981-996
Koenderink J. & Van Doorn A. 1982 "The shape of smooth objects and the way contours end" Perception 11 129-137
Koffka K, 1935 "Principles of Gestalt Psychology" New York, Harcourt Brace & Co.
Köhler W, 1938 "The Place of Value in a World of Facts". New York, Liveright.
Köhler W, 1947 "Gestalt Psychology". New York, Liveright.
Köhler W. 1971 "The Mind-Body Problem". In M. Henle (Ed.) The Selected Papers of Wolfgang Köhler. New York, Liveright, 62-82.
Kosslyn S. M. 1994 "Image and Brain: The Resolution of the Imagery Debate". Cambridge MA, MIT Press.
Land E, 1977 "Retinex theory of color vision" Scientific American 237 108-128
Lehar S. 1997 "Gestalt Isomorphism II: The Interaction Between Brightness Perception and Three-Dimensional Form". Perception (submitted).
Lehar S. & Worth A. 1991 "Multi-resonant boundary contour system" Boston University, Center for Adaptive Systems technical report CAS/CNS-TR-91-017
Marr D, 1982 "Vision". New York, W. H. Freeman.
Nakayama K, Shimojo S, Ramachandran V, 1990 "Transparency: relation to depth, subjective contours, luminance, and neon color spreading" Perception 19 497-513
O'Regan K. J., 1992 "Solving the `Real' Mysteries of Visual Perception: The World as an Outside Memory" Canadian Journal of Psychology 46 461-488.
Taya R., Ehrenstein W. H., & Cavonius C. R. 1995 "Varying the Strength of the Munker-White Effect by Stereoscopic Viewing". Perception 24 685-694.
Todd J, Reichel F, 1989 "Ordinal structure in the visual perception and cognition of smoothly curved surfaces" Psychological Review 96 643-657
Wertheimer M. 1923 "Untersuchungen zur Lehre von Gestalt. II. Psychologische Forschung 4, 301-350.