Home page: http://cns-alumni.bu.edu/pub/slehar/
email: slehar@cns.bu.edu
Submitted to Behavioral & Brain Sciences September 1999
First revision submitted April 2000
Second revision submitted September 2001
Abstract: 97, 226
Main text: 20096
References: 1884
Entire text:
24459
The subjective experience of visual perception is of a world composed of solid volumes, bounded by colored surfaces, embedded in a spatial void. These properties are difficult to relate to our neurophysiological understanding of the visual cortex. I propose therefore a perceptual modeling approach, to model the information manifest in the subjective experience of perception, as opposed to the neurophysiological mechanism by which that experience is supposedly subserved. A Gestalt Bubble model is presented to demonstrate how the dimensions of conscious experience can be expressed in a quantitative model of the perceptual experience that exhibits Gestalt properties.
A serious crisis is identified in theories of neurocomputation marked by a persistent disparity between the phenomenological or experiential account of visual perception and the neurophysiological level of description of the visual system. In particular conventional concepts of neural processing offer no explanation for the holistic global aspects of perception identified by Gestalt theory. The problem is paradigmatic, and can be traced to contemporary concepts of the functional role of the neural cell, known as the Neuron Doctrine. In the absence of an alternative neurophysiologically plausible model, I propose a perceptual modeling approach, i.e. to model the percept as experienced subjectively, rather than the objective neurophysiological state of the visual system that supposedly subserves that experience. A Gestalt Bubble model is presented to demonstrate how the elusive Gestalt principles of emergence, reification, and invariance, can be expressed in a quantitative model of the subjective experience of visual consciousness. That model in turn reveals a unique computational strategy underlying visual processing, which is unlike any algorithm devised by man, and certainly unlike the atomistic feed-forward model of neurocomputation offered by the Neuron Doctrine paradigm. The perceptual modeling approach reveals the primary function of perception as that of generating a fully spatial virtual-reality replica of the external world in an internal representation. The common objections to this "picture-in-the-head" concept of perceptual representation are shown to be ill founded.
Contemporary neuropscience finds itself in a state of serious crisis. For the deeper we probe into the workings of the brain, the farther we seem to get from the ultimate goal of providing a neurophysiological account of the mechanism of conscious experience. Nowhere is this impasse more evident than in the study of visual perception, where the apparently clear and promising trail discovered by Hubel and Wiesel leading up the hierarchy of feature detection from primary to secondary and to higher cortical areas, seems to have reached a theoretical dead-end. Besides the troublesome issues of the noisy stochastic nature of the neural signal, and the very broad tuning of the single cell as a feature detector, the notion of visual processing as a hierarchy of feature detectors seems to suggest some kind of "grandmother cell" model in which the activation of a single cell or a group of cells represents the presence of a particular type of object in the visual field. However it is not at all clear how such a featural description of the visual scene could even be usefully employed in practical interaction with the world. Alternative paradigms of neural representation have been proposed, including the suggestion that synchronous oscillations play a role in perceptual representation, although these theories are not yet specified sufficiently to know exactly how they address the issue of perceptual representation. But the most serious indictment of contemporary neurophysiological theories is that they offer no hint of an explanation for the subjective experience of visual consciousness. For visual experience is more than just an abstract recognition of the features present in the visual field, but those features are vividly experienced as solid three-dimensional objects, bounded by colored surfaces, embedded in a spatial void. There are a number of enigmatic properties of this world of experience identified decades ago by Gestalt theory, suggestive of a holistic emergent computational strategy whose operational principles remain a mystery.
The problem in modern neuroscience is a paradigmatic one, that can be traced to its central concept of neural processing. According to the Neuron Doctrine, neurons behave as quasi-independent processors separated by relatively slow chemical synapses, with strictly segregated input and output functions through the dendrites and axon respectively. It is hard to imagine how such an assembly of independent processors could account for the holistic emergent properties of perception identified by Gestalt theory. In fact the reason why these Gestalt aspects of perception have been largely ignored in recent decades is exactly because they are so difficult to express in terms of the Neuron Doctrine paradigm. More recent proposals that implicate synchronous oscillations as the neurophysiological basis of conscious experience (Crick & Koch 1990, Crick 1994, Eckhorn et al. 1988, Llinas et al. 1994) seem to suggest some kind of holistic global process that appears to be more consistent with Gestalt principles, although it is hard to see how this paradigm, at least as currently conceived, can account for the solid three-dimensional nature of subjective experience. The persistent disparity between the neurophysiological and phenomenal levels of description suggests that either the subjective experience of visual consciousness is somehow illusory, or that the state of our understanding of neural representation is far more embryonic than is generally recognized.
Pessoa et al. (1998) make the case for denying the primacy of conscious experience. They argue that although the subjective experience of filling-in phenomena is sometimes accompanied by some neurophysiological correlate, that such an isomorphism between experience and neurophysiology is not logically necessary, but is merely an empirical issue, for, they claim, subjective experiences can occur in the absence of a strictly isomorphic correlate. They argue that although the subjective experience of visual consciousness appears as a "picture" or three-dimensional model of a surrounding world, this does not mean that the information manifest in that experience is necessarily explicitly encoded in the brain. That consciousness is an illusion based on a far more compressed or abbreviated representation, in which percepts such as that of a filled-in colored surface can be explained neurophysiologically by "ignoring an absence" rather than by an explicit point-for-point mapping of the perceived surface in the brain.
In fact, nothing could be farther from the truth. For to propose that the subjective experience of perception can be more enriched and explicit than the corresponding neurophysiological state flies in the face of the materialistic basis of modern neuroscience. The modern view is that mind and brain are different aspects of the same physical mechanism. In other words, every perceptual experience, whether a simple percept such as a filled-in surface, or a complex percept of a whole scene, has two essential aspects; the subjective experience of the percept, and the objective neurophysiological state of the brain that is responsible for that subjective experience. Like the two faces of a coin, these very different entities can be identified as merely different manifestations of the same underlying structure, viewed from the internal first-person, v.s. the external third-person perspectives. The dual nature of a percept is analogous to the representation of data in a digital computer, where a pattern of voltages present in a particular memory register can represent some meaningful information, either a numerical value, or a brightness value in an image, or a character of text, etc. when viewed from inside the appropriate software environment, while when viewed in external physical terms that same data takes the form of voltages or currents in particular parts of the machine. However whatever form is selected for encoding data in the computer, the information content of that data cannot possibly be of higher dimensionality than the information explicitly expressed in the physical state of the machine. The same principle must also hold in perceptual experience, as proposed by Müller (1896), in the psychophysical postulate. Müller argued that since the subjective experience of perception is encoded in some neurophysiological state, the information encoded in that conscious experience cannot possibly be any greater than the information encoded in the corresponding neurophysiological state.While we cannot observe phenomenologically the physical medium by which perceptual information is encoded in the brain, we can observe the information encoded in that medium, expressed in terms of the variables of subjective experience. It follows therefore that it should be possible by direct phenomenological observation to determine the dimensions of conscious experience, and thereby to infer the dimensions of the information encoded neurophysiologically in the brain.
The "bottom-up" approach that works upwards from the properties of the individual neuron, and the "top-down" approach that works downwards from the subjective experience of perception are equally valid and complementary approaches to the investigation of the visual mechanism. Eventually these opposite approaches to the problem must meet somewhere in the middle. However to date, the gap between them remains as large as it ever was. Both approaches are essential to the investigation of biological vision, because each approach offers a view of the problem from its own unique perspective. The disparity between these two views of the visual representation can help focus on exactly those properties which are prominently absent from the conventional neural network view of visual processing.
There is a central philosophical issue that underlies discussions of phenomenal experience as seen for example in the distinction between the Gestaltist and the Gibsonian view of perception. That is the epistemological question of whether the world we see around us is the real world itself, or merely an internal perceptual copy of that world generated by neural processes in our brain. In other words this is the question of direct realism, also known as naive realism, as opposed to indirect realism, or representationalism. To take a concrete example, consider the vivid spatial experience of this paper that you hold in your hands. The question is whether the rich spatial structure of this experience before you is the physical paper itself, or whether it is an internal data structure or pattern of activation within your physical brain. Although this issue is not much discussed in contemporary psychology, it is an old debate that has resurfaced several times in psychology, but the continued failure to reach consensus on this issue continues to bedevil the debate on the functional role of sensory processing. The reason for the continued confusion is that both direct and indirect realism are frankly incredible, although each is incredible for different reasons.
The direct realist view is incredible because it suggests that we can have experience of objects out in the orld directly, beyond the sensory surface, as if bypassing the chain of sensory processing. For example if light from this paper is transduced by your retina into a neural signal which is transmitted from your eye to your brain, then the very first aspect of the paper that you can possibly experience is the information at the retinal surface, or the perceptual representation downstream of it in your brain. The physical paper itself lies beyond the sensory surface and therefore must be beyond your direct experience. But the perceptual experience of the page stubbornly appears out in the world itself instead of in your brain, in apparent violation of everything we know about the causal chain of vision. Gibson explicitly defended the notion of direct perception, and spoke as if perceptual processing occurs somehow out in the world itself rather than as a computation in the brain based on sensory input (Gibson 1972 p. 217 & 239). Significantly, Gibson refused to discuss sensory processing at all, and even denied that the retina records anything like a visual image that is sent to the brain. This leaves the status of the sensory organs in a peculiar kind of limbo, for if the brain does not process sensory input to produce an internal image of the world, what is the purpose of all that computational wetware? Another embarrassment for direct perception is the phenomenon of visual illusions, which are observed out in the world itself, and yet they cannot possibly be in the world, for they are the result of perceptual processing that must occur within the brain. With characteristic aplomb, Gibson simply denied that illusions are illusory at all, although it is not clear exactly what he could possibly have meant by that. Modern proponents of Gibson's theories usually take care to disclaim his most radical views (Bruce & Green 1987 p. 190, 203-204, Pessoa et al. 1998, O'Regan 1992 p. 473) but they present no viable alternative explanation to account for our experience of the world beyond the sensory surface.
The difficulty with the concept of direct perception is most clearly seen when considering how an artificial vision system could be endowed with such external perception. Although a sensor may record an external quantity in an internal register or variable in a computer, from the internal perspective of the software running on that computer, only the internal value of that variable can be "seen", or can possibly influence the operation of that software. In exactly analogous manner the pattern of electrochemical activity that corresponds to our conscious experience can take a form that reflects the properties of external objects, but our consciousness is necessarily confined to the experience of those internal effigies of external objects, rather than of external objects themselves. Unless the principle of direct perception can be demonstrated in a simple artificial sensory system, this explanation remains as mysterious as the property of consciousness it is supposed to explain.
The indirect realist view is also incredible, for it suggests that the solid stable structure of the world that we perceive to surround us is merely a pattern of energy in the physical brain, i.e. that the world that appears to be external to our head is actually inside our head. This could only mean that the head we have come to know as our own is not our true physical head, but is merely a miniature perceptual copy of our head inside a perceptual copy of the world, all of which is completely contained within our true physical skull. Stated from the internal phenomenal perspective, out beyond the farthest things you can perceive in all directions, i.e. above the dome of the sky and below the earth under your feet, or beyond the walls, floor, and ceiling of the room you perceive around you, beyond those perceived surfaces is the inner surface of your true physical skull encompassing all that you perceive, and beyond that skull is an unimaginably immense external world, of which the world you see around you is merely a miniature virtual-reality replica. The external world and its phenomenal replica cannot be spatially superimposed, for one is inside your physical head, and the other is outside. Therefore the vivid spatial structure of this page that you perceive here in your hands is itself a pattern of activation within your physical brain, and the real paper of which it is a copy it out beyond your direct experience. I have found a curious dichotomy in the response of colleagues in discussions on this issue. For many people will agree with the statement that everything you perceive is in some sense inside your head, and in fact they often complain that this is so obvious it need hardly be stated. However when that statement is turned around to say that out beyond everything you perceive is your physical skull, to this they object most vehemently as being absurd. And yet the two statements are logically identical, so how can one appear trivially obvious while the other seems patently absurd? This demostrates the value of this particular mental image, for it helps to smoke out any residual naive realism that may remain hidden in our philosophy. For although this statement can only be true in a topological, rather than a strict topographical sense, this insight emphasizes the indisputable fact that no aspect of the external world can possibly appear in consciousness except by being represented explicitly in the brain. The existential vertigo occasioned by this mental image is so disorienting that only a handful of researchers have seriously entertained this notion or pursued its implications to its logical conclusion. (Kant 1781/1991, Koffka 1935, Köhler 1971 p. 125, Russell 1927 pp 137-143, Smythies 1989, 1994, Harrison 1989, Hoffman 1998)
Another reason why the indirect realist view is incredible is that the observed properties of the world of experience when viewed from the indirect realist perspective are difficult to resolve with contemporary concepts of neurocomputation. For the world we perceive around us appears as a solid spatial structure that maintains its structural integrity as we turn around and move about in the world. Perceived objects within that world maintain their structural integrity and recognized identity as they rotate, translate, and scale by perspective in their motions through the world. These properties of the conscious experience fly in the face of everything we know about neurophysiology, for they suggest some kind of three-dimensional imaging mechanism in the brain, capable of generating three-dimensional volumetric percepts of the degree of detail and complexity observed in the world around us. No plausible mechanism has ever been identified neurophysiologically that exhibits this incredible property. The properties of the phenomenal world are therefore inconsistent with contemporary concepts of neural processing, which is exactly why these properties have been so long ignored.
There is a third alternative besides the direct and indirect realist views, and that is a projection theory, whereby the brain does indeed process sensory input, but that the results of that processing get somehow projected back out of the brain to be superimposed back on the external world (Ruch 1950 quoted in Smythies 1954, O'Shaughnessy 1980 pp 168-192, Velmans 1990, Baldwin 1992). According to this view, the world around us is part real, and part perceptual construction, and the two are spatially superimposed. However no physical mechanism has ever been proposed to account for this external projection. Velmans (1990) proposes that the percept is subserved by the neurophysiological mechanism of the brain, i.e. that every component or aspect of the projected percept has a precise neurophysiological correlate in the brain, and yet the subjective experience corresponding to those percepts is somehow back out in the world. At the same time, Velmans insists that perceptual projection is a subjective psychological effect produced by unconscious cognitive processing, and that nothing physical is actually projected from the brain. This really confounds the question of whether anything is projected at all. Smythies (1954) points out the fallacy of this theory, for if by `projection' we mean that the brain `knows' that physical objects are external to the organism, this would not explain the basic fact that the end results of the physiological processes of perception are spatially outside the physical organism.
The problem with this notion becomes clear when considering how an artificial intelligence could possibly be endowed with this kind of external projection. Although a sensor may record an external quantity in an internal register or variable in a computer, there is no sense in which that internal value can be considered to be external to that register or to the physical machine itself, whether detected externally with an electrical probe, or examined internally by software data access. Unless the principle of external projection can be demonstrated in a simple artificial sensory system, this explanation too remains as mysterious as the property of consciousness it is supposed to explain.
We are left therefore with a choice between three alternatives, each of which appears to be absolutely ncredible. Contemporary neuroscience seems to take something of an equivocal position on this issue, recognizing the epistemological limitations of the direct realist view and of the projection hypothesis, while being unable to account for the incredible properties suggested by the indirect realist view. However one of these three alternatives simply must be true, to the exclusion of the other two. And the issue is by no means inconsequential, for these opposing views suggest very different ideas of the function of visual processing, or what all that neural wetware is supposed to actually do. Therefore it is of central importance for psychology to address this issue head-on, and to determine which of these competing hypotheses reflect the truth of visual processing. For until this most central issue is resolved definitively, psychology is condemned to remain in what Kuhn (1970) calls a pre-paradigmatic state, with different camps arguing at cross-purposes due to a lack of consensus on the foundational assumptions and methodoligies of the science. For psychology is, after all, the science of the psyche, i.e. subjective side of the mind / brain barrier, and neurophysiology only enters into the picture to provide a physical substrate for mind. Therefore it is of vital importance to reach a consensus on the nature of the explanandum of psychology before we can attempt an explanans. In particular, we must decide whether the vivid spatial structure of the surrounding world of visual experience is an integral part of the psyche and thus within the explanandum of psychology, or whether it is the external world itself, as it appears to be naively, and thus in the province of physics rather than of psychology.
The problem with the direct realist view is of an epistemological nature, and is therefore a more fundamental objection, for direct realism as defended by Gibson is nothing short of magical, that we can see the world out beyond the sensory surface. The projection theory has a similar epistemological problem, and is equally magical and mysterious, suggesting that neural processes in our brain are somehow also out in the world. Both of these paradigms have difficulty with phenomena of dreams and hallucinations (Revonsuo 1995), which present the same kind of phenomenal experience as spatial vision, except independently of the external world in which that perception is supposed to occur in normal vision. It is the implicit or explicit acceptance of this naive concept of perception that has led many to conclude that consciousness is deeply mysterious and forever beyond human comprehension. For example Searle (1992 p. 96) contends that consciousness is impossible to observe, for when we attempt to observe consciousness we see nothing but whatever it is that we are conscious of; that there is no distinction between the observation and the thing observed.
The problem with the indirect realist view on the other hand is more of a technological or computational limitation, for we cannot imagine how contemporary concepts of neurocomputation, or even artificial computation for that matter, can account for the properties of perception as observed in visual consciousness. It is clear however that the most fundamental principles of neural computation and representation remain to be discovered, and therefore we cannot allow our currently limited notions of neurocomputation to constrain our observations of the nature of visual consciousness. The phenomena of dreams and hallucinations clearly demonstrate that the brain is capable of generating vivid spatial percepts of a surrounding world independent of that external world, and that capacity must be a property of the physical mechanism of the brain. Normal conscious perception can therefore be characterized as a guided hallucination (Revonsuo 1995), which is as much a matter of active construction as it is of passive detection. If we accept the truth of indirect realism, this immediately disposes of at least one mysterious or miraculous component of consciousness, which is its unobservability. For in that case consciousness is indeed observable, contrary to Searle's contention, because the objects of experience are first and foremost the product or "output" of consciousness, and only in secondary fashion are they also representative of objects in the external world. Searle's difficulty in observing consciousness is analogous to saying that you cannot see the moving patterns of glowing phosphor on your television screen, all you see is the ball game that is showing on that screen. The indirect realist view of television is that what you are seeing is first and foremost glowing phosphor patterns on a glass screen, and only in secondary fashion are those moving images also representative of the remote ball game.
The choice therefore is that either we accept a magical mysterious account of perception and consciousness that seems impossible in principle to implement in any artificial vision system, or we have to face the seemingly incredible truth that the world we perceive around us is indeed an internal data structure within our physical brain. The principal focus of neurophysiology should now be to identify the operational principles behind the three-dimensional volumetric imaging mechanism in the brain, that is responsible for the generation of the solid stable world of visual experience that we observe to surround us in conscious experience.
There have been a number of attempts in recent decades to quantify the subjective experience of visual onsciousness in computational models (see Lesher 1995 for a review). For example Zucker et al. (1988) present a model of curve completion that accounts for the emergent nature of perceptual processing by incorporating a feedback loop in which local feature detectors tuned to detect oriented edges feed up to global curvature detector cells, and those cells in turn feed back down to the local edge level to fill in missing pieces of the global curve. A similar bottom-up top-down feedback is found in Grossberg & Mingolla's (1985) visual model to account for boundary completion in illusory figures like the Kanizsa square by generating an explicit line of neural activation along the illusory contour. An extension of that model (Grossberg & Todoroviçz 1988) accounts for the filling-in of the surface brightness percept in that illusory figure, with an explicit diffusion of neural activation within the region of the illusory surface. However this approach is fraught with potential problems, for these models are expressed in neural network terms, i.e. the activation of certain cells is related to certain elements of the subjective experience. But until a mapping has been established between the conscious experience and the corresponding neurophysiological state, there is no way to verify whether the model has correctly replicated the psychophysical data. Since these models straddle the mind / brain barrier, they run headlong into the issue which Chalmers has dubbed the "hard problem" of consciousness (Chalmers 1995). Simply stated, even if we were to discover the exact neurophysiological correlates of conscious experience, there will alway remain a final explanatory gap between the physiological and the phenomenal levels of description. For example if the activation of a particular cell in the brain were found to correlate with the experience of red at some point in the visual field, there remains a vivid subjective quality, or quale, to the experience of red which is not in any way identical to any externally observable physical variable such as the electrical activity of a cell. In other words there is a subjective experiential component of perception that can never be captured in a model expressed in objective neurophysiological terms.
Even more problematic for neural models of perception is the question of whether perceptual information is expressed neurophysiologically in explicit or implicit form. For example Dennett (1992) argues that the perceptual experience of a filled-in colored surface is encoded in more abstracted form in the brain, in the manner of an edge image that records only the transitions along image edges. Support for this concept is seen in the retinal ganglion cells, that respond only along spatial or temporal discontinuities in the retinal image, and produce no response within regions of uniform color or brightness. This concept also appears to make sense from an information-theoretic standpoint, for uniform regions of color represent redundant information that can be compressed to a single value, as is the practice in image compression algorithms. These kinds of theoretical difficulties have led many neuroscientists to simply ignore the conscious experience, and to focus instead on the hard evidence of the neurophysiological properties of the brain.
The quantification of conscious experience is not quite as hopeless as it might seem. Nagel (1974) uggests that we set aside temporarily the relation between mind and brain and devise a new method of objective phenomenology, i.e. to quantify the structural features of the subjective experience in objective terms, without committing to any particular neurophysiological theory of perceptual representation. For example if we quantify the experience of vision as a three-dimensional data structure, like a model of volumes and surfaces in a surrounding space to a certain perceptual resolution, this description could be meaningful even to a congenitally blind person, or an alien creature who had never personally experienced the phenomenon of human vision. While this description could never capture everything of that experience, such as the qualia of color experience, it does at least capture the structural characteristics of that subjective experience in an objective form that would be comprehensible to beings incapable of having those experiences. Chalmers (1995) extends this line of reasoning with the observation that the subjective experience and its corresponding neurophysiological state carry the same information content. Chalmers therefore proposes a principle of structural coherence between the structure of phenomenal experience and the structure of objectively reportable awareness, to reflect the central fact that consciousness and cognition do not float free of one another, but cohere in an intimate way. In essence this is a restatement of the Gestalt principle of isomorphism, of which more later. The connecting link between mind and brain therefore is information in information-theoretic terms (Shannon 1948), because the concept of information is defined at a sufficiently high level of abstraction to be independent of any particular physical realization, and yet it is sufficiently specified as to be measurable in any physical system given that the coding scheme is known. A similar argument is made by Clark (1993, p. 50). Chalmers moderates his claim of the principle of structural coherence by stating that it is a hypothesis that is "extremely speculative". However the principle is actually solidly grounded epistemologically because the alternative is untenable. If we accept the fact that the physical states of the brain correlate directly with conscious experience, then the claim that conscious experience contains more explicit information than the physiological state on which it was based, amounts to a kind of dualism that would necessarily involve some kind of non-physical "mind stuff" to encode the excess information observed in experience that is not encoded by the physical state. Some theorists have even proposed a kind of hidden dimension of physical reality to house the unaccounted information in conscious experience (Harrison 1989, Smythies 1994).
The philosophical problems inherent in neural network models of perceptual experience can be avoided by proposing a perceptual modeling approach, as opposed to neural modeling, i.e. to model the conscious experience directly, in the subjective variables of perceived color, shape, and motion, rather than in the neurophysiological variables of neural activations or spiking frequencies etc. The variables encoded in the perceptual model therefore correspond to what philosophers call the "sense-data" or primitives of raw conscious experience, except that these variables are not supposed to be the sense-data themselves, they merely represent the value or magnitude of the sense-data that they are defined to represent. In essence this amounts to modeling the information content of subjective experience, which is the quantity that is common between the mind and brain, thus allowing an objectively quantified description of a subjective experience. In fact this approach is exactly the concept behind the description of phenomenal color space in the dimensions of hue, intensity, and saturation, as seen in the CIE chromaticity space. The geometrical dimensions of that space have been tailored to match the properties of the subjective experience of color as measured psychophysically, expressed in terms that are agnostic to any particular neurophysiological theory of color representation. Clark (1993) presents a systematic description of other sensory qualities in quantitative terms, based on this same concept of `objective phenomenology'. The thorny issue of the `hard problem' of consciousness is thus neatly side-stepped, because the perceptual model remains safely on the subjective side of the mind / brain barrier, and therefore the variables expressed in the model refer explicitly to subjective qualia rather than to neurophysiological states of the brain. The problems of explicit v.s. implicit representation are also neatly circumvented, because those issues pertain to the relation between mind and brain, and therefore they do not apply to a model that does not straddle the mind / brain barrier. For example the subjective experience of a Necker cube is of a solid three-dimensional structure, and therefore the perceptual model of that experience should also be an explicit three-dimensional structure. The spontaneous reversals of the Necker cube on the other hand are experienced as a dynamic process, and therefore that should be represented in the perceptual model as a dynamic process, i.e. as a literal reversal of the solid three-dimensional structure. The issue of whether a perceived structure can be encoded neurophysiologically as a process, or whether a perceived process can be encoded as a structure, are therefore irrelevant to the perceptual model, which by definition models a perceived structure as a structure, and a perceived process as a process.
While this is of course only an interim solution, for eventually the neurophysiological basis of conscious experience must also be identified, the perceptual model does offer objective information about the informational content encoded in the physical mechanism of the brain. This is a necessary prerequisite to a search for the neurophysiological basis of conscious experience, for we must clearly circumscribe that which we are to explain, before we can attempt an explanation of it. This approach has served psychology well in the past, particularly in the field of color perception, where the quantification of the dimensions of color experience led directly to great advances in our understanding of the neurophysiology of color vision. The failure to quantify the dimensions of spatial experience has been responsible for decades of futile debate about its neurophysiological correlates. I will show that application of this perceptual modeling approach to the realm of spatial vision opens a wide chasm between phenomenology and contemporary concepts of neurocomputation, and thereby offers a valuable check on theories of perception based principally on neurophysiological concepts.
The Gestalt principle of isomorphism represents a subtle but significant extension to Müller's psychophysical postulate, and Chalmers' principle of structural coherence. For in the case of structured experience, equal dimensionality between the subjective experience and its neurophysiological correlate implies similarity of structure or form. For example the percept of a filled-in colored surface, whether real or illusory, encodes a separate and distinct experience of color at every distinct spatial location within that surface to a particular resolution. Each point of that surface is not experienced in isolation, but in its proper spatial relation to every other point in the perceived surface. In other words the experience is extended in (at least) two dimensions, and therefore the neurophysiological correlate of that experience must also encode (at least) two dimensions of perceptual information. The mapping of phenomenal color space was established by the method of multidimensional scaling (Coren et al. 1994 p. 57) in which color values are ordered in psychophysical studies based on their perceived similarity, to determine which colors are judged to be nearest to each other, or which colors are judged to be between which other colors in phenomenal color space. A similar procedure could just as well be applied to spatial perception to determine the mapping of phenomenal space. If two points in a perceived surface are judged psychophysically to be nearer to each other when they are actually nearer, and farther when they are actually farther, and if other spatial relations such as between-ness etc. are also preserved phenomenally, this provides direct evidence that phenomenal space is mapped in a spatial representation that preserves those spatial relations in the stimulus. The outcome of this proposed experiment is so obvious it need hardly be performed. And yet its implications, that our phenomenal representation of space is spatially mapped, is not often considered in contemporary theories of spatial representation.
The isomorphism required by Gestalt theory is not a strict structural isomorphism, i.e. a literal isomorphism in the physical structure of the representation, but merely a functional isomorphism, i.e. a behavior of the system as if it were physically isomorphic (Köhler 1969, p 92). For the exact geometrical configuration of perceptual storage in the brain cannot be observed phenomenologically any more than the configuration of silicon chips on a memory card can be determined by software examination of the data stored within those chips. Nevertheless the mapping between the stored perceptual image and the corresponding spatial percept must be preserved, as in the case of the digital image also, so that every stored color value is meaningfully related to its rightful place in the spatial percept.
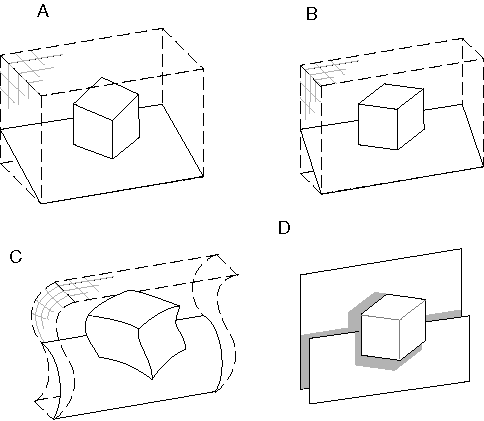
The distinction between structural and functional isomorphism can be clarified with a specific example. Consider the spatial percept of a block resting on a surface depicted schematically in figure 1 A. The information content of this perceptual experience can be captured in a painted cardboard model built explicitly like figure 1 A, i.e. with explicit volumes, bounded by colored surfaces, embedded in a spatial void. Since perceptual resolution is finite, the model should also be considered only to a finite resolution, i.e. the infinite subdivision of the continuous space of the actual model world is not considered part of the model, which can only validly represent subdivision of space to the resolution limit of perception. The same perceptual information can also be captured in quantized or digital form in a volumetric or "voxel" (volume-pixel) image in which each voxel represents a finite volume of the corresponding perceptual experience, as long as the resolution of this representation matches the spatial resolution of the percept itself, i.e. the size of the voxels should match the smallest perceivable feature in the corresponding spatial percept. Both the painted cardboard model, and its quantized voxel equivalent, are structurally or topographically isomorphic with the corresponding percept, i.e. they have the same information content as the spatial percept that they represent.

Consider now the flattened representation depicted in figure 1 B, which is identical to the model in figure 1 A except that in this case the depth dimension is compressed relative to the other two, like a bas-relief sculpture. If the defined scale of the model, i.e. the length in the representation relative to the length that it represents, is also correspondingly compressed, as suggested by the compressed grid lines in the figure, then this model is also isomorphic with the perceptual experience of figure 1 A. In other words the flattening of the depth dimension is not really registered in the model, because the perceived cube spans the same number of grid lines in figure 1 B (in all three dimensions) as it does in figure 1 A, and therefore this flattened model encodes a non-flattened perceptual experience. However this model is now no longer structurally isomorphic with the original perceptual experience, although it remains topologically isomorphic, preserving neighborhood relations, as well as between-ness etc. In a mathematical system with infinite resolution this model would encode the same information as the one in figure 1 A. However in a real physical representation there is always some limit to the resolution of the system, or how much information can be stored in each unit distance in the model itself. In a representational system with finite resolution therefore, the depth information in figure 1 B would necessarily be encoded at a lower resolution than that in the other two dimensions. If our own perceptual apparatus employed this kind of representation, this flattening would not be experienced directly; the only manifestation of the flattening of the representation would be a reduction in the resolution of perceived depth, relative to the other two dimensions, i.e. it would be more difficult to distinguish differences of perceived depth than differences of perceived height and width.
Consider now the warped model depicted in figure 1 C, which is like the flattened model of figure 1 B with a wavy distortion applied, as if warped like the gyri and sulci of the cortical surface. This warped representation is also isomorphic with the perceptual experience it represents, i.e. it encodes the same information content as the flattened space in figure 1 B, although again this is a topological rather than a topographical isomorphism. The warping of this space would not be apparent to the percipient, because the very definition of straightness is warped along with the space itself, as suggested by the warped grid lines in the figure. In contrast, consider the flattened representation depicted in figure 1 D, where the perceptual representation has been segmented into discrete depth planes, that distinguish only foreground from background objects. This model is no longer isomorphic with the perceptual experience it supposedly represents, because unlike this model, the perceptual experience manifests a specific and distinct depth value for every point in each of the surfaces of the percept. Furthermore the perceptual experience manifests an experience of empty space surrounding the perceived objects, every point of which is experienced simultaneously and in parallel as a volumetric continuum of a certain spatial resolution, whereas the model depicted in figure 1 D encodes only a small number of discrete depth planes. This kind of model therefore is inadequate as a perceptual model of the information content of conscious experience, because the dimensions of its representation are less than the dimensions of the experience it attempts to model.
Now a functional isomorphism must also preserve the functional transformations observed in perception, and the exact requirements for a functional isomorphism depend on the functionality in question. For example when a colored surface is perceived to translate coherently across perceived space, the corresponding color values in the perceptual representation of that surface must also translate coherently through the perceptual map. If that memory is discontinuous, like a digital image distributed across separate memory chips on a printed circuit board, then the perceptual representation of that moving surface must jump seamlessly across those discontinuities in order to account for the subjective experience of a continuous translation across the visual field. In other words a functional isomorphism requires a functional connectivity in the representation as if a structurally isomorphic memory were warped, distorted, or fragmented while preserving the functional connectivity between its component parts. Consider for example a representational mechanism as shown in figure 1 A, equipped with additional computational hardware capable of performing spatial transformations on the volumetric image in the representation. For example the representational mechanism might be equipped with functions which can rotate, translate, and scale the spatial pattern in the representation on demand. This representation would thereby be invariant to rotation, translation, and scale, because the spatial pattern of the block itself is encoded independent of its rotation, translation, and scale. The fact that an object in perception maintains its structural integrity and recognized identity despite rotation, translation, and scaling by perspective, is clear evidence for this kind of invariance in human perception and recognition. If the warped model shown in figure 1 C were also equipped with these same transformational functions, the warped representation would also be functionally isomorphic with the non-warped representation, as long as those transformations are performed correctly with respect to the warped geometry of that space. A functional isomorphism is even possible for a representation which is fragmented into separate pieces, so long as those pieces are wired together in such a way as to continue to perform the spatial transformations exactly the same as in the corresponding undistorted mechanism. A functional isomorphism can even survive in a volumetric representation whose individual elements or voxels are scrambled randomly across space, so long as the functional connections between those elements are preserved through the scrambling. The result is a representation which is neither topographically nor topologically isomorphic with the perceptual experience it represents. However it remains a volumetric representation, with an explicit encoding of each point in the represented space to a particular spatial resolution, and it remains functionally isomorphic with the spatial experience that it represents, capable of performing coherent rotation, translation, and scaling transformations of the perceptual structures expressed in the representation.
An explicit volumetric spatial representation capable of spatial transformation functions as described above, is more efficiently implemented in either a topographically isomorphic, or a topologically isomorphic form, which require shorter and more orderly connections between adjacent elements in the representation. However the argument for structural or topological isomorphism is an argument of representational efficiency and simplicity, rather than of logical necessity. A functional isomorphism on the other hand is strictly required in order to account for the properties of the perceptual world as observed subjectively. The volumetric structure of visual consciousness, and perceptual invariance to rotation, translation, and scale, offer direct and concrete evidence for an explicit volumetric spatial representation in the brain, which is at least functionally isomorphic with the corresponding spatial experience.
A neurophysiological model of perceptual processing and representation should concern itself with the actual mechanism in the brain. In the case of a distorted representation as suggested in figure 1 C the warping of that perceptual map would be a significant feature of the model. A perceptual model on the other hand is concerned with the structure of the percept itself, independent of any warping of the representational manifold. Even for a representation which is functionally but not structurally isomorphic, a description of the functional transformations performed in that representation are most simply expressed in their structurally isomorphic form, just as a panning or scrolling function in image data is most simply expressed as a spatial shifting of image data, even when that shifting is actually performed in hardware in a non-isomorphic memory array. Therefore the functional operation of a warped mechanism like figure 1 C is most simply described as the operation of the functionally equivalent undistorted mechanism in figure 1 A. In the present discussion therefore, our concern will be chiefly with the functional architecture of perception, i.e. a description of the spatial transformations observed in perception, whatever form those transformations might take in the physical brain, and those transformations are most simply described as if taking place in a physically isomorphic space.
The phenomenal world is composed of solid volumes, bounded by colored surfaces, embedded in a patial void. Every point on every visible surface is perceived at an explicit spatial location in three-dimensions (Clark 1993), and all of the visible points on a perceived object like a cube or a sphere, or this page, are perceived simultaneously in the form of continuous surfaces in depth. The perception of multiple transparent surfaces, as well as the experience of empty space between the observer and a visible surface, reveals that multiple depth values can be perceived at any spatial location. I propose to model the information in perception as a computational transformation from a two-dimensional colored image, (or two images in the binocular case) to a three-dimensional volumetric data structure in which every point can encode either the experience of transparency, or the experience of a perceived color at that location. The appearence of a color value at some point in this representational manifold corresponds by definition to the subjective experience of that color at the corresponding point in phenomenal space. If we can describe the generation of this volumetric data structure from the two-dimensional retinal image as a computational transformation, we will have quantified the information processing apparent in perception, as a necessary prerequisite to the search for a neurophysiological mechanism that can perform that same transformation.
This "picture-in-the-head" or "Cartesian theatre" concept of visual representation has been criticized on the grounds that there would have to be a miniature observer to view this miniature internal scene, resulting in an infinite regress of observers within observers (Dennett 1991, 1992, O'Regan 1992, Pessoa et al. 1998). In fact there is no need for an internal observer of the scene, since the internal representation is simply a data structure like any other data in a computer, except that this data is expressed in spatial form (Earle 1998, Singh & Hoffman 1998). For if a picture in the head required a homunculus to view it, then the same argument would hold for any other form of information in the brain, which would also require a homunculus to read or interpret that information. In fact any information encoded in the brain needs only to be available to other internal processes rather than to a miniature copy of the whole brain. The fact that the brain does go to the trouble of constructing a full spatial analog of the external environment merely suggests that it has ways to make use of this spatial data. For example field theories of navigation have been proposed (Koffka 1935 pp 42-46, Gibson & Crooks, 1938) in which perceived objects in the perceived environment exert spatial field-like forces of attraction and repulsion, drawing the body towards attractive percepts, and repelling it from aversive percepts, as a spatial computation taking place in a spatial medium. If the idea of an explicit spatial representation in the brain seems to "fly in the face of what we know about the neural substrates of space perception" (Pessoa et al. 1998 author's response R3.2 p. 789), it is our theories of spatial representation that are in urgent need of revision. For to deny the spatial nature of the perceptual representation in the brain is to deny the spatial nature so clearly evident in the world we perceive around us. To paraphrase Descartes, it is not only the existence of myself that is verified by the fact that I think, but when I experience the vivid spatial presence of objects in the phenomenal world, those objects are certain to exist, at least in the form of a subjective experience, with properties as I experience them to have, i.e. location, spatial extension, color, and shape. I think them, therefore they exist (Price 1932, p. 3). All that remains uncertain is whether those percepts exist also as objective external objects as well as internal perceptual ones, and whether their perceived properties correspond to objective properties. But their existence and fully spatial nature in my internal perceptual world is beyond question if I experience them so, even if only as a hallucination.
The idea of perception as a literal volumetric replica of the world inside your head immediately raises the question of boundedness, i.e. how an explicit spatial representation can encode the infinity of external space in a finite volumetric system. The solution to this problem can be found by inspection. For phenomenological examination reveals that perceived space is not infinite, but is bounded. This can be seen most clearly in the night sky, where the distant stars produce a dome-like percept that presents the stars at equal distance from the observer, and that distance is perceived to be less than infinite. The lower half of perceptual space is usually filled with a percept of the ground underfoot, but it too becomes hemispherical when viewed from far enough above the surface, for example from an airplane or a hot air balloon. The dome of the sky above, and the bowl of the earth below therefore define a finite approximately spherical space (Heelan 1983) that encodes distances out to infinity within a representational structure that is both finite and bounded. While the properties of perceived space are approximately Euclidean near the body, there are peculiar global distortions evident in perceived space that provide clear evidence of the phenomenal world being an internal rather than external entity.
Consider the phenomenon of perspective, as seen for example when standing on a long straight road that stretches to the horizon in a straight line in opposite directions. The sides of the road appear to converge to a point both up ahead and back behind, but while converging, they are also perceived to pass to either side of the percipient, and at the same time, the road is perceived to be straight and parallel throughout its entire length. This property of perceived space is so familiar in everyday experience as to seem totally unremarkable. And yet this most prominent violation of Euclidean geometry offers clear evidence for the non-Euclidean nature of perceived space. For the two sides of the road must therefore in some sense be perceived as being bowed, and yet while bowed, they are also perceived as being straight. This can only mean that the space within which we perceive the road to be embedded, must itself be curved. In fact, the observed warping of perceived space is exactly the property that allows the finite representational space to encode an infinite external space. This property is achieved by using a variable representational scale, i.e. the ratio of the physical distance in the perceptual representation relative to the distance in external space that it represents. This scale is observed to vary as a function of distance from the center of our perceived world, such that objects close to the body are encoded at a larger representational scale than objects in the distance, and beyond a certain limiting distance the representational scale, at least in the depth dimension, falls to zero, i.e. objects beyond a certain distance lose all perceptual depth. This is seen for example where the sun and moon and distant mountains appear as if cut out of paper and pasted against the dome of the sky.

The distortion of perceived space is suggested in figure 2 which depicts the perceptual representation for a man walking down a road. The phenomenon of perspective is by definition a transformation defined from a three-dimensional world through a focal point to a two-dimensional surface. The appearence of perspective on the retinal surface therefore is no mystery, and is similar in principle to the image formed by the lens in a camera. What is remarkable in perception is the perspective that is observed not on a two-dimensional surface, but somehow embedded in the three-dimensional space of our perceptual world. Nowhere in the objective world of external reality is there anything that is remotely similar to the phenomenon of perspective as we experience it phenomenologically, where a perspective foreshortening is observed not on a two-dimensional image, but in three dimensions on a solid volumetric object. The appearence of perspective in the three-dimensional world we perceive around us is perhaps the strongest evidence for the internal nature of the world of experience, for it shows that the world that appears to be the source of the light that enters our eye, must actually be downstream of the retina, for it exhibits the traces of perspective distortion imposed by the lens of the eye, although in a completely different form.
This view of perspective offers an explanation for another otherwise paradoxical but familiar property of perceived space whereby more distant objects are perceived to be both smaller, and yet at the same time to be perceived as undiminished in size. This corresponds to the difference in subject's reports depending on whether they are given objective v.s. projective instruction (Coren et al., 1994. p. 500) in how to report their observations, showing that both types of information are available perceptually. This duality in size perception is often described as a cognitive compensation for the foreshortening of perspective, as if the perceptual representation of more distant objects is indeed smaller, but is somehow labeled with the correct size as some kind of symbolic tag representing objective size attached to each object in perception. However this kind of explanation is misleading, for the objective measure of size is not a discrete quantity attached to individual objects, but is more of a continuum, or gradient of difference between objective and projective size, that varies monotonically as a function of distance from the percipient. In other words, this phenomenon is best described as a warping of the space itself within which the objects are represented, so that objects that are warped coherently along with the space in which they are embedded appear undistorted perceptually. The mathematical form of this warping will be discussed in more detail below.
This model of spatial representation emphasizes another aspect of perception that is often ignored in models of vision, that our percept of the world includes a percept of our own body within that world, and our body is located at a very special location at the center of that world, and it remains at the center of perceived space even as we move about in the external world. Perception is embodied by its very nature, for the percept of our body is the only thing that gives an objective measure of scale in the world, and a view of the world around us is useless if it is not explicitly related to our body in that world. The little man at the center of the spherical world of perception therefore is not a miniature observer of the internal scene, but is itself a spatial percept, constructed of the same perceptual material as the rest of the spatial scene, for that scene would be incomplete without a replica of the percipient's own body in his perceived world. Gibson was right therefore in his emphasis on the interaction of the active organism with its environment. Gibson's only error was the epistemological one, for Gibson failed to recognize that the organism and its environment that are active in perception are themselves internal perceptual replicas of their external counterparts. It was this epistemological confusion that led to the bizarre aspects of Gibson's otherwise valuable theoretical contributions.
One of the most formidable obstacles facing computational models of the perceptual process is that perception exhibits certain global Gestalt properties such as emergence, reification, multistability, and invariance that are difficult to account for either neurophysiologically, or even in computational terms such as computer algorithms. The ubiquity of these properties in all aspects of perception, as well as their preattentive nature suggests that Gestalt phenomena are fundamental to the nature of the perceptual mechanism. I propose that no useful progress can possibly be made in our understanding of neural processing until the computational principles behind Gestalt theory have been identified.
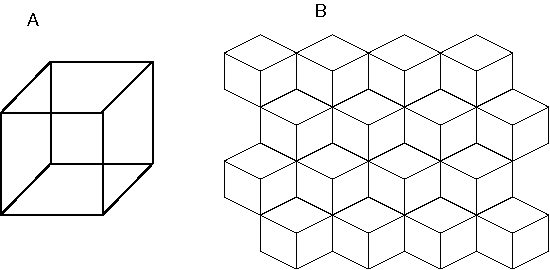
Figure 3 shows a picture that is familiar in vision circles, for it reveals the principle of emergence in a most compelling form. For those who have never seen this picture before, it appears initially as a random pattern of irregular shapes. A remarkable transformation is observed in this percept as soon as one recognizes the subject of the picture as a dalmation dog in patchy sunlight in the shade of overhanging trees. What is remarkable about this percept is that the dog is perceived so vividly despite the fact that much of its perimeter is missing. Furthermore, visual edges which form a part of the perimeter of the dog are locally indistinguishable from other less significant edges. Therefore any local portion of this image does not contain the information necessary to distinguish significant from insignificant edges.

Although Gestalt theory did not offer any specific computational mechanism to explain emergence in visual perception, Koffka (1935) suggested a physical analogy of the soap bubble to demonstrate the operational principle behind emergence. The spherical shape of a soap bubble is not encoded in the form of a spherical template or abstract mathematical code, but rather that form emerges from the parallel action of innumerable local forces of surface tension acting in unison. The characteristic feature of emergence is that the final global form is not computed in a single pass, but continuously, like a relaxation to equilibrium in a dynamic system model. In other words the forces acting on the system induce a change in the system configuration, and that change in turn modifies the forces acting on the system. The system configuration and the forces that drive it therefore are changing continuously in time until equilibrium is attained, at which point the system remains in a state of dynamic equilibrium, i.e. its static state belies a dynamic balance of forces ready to spring back into motion as soon as the balance is upset.
The Kanizsa figure (Kanzsa 1979) shown in figure 4 A, is one of the most familiar illusions introduced by Gestalt theory. In this figure the triangular configuration is not only recognized as being present in the image, but that triangle is filled-in perceptually, producing visual edges in places where no edges are present in the input, and those edges in turn are observed to bound a uniform triangular region that is brighter than the white background of the figure. Idesawa (1991) and Tse (1999a, 1999b) have extended this concept with a set of even more sophisticated illusions such as those shown in Figure 4 B through D, in which the illusory percept takes the form of a three-dimensional volume. These figures demonstrate that the visual system performs a perceptual reification, i.e. a filling-in of a more complete and explicit perceptual entity based on a less complete visual input. Reification is a general principle of perceptual processing, of which boundary completion and surface filling-in are more specific computational components. The identification of this generative aspect of perception was one of the most significant contributions of Gestalt theory.

A familiar example of multistability in perception is seen in the Necker cube, shown in Figure 5 A. Prolonged viewing of this stimulus results in spontaneous reversals, in which the entire percept is observed to invert in depth. Figure 5 B shows how large regions of the percept invert coherently in bistable fashion. Even more compelling examples of multistability are seen in surrealistic paintings by Salvator Dali, and etchings by Escher, in which large and complex regions of the image are seen to invert perceptually, losing all resemblance to their former appearence (Attneave 1971). The significance for theories of visual processing is that perception cannot be considered as simply a feed-forward processing performed on the visual input to produce a perceptual output, as it is most often characterized in computational models of vision, but rather perception must involve some kind of dynamic process whose stable states represent the final percept.
A central focus of Gestalt theory was the issue of invariance, i.e. how an object, like a square or a triangle, can be recognized regardless of its rotation, translation, or scale, or whatever its contrast polarity against the background, or whether it is depicted solid or in outline form, or whether it is defined in terms of texture, motion, or binocular disparity. This invariance is not restricted to the two-dimensional plane, but is also observed through rotation in depth, and even in invariance to perspective transformation. For example the rectangular shape of a table top is recognized even when its retinal projection is in the form of a trapezoid due to perspective, and yet when viewed from any particular perspective we can still identify the exact contours in the visual field that correspond to the boundaries of the perceived table, to the highest resolution of the visual system. The ease with which these invariances are handled in biological vision suggests that invariance is fundamental to the visual representation.
Our failure to find a neurophysiological explanation for Gestalt phenomena does not suggest that no such explanation exists, only that we must be looking for it in the wrong places. The enigmatic nature of Gestalt phenomena only highlights the importance of the search for a computational mechanism that exhibits these same properties. In the next section I present a model that demonstrates how these Gestalt principles can be expressed in a computational model that is isomorphic with the subjective experience of vision.
The basic function of visual perception can be described as the transformation from a two-dimensional retinal image, or a pair of images in the binocular case, to a solid three-dimensional percept. Figure 6 A depicts a two-dimensional stimulus that produces a three-dimensional percept of a solid cube complete in three dimensions. For simplicity, a simple line drawing is depicted in the figure, but the argument applies more appropriately to a view of a real cube observed in the world. Every point on every visible surface of the percept is experienced at a specific location in depth, and each of those surfaces is experienced as a planar continuum, with a specific three-dimensional slope in depth. The information in this perceptual experience can therefore be expressed as a three-dimensional model, as suggested in figure 6 B, constructed on the basis of the input image in figure 6 A.
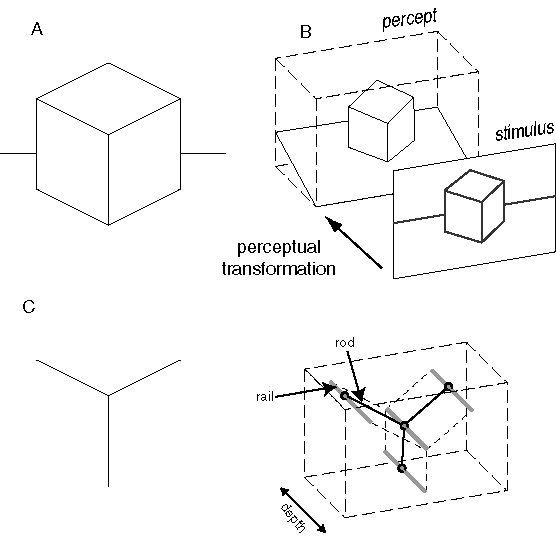
The transformation from a two-dimensional image space to a three-dimensional perceptual space is known as the inverse optics problem, since the intent is to reverse the optical projection in the eye, in which three-dimensional information from the world is collapsed into a two-dimensional image. However the inverse optics problem is underconstrained, for there are an infinite number of possible three-dimensional configurations that can give rise to the same two-dimensional projection. How does the visual system select from this infinite range of possible percepts to produce the single perceptual interpretation observed phenomenally? The answer to this question is of central significance to understanding the principles behind perception, for it reveals a computational strategy quite unlike anything devised by man, and certainly unlike the algorithmic decision sequences embodied in the paradigm of digital computation. The transformation observed in visual perception gives us the clearest insight into the nature of this unique computational strategy. I propose that the principles of emergence, reification, and multistability are intimately involved in this reconstruction, and that in fact these Gestalt properties are exactly the properties needed for the visual system to address the fundamental ambiguities inherent in reflected light imagery.
The principle behind the perceptual transformation can be expressed in general terms as follows. For any given visual input there is an infinite range of possible configurations of objects in the external world which could have given rise to that same stimulus. The configuration of the stimulus constrains the range of those possible perceptual interpretations to those that line up with the stimulus in the two dimensions of the retinal image. Now although each individual interpretation within that range is equally likely with respect to the stimulus, some of those perceptual alternatives are intrinsically more likely than others, in the sense that they are more typical of objects commonly found in the world. I propose that the perceptual representation has the property that the more likely structural configurations are also more stable in the perceptual representation, and therefore the procedure used by the visual system is to essentially construct or reify all possible interpretations of a visual stimulus in parallel, as constrained by the configuration of the input, and then to select from that range of possible percepts the most stable perceptual configuration by a process of emergence. In other words, perception can be viewed as the computation of the intersection of two sets of constraints, which might be called extrinsic v.s. intrinsic constraints. The extrinsic constraints are those determined by the visual stimulus, whereas the intrinsic constraints are determined by the structural stability of the percept.
Arnheim (1969) presents an insightful analysis of this concept, which can be reformulated as follows. Consider (for simplicity) just the central "Y" vertex of figure 6 A depicted in figure 6 C. Arnheim proposes that the extrinsic constraints of inverse optics can be expressed for this stimulus using a rod-and-rail analogy as shown in figure 6 D. The three rods, representing the three edges in the visual input, are constrained in two dimensions to the configuration seen in the input, but are free to slide in depth along four rails. The rods must be elastic between their end-points, so that they can expand and contract in length. By sliding along the rails, the rods can take on any of the infinite three-dimensional configurations corresponding to the two-dimensional input of figure 6 C. For example the final percept could theoretically range from a percept of a convex vertex protruding from the depth of the page, to a concave vertex intruding into the depth of the page, with a continuum of intermediate perceptual states between these limits. There are other possibilities beyond these, for example percepts where each of the three rods is at a different depth and therefore they do not meet in the middle of the stimulus. However these alternative perceptual states are not all equally likely to be experienced. Hochberg & Brooks (1960) showed that the final percept is the one that exhibits the greatest simplicity, or prägnanz. In the case of the vertex of figure 6 C the percept tends to appear as three rods whose ends coincide in depth at the center, and meet at a mutual right angle, defining either a concave or convex corner. This reduces the infinite range of possible configurations to two discrete perceptual states. This constraint can be expressed emergently in the rod and rail model by joining the three rods flexibly at the central vertex, and installing spring forces that tend to hold the three rods at mutual right angles at the vertex. With this mechanism in place to define the intrinsic or structural constraints, the rod-and-rail model becomes a dynamic system that slides in depth along the rails, and this system is bistable between a concave and convex right angled percept, as observed phenomenally in figure 6 C. Although this model reveals the dynamic interaction between intrinsic and extrinsic constraints, this particular analogy is hard-wired to modeling the percept of the triangular vertex of figure 6 C. I will now develop a more general model that operates on this same dynamic principle, but is designed to handle arbitrary input patterns.
For the perceptual representation I propose a volumetric block or matrix of dynamic computational elements, as suggested in figure 7 A, each of which can exist in one of two states, transparent or opaque, with opaque state units being active at all points in the volume of perceptual space where a colored surface is experienced. In other words upon viewing a stimulus like figure 6 A, the perceptual representation of this stimulus is modeled as a three-dimensional pattern of opaque state units embedded in the volume of the perceptual matrix in exactly the configuration observed in the subjective perceptual experience when viewing figure 6 A, i.e. with opaque-state elements at all points in the volumetric space that are within a perceived surface in three dimensions, as suggested in figure 6 B. All other elements in the block are in the transparent state to represent the experience of the spatial void within which perceived objects are perceived to be embedded. More generally opaque state elements should also encode the subjective dimensions of color, i.e. hue, intensity, and saturation, and intermediate states between transparent and opaque would be required to account for the perception of semi-transparent surfaces, although for now, the discussion will be limited to two states and the monochromatic case. The transformation of perception can now be defined as the turning on of the appropriate pattern of elements in this volumetric representation in response to the visual input, in order to replicate the three-dimensional configuration of surfaces experienced in the subjective percept.
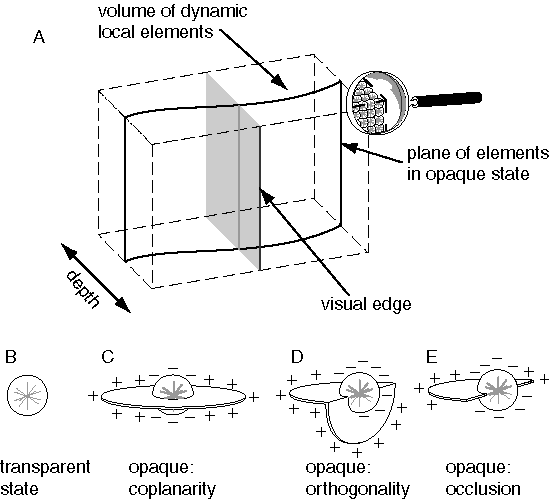
The perceived surfaces due to a stimulus like 6 A appear to span the structure of the percept defined by the edges in the stimulus, somewhat like a milky bubble surface clinging to a cubical wire frame. Although the featureless portions of the stimulus between the visual edges offer no explicit visual information, a continuous surface is perceived within those regions, as well as across the white background behind the block figure, with a specific depth and surface orientation value encoded explicitly at each point in the percept. This three-dimensional surface interpolation function can be expressed in the perceptual model by assigning every element in the opaque state a surface orientation value in three dimensions, and by defining a dynamic interaction between opaque state units to fill in the region between them with a continuous surface percept. In order to express this process as an emergent one, the dynamics of this surface interpolation function must be defined in terms of local field-like forces analogous to the local forces of surface tension active at any point in a soap bubble. Figure 7 C depicts an opaque state unit representing a local portion of a perceived surface at a specific three-dimensional location and with a specific surface orientation. The planar field of this element, depicted somewhat like a planetary ring in figure 7 C, represents both the perceived surface represented by this element, as well as a field-like influence propagated by that element to adjacent units. This planar field fades smoothly with distance from the center with a Gaussian function. The effect of this field is to recruit adjacent elements within that field of influence to take on a similar state, i.e. to induce transparent state units to switch to the opaque state, and opaque state units to rotate towards a similar surface orientation value. The final state and orientation taken on by any element is computed as a spatial average or weighted sum of the states of neighboring units as communicated through their planar fields of influence, i.e. with the greatest influence from nearby opaque elements in the matrix. The influence is reciprocal between neighboring elements, thereby defining a circular relation as suggested by the principle of emergence. In order to prevent runaway positive feedback and uncontrolled propagation of surface signal, an inhibitory dynamic is also incorporated in order to suppress surface formation out of the plane of the emergent surface, by endowing the local field of each unit with an inhibitory field in order to suppress the opaque state in neighboring elements in all directions outside of the plane of its local field. The mathematical specification of the local field of influence between opaque state units is outlined in greater detail in the appendix. However the intent of the model is expressed more naturally in the global properties as described here, so the details of the local field influences are presented as only one possible implementation of the concept, provided in order to ground this somewhat nebulous idea in more concrete terms.
The global properties of the system should be such that if the elements in the matrix were initially assigned randomly to either the transparent or opaque state, with random surface orientations for opaque-state units, the mutual field-like influences would tend to amplify any group of opaque-state elements whose planar fields happened to be aligned in an approximate plane, and as that plane of active units feeds back on its own activation, the orientations of its elements would conform ever closer to that of the plane, while elements outside of the plane would be suppressed to the transparent state. This would result in the emergence of a single plane of opaque-state units as a dynamic global pattern of activation embedded in the volume of the matrix, and that surface would be able to flex and stretch much like a bubble surface, although unlike a real bubble, this surface is defined not as a physical membrane, but as a dynamic sheet of active elements embedded in the matrix. This volumetric surface interpolation function will now serve as the backdrop for an emergent reconstruction of the spatial percept around a three-dimensional skeleton or framework constructed on the basis of the visual edges in the scene.
A visual edge can be perceived as an object in its own right, like a thin rod or wire surrounded by empty space. More often however an edge is seen as a discontinuity in a surface, either as a corner or fold, or perhaps as an occlusion edge like the outer perimeter of a flat figure viewed against a more distant background. The interaction between a visual edge and a perceived surface can therefore be modeled as follows. The two-dimensional edge from the retinal stimulus projects a different kind of field of influence into the depth dimension of the volumetric matrix, as suggested by the gray shading in figure 7 A, to represent the three-dimensional locus of all possible edges that project to the two-dimensional edge in the image. In other words, this field expresses the inverse optics probability field or extrinsic constraint due to a single visual edge. Wherever this field intersects opaque-state elements in the volume of the matrix, it changes the shape of their local fields of influence from a coplanar interaction to an orthogonal, or corner interaction as suggested by the local force field in figure 7 D. The corner of this field should align parallel to the visual edge, but otherwise remain unconstrained in orientation except by interactions with adjacent opaque units. Visual edges can also denote occlusion, and so opaque-state elements can also exist in an occlusion state, with a coplanarity interaction in one direction only, as suggested by the occlusion field in figure 7 E. Therefore, in the presence of a single visual edge, a local element in the opaque state should have an equal probability of changing into the orthogonality or occlusion state, with the orthogonal or occlusion edge aligned parallel to the inducing visual edge. Elements in the orthogonal state tend to promote orthogonality in adjacent elements along the perceived corner, while elements in the occlusion state promote occlusion along that edge. In other words, an edge will tend to be perceived as a corner or occlusion percept along its entire length, although the whole edge may change state back and forth as a unit in a multistable manner. The appendix presents a more detailed mathematical description of how these orthogonality and occlusion fields might be defined. The presence of the visual edge in figure 7 A therefore tends to crease or break the perceived surface into one of the different possible configurations shown in figure 8 A through D. The final configuration selected by the system would depend not only on the local image region depicted in figure 8, but also on forces from adjacent regions of the image, in order to fuse the orthogonal or occlusion state elements seamlessly into nearby coplanar surface percepts.
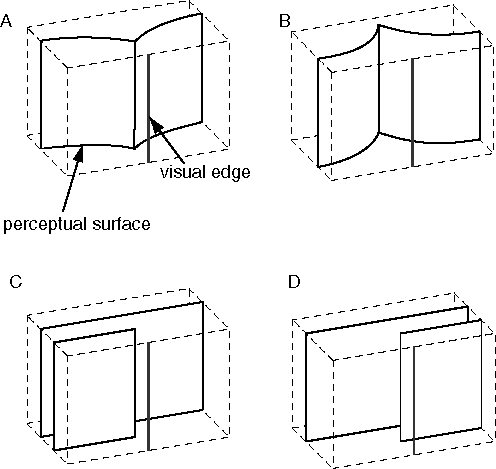
Visual illusions like the Kanizsa figure shown in figure 4 A suggest that edges in a stimulus that are in a collinear configuration tend to link up in perceptual space to define a larger global edge connecting the local edges. This kind of collinear boundary completion is expressed in this model as a physical process analogous to the propagation of a crack or fold in a physical medium. A visual edge which fades gradually produces a crease in the perceptual medium that tends to propagate outward beyond the edge as suggested in figure 9 A. If two such edges are found in a collinear configuration, the perceptual surface will tend to crease or fold between them as suggested in figure 9 B. This tendency is accentuated if additional evidence from adjacent regions support this configuration. This can be seen in figure 9 C where fading horizontal lines are seen to link up across the figure to create a percept of a folded surface in depth, which would otherwise appear as a regular hexagon, as seen in figure 9 D.
Gestalt theory emphasized the significance of closure as a prominant factor in perceptual segmentation, since an enclosed contour is seen to promote a figure / ground segregation (Koffka 1935 p. 178). For example an outline square tends to be seen as a square surface in front of a background surface that is complete and continuous behind the square, as suggested in the perceptual model depicted in figure 10 A. The problem is that closure is a "gestaltqualität", a quality defined by a global configuration that is difficult to specify in terms of any local featural requirements, especially in the case of irregular or fragmented contours as seen in figure 10 B. In this model an enclosed contour breaks away a piece of the perceptual surface, completing the background amodally behind the occluding foreground figure. In the presence of irregular or fragmented edges the influence of the individual edge fragments act collectively to break the perceptual surface along that contour as suggested in figure 10 C, like the breaking of a physical surface that is weakened along an irregular line of cracks or holes. The final scission of figure from ground is therefore driven not so much by the exact path of the individual irregular edges, as it is by the global configuration of the emergent gestalt.
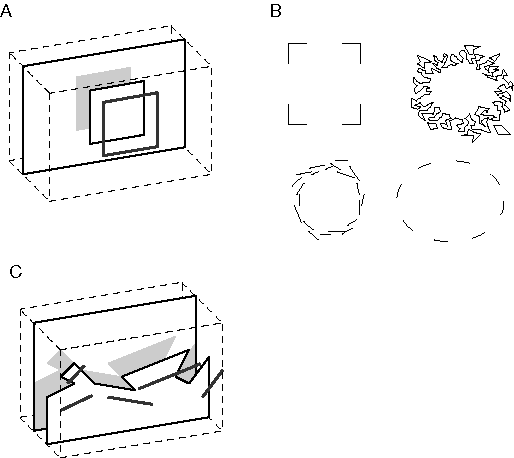
In the case of vertices or intersections between visual edges, the different edges interact with one another favoring the percept of a single vertex at that point. For example the three edges defining the three-way "Y" vertex shown in figure 6 C promote the percept of a single three-dimensional corner, whose depth profile depends on whether the corner is perceived as convex or concave. In the case of figure 6 A, the cubical percept constrains the central "Y" vertex as a convex rather than a concave trihedral percept. I propose that this dynamic behavior can be implemented using the same kinds of local field-forces described in the appendix to promote mutually orthogonal completion in three dimensions, wherever visual edges meet at an angle in two dimensions. Figure 11 A depicts the three-dimensional influence of the two-dimensional Y-vertex when projected on the front face of the volumetric matrix. Each plane of this three-planed structure promotes the emergence of a corner or occlusion percept at some depth within that plane. But the effects due to these individual edges are not independent. Consider for example, first the vertical edge projecting from the bottom of the vertex. By itself, this edge might produce a folded percept as suggested in figure 11 B, which could occur through a range of depths, and a variety of orientations in depth, and in concave or convex form. But the two angled planes of this percept each intersect the other two fields of influence due to the other two edges of the stimulus, as suggested in figure 11 B, thus favoring the emergence of those edges' perceptual folds at that same depth, resulting in a single trihedral percept at some depth in the volumetric matrix, as suggested in figure 11 C. Any dimension of this percept that is not explicitly specified or constrained by the visual input, remains unconstrained. In other words, the trihedral percept is embedded in the volumetric matrix in such a way that its three component corner percepts are free to slide inward or outward in depth, to rotate through a small range of angles, and to flip in bistable manner between a convex and concave trihedral configuration. The model now expresses the multistability of the rod-and-rail analogy shown in figure 6 D, but in a more generalized form that is no longer hard-wired to the Y-vertex input shown in figure 6 C, but can accommodate any arbitrary configuration of lines in the input image. A local visual feature like an isolated Y-vertex generally exhibits a larger number of stable states, whereas in the context of adjacent features the number of stable solutions is often diminished. This explains why the cubical percept of figure 6 A is stable, while its central Y-vertex alone as shown in figure 6 C is bistable. The fundamental multistability of figure 6 A can be revealed by the addition of a different spatial context, as depicted in figure 11 D.
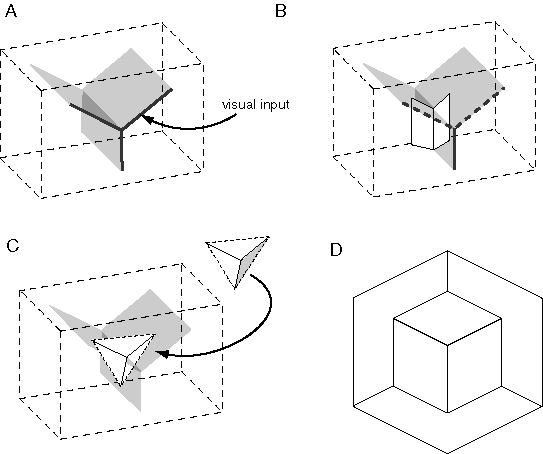
Perspective cues offer another example of a computation that is inordinately complicated in most models. However in a fully reified spatial model perspective can be computed relatively easily with only a small change in the geometry of the model. Figure 12 A shows a trapezoid stimulus, which has a tendency to be perceived in depth, i.e. the shorter top side tends to be perceived as being the same length as the longer base, but apparently diminished by perspective. Arnheim (1969) suggests a simple distortion to the volumetric model to account for this phenomenon, which can be reformulated as follows. The height and width of the volumetric matrix are diminished as a function of depth, as suggested in figure 12 B, transforming the block shape into a truncated pyramid that tapers in depth. The vertical and horizontal dimensions represented by that space however are not diminished, in other words, the larger front face and the smaller rear face of the volumetric structure represent equal areas in perceived space, by unequal areas in representational space, as suggested by the converging grid lines in the figure. All of the spatial interactions described above, for example the collinear propagation of corner and occlusion percepts, would be similarly distorted in this space. Even the angular measure of orthogonality is distorted somewhat by this transformation. For example the perceived cube depicted in the solid volume of figure 12 B is metrically shrunken in height and width as a function of depth, but since this shrinking is in the same proportion as the shrinking of the space itself, the depicted irregular cube represents a percept of a regular cube with equal sides and orthogonal faces. The propagation of the field of influence in depth due to a two-dimensional visual input on the other hand does not shrink with depth. A projection of the trapezoid of figure 12 A would occur in this model as depicted in figure 12 C, projecting the trapezoidal form backward in parallel, independent of the convergence of the space around it. The shaded surfaces in figure 12 C therefore represent the locus of all possible spatial interpretations of the two-dimensional trapezoid stimulus of figure 12 A, or the extrinsic constraints for the spatial percept due to this stimulus. For example one possible perceptual interpretation is of a trapezoid parallel to the plane of the page, which can be perceived to be either nearer or farther in depth, but since the size scale shrinks as a function of depth, the percept will be experienced as larger in absolute size (as measured against the shrunken spatial scale) when perceived as farther away, and as smaller in absolute size (as measured against the expanded scale) when perceived to be closer in depth. This corresponds to the phenomenon known as Emmert's Law (Coren et al. 1994), whereby a retinal after-image appears larger when viewed against a distant background than when viewed against a nearer background. Now there are also an infinite number of alternative perceptual interpretations of the trapezoidal stimulus, some of which are depicted by the dark shaded lines of figure 12 D. Most of these alternative percepts are geometrically irregular, representing figures with unequal sides and odd angles. But of all these possibilities, there is one special case, depicted in black lines in figure 12 D, in which the convergence of the sides of the perceived form happens to coincide exactly with the convergence of the space itself. In other words, this particular percept represents a regular rectangle viewed in perspective, with parallel sides and right angled corners, whose nearer (bottom) and farther (top) horizontal edges are the same length in the distorted perceptual space. While this rectangular percept represents the most stable interpretation, other possible interpretations might be suggested by different contexts. The most significant feature of this concept of perceptual processing is that the result of the computation is expressed not in the form of abstract variables encoding the depth and slope of the perceived rectangle, but in the form of an explicit three-dimensional replica of the surface as it is perceived to exist in the world.
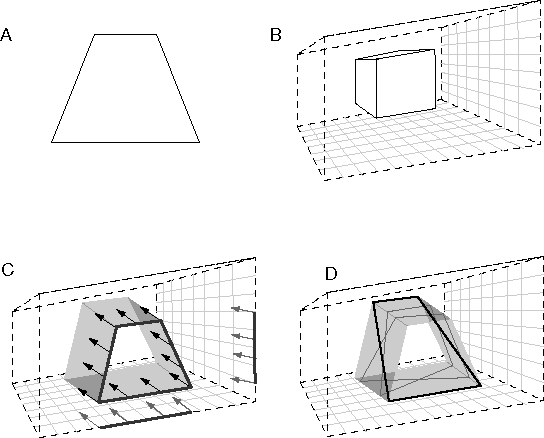
An explicit volumetric representation of perceived space as proposed here
must necessarily be bounded in some way in order to allow a finite
representational space to map to the infinity of external space, as suggested in
figure 2. The nonlinear compression of the depth dimension observed in
phenomenal space can be modeled mathematically with a vergence measure, which
maps the infinity of Euclidean distance into a finite bounded range, as
suggested in figure 13 A.This produces a representation reminiscent of museum
diaramas, like the one depicted in figure 13 B, where objects in the foreground
are represented in full depth, but the depth dimension gets increasingly
compressed with distance from the viewer, eventually collapsing into a flat
plane corresponding to the background. This vergence measure is presented here
merely as a nonlinear compression of depth in a monocular spatial
representation, as opposed to a real vergence value measured in a binocular
system, although this system could of course serve both purposes in biological
vision. Assuming unit separation between the eyes in a binocular system, this
compression is defined by the equation [ Note for HTML version: If your browser does not
load the "Symbol" font, the greek letters will not appear correctly in the text,
Pi appears as p, theta appears as q, sigma appears as s etc. If you
see proper greek letters here, this problem does not apply to you.] where n is the vergence measure of depth, and
r is the Euclidean range, or distance in depth. Actually, since vergence
is large at short range and smaller at long range, it is actually the "p-compliment" vergence measure r
that is used in the representation, where r = (p-n), and r
ranges from 0 at r = 0, to p at r =
infinity.
What does this kind of compression mean in an isomorphic representation? If
the perceptual frame of reference is compressed along with the objects in that
space, then the compression need not be perceptually apparent. Figure 13 C
depicts this kind of compressed reference grid. The unequal intervals between
adjacent grid lines in depth define intervals that are perceived to be of equal
length, so the flattened cubes defined by the distorted grid would appear
perceptually as regular cubes, of equal height, breadth, and depth. This
compression of the reference grid to match the compression of space would, in a
mathematical system with infinite resolution, completely conceal the compression
from the percipient. In a real physical implementation there are two effects of
this compression that would remain apparent perceptually, due to the fact that
the spatial matrix itself would have to have a finite perceptual resolution. The
resolution of depth within this space is reduced as a function of depth, and
beyond a certain limiting depth, all objects are perceived to be flattened into
two dimensions, with zero extent in depth. This phenomenon is observed
perceptually, where the sun, moon, and distant mountains appear as if they are
pasted against the flat dome of the sky. The other two dimensions of space can also be bounded by converting the
x and y of Euclidean space into azimuth and elevation angles,
a and b, producing an angle /
angle / vergence representation, as shown in figure 14 A. Mathematically this
transformation converts the point P(a,b,r) in polar coordinates to point Q(a,b,r) in
this bounded spherical representation. In other words, azimuth and elevation
angles are preserved by this transformation while the radial distance in depth
r is compressed to the vergence representation r
as described above. This spherical coordinate system has the ecological
advantage that the space near the body is represented at the highest spatial
resolution, whereas the less important more distant parts of space are
represented at lower resolution. All depths beyond a certain radial distance are
mapped to the surface of the representation which corresponds to perceptual
infinity.
The mathematical form of this distortion is depicted in figure 14 B, where
the distorted grid depicts the perceptual representation of an infinite
Cartesian grid with horizontal and vertical grid lines spaced at equal
intervals. This geometrical transformation from the infinite Cartesian grid
actually represents a unique kind of perspective transformation on the Cartesian
grid. In other words, the transformed space looks like a perspective view of a
Cartesian grid when viewed from inside, with all parallel lines converging to a
point in opposite directions. The significance of this observation is that by
mapping space into a perspective-distorted grid, the distortion of perspective
is removed, in the same way that plotting log data on a log plot removes the
logarithmic component of the data. Figure 14 C shows how this space would
represent the perceptual experience of a man walking down a road. If the
distorted reference grid of figure 14 B is used to measure lines and distances
in figure 14 C, the bowed line of the road on which the man is walking is
aligned with the bowed reference grid and therefore is perceived to be straight.
Therefore the distortion of straight lines into curves in the perceptual
representation is not immediately apparent to the percipient, because they are
perceived to be straight. However in a global sense there are peculiar
distortions that are apparent to the percipient caused by this deformation of
Euclidean space. For while the sides of the road are perceived to be parallel,
they are also perceived to meet at a point on the horizon. The fact that two
lines can be perceived to be both straight and parallel and yet to converge to a
point both in front and behind the percipient indicates that our internal
representation itself must be curved. The proposed representation of space has
exactly this property. Parallel lines do not extend to infinity but meet at a
point beyond which they are no longer represented. Likewise the vertical walls
of the houses in figure 14 C bow outwards away from the observer, but in doing
so they follow the curvature of the reference lines in the grid of figure 14 B,
and are therefore perceived as being both straight, and vertical. Since curved
lines in this spherical representation represent straight lines in external
space, all of the spatial interactions discussed in the previous section,
including the coplanar interactions, and collinear creasing of perceived
surfaces, must follow the grain or curvature of collinearity defined within this
distorted coordinate system. The distance scale encoded in the grid of figure 14
B replaces the regularly spaced Cartesian grid by a nonlinear collapsing grid
whose intervals are spaced ever closer as they approach perceptual infinity but
nevertheless represent equal intervals in external space. This nonlinear
collapsing scale thereby provides an objective measure of distance in the
perspective-distorted perceptual world. For example the houses in figure 14 C
would be perceived to be approximately the same size and depth, although the
farther house is experienced at a lower perceptual resolution. Figure 14 D depicts how a slice of Euclidean space of fixed height and width
would appear in the perceptual sphere, extending to perceptual infinity in one
direction, like a slice cut from the spherical representation of figure 14 C.
This slice is similar to the truncated pyramid shape shown in figure 12 B, with
the difference that the horizontal and vertical scale of representational space
diminishes in a nonlinear fashion as a function of distance in depth. In other
words, the sides of the pyramid in figure 14 B converge in curves rather than in
straight lines, and the pyramid is no longer truncated, but extends in depth all
the way to the vanishing point at representational infinity. An input image is
projected into this spherical space using the same principles as before. One of the most disturbing properties of the phenomenal world for models of
the perceptual mechanism involves the subjective impression that the phenomenal
world rotates relative to our perceived head as our head turns relative to the
world, and that objects in perception are observed to translate and rotate while
maintaining their perceived structural integrity and recognized identity. This
suggests that the internal representation of external objects and surfaces is
not anchored to the tissue of the brain, as suggested by current concepts of
neural representation, but that perceptual structures are free to rotate and
translate coherently relative to the neural substrate, as suggested in Köhler's
field theory (Köhler & Held 1947). This issue of brain anchoring is so
troublesome that it is often cited as a counter-argument for an isomorphic
representation, since it is difficult to conceive of the solid spatial percept
of the surrounding world having to be reconstructed anew in all its rich spatial
detail with every turn of the head (Gibson 1979, O'Regan 1992). However an
argument can be made for the adaptive value of a neural representation of the
external world that could break free of the tissue of the sensory or cortical
surface in order to lock on to the more meaningful coordinates of the external
world, if only a plausible mechanism could be conceived to achieve this useful
property. Even in the absence of a neural model with the required properties, the
invariance property can be encoded in a perceptual model. In the case of
rotation invariance, this property can be quantified by proposing that the
spatial structure of a perceived object and its orientation are encoded as
separable variables. This would allow the structural representation to be
updated progressively from successive views of an object that is rotating
through a range of orientations. However the rotation invariance property does
not mean that the encoded form has no defined orientation, but rather that the
perceived form is presented to consciousness at the orientation and rate of
rotation that the external object is currently perceived to possess. In other
words, when viewing a rotating object, like a person doing a cartwheel, or a
skater spinning about her vertical axis, every part of that visual stimulus is
used to update the corresponding part of the internal percept even as that
percept rotates within the perceptual manifold to remain in synchrony with the
rotation of the external object. The perceptual model need not explain how this
invariance is achieved neurophysiologically, it must merely express the
invariance property computationally, regardless of the "neural plausibility" or
computational efficiency of that calculation. For the perceptual model is more a
quantitative description of the phenomenon rather than a theory of
neurocomputation. The property of translation invariance can be similarly
quantified in the representation by proposing that the structural representation
can be calculated from a stimulus that is translating across the sensory
surface, to update a perceptual effigy that translates with respect to the
representational manifold, while maintaining its structural integrity. This
accounts for the structural constancy of the perceived world as it scrolls past
a percipient walking through a scene, with each element of that scene following
the proper curved perspective lines as depicted in figure 2, expanding outwards
from a point up ahead, and collapsing back to a point behind, as would be seen
in a cartoon movie rendition of figure 2. The fundamental invariance of such a representation offers an explanation for
another property of visual perception, i.e. the way that the individual
impressions left by each visual saccade are observed to appear phenomenally at
the appropriate location within the global framework of visual space depending
on the direction of gaze. This property can be quantified in the perceptual
model as follows. The two-dimensional image from the spherical surface of the
retina is copied onto a spherical surface in front of the eyeball of the
perceptual effigy, from whence the image is projected radially outwards in an
expanding cone into the depth dimension of the internal perceptual world as
suggested in figure 15, as an inverse analog of the cone of light received from
the world by the eye. Eye, head, and body orientation relative to the external
world are taken into account in order to direct the visual projection of the
retinal image into the appropriate sector of perceived space, as determined from
proprioceptive and kinesthetic sensations in order to update the image of the
body configuration relative to external space. The percept of the surrounding
environment therefore serves as a kind of three-dimensional frame buffer
expressed in global coordinates, that accumulates the information gathered in
successive visual saccades and maintains an image of that external environment
in the proper orientation relative to a spatial model of the body, compensating
for body rotations or translations through the world. Portions of the
environment that have not been updated recently gradually fade from perceptual
memory, which is why it is easy to bump one's head after bending for some time
under an overhanging shelf, or why it is possible to advance only a few steps
safely after closing one's eyes while walking.
The picture of visual processing revealed by the phenomenological approach is
radically different from the picture revealed by neurophysiological studies. In
fact, the computational transformations observed phenomenologically are
implausible in terms of contemporary concepts of neurocomputation and even in
terms of computer algorithms. However the history of psychology is replete with
examples of plausibility arguments based on the limited technology of the time
which were later invalidated by the emergence of new technologies. The
outstanding achievements of modern technology, especially in the field of
information processing systems, might seem to justify our confidence to judge
the plausibility of proposed processing algorithms. And yet, despite the
remarkable capabilities of modern computers, there remain certain classes of
problems that appear to be fundamentally beyond the capacity of the digital
computer. In fact the very problems that are most difficult for computers to
address, such as extraction of spatial structure from a visual scene especially
in the presence of attached shadows, cast shadows, specular reflections,
occlusions, perspective distortions, as well as the problems of navigation in a
natural environment, etc. are problems that are routinely handled by biological
vision systems, even those of simpler animals. On the other hand, the kinds of
problems that are easily solved by computers, such as perfect recall of vast
quantities of meaningless data, perfect memory over indefinite periods,
detection of the tiniest variation in otherwise identical data, exact
repeatability of even the most complex computations, are the kinds of problems
that are inordinately difficult for biological intelligence, even that of the
most complex of animals. It is therefore safe to assume that the computational
principles of biological vision are fundamentally different from those of
digital computation, and therefore plausibility arguments predicated on
contemporary concepts of what is computable are not applicable to biological
vision. If we allow that our contemporary concepts of neurocomputation are so
embryonic that they should not restrict our observations of the phenomenal
properties of perception, the evidence for a Gestalt Bubble model of perceptual
processing becomes overwhelming. The phenomena of hallucinations and dreams demonstrate that the mind is
capable of generating complete spatial percepts of the world, including a
percept of the body and the space around it (Revonsuo 1995). It is unlikely that
this remarkable capacity is used only to create such illusory percepts. More
likely, dreams and hallucinations reveal the capabilities of an imaging system
that is normally driven by the sensory input, generating perceptual constructs
that are coupled to external reality. Studies of mental imagery (Kosslyn 1980, 1994) have characterized the
properties of this imaging capacity, and confirmed the three-dimensional nature
of the encoding and processing of mental imagery. Pinker (1980) shows that the
scanning time between objects in a remembered three-dimensional scene increases
linearly with increasing distance between objects in three dimensions. Shepard
& Metzler. (1971) show that the time for rotation of mental images is
proportional to the angle through which they are rotated. Kosslyn shows that it
takes time to expand the size of mental images, and that smaller mental images
are more difficult to scrutinize (Kosslyn 1975). As unexpected as these findings
may seem for theorists of neural representation, they are perfectly consistent
with the subjective experience of mental imagery. On the basis of these
findings, Pinker (1988) derived a volumetric spatial medium to account for the
observed properties of mental image manipulation which is very similar to the
model proposed here, i.e. with a volumetric azimuth/elevation coordinate system
that is addressable both in subjective viewer-centered, and objective
viewer-independent coordinates, and with a compressive depth scale. The phenomenon of hemi-neglect (Kolb & Whishaw 1996) reveals the effects
of damage to the spatial representation, destroying the capacity to represent
spatial percepts in one half of phenomenal space. Such patients are not simply
blind to objects to one side, but are blind to the very existence of a space in
that direction as a potential holder of objects. For example, neglect patients
will typically eat food only from the right half of their plate, and express
surprise at the unexpected appearance of more food when their plate is rotated
180 degrees. This condition even persists when the patient is cognitively aware
of their deficit (Sacks 1985). Bisiach et al. (1978,1981) show how this
condition can also impair mental imaging ability. They describe a neglect
patient who, when instructed to recall a familiar scene viewed from a certain
direction, can recall only objects from the right half of his remembered space.
When instructed to mentally turn around and face in the opposite direction, the
patient now recalls only objects from the other side of the scene, that now fall
in the right half of his mental image space. The condition of hemi-neglect
therefore suggests damage to the left half of a three-dimensional imaging
mechanism that is used both for perception and for the generation of mental
imagery. Note that hemi-neglect also includes a neglect of the left side of the
body, which is consistent with the fact that the body percept is included as an
integral part of the perceptual representation. Whatever the physiological
reality behind the phenomenon of hemi-neglect, the Gestalt Bubble model offers
at least a concrete description of this otherwise paradoxical phenomenon. The idea that this spatial imaging system employs an explicit volumetric
spatial representation is suggested by the fact that disparity tuned cells have
been found in the cortex (Barlow et al. 1967), as predicted by the
Projection Field Theory of binocular vision (Kaufman 1974, Boring 1933,
Charnwood 1951, Marr & Poggio 1976, Julesz 1971), which is itself a
volumetric model. Psychophysical evidence for a volumetric representation comes
from the fact that perceived objects in depth exhibit attraction and repulsion
in depth (Westheimer & Levi 1987, Mitchison 1993) in a manner that is
suggestive of a short-range attraction and longer-range repulsion in depth,
analogous to the center-surround processing in the retina. Brookes & Stevens
(1989) discuss the analogy between brightness and depth perception, and show
that a number of brightness illusions that have been attributed to such
center-surround processing have corresponding illusions in depth. Similarly,
Anstis & Howard (1978) have demonstrated a Craik-O'Brien-Cornsweet illusion
in depth by cutting the near surface of a block of wood with a depth profile
matching the brightness cusp of the brightness illusion, resulting in an
illusory percept of a difference in depth of the surfaces on either side of the
cusp. As in the brightness illusion, therefore, the depth difference at the cusp
appears to propagate a perceptual influence out to the ends of the block,
suggesting a spatial diffusion of depth percept between depth edges. The many manifestations of constancy in perception have always posed a
serious challenge for theories of perception because they reveal that the
percept exhibits properties of the distal object rather than the proximal
stimulus, or pattern of stimulation on the sensory surface. The Gestalt Bubble
model explains this by the fact that the information encoded in the internal
perceptual representation itself reflects the properties of the distal object
rather than the proximal stimulus. Size constancy is explained by the fact that
objects perceived to be more distant are represented closer to the outer surface
of the perceptual sphere, where the collapsing reference grid corrects for the
shrinkage of the retinal image due to perspective. An object perceived to be
receding in depth therefore is expected perceptually to shrink in retinal size
along with the shrinking of the grid in depth, and conversely, shrinking objects
tend to be perceived as receding. Rock & Brosgole. (1964), show that
perceptual grouping by proximity is determined not by proximity in the
two-dimensional retinal projection of the figure, but rather by the
three-dimensional perceptual interpretation. A similar finding is shown by Green
& Odum (1986). Shape constancy is exemplified by the fact that a rectangle
seen in perspective is not perceived as a trapezoid, as its retinal image would
suggest. The Müller-Lyer and Ponzo illusions are explained in similar fashion
(Tausch 1954, Gregory 1963, Gillam 1971, 1980), the converging lines in those
figures suggesting a surface sloping in depth, so that features near the
converging ends are measured against a more compressed reference grid than the
corresponding feature near the diverging ends of those lines. Several researchers have presented psychophysical evidence for a spatial
interpolation in depth, which is difficult to account for except with a
volumetric representation in which the interpolation is computed explicitly in
depth (Attneave 1982). Kellman et al. (1996) have demonstrated a coplanar
completion of perceived surfaces in depth in a manner analogous to the collinear
completion in the Kanizsa figure. Barrow & Tenenbaum (1981, p. 94 and Figure
6.1) show how a two-dimensional wire-frame outline held in front of a dynamic
random noise pattern stimulates a three-dimensional surface percept spanning the
outline like a soap film, and that perceived surface undergoes a Necker reversal
together with the reversal of the perimeter wire. Ware & Kennedy (1978) have
shown that a three-dimensional rendition of the Ehrenstein illusion constructed
of a set of rods converging on a circular hole, creates a three-dimensional
version of the illusion that is perceived as a spatial structure in depth, even
when rotated out of the fronto-parallel plane, complete with a perception of
brightness at the center of the figure. This illusory percept appears to hang in
space like a faintly glowing disk in depth, reminiscent of the neon color
spreading phenomenon. A similar effect can be achieved with a three-dimensional
rendition of the Kanizsa figure. If the Ehrenstein and Kanizsa figures are
explained by spatial interpolation in models such as Grossberg & Mingolla
(1985), then the corresponding three-dimensional versions of these illusions
must involve a volumetric computational matrix to perform the interpolation in
depth. Collett (1985) has investigated the interaction between monocular and
binocular perception using stereoscopically presented line drawings in which
some features are presented only monocularly, i.e. their depth information is
unspecified. Collett shows that such features tend to appear perceptually at the
same depth as adjacent binocularly specified features, as if under the influence
of an attractive force in depth generated by the binocular feature. In ambiguous
cases the percept is often multi-stable, jumping back and forth in depth,
especially when monocular perspective cues conflict with the binocular disparity
information. The perceived depth of the monocularly specified surfaces is
measured psychophysically using a three-dimensional disparity-specified cursor,
whose depth is adjusted by the subject to match the depth of the perceived
surface at that point. Subjects report a curious interaction between the cursor
and the perceived surface, which is observed to flex in depth towards the cursor
at small disparity differences, in the manner of the attraction and repulsion in
depth reported by Westheimer & Levi (1987). This dynamic influence is
suggestive of a grouping by proximity mechanism, expressed as a field-like
attraction between perceived features in depth, and the flexing of the perceived
surface near the 3-D cursor, as well as the multistability in the presence of
conflicting perspective and disparity cues, are suggestive of a Gestalt Bubble
model. Carman & Welch (1992) employ a similar cursor to measure the perceived
depth of three-dimensional illusory surfaces seen in Kanizsa figure stereograms,
whose inducing edges are tilted in depth in a variety of configurations, as
shown in Figure 16 A. Note how the illusory surface completes in depth by
coplanar interpolation defining a smooth curving surface. The subjects in this
experiment also reported a flexing of the perceived surface in depth near the
disparity-defined cursor. Equally interesting is the "port hole" illusion seen
in the reverse-disparity version of this figure, where the circular completion
of the port holes generates an ambiguous unstable semi-transparent percept at
the center of the figure that is characteristic of the Gestalt Bubble model.
Kellman & Shipley (1991) and Idesawa (1991) report the emergence of more
complex illusory surfaces in depth, using similar illusory stereogram stimuli as
shown in Figure 16 B and C. It is difficult to deny the reality of a precise
high-resolution spatial interpolation mechanism in the face of these compelling
illusory percepts. Whatever the neurophysiological basis of these phenomena, the
Gestalt Bubble model offers a mathematical framework for a precise description
of the information encoded in these elaborate spatial percepts, independent of
the confounding factor of neurophysiological considerations.
The sophistication of the perceptual reification capacity is revealed by the
apparent motion phenomenon (Coren et al. 1994) which, in its simplest
form consists of a pair of alternately flashing lights, that generates a percept
of a single light moving back and forth between the flashing stimuli. With more
complex variations of the stimulus, the illusory percept is observed to change
color or shape in mid-flight, to carry illusory contours, or to carry a texture
region bounded by an illusory contour between the alternately flashing stimuli
(Coren et al. 1994). Most pertinent to the discussion of a spatial
representation is the fact that the illusory percept is observed to make
excursions into the third dimension when that produces a simpler percept. For
example if an obstacle is placed between the flashing stimuli so as to block the
path between them, the percept is observed to pass either in front of, or behind
the obstacle in depth. Similarly, if the two flashing stimuli are in the shape
of angular features like a "<" and ">" shape, this angle is observed to
rotate in depth between the flashing stimuli, preserving a percept of a rigid
rotation in depth, in preference to a morphological deformation in two
dimensions. The fact that the percept transitions so readily into depth suggests
the fundamental nature of the depth dimension for perception. While the apparent motion effects reify whole perceptual gestalts, the
elements of this reification, such as the field-like diffusion of perceived
surface properties, are seen in such diverse phenomena as the perceptual
filling-in of the Kanizsa figure (Takeichi et al. 1992), the
Craik-O'Brien-Cornsweet effect (Cornsweet 1970), the neon color spreading effect
(Bressan 1993), the filling-in of the blind spot (Ramachandran 1992), color
bleeding due to retinal stabilization (Heckenmuller 1965, Yarbus 1967), the
motion capture effect (Ramachandran & Anstis 1986), and the aperture problem
in motion perception (Movshon et al. 1986). In all of these phenomena, a
perceived surface property (brightness, transparency, color, motion, etc.) is
observed to spread from a localized origin, not into a fuzzy ill-defined region,
but rather, into a sharply bounded region containing a homogeneous perceptual
quality, and this filling-in occurs as readily in depth in a perspective view as
in the frontoparallel plane. The time has come to recognize that these phenomena
do not represent exceptional or special cases, nor are they illusory in the
sense of lacking a neurophysiological counterpart. Rather, these phenomena
reveal a general principle of neurocomputation that is ubiquitous in biological
vision. Evidence for the spherical nature of perceived space dates back to
observations by Helmholtz (1925). A subject in a dark room is presented with a
horizontal line of point-lights at eye level in the frontoparallel plane, and
instructed to adjust their displacement in depth, one by one, until they are
perceived to lie in a straight line in depth. The result is a line of lights
that curves inwards towards the observer, the amount of curvature being a
function of the distance of the line of lights from the observer. Helmholtz
recognized this phenomenon as evidence of the non-Euclidean nature of perceived
space. The Hillebrand-Blumenfeld alley experiments (Hillebrand 1902,
Blumenfeld 1913) extended this work with different configurations of lights, and
mathematical analysis of the results (Luneburg 1950, Blank 1958) characterized
the nature of perceived space as Riemannian with constant Gaussian curvature
(see Graham 1965, Foley 1978, and Indow 1991 for a review). In other words,
perceived space bows outward from the observer, with the greatest distortion
observed proximal to the body, as suggested by the Gestalt Bubble model. Heelan
(1983) presents a more modern formulation of the hyperbolic model of perceived
space, and provides further supporting evidence from art and illusion. It is perhaps too early to say definitively whether the model presented here
can be formulated to address all of the phenomena outlined above. What is
becoming increasingly clear however is the inadequacy of the conventional
feed-forward abstraction approach to account for these phenomena, and that
therefore novel and unconventional approaches to the problem should be given
serious consideration. The general solution offered by the Gestalt Bubble model
to all of these problems in perception is that the internal perceptual
representation encodes properties of the distal object rather than of the
proximal stimulus, that the computations of spatial perception are most easily
performed in a fully spatial matrix, in a manner consistent with the subjective
experience of perception. I have presented an elaborate model of perception that incorporates many of
the concepts and principles introduced by the original Gestalt movement. While
the actual mechanisms of the proposed model remain somewhat vague and poorly
specified, this is not a model that makes no predictions. Indeed this model,
even in its present general form makes the following very specific
predictions: These "predictions" are so immediately manifest in the subjective experience
of perception that they need hardly be tested psychophysically. And yet
curiously, these most obvious properties of perception have been systematically
ignored by neural modelers, even though the central significance of these
phenomena was highlighted decades ago by the Gestaltists. There are two reasons
why these prominent aspects of perception have been consistently ignored. The
first results from the outstanding success of the single-cell recording
technique, which has shifted our theoretical emphasis from field-like theories
of whole aspects of perception, to point-like theories of the elements of neural
computation. Like the classical Introspectionists, who refused to acknowledge
perceptual experiences that were inconsistent with their preconceived notions of
sensory representation, the Neuroreductionists of today refuse to consider
aspects of perception that are inconsistent with current theories of neural
computation, and some of them are even prepared to deny consciousness itself in
a heroic attempt to save the sinking paradigm. There is another factor that has made it possible to ignore these most
salient aspects of perception, which is that perceptual entities, such as the
solid volumes and empty spaces we perceive around us, are easily confused with
real objects and spaces in the objective external world. The illusion of
perception is so compelling that we mistake the percept of the world for the
real world itself. And yet this naïve realist view that we can somehow perceive
the world directly, is inconsistent with the physics of perception. If
perception is a consequence of neural processing of the sensory input, a percept
cannot in principle escape the confines of our head to appear in the world
around us, any more than a computation in a digital computer can escape the
confines of the computer. We cannot therefore in principle have direct
experience of objects in the world itself, but only of the internal effigies of
those objects generated by mental processes. The world we see around us
therefore can only be an elaborate, though very compelling illusion, which must
in reality correspond to perceptual data structures and processes occurring
actually within our own head. As soon as we examine the world we see around us,
not as a physical scientist observing the physical world, but as a
perceptual scientist observing a rich and complex internal percept,
only then does the rich spatial nature of perceptual processing become
immediately apparent. It was this central insight into the illusion of
consciousness that formed the key inspiration of the Gestalt movement, from
which all of their other ideas were developed. The central message of Gestalt
theory therefore is that the primary function of perceptual processing is the
generation of a miniature, virtual-reality replica of the external world inside
our head, and that the world we see around us is not the real external world,
but is exactly that miniature internal replica. It is only in this context that
the elaborate model presented here begins to seem plausible. Note for HTML version: If your browser does not load the "Symbol"
font, there will be problems with some of the following equations. Pi appears as
p, theta appears as q, alpha
appears as a, etc. If you see proper greek letters
here, this problem does not apply to you. The mathematical form of the coplanarity interaction field can be described
as follows. Consider the field strength F due to an element in the opaque
state at some point in the volume of the spatial matrix, with a certain surface
orientation, depicted in figure 17 A as a vector, representing the normal to the
surface encoded by that element. The strength of the field F should peak
within the plane at right angles to this normal vector (depicted as a circle in
figure 17 A) as defined in polar coordinates by the function Fa = sin(a),
where a is the angle between the surface normal
and some point in the field, that ranges from zero, parallel to the normal
vector, to p, in the opposite direction. The sine
function peaks at a = p/2, as shown in Figure 17 B,
producing an equatorial belt around the normal vector as suggested schematically
in cross-section in Figure 17 C, where the gray shading represents the strength
of the field. The strength of the field should actually decay with distance from
the element, for example with an exponential decay function, as defined by the
equation Far =
e-r2 sin(a) as shown in
Figure 17 D, where r is the radial distance from the element. This
produces a fading equatorial band, as suggested schematically in cross-section
in Figure 17 E. The equatorial belt of the function described so far would be
rather fat, resulting in a lax or fuzzy coplanarity constraint, but the
constraint can be stiffened by raising the sine to some positive power P,
producing the equation Far =
e-r2 sin(a)P which will produce a sharper peak in
the function as shown in Figure 17 F, producing a sharper in-plane field
depicted schematically in cross-section in Figure 17 G. In order to control
runaway positive feedback and suppress the uncontrolled proliferation of
surfaces, the field function should be normalized, in order to project
inhibition in directions outside the equatorial plane. This can be achieved with
the equation Far =
e-r2 2 sin(a)P - 1 which has the effect of shifting
the equatorial function half way into the negative region as shown in Figure 17
H, producing the field suggested in cross section in Figure 17 I.
The field described so far is un-oriented, i.e. it has a magnitude, but no
direction at any sample point (r,a). What is actually
required is a field with a direction, that would have maximal influence on
adjacent elements that are oriented parallel to it, i.e. elements that are
coplanar with it in both position and orientation. We can describe this
orientation of the field with the parameter q, that
represents the orientation at which the field F is sampled, expressed as
an angle relative to the normal vector; in other words, the strength of the
influence F exerted on an adjacent element located at a point
(r,a) varies with the deviation q of that element from the direction parallel to the normal
vector, as shown in Figure 18, such that the maximal influence is felt when the
two elements are parallel, i.e. when q = 0, as in
Figure 18 A, and falls off smoothly as the other element's orientation deviates
from that orientation as in Figure 18 B and C. This can be expressed with a
cosine function, such that the influence F of an element on another
element in a direction a and separation r from
the first element, and with a relative orientation q
would be defined by8.7 Bounding the Representation
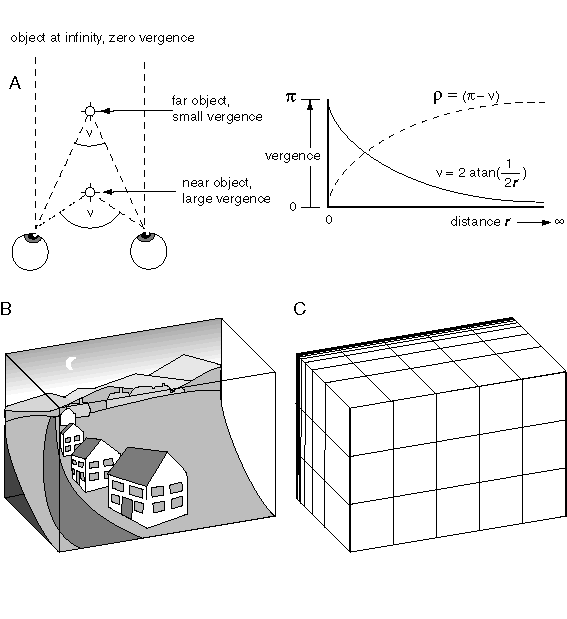
Figure 13
A: A vergence representation maps infinite distance into a finite range. B:
This produces a mapping reminiscent of a museum diarama. C: The compressed
reference grid in this compressed space defines intervals that are perceived to
be of uniform size.
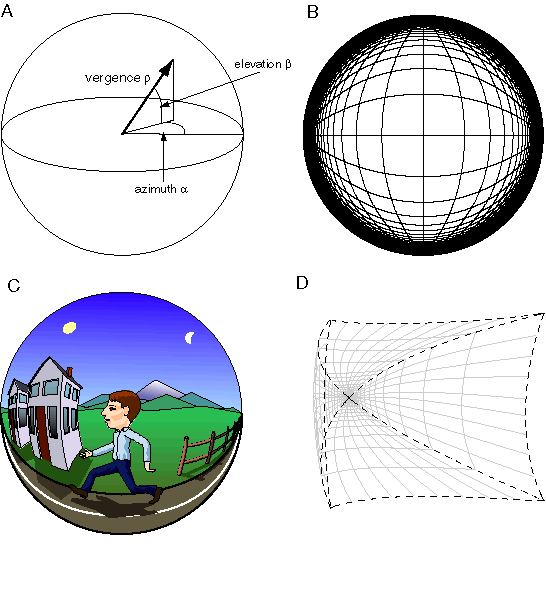
Figure 14
A: An azimuth / elevation / vergence representation maps the infinity of
three-dimensional Euclidean space into a finite perceptual space. B: The
deformation of the infinite Cartesian grid caused by the perspective
transformation of the azimuth / elevation / vergence representation. C: A view
of a man walking down a road represented in the perspective distorted space. D:
A section of the spherical space depicted in the same format as the perspective
space shown in figure 12.
8.8 Brain Anchoring
Figure 15
The image from the retina is projected into the perceptual sphere from the
center outward in the direction of gaze, as an inverse analog of the cone of
light that enters the eye in the external world, taking into account eye, head,
and body orientation in order to update the appropriate portion of perceptual
space.
9 Discussion
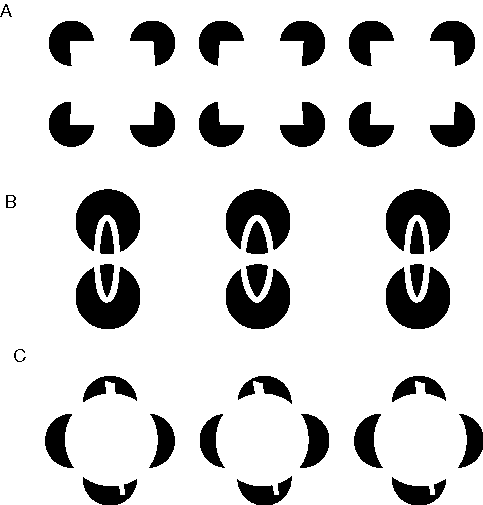
Figure 16
Perceptual interpolation in depth in illusory figure stereograms, adapted
from A: Carman et al. (1992), B: Kellman et al. (1991), and C: Idesawa (1991).
Opposite disparity percepts are achieved by binocular fusion of either the first
and second, or the second and third columns of the figure.
10 Conclusion
Appendix
The Coplanarity Field
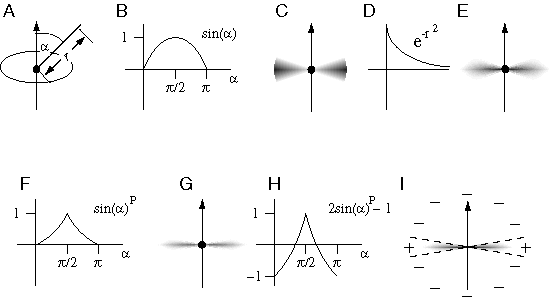
Figure 17
Progressive construction of the equation for the coplanarity field from one
element to another, as described in the text.
| Farq = e-r2 [2 sin(a)P - 1] | cos(q)Q | | (EQ 1) |
This cosine function allows the coplanar influence to propagate to near-coplanar orientations, thereby allowing surface completion to occur around smoothly curving surfaces. The tolerance to such curvature can also be varied parametrically by raising the cosine function to a positive power Q, as shown in Equation 1. So the in-plane stiffness of the coplanarity constraint is adjusted by parameter P, while the angular stiffness is adjusted by parameter Q. The absolute value on the cosine function in Equation 1 allows interaction between elements when q is between p/2 and p.
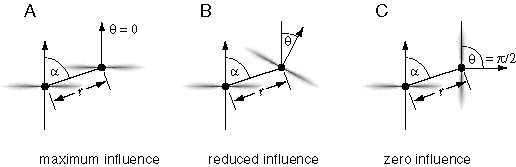
The orthogonality and occlusion fields have one less dimension of symmetry than the coplanarity field, and therefore they are defined with reference to two vectors through each element at right angles to each other, as shown in Figure 19 A. For the orthogonality field, these vectors represent the surface normals to the two orthogonal planes of the corner, while for the occlusion field one vector is a surface normal, and the other vector points within that plane in a direction orthogonal to the occlusion edge. The occlusion field G around the local element is defined in polar coordinates from these two vector directions, using the angles a and b respectively, as shown in Figure 19 A. The plane of the first surface is defined as for the coplanarity field, with the equation Gabr = e-r2 sin(a)P. For the occlusion field this planar function should be split in two, as shown in Figure 19 B to produce a positive and a negative half, so that this field will promote surface completion in one direction only, and will actually suppress surface completion in the negative half of the field. This can be achieved by multiplying the above equation by the sign (plus or minus, designated by the function sgn()) of a cosine on the orthogonal vector, i.e. Gabr = e-r2 sin(a)P sgn(cos(b)). Because of the negative half-field in this function, there is no need to normalize the equation. However the oriented component of the field can be added as before, resulting in the equation
| Gabrq = e-r2 [sin(a)P sgn(cos(b))] | cos(q)Q | | (EQ 2) |
Again, the maximal influence will be experienced when the two elements are parallel in orientation, i.e. when q = 0. As before, the orientation cosine function is raised to the positive power Q, to allow parametric adjustment of the stiffness of the coplanarity constraint.
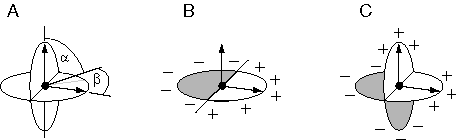
The orthogonality field H can be developed in a similar manner, beginning with the planar function divided into positive and negative half-fields, i.e. with the equation Habr = e-r2 sin(a)P sgn(cos(b)) but then adding another similar plane from the orthogonal surface normal, producing the equation Habr = e-r2 [sin(a)P sgn(cos(b)) + sin(b)P sgn(cos(a))]. This produces two orthogonal planes, each with a negative half-field, as shown schematically in Figure 19 C. Finally, this equation must be modified to add the oriented component to the field, represented by the vector q, such that the maximal influence on an adjacent element will be experienced when that element is either within one positive half-plane and at one orientation, or is within the other positive half-plane and at the orthogonal orientation. The final equation for the orthogonality field therefore is defined by
| Habrq = e-r2 [sin(a)P sgn(cos(b)) | cos(q)Q | + [sin(b)P sgn(cos(a)) | cos(q)Q |] | (EQ 3) |
There is another aspect of the field-like interaction between elements that remains to be defined. Both the orthogonal and the occlusion states are promoted by appropriately aligned neighboring elements in the coplanar state. Orthogonal and occlusion elements should also feel the influence of neighboring elements in the orthogonal and occlusion states, because a single edge should have a tendency to become either an orthogonal corner percept, or an occlusion edge percept along its entire length. Therefore orthogonal or occlusion elements should promote like-states, and inhibit unlike-states in adjacent elements along the same corner or edge. The interaction between like-state elements along the edge will be called the edge-consistency constraint, and the corresponding field of influence will be designated E, while the complementary interaction between unlike-state elements along the edge is called the edge-inconsistency constraint, whose corresponding edge-inconsistency field will be designated I. These interactions are depicted schematically in Figure 20
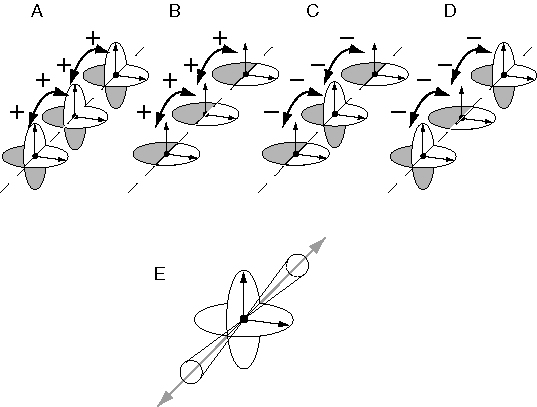
The spatial direction along the edge can be defined by the product of the two sine functions sin(a) sin(b) defining the orthogonal planes, denoting the zone of intersection of those two orthogonal planes, as suggested in Figure 20 E. Again, this field can be sharpened by raising these sine functions to a positive power P, and localized by applying the exponential decay function. The edge consistency constraint E therefore has the form Eabr = e-r2 [sin(a)P sin(b)P]. As for the orientation of the edge-consistency field, this will depend now on two angles,q and f, representing the orientations of the two orthogonal vectors of the adjacent orthogonal or occlusion elements relative to the two normal vectors respectively. Both the edge-consistency and the edge-inconsistency fields, whether excitatory between like-state elements, or inhibitory between unlike-state elements, should peak when both pairs of reference vectors are parallel to the normal vectors of the central element, i.e. when q and f are both equal to zero. The full equation for the edge-consistency field E would therefore be
| Eabrqf = e-r2 [sin(a)P sin(b)P] cos(q)Q cos(f)Q | (EQ 4) |
where this equation is applied only to like-state edge or corner elements, while the edge-inconsistency field I would be given by
| Iabrqf = e-r2 [sin(a)P sin(b)P] cos(q)Q cos(f)Q | (EQ 5) |
applied only to unlike-state elements. The total influence R on an occlusion element therefore is calculated as the sum of the influence of neighboring coplanar, orthogonal, and occlusion state elements as defined by
| Rabrqf = Gabrqf + Eabrqf - Iabrqf | (EQ 6) |
and the total influence S on an orthogonal state element is defined by
| Sabrqf = Habrqf + Eabrqf - Iabrqf | (EQ 7) |
A two-dimensional visual edge has an influence on the three-dimensional interpretation of a scene, since an edge is suggestive of either a corner or an occlusion at some orientation in three dimensions whose two-dimensional projection coincides with that visual edge. This influence however is quite different from the local field-like influences described above, because the influence of a visual edge should penetrate the volumetric matrix with a planar field of influence to all depths, and should activate all local elements within the plane of influence that are consistent with that edge. Subsequent local interactions between those activated elements serves to select which subset of them should finally represent the three-dimensional percept corresponding to the two-dimensional image. For example, a vertical edge as shown in Figure 21 A would project a vertical plane of influence, as suggested by the light shading in Figure 21 A, into the depth dimension of the volumetric matrix, where it stimulates the orthogonal and occlusion states which are consistent with that visual edge. For example it would stimulate corner and occlusion states at all angles about a vertical axis, as shown in Figure 21 A, where the circular disks represent different orientations of the positive half-fields of either corner or occlusion fields. However a vertical edge would also be consistent with corners or occlusions about axes tilted relative to the image plane but within the plane of influence, for example about the axes depicted in Figure 21 B. The same kind of stimulation would occur at every point within the plane of influence of the edge, although only one point is depicted in the figure. When all elements consistent with this vertical edge have been stimulated, the local field-like interactions between adjacent stimulated elements will tend to select one edge or corner at some depth and at some tilt, thereby suppressing alternative edge percepts at that two-dimensional location at different depths and at different tilts. At equilibrium, some arbitrary edge or corner percept will emerge within the plane of influence as suggested in Figure 21 C, which depicts only one such possible percept, while edge consistency interactions will promote like-state elements along that edge, producing a single emergent percept consistent with the visual edge. In the absence of additional influences, for example in the isolated local case depicted in Figure 21 C, the actual edge that emerges will be unstable, i.e. it could appear anywhere within the plane of influence of the visual edge through a range of tilt angles, and could appear as either an occlusion or a corner edge. However when it does appear, it propagates its own field-like influence into the volumetric matrix, in this example the corner percept would propagate a planar percept of two orthogonal surfaces that will expand into the volume of the matrix, as suggested by the arrows in Figure 21 C. The final percept therefore will be influenced by the global pattern of activity, i.e. the final percept will construct a self-consistent perceptual whole, whose individual parts reinforce each other by mutual activation by way of the local interaction fields, although that percept would remain unstable in all unconstrained dimensions. For example the corner percept depicted in Figure 21 C would snake back and forth unstably within the plane of influence, rotate back and forth along its axis through a small angle, and flip alternately between the corner and occlusion states, unless the percept is stabilized by other features at more remote locations in the matrix.
Anstis S. & Howard I, (1978) A Craik-O'Brien-Cornsweet Illusion for Visual Depth. Vision Research 18 213-217.
Arnheim R. (1969) Art and Visual Perception: A Psychology of the Creative Eye. Berkeley, University of California Press.
Attneave F. (1971) Multistability in Perception. Scientific American 225 142-151.
Attneave F. (1982) Prägnanz and soap bubble systems: a theoretical exploration. in Organization and Representation in Perception, J. Beck (Ed.), Hillsdale NJ, Erlbaum.
Baldwin T. (1992) The Projective Theory of Sensory Content. In: T. Crane (Ed.) The Contents of Experience: Essays on Perception. Cambridge UK: Cambridge University Press, 177-195.
Barlow H., Blakemore C., & Pettigrew J. (1967) The Neural Mechanism of Binocular Depth Discrimination. Journal of Physiology 193 327-342.
Barrow H. G. & Tenenbaum J. M. (1981) Interpreting Line Drawings as Three Dimensional Surfaces. Artificial Intelligence 17, 75-116.
Bisiach E. & Luzatti C. (1978) Unilateral Neglect of Representational Space. Cortex 14 129-133.
Bisiach E., Capitani E., Luzatti C., & Perani D. (1981) Brain and Conscious Representation of Outside Reality. Neuropsychologia 19 543-552.
Blank A. A. (1958) Analysis of Experiments in Binocular Space Perception. Journal of the Optical Society of America, 48 911-925.
Blumenfeld W. (1913) Untersuchungen Über die Scheinbare Grösse im Sehraume. Zeitschrift für Psychologie 65 241-404.
Boring (1933) The Physical Dimensions of Consciousness. New York: Century.
Bressan P. (1993) Neon colour spreading with and without its figural prerequisites. Perception 22 353-361
Brookes A. & Stevens K. (1989) The analogy between stereo depth and brightness. Perception 18 601-614.
Bruce V. & Green P. (1987) Visual Perception: Physiology, psychology, and ecology. Hillsdale NJ: Erlbaum.
Carman G. J., & Welch L. (1992) Three-Dimensional Illusory Contours and Surfaces. Nature 360 585-587.
Chalmers, D. J. (1995) Facing Up to the Problems of Consciousness. Journal of Consciousness Studies 2 (3) 200-219. Reprinted in "Toward a Science of Consciousness II, The Second Tucson Discussions and Debates". (1996) S. R. Hameroff, A. W. Kaszniak, & A. C. Scott (Eds.) 5-28.
Charnwood J. R. B. (1951) Essay on Binocular Vision. London, Halton Press.
Collett T. (1985) Extrapolating and Interpolating Surfaces in Depth. Proc. R. Soc. Lond. B 224 43-56.
Coren S., Ward L. M., & Enns J. J. (1979) Sensation and Perception. Ft Worth TX, Harcourt Brace.
Cornsweet T. N. (1970) Visual Perception. New York, Academic Press.
Crick F. & Koch C. (1990) Toward a Neurobiological Theory of Consciousness. Seminars in the Neurosciences 2: 263-275.
Crick F. (1994) The Astonishing Hypothesis: The Scientific Search for the Soul. New York: Scribners.
Dennett D. (1991) Consciousness Explained. Boston, Little Brown & Co.
Dennett D. (1992) `Filling In' Versus Finding Out: a ubiquitous confusion in cognitive science. In Cognition: Conceptual and Methodological Issues, Eds. H. L. Pick, Jr., P. van den Broek, & D. C. Knill. Washington DC.: American Psychological Association.
Earle D. C. (1998) On the Roles of Consciousness and Representations in Visual Science. Behavioral & Brain Sciences 21 (6), pp 757-758, commentary on Pessoa et al. (1998).
Eckhorn R., Bauer R., Jordan W., Brosch M., Kruse W., Munk M., Reitboeck J. (1988) Coherent Oscillations: A Mechanism of Feature Linking in the Visual Cortex? Biol. Cybern. 60 121-130.
Foley J. M. (1978) Primary Distance Perception.In: Handbook of Sensory Physiology, Vol VII Perception. R. Held, H. W. Leibowitz, & HJ. L. Tauber (Eds.) Berlin: Springer Verlag, pp 181-213.
Gibson J. J. (1972) A Theory of Direct Visual Perception. In: The Psychology of Knowing. (J. R. Royce & W. W. Rozeboom (Eds.), Gordon & Breach.
Gibson J. J. (1979) The Ecological Approach to Visual Perception. Houghton Mifflin.
Gibson J. J. & Crooks L. E. (1938) A Theoretical Field-Analysis of Automobile Driving. The American Journal of Psycholgy 51 (3) 453-471.
Gillam B. (1971) A Depth Processing Theory of the Poggendorf Illusion. Perception & Psychophysics 10, 211-216.
Gillam, B. (1980) Geometrical Illusions. Scientific American 242 102-111.
Graham C. H. (1965) Visual Space Perception. in C. H. Graham (Ed.) Vision and Visual Perception, New York, John Wiley 504-547.
Green M. & Odum V. J. (1986) Correspondence Matching in Apparent Motion: Evidence for Three Dimensional Spatial Representation. Science 233 1427-1429.
Gregory R. L. (1963) Distortion of Visual Space as Inappropriate Constancy Scaling. Nature 199, 678-679.
Grossberg S, Mingolla E, (1985) "Neural Dynamics of Form Perception: Boundary Completion, Illusory Figures, and Neon Color Spreading" Psychological Review 92 173-211.
Grossberg S, Todorovic D, (1988) "Neural Dynamics of 1-D and 2-D Brightness Perception: A Unified Model of Classical and Recent Phenomena" Perception and Psychophysics 43, 241-277.
Harrison S. (1989) A New Visualization on the Mind-Brain Problem: Naive Realism Transcended. In J. Smythies & J. Beloff (Eds.) The Case for Dualism. Charlottesville: University of Virginia.
Heckenmuller E. G. (1965) Stabilization of the Retinal Image: A Review of Method, Effects, and Theory. Psychological Bulletin 63 157-169.
Heelan P. A. (1983) Space Perception and the Philosophy of Science. Berkeley. University of California Press.
Helmholtz H. (1925) Physiological Optics. Optical Society of America 3 318.
Hillebrand F. (1902) Theorie der Scheinbaren Grösse bei Binocularem Sehen. Denkschr. Acad. Wiss. Wien (Math. Nat. Kl.), 72 255-307.
Hochberg J. & Brooks V. (1960) The Psychophysics of Form: Reversible Perspective Drawings of Spatial Objects. American Journal of Psychology 73 337-354.
Hoffman D. D. (1998) Visual Intelligence: How We Create What We See. New York: W. W. Norton.
Idesawa M. (1991) Perception of Illusory Solid Object with Binocular Viewing. Proceedings IJCNN
Indow T. (1991) A Critical Review of Luneberg's Model with Regard to Global Structure of Visual Space. Psychological Review 98, 430-453.
Julesz B. (1971) Foundations of Cyclopean Perception. Chicago, University of Chicago Press.
Kanizsa G, (1979) Organization in Vision. New York, Praeger.
Kant I. (1781 / 1991) Critique of Pure Reason. Vasilis Politis (Ed.) London: Dent.
Kaufman (1974) Sight and Mind. New York, Oxford University Press.
Kellman P. J., & Shipley T. F. (1991) A Theory of Visual Interpolation in Object Perception. Cognitive Psychology 23 141-221.
Kellman P. J., Machado L. J., Shipley T. F., & Li C. C. (1996) Three-Dimensional Determinants of Object Completion. Annual Review of Vision and Ophthalmology (ARVO) abstracts, 3133 37 (3) p. S685.
Koffka K, (1935) Principles of Gestalt Psychology. New York, Harcourt Brace & Co.
Köhler W. & Held R. (1947) The Cortical Correlate of Pattern Vision. Science 110: 414-419.
Köhler W. (1969) The Task of Gestalt Psychology. Princeton NY. Princeton University Press.
Köhler W. (1971) A Task For Philosophers. In: The Selected Papers of Wolfgang Koehler, Mary Henle (Ed.) Liveright, New York. pp 83-107.
Kolb B. & Whishaw I. Q. (1996) Fundamentals of Human Neuropsychology. W. H. Freeman, p. 247-276.
Kosslyn S. M. (1975) Information Representation in Visual Images. Cognitive Psychology 7 341-370.
Kosslyn S. M. (1980) Image and Mind. Cambridge MA, Harvard University Press.
Kosslyn S. M. (1994) Image and Brain: The Resolution of the Imagery Debate. Cambridge MA, MIT Press.
Kuhn T. S. (1970) The Structure of Scientific Revolutions. Chicago: Chicago University Press.
Lesher G. W. (1995) Illusory Contours: Toward a Neurally Based Perceptual Theory. Psychonomic Bulletin and Review 2:279-321.
Llinas R. R., Ribary U., Joliot M., & Wang X. -J (1994) Content and Context in Temporal Thalamocortical Binding. In G. Buzsaki, R. R. Llinas, & W. Singer (Eds.) Temporal Coding in the Brain. Berlin: Springer-Verlag.
Luneburg R. K. (1950) The Metric of Binocular Visual Space. Journal of the Optical Society of America, 40 627-642.
Marr D. & Poggio T. (1976) Cooperative Computation of Stereo Disparity. Science 194 283-287.
Mitchison G, (1993) The neural representation of stereoscopic depth contrast. Perception 22 1415-1426
Movshon J. A., Adelson E. H., Gizzi M. S., & Newsome W. T. (1986) The Analysis of Moving Patterns. In C. Chagas, R. Gattass, & C. Cross (Eds.) Pattern Recognition Mechanisms, 112-151. Berlin: Springer Verlag.
Müller G. E. (1896) Zur Psychophysik der Gesichtsempfindungen. Zeitschrift für Psychologie 10.
Nagel T. (1974) What Is It Like to Be a Bat? Philosophical Review 83 435-450
O'Regan K. J., (1992) Solving the `Real' Mysteries of Visual Perception: The World as an Outside Memory. Canadian Journal of Psychology 46 461-488.
O'Shaughnessy B. (1980) The Will: A Dual Aspect Theory. (2 volumes) Cambridge UK: Cambridge University Press.
Pessoa L., Thompson E., & Noë A. (1998) Finding Out About Filling-In: A guide to perceptual completion for visual science and the philosophy of perception. Behavioral and Brain Sciences 21, 723-802.
Pinker S. (1980) Mental Imagery and the Third Dimension. Journal of Experimental Psychology 109 354-371.
Pinker S. (1988) A Computational Theory of the Mental Imagery Medium. In: M. Denis, J. Engelkamp, J. T. E. Richardson (Eds.) Cognitive and Neuropsychological Approaches to Mental Imagery. Boston, Martinus Nijhoff.
Price H. H. (1932) Perception. London: Methuen & Co. Ltd.
Ramachandran V. S. & Anstis S. M. (1986) The Perception of Apparent Motion. Scientific American 254 80-87.
Ramachandran V. S. (1992) Filling in Gaps in Perception: Part 1 Current Directions in Psychological Science 1 (6) 199-205
Revonsuo A. (1995) Consciousness, Dreams, and Virtual Realities. Philosophical Psychology 8 (1) 35-58.
Revonsuo A. (1998) Visual Perception and Subjective Visual Awareness. Open peer commentary to Pessoa et al. (1998) pp 769-770.
Rock I, & Brosgole L. (1964) Grouping Based on Phenomenal Proximity. Journal of Experimental Psychology 67 531-538.
Ruch (1950) In J. F. Fulton (Ed.) Textbook of Physiology, 16th Ed. Philadelphia, p. 311. Pertinent passage quoted in Smythies (1954).
Russell B. (1927) Philosophy. New York: W. W. Norton.
Sacks, O. (1985) The Man Who Mistook His Wife For a Hat. New York, Harper & Row. p. 77-79
Searle J. R. (1992) The Rediscovery of Mind. Cambridge MA: The MIT Press.
Shannon C. E. (1948) A Mathematical Theory of Communication. Bell Systems Technical Journal 27: 379-423.
Shepard R. N. & Metzler J. (1971) Mental Rotation of Three-Dimensional Objects. Science 171 701-703.
Singh M. & Hoffman D. D. (1998) Active Vision and the Basketball Problem. Behavioral & Brain Sciences 21 (6), pp 772-773, commentary on Pessoa et al. (1998).
Smythies J. R. (1954) Analysis of Projection. British Journal for the Philosophy of Science 5, 120-133.
Smythies J. R. (1989) The Mind-Brain Problem. In: J. R. Smythies & J. Beloff (Eds) The Case For Dualism. Charlottesville: University of Virginia Press.
Smythies J. R. (1994) The Walls of Plato's Cave: the science and philosophy of brain, consciousness, , and perception. Aldershot UK: Avebury.
Takeichi H, Watanabe T, Shimojo S, (1992) Illusory occluding contours and surface formation by depth propagation. Perception 21 177-184
Tausch, R. (1954) Optische Täyschungen als artifizielle Effekte der Gestaltungs-prozesse von Grössen und Formenkonstanz in der natürlichen Raumwahrnehmung. Psychologische Forschung, 24, 299-348.
Tse P. U. (1999a) Illusory Volumes from Conformation. Perception (in press).
Tse P. U. (1999b) Volume Completion. Cognitive Psychology (submitted)
Velmans M. (1990) Consciousness, Brain and the Physical World. Philosophical Psychology 3 (1) 77-99.
Ware C. & Kennedy J. M. (1978) Perception of Subjective Lines, Surfaces and Volumes in 3-Dimensional Constructions. Leonardo 11 111-114.
Westheimer G. & Levi D. M. (1987) Depth Attraction and Repulsion of Disparate Foveal Stimuli. Vision Research 27 (8) 1361-1368.
Yarbus A. L. (1967) Eye Movements and Vision. New York: Plenum Press.
Zucker S. W., David C., Dobbins A., & Iverson L. 1988 "The Organization of Curve Detection: Coarse Tangent Fields and Fine Spline Coverings". Proceedings: Second International Conference on Computer Vision, IEEE Computer Society, Tampa FL 568-577.