Modèles probabilistes pour les architectures profondes¶
On s’intéresse particulièrement au modèle de la machine de Boltzmann, dont certaines variantes sont utilisées dans des architectures profondes comme les Deep Belief Networks et les Deep Boltzmann Machines. Voir la section 5 de Learning Deep Architectures for AI.
La distribution de Boltzmann est généralement sur des variables binaires 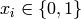 , avec
, avec
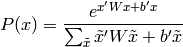
où le dénominateur est simplement un facteur de normalisation pour que 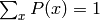 ,
et les
,
et les 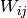 indiquent la nature de l’interaction (e.g. positive =
indiquent la nature de l’interaction (e.g. positive = 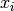 et
et 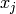 veulent prendre la même valeur) entre les paires de variables, et
veulent prendre la même valeur) entre les paires de variables, et 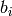 indique la propension de
indique la propension de 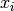 à prendre la valeur 1.
à prendre la valeur 1.
Rappels sur les modèles graphiques probabilistes¶
Voir
Graphical models: probabilistic inference. M. I. Jordan and Y. Weiss. In M. Arbib (Ed.), The Handbook of Brain Theory and Neural Networks, 2nd edition. Cambridge, MA: MIT Press, 2002.
On peut écrire certaines distributions 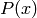 pour un
vecteur de variables
pour un
vecteur de variables 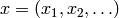 sous la forme
sous la forme
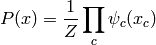
où 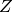 est le facteur de normalisation (appelée fonction de partition),
et la somme est sur des cliques (des sous-ensembles
est le facteur de normalisation (appelée fonction de partition),
et la somme est sur des cliques (des sous-ensembles 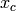 des éléments du vecteur
des éléments du vecteur 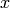 ),
et les
),
et les 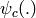 sont des fonctions (une par clique) qui indiquent comment
intéragissent les variables de chaque clique.
sont des fonctions (une par clique) qui indiquent comment
intéragissent les variables de chaque clique.
Un cas particulier où 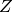 peut-être simplifié un
peu (factorisé sur les cliques) est celui des modèles dirigés où les variables
sont structurées dans un graphe dirigé acyclique, avec un ordre topologique
associant un ensemble de parents
peut-être simplifié un
peu (factorisé sur les cliques) est celui des modèles dirigés où les variables
sont structurées dans un graphe dirigé acyclique, avec un ordre topologique
associant un ensemble de parents 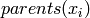 à chaque
variable
à chaque
variable 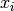 :
:
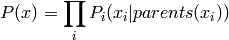
où donc on voit qu’il y a une clique pour chaque variable et ses parents,
i.e., 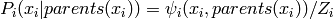 .
.
Dans le cas général (représenté avec un graphe non-dirigé), les
fonctions de potentiel 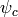 sont directement paramétrisées,
souvent dans l’espace du logarithme de
sont directement paramétrisées,
souvent dans l’espace du logarithme de 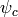 , ce qui
donne lieu à la formulation appelée champs aléatoire de Markov:
, ce qui
donne lieu à la formulation appelée champs aléatoire de Markov:
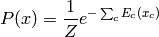
où 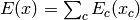 , comme fonction de
, comme fonction de 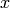 ,
est appelée fonction d’énergie. La fonction d’énergie
de la machine de Boltzmann est donc un polynôme du second
degré en
,
est appelée fonction d’énergie. La fonction d’énergie
de la machine de Boltzmann est donc un polynôme du second
degré en 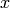 . La paramétrisation la plus
commune des champs aléatoires de Markov a la forme suivante,
qui est log-linéaire:
. La paramétrisation la plus
commune des champs aléatoires de Markov a la forme suivante,
qui est log-linéaire:
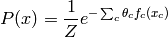
où les seuls paramètres libres sont les 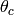 ,
et où donc la log-vraisemblance complète (quand
,
et où donc la log-vraisemblance complète (quand 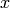 est complètement observé dans chaque exemple) est log-linéaire
en les paramètres
est complètement observé dans chaque exemple) est log-linéaire
en les paramètres 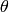 , et on peut facilement
montrer qu’elle est convexe en
, et on peut facilement
montrer qu’elle est convexe en 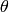 .
.
Inférence¶
Un des obstacles les plus importants à l’application pratique
de la plupart des modèles probabilistes est l’inférence:
étant données certaines variables (un sous-ensemble de 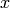 ),
prédire la distribution marginale (chacune séparément) ou jointe
de certaines autres. Soit
),
prédire la distribution marginale (chacune séparément) ou jointe
de certaines autres. Soit 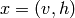 avec
avec 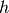 (hidden)
les variables non-observées que l’on veut prédire, et
(hidden)
les variables non-observées que l’on veut prédire, et  (visible)
la partie observée. On voudrait calculer ou tout au moins
échantillonner de
(visible)
la partie observée. On voudrait calculer ou tout au moins
échantillonner de
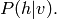
L’inférence est évidemment utile si certaines des variables sont manquantes, ou simplement si pendant l’utilisation du modèle, on veuille prédire une variable (par exemple la classe de l’image) étant donnée d’autres (par exemple l’image). Notons que si le modèle a des variables cachées (jamais observées dans les données) qu’on ne cherche pas à prédire directement, on devra quand même implicitement marginaliser sur ces variables (sommer sur toutes les configurations de ces variables).
L’inférence est aussi une composante essentielle de l’apprentissage, soit pour calculer un gradient directement (voir ci-bas le cas de la machine de Boltzmann), soit parce qu’on utilise l’algorithme E-M (Expectation-Maximization), qui requière une marginalisation sur toutes les variables cachées.
En général, l’inférence exacte a un coût de calcul exponentiel dans la taille des cliques du graphe (en fait de la partie non-observée du graphe), car on doit considérer toutes les combinaisons possibles des valeurs des variables dans chaque clique. Voir la section 3.4 de Graphical models: probabilistic inference pour un survol des méthodes exactes d’inférence.
Une forme simplifiée d’inférence consiste à trouver non pas toute la distribution mais seulement le mode (la configuation de valeurs la plus probable) de la distribution:
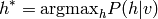
En anglais on appelle cela l’inférence MAP = Maximum A Posteriori.
Inférence approximative¶
Les deux familles principales d’inférence approximative pour les modèles probabilistes sont l’inférence par MCMC (chaîne de Markov Monte-Carlo) et l’inférence variationnelle.
Le principe de l’inférence variationnelle est le suivant. On va définir un modèle plus simple que le modèle cible (celui qui nous intéresse), dans lequel l’inférence sera facile, avec un jeu de variables semblables (mais généralement avec des dépendances plus simples entre elles que dans le modèle cible). On va ensuite optimiser les paramètres du modèle simple de façon à ce qu’il s’approche le plus possible du modèle cible. On va finalement faire l’inférence en utilisant le modèle simple. Voir la section 4.2 de Graphical models: probabilistic inference pour plus de détails et un survol.
Inférence par MCMC¶
En général, la loi 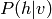 peut être exponentiellement chère à représenter (en terme du nombre
de variables cachées, car il faut considérer toutes les configurations
des
peut être exponentiellement chère à représenter (en terme du nombre
de variables cachées, car il faut considérer toutes les configurations
des 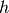 ).
Le principe de l’inférence par Monte-Carlo est que l’on va
approximer la distribution
).
Le principe de l’inférence par Monte-Carlo est que l’on va
approximer la distribution 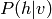 par des échantillons tirés de cette loi. En effet, en pratique
on a seulement besoin de faire une espérance (par exemple l’espérance
du gradient) sous cette loi conditionnelle. On va donc remplacer
l’espérance recherchée par une moyenne sur ces échantillons.
Voir la page du site du zéro sur Monte-Carlo
pour une introduction en douceur.
par des échantillons tirés de cette loi. En effet, en pratique
on a seulement besoin de faire une espérance (par exemple l’espérance
du gradient) sous cette loi conditionnelle. On va donc remplacer
l’espérance recherchée par une moyenne sur ces échantillons.
Voir la page du site du zéro sur Monte-Carlo
pour une introduction en douceur.
Malheureusement, pour la plupart des modèles probabilistes,
même tirer de 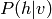 de manière
exacte n’est pas faisable facilement (en un temps de calcul
qui n’est pas exponentiel dans la dimension de
de manière
exacte n’est pas faisable facilement (en un temps de calcul
qui n’est pas exponentiel dans la dimension de 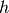 ).
C’est pourquoi l’approche la plus générale est basée sur
une approximation de l’échantillonage Monte-Carlo,
appelé Chaîne de Markov Monte-Carlo (MCMC en anglais).
).
C’est pourquoi l’approche la plus générale est basée sur
une approximation de l’échantillonage Monte-Carlo,
appelé Chaîne de Markov Monte-Carlo (MCMC en anglais).
Une chaîne de Markov (d’ordre 1) est
une suite de variables aléatoires 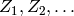 , telle que
, telle que
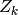 est indépendente de
est indépendente de 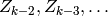 étant donnée
étant donnée 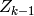 :
:
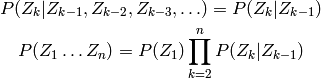
Le principe du tirage MCMC est que l’on va construire une
chaîne de Markov dont la distribution marginale asymptotique,
i.e., la loi de 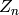 , quand
, quand 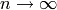 ,
converge vers une distribution cible, telle que
,
converge vers une distribution cible, telle que
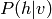 ou
ou 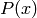 .
.
Échantillonage de Gibbs¶
Il existe de nombreuses méthodes d’échantillonage MCMC. Celle la plus couramment utilisée pour les architectures profondes est la méthode d’échantillonage de Gibbs (Gibbs sampling). Elle est simple et présente une certaine analogie avec le fonctionnement plausible du cerveau, où chaque neurone décide d’envoyer des impulsions avec un certain aléa, en fonction des impulsions qu’il reçoit d’autres neurones.
Supposons que l’on veuille échantillonner de la loi 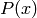 où
où 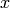 est un groupe de variables
est un groupe de variables 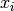 (et optionnellement on pourrait avoir des variables conditionnantes,
mais elles ne changent rien à la procédure à part de conditionner
tout, donc nous les ignorons dans la notation ici).
On notera
(et optionnellement on pourrait avoir des variables conditionnantes,
mais elles ne changent rien à la procédure à part de conditionner
tout, donc nous les ignorons dans la notation ici).
On notera 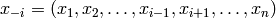 ,
soit toutes les variables de
,
soit toutes les variables de 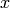 sauf
sauf 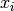 .
L’échantillonage de Gibbs ordinaire est donné par l’algorithme suivant:
.
L’échantillonage de Gibbs ordinaire est donné par l’algorithme suivant:
- Choisir un
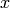 initial de manière arbitraire (aléatoire ou pas)
initial de manière arbitraire (aléatoire ou pas) - Pour chaque pas de la chaîne de Markov
- Itérer sur chaque
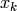 dans
dans 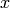
- Tirer
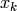 de la loi conditionnelle
de la loi conditionnelle 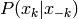
- Tirer
- Itérer sur chaque
Dans certains cas on peut regrouper les variables dans 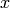 en blocs ou groupes de variables tels que tirer d’un groupe étant donnés les autres
est facile. Dans ce cas il est avantageux d’interpréter l’algorithme
ci-haut avec
en blocs ou groupes de variables tels que tirer d’un groupe étant donnés les autres
est facile. Dans ce cas il est avantageux d’interpréter l’algorithme
ci-haut avec 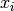 le i-eme groupe plutôt que la i-eme
variable. On appelle cela l’échantillonage de Gibbs par blocs.
le i-eme groupe plutôt que la i-eme
variable. On appelle cela l’échantillonage de Gibbs par blocs.
Le Gradient dans un Champs de Markov Log-Linéaire¶
Voir Learning Deep Architectures for AI pour les dérivations en détail.
Les champs de Markov log-linéaires sont des modèles probabilistes non-dirigés
où la fonction d’énergie est linéaire en terme des paramètres
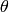 du modèle:
du modèle:
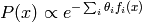
où les 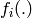 sont appelées les statistiques suffisantes
du modèles car les espérances
sont appelées les statistiques suffisantes
du modèles car les espérances ![E[f_i(x)]](_images/math/3eba7a57afb4739b629719623a47a16ec9472f85.png) sont suffisantes
pour caractériser la distribution et estimer les paramètres.
Notons que
sont suffisantes
pour caractériser la distribution et estimer les paramètres.
Notons que 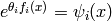 est
associé à chaque clique du modèle (en général seulement
un sous-vecteur de
est
associé à chaque clique du modèle (en général seulement
un sous-vecteur de 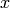 influence
influence 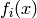 ).
).
Revenons au statistiques suffisantes. On peut montrer que le gradient de la log-vraisemblance se développe ainsi:
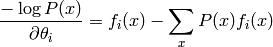
et le gradient moyen sur les exemples d’apprentissage 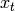 est donc
est donc
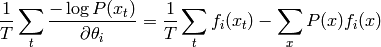
On voit donc que le gradient est annullé quand la moyenne des statistiques suffisantes sur la distribution d’apprentissage égale leur espérance sur le modèle P.
Malheureusement, même calculer le gradient est difficile.
On ne veut pas sommer sur tous les 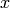 possibles, mais
heureusement, on peut obtenir une approximation Monte-Carlo
en faisant un ou plusieurs tirages de
possibles, mais
heureusement, on peut obtenir une approximation Monte-Carlo
en faisant un ou plusieurs tirages de 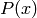 , ce qui
donne un gradient stochastique. En général, cependant, même
faire un tirage sans biais de
, ce qui
donne un gradient stochastique. En général, cependant, même
faire un tirage sans biais de 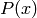 est exponentiellement
coûteux, et on utilise donc une méthode MCMC.
est exponentiellement
coûteux, et on utilise donc une méthode MCMC.
On appelle ‘partie positive’ la partie du gradient
dûe au numérateur de la probabilité (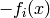 ),
et ‘partie négative’ la partie correspondant au gradient
de la fonction de partition (le dénominateur).
),
et ‘partie négative’ la partie correspondant au gradient
de la fonction de partition (le dénominateur).
Marginalisation sur les variables cachées¶
Quand certaines variables sont cachées, le gradient devient
un peu plus compliqué car il faut marginaliser sur les
variables cachées. Soit 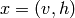 , avec
, avec  la partie visible
et
la partie visible
et 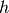 la partie cachée, avec les statistiques
des fonctions des deux,
la partie cachée, avec les statistiques
des fonctions des deux, 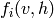 . Le gradient
moyen de la moins log-vraisemblance des données
observées devient
. Le gradient
moyen de la moins log-vraisemblance des données
observées devient
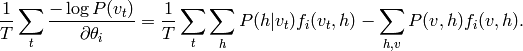
Il faudra donc dans ce cas généralement se résoudre à du MCMC
non seulement pour la partie négative mais aussi pour la partie
négative, pour échantillonner 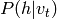 .
.
La Machine de Boltzmann¶
La machine de Boltzmann est un modèle probabiliste non-dirigé, une forme particulière de champs de Markov log-linéaire dans laquelle certaines variables sont observées (parfois) et d’autres ne le sont jamais (les variables cachées), et où la fonction d’énergie est un polynôme du second degré par rapport aux variables:
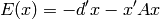
La machine de Boltzmann classique a des variables binaires
et l’inférence est faite par une MCMC de Gibbs, ce qui nécessite
de faire des tirages de 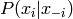 , et l’on
peut montrer facilement que
, et l’on
peut montrer facilement que
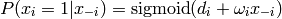
où 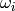 est la i-ème rangée de
est la i-ème rangée de 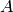 sauf
le i-ème élément, et dans ce modèle la diagonale de
sauf
le i-ème élément, et dans ce modèle la diagonale de 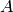 est 0. On voit le lien avec les réseaux de neurones.
est 0. On voit le lien avec les réseaux de neurones.
La Machine de Boltzmann Restreinte¶
En anglais Restricted Boltzmann Machine ou RBM, c’est une
machine de Boltzmann sans connections latérales entre
les 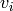 ou entre les
ou entre les 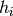 . La fonction
d’énergie devient donc
. La fonction
d’énergie devient donc
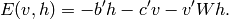
où la matrice A est donc pleine de zéro sauf dans sa sous-matrice W.
L’avantage de cette restriction dans la connectivité est
que l’inférence 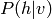 (et aussi
(et aussi 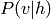 )
devient très facile et analytique et se factorise:
)
devient très facile et analytique et se factorise:
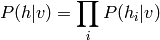
et
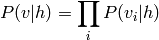
Dans le cas où les variables (= unités) sont binaires, on obtient encore la formule de neurone sigmoidal:
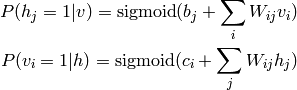
Un autre avantage de la RBM c’est qu’on peut calculer
analytiquement 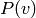 a une constante près
(cette constante est la fonction de partition
a une constante près
(cette constante est la fonction de partition 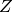 ). Cela permet
aussi de définir une généralisation de la notion de
fonction d’énergie au cas où on veut marginaliser
sur les variables cachées: l’énergie libre
(free energy, aussi inspirée de considérations physiques):
). Cela permet
aussi de définir une généralisation de la notion de
fonction d’énergie au cas où on veut marginaliser
sur les variables cachées: l’énergie libre
(free energy, aussi inspirée de considérations physiques):
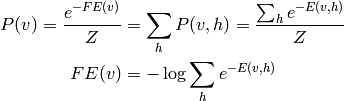
et dans le cas des RBMs, on a
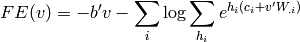
où la somme sur 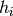 est une somme sur les valeurs que les variables
cachées peuvent prendre, ce qui, dans le cas d’unités binaires donne
est une somme sur les valeurs que les variables
cachées peuvent prendre, ce qui, dans le cas d’unités binaires donne
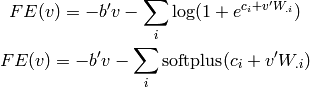
Gibbs dans les RBMs¶
Bien que tirer de 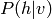 est facile et immédiat dans une RBM,
tirer de
est facile et immédiat dans une RBM,
tirer de 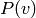 ou de
ou de 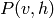 ne peut pas se faire de
manière exacte et se fait donc généralement par une MCMC, la plus commune
étant la MCMC de Gibbs par bloc, où l’on prend avantage du fait
que les tirages
ne peut pas se faire de
manière exacte et se fait donc généralement par une MCMC, la plus commune
étant la MCMC de Gibbs par bloc, où l’on prend avantage du fait
que les tirages 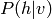 et
et 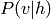 sont faciles:
sont faciles:
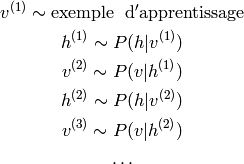
Pour visualiser les données générées à l’étape 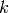 , il vaut mieux utiliser les espérances
(i.e.
, il vaut mieux utiliser les espérances
(i.e. ![E[v^{(k)}_i|h^{(k-1)}]=P(v^{(k)}_i=1|h^{(k-1)})](_images/math/0b24c887f18bba73dd78997bd6147e82133bf11d.png) )
qui sont moins bruitées que les échantillons
)
qui sont moins bruitées que les échantillons 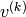 eux-mêmes.
eux-mêmes.
Entraînement des RBMs¶
Le gradient exact sur les paramètres d’une RBM (pour un exemple  ) est
) est
![\frac{\partial \log P(v)}{\partial W} = v' E[h | v] - E[v' h]
\frac{\partial \log P(v)}{\partial b} = E[h | v] - E[h]
\frac{\partial \log P(v)}{\partial c} = v - E[v]](_images/math/9a8b762b1757265330bbcbd4863f3fe25c2680d5.png)
où les espérances sont prises sur la loi de la RBM. Les espérances
conditionnelles sont calculables analytiquement (puisque
![E[h_i | v]=P(h_i=1|v)=](_images/math/b761f88916c58b56ce8cc558c7872804f8534f4b.png) sortie du neurone caché, pour des
sortie du neurone caché, pour des 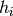 binaires)
mais les espérances inconditionnelles doivent se faire par MCMC.
binaires)
mais les espérances inconditionnelles doivent se faire par MCMC.
Divergence Contrastive¶
La première et plus simple approximation de ![E[v' h]](_images/math/d13085f3fcc28c68acc7c2e0d58afb6f41b35f87.png) , i.e., pour
obtenir des ‘exemples négatifs’ (pour la ‘partie négative’ du gradient),
consiste à faire une courte chaîne de Gibbs (de k étapes) commencée sur un
exemple d’apprentissage. On appelle cet algorithme CD-k
(Contrastive Divergence with k steps). Voir l’algorithme 1
dans Learning Deep Architectures for AI:
, i.e., pour
obtenir des ‘exemples négatifs’ (pour la ‘partie négative’ du gradient),
consiste à faire une courte chaîne de Gibbs (de k étapes) commencée sur un
exemple d’apprentissage. On appelle cet algorithme CD-k
(Contrastive Divergence with k steps). Voir l’algorithme 1
dans Learning Deep Architectures for AI:
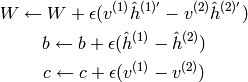
où  est le pas de gradient, et l’on réfère à la notation
de la chaîne de Gibbs des RBMs ci-haut, avec
est le pas de gradient, et l’on réfère à la notation
de la chaîne de Gibbs des RBMs ci-haut, avec
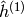 dénote le vecteur des probabilités
dénote le vecteur des probabilités 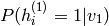 et de la même manière :math:`hat{h}^{(2)}_i=P(h^{(2)}_i=1|v^{(2)}).
et de la même manière :math:`hat{h}^{(2)}_i=P(h^{(2)}_i=1|v^{(2)}).
Ce qui est étonnant c’est que même avec k=1, on obtient des RBMs qui fonctionnent bien dans le sens qu’elles extraient des bonnes caractéristiques des entrées (ce qu’on peut vérifier visuellement en regardant les filtres, les reconstructions stochastiques après 1 étape de Gibbs, ou bien quantitativement en initialisant chaque couche d’un réseau profond avec W et b par pré-entraînement de la RBM associée à chaque couche).
On peut montrer que CD-1 est très proche de l’entraînement d’un auto-encodeur par minimisation de l’erreur de reconstruction, et on voit que l’erreur de reconstruction diminue de manière assez monotone pendant l’entraînement par CD-1.
On peut aussi montrer que CD-k tends vers le vrai gradient (en espérance) quand k devient grand, mais à ce moment on multiplie le temps de calcul par k.
Divergence Contrastive Persistente¶
Pour obtenir un estimateur moins biaisé du vrai gradient sans augmenter
beaucoup le temps de calcul, on peut utiliser l’algorithme de Divergence
Contrastive Persistente (en anglais Persistent Contrastive Divergence,
ou PCD). Plutôt que de redémarrer une chaîne de Gibbs après avoir vu
chaque exemple  , il s’agit de garder une chaîne de Gibbs toujours en activité
pour obtenir nos échantillons d’exemples négatifs. Cette chaîne est
un peu particulière car ses probabilités de transition changent
(lentement), au fur et à mesure qu’on met à jour les paramètres de
la RBM. Soit
, il s’agit de garder une chaîne de Gibbs toujours en activité
pour obtenir nos échantillons d’exemples négatifs. Cette chaîne est
un peu particulière car ses probabilités de transition changent
(lentement), au fur et à mesure qu’on met à jour les paramètres de
la RBM. Soit 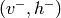 l’état de notre chaîne négative.
L’algorithme d’apprentissage est le suivant:
l’état de notre chaîne négative.
L’algorithme d’apprentissage est le suivant:
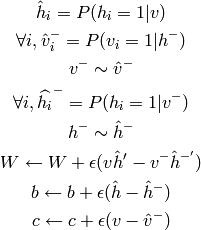
On trouve expérimentalement que PCD est meilleur en terme de génération
d’exemples (et en terme de vraisemblance 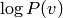 )
que CD-k, et est moins sensible à l’initialisation de la
chaîne de Gibbs.
)
que CD-k, et est moins sensible à l’initialisation de la
chaîne de Gibbs.
RBMs empilés et DBNs¶
On peut utiliser les RBMs comme les auto-encodeurs, pour pré-entraîner de manière
non-supervisée un réseau de neurones profonds, pour ensuite finaliser son entraînement
de manière supervisée habituelle. On va donc empiler les RBMs, la couche cachée
de l’un (étant donnée son entrée), i.e., les 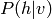 ou bien des
ou bien des
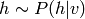 , devenant l’entrée de la couche suivante.
, devenant l’entrée de la couche suivante.
Le pseudo-code de l’entraînement vorace couche par couche d’une pile de RBMs
est présenté dans la section 6.1 (algorithme 2) de
Learning Deep Architectures for AI.
Pour entraîner la k-ième RBM, on propage soit des échantillons
(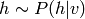 ) ou des posterieurs (
) ou des posterieurs (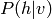 ) à travers
les k-1 premières RBMs, et on les utilise comme données d’entraînement
pour la k-ième RBM. On les entraîne donc une à la fois: une fois qu’on
arrête l’entraînement de la k-ième, on peut procéder à la k+1 ième.
) à travers
les k-1 premières RBMs, et on les utilise comme données d’entraînement
pour la k-ième RBM. On les entraîne donc une à la fois: une fois qu’on
arrête l’entraînement de la k-ième, on peut procéder à la k+1 ième.
Une RBM a la même paramétrisation qu’une couche classique de réseau de neurones
(avec des unités sigmoides), à la différence près qu’on utilise seulement les poids W
et les biais b des unités cachées (car on a seulement besoin de 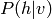 et non pas
de
et non pas
de 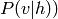 .
.
Deep Belief Networks¶
On peut aussi considérer un empilement de RBMs de manière générative, et l’on appelle ce modèle le Deep Belief Network:
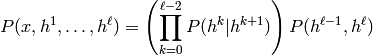
où l’on dénote 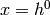 et la variable (vecteur) aléatoire associée à la
couche k est
et la variable (vecteur) aléatoire associée à la
couche k est 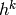 . Les deux dernières couches ont une distribution jointe
qui est donnée par une RBM (la dernière de la pile). Les RBMs du dessous servent
seulement à définir les probabilités conditionnelles
. Les deux dernières couches ont une distribution jointe
qui est donnée par une RBM (la dernière de la pile). Les RBMs du dessous servent
seulement à définir les probabilités conditionnelles 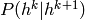 du DBN, où
du DBN, où 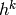 joue le rôle d’unités visibles et
joue le rôle d’unités visibles et 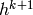 joue
celui des unités cachées dans la RBM k+1.
joue
celui des unités cachées dans la RBM k+1.
Échantilloner d’un DBN se fait donc ainsi:
échantillonner un
de la RBM du dessus (numéro
), par exemple en faisant du Gibbs
- pour k de
à 1
- échantillonner les unités visibles (
) étant données les unités cachées (
) dans la RBM k
retourner le dernier échantillon produit
, qui est le résultat de la génération par le DBN
Dépliement d’une RBM et équivalence RBM - DBN¶
On peut montrer (voir section 8.1 de Learning Deep Architectures for AI.) qu’une RBM correspond à un DBN avec une architecture particulière, dont les poids sont partagés entre toutes les couches: le niveau 1 du DBN utilise les poids W de la RBM, le niveau 2 utilise les poids W’, le niveau 3 utilise les poids W, etc. en alternant entre W et W’. La dernière paire de couches du DBN est une RBM avec les poids W ou W’ selon qu’on déplie un nombre impair ou pair de couches. Remarquons que dans cette équivalence, le DBN a des tailles de couches qui alternent (nombre de visibles de la RBM, nombre de cachées de la RBM, nombre de visibles de la RBM, etc.).
En fait on peut continuer le dépliement d’une RBM jusqu’à l’infini et obtenir un réseau dirigé infini à poids partagés, équivalent. Voir la figure 13 de la même section 8.1. On peut voir que ce réseau infini correspond exactement à une chaîne de Gibbs (infinie) qui culmine (finit) sur la couche visible de la RBM originale, i.e., qui génère les mêmes exemples. Les couches paires correspondent à échantillonner P(v|h) (de la RBM originale) et les couches impaires à échantillonner P(h|v).
Finalement, on peut montrer que si on prend une RBM, qu’on la déplie une fois (en miroir), le fait de continuer l’entraînement de la nouvelle RBM du dessus (initialisée avec W’) va maximiser une borne inférieure sur la vraisemblance du DBN correspondant. Dans le passage d’une RBM à un DBN, on remplace la marginale P(h) de la RBM (qui est obtenue implicitement à travers les paramètres de la RBM, et par exemple une chaîne de Gibbs dans la RBM) par la distribution générée par la partie de DBN au-dessus de cette RBM (le DBN formé de toutes les couches au-dessus de h), puisque ce h correspond aux unités visibles de ce DBN. La démo est simple et instructive, et utilise la lettre Q pour les probabilités selon la RBM (du bas) et la lettre P pour les probabilités selon la DBN obtenue en modélisant les h différemment (i.e. en remplaçant Q(h) par P(h)). On remarque aussi que P(x|h)=Q(x|h), mais ce n’est pas vrai pour P(h|x) et Q(h|x).
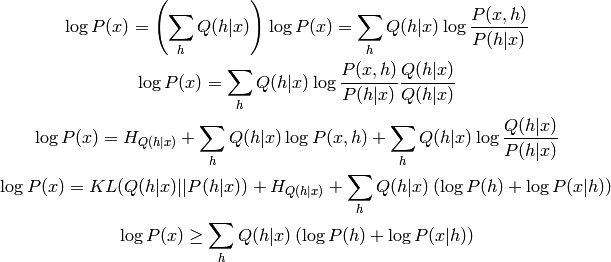
On voit donc effectivement que l’on peut augmenter la borne inférieure (dernière ligne) en faisant de l’entraînement maximum de vraisemblance de P(h) utilisant comme données d’entraînement des h tirés de Q(h|x), où x est tiré de la distribution d’entraînement de la RBM du dessous. Étant donné qu’on a découplé les poids du dessous de ceux du dessus, on ne touche pas à la RBM du dessous (P(x|h) et Q(h|x)), on modifie seulement P(h).
Inférence approximative dans les DBNs¶
Contrairement à la RBM, l’inférence dans les DBNs (choisir les unités cachées
étant données les entrées visibles) est très difficile. Étant donné qu’on
initialise les DBNs comme une pile de RBMs, on utilise en pratique
l’approximation suivante: on échantillonne les 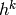 étant
donné les
étant
donné les 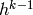 en utilisant les poids du niveau k.
Il s’agirait de l’inférence exacte si c’était effectivement une
RBM isolée, mais ça ne l’est plus avec le DBN.
en utilisant les poids du niveau k.
Il s’agirait de l’inférence exacte si c’était effectivement une
RBM isolée, mais ça ne l’est plus avec le DBN.
On a vu que c’est une approximation à la section précédente parce que la marginale P(h) (du DBN) diffère de la marginale Q(h) (de la RBM du dessous), après qu’on modifie les poids du dessus qui ne sont plus la transposée des poids du dessous, et donc P(h|x) diffère de Q(h|x).
Deep Boltzmann Machine¶
Finalement, on peut aussi utiliser un empilement de RBMs pour initializer une machine de Boltzmann profonde (Salakhutdinov et Hinton, AISTATS 2009). Il s’agit d’une machine de Boltzmann organisée en couches, où chaque couche est seulement connectée à celle du dessous et celle du dessus.
On remarque que les poids sont en quelque sorte deux fois trop gros quand on fait cette initialisation, car maintenant chaque unité reçoit son entrée de la couche au-dessus d’elle et aussi de la couche d’en dessous, alors que dans la RBM originale c’était soit de l’un, ou de l’autre. Salakhutdinov propose donc de diviser les poids par deux quand on fait le passage de l’empilement de RBMs vers la machine de Boltzmann profonde.
Il est intéressant de noter aussi que selon Salakhutdinov, il est crucial de faire l’initialisation de la machine de Boltzmann profonde à partir de l’empilement de RBMs, plutôt qu’à partir de poids aléatoires. Cela suggère que la difficulté d’entraînement des réseaux MLP profonds déterministes ne leur est pas unique, et qu’une difficulté semblable se retrouve dans les machines de Boltzmann profondes. Dans les deux cas, le fait d’initialiser chaque couche selon un entraînement local à la couche semble aider beaucoup. Salakutdinov obtient des résultats meilleurs avec sa machine de Boltzmann profonde qu’avec un DBN équivalent, mais l’entraînement est plus long.