Classifying MNIST digits using Logistic Regression¶
Note
This sections assumes the reader is familiar with the following Theano concepts: shared variables , basic arithmetic ops , T.grad .
TODO: shared variables documentation not up !!
TODO: put shortcuts to the downloads right here (the download for the full source)
In this section, we show how Theano can be used to implement the most basic classifier: the logistic regression. We start off with a quick primer of the model, which serves both as a refresher but also to anchor the notation and show how mathematical expressions are mapped onto Theano graphs.
In the deepest of machine learning traditions, this tutorial will tackle the exciting problem of MNIST digit classification.
The Model¶
Logistic regression is a probabilistic, linear classifier. It is parametrized
by a weight matrix 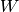 and a bias vector
and a bias vector 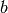 . Classification is
done by projecting data points onto a set of hyperplanes, the distance to
which reflects a class membership probability.
. Classification is
done by projecting data points onto a set of hyperplanes, the distance to
which reflects a class membership probability.
Mathematically, this can be written as:

The output of the model or prediction is then done by taking the argmax of the vector whose i’th element is P(Y=i|x).
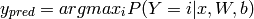
The code to do this in Theano is the following:
# generate symbolic variables for input (x and y represent a
# minibatch)
x = T.fmatrix()
y = T.lvector()
# allocate shared variables model params
b = theano.shared(numpy.zeros((10,)))
W = theano.shared(numpy.zeros((784,10)))
# symbolic expression for computing the vector of
# class-membership probabilities
p_y_given_x = T.softmax(T.dot(x,w)+b)
# compiled Theano function that returns the vector of class-membership
# probabilities
get_p_y_given_x = theano.function( x, p_y_given_x)
# print the probability of some example represented by x_value
# x_value is not a symbolic variable but a numpy array describing the
# datapoint
print 'Probability that x is of class %i is %f' % i, get_p_y_given_x(x_value)[i]
# symbolic description of how to compute prediction as class whose probability
# is maximal
y_pred = T.argmax(p_y_given_x)
# compiled theano function that returns this value
classify = theano.function(x, y_pred)
We first start by allocating symbolic variables for the inputs  .
Since the parameters of the model must maintain a persistent state throughout
training, we allocate shared variables for
.
Since the parameters of the model must maintain a persistent state throughout
training, we allocate shared variables for 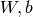 .
This declares them both as being symbolic Theano variables, but also
initializes their contents. The dot and softmax operators are then used to compute the vector
.
This declares them both as being symbolic Theano variables, but also
initializes their contents. The dot and softmax operators are then used to compute the vector
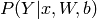 . The resulting variable p_y_given_x is a symbolic variable
of vector-type.
. The resulting variable p_y_given_x is a symbolic variable
of vector-type.
Up to this point, we have only defined the graph of computations which Theano
should perform. To get the actual numerical value of 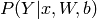 , we
must create a function get_p_y_given_x, which takes as input x and
returns p_y_given_x. We can then index its return value with the
index
, we
must create a function get_p_y_given_x, which takes as input x and
returns p_y_given_x. We can then index its return value with the
index 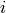 to get the membership probability of the
to get the membership probability of the 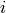 th class.
th class.
Now let’s finish building the Theano graph. To get the actual model prediction, we can use the T.argmax operator, which will return the index at which p_y_given_x is maximal (i.e. the class with maximum probability).
Again, to calculate the actual prediction for a given input, we construct a function classify. This function takes as argument a batch of inputs x (as a matrix), and outputs a vector containing the predicted class for each example (row) in x.
Now of course, the model we have defined so far does not do anything useful yet, since its parameters are still in their initial random state. The following section will thus cover how to learn the optimal parameters.
Note
For a complete list of Theano ops, see: list of ops
Defining a Loss Function¶
Learning optimal model parameters involves minimizing a loss function. In the
case of multi-class logistic regression, it is very common to use the negative
log-likelihood as the loss. This is equivalent to maximizing the likelihood of the
data set 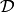 under the model parameterized by
under the model parameterized by 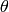 . Let
us first start by defining the likelihood
. Let
us first start by defining the likelihood 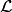 and loss
and loss
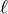 :
:
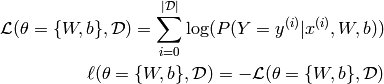
While entire books are dedicated to the topic of minimization, gradient descent is by far the simplest method for minimizing arbitrary non-linear functions. This tutorial will use the method of stochastic gradient method with mini-batches (MSGD). See Stochastic Gradient Descent for more details.
The following Theano code defines the (symbolic) loss for a given minibatch:
loss = -T.sum(T.log(p_y_given_x)[T.arange(y.shape[0]), y])
# note on syntax: T.arange(y,shape[0]) is a vector of integers [0,1,2,...,len(y)].
# Indexing a matrix M by the two vectors [0,1,...,K], [a,b,...,k] returns the
# elements M[0,a], M[1,b], ..., M[K,k] as a vector. Here, we use this
# syntax to retrieve the log-probability of the correct labels, y.
Note
In practice, we will use the mean (T.mean) instead of the sum. This allows for the learning rate choice to be less dependent of the minibatch size.
Creating a LogisticRegression class¶
We now have all the tools we need to define a LogisticRegression class, which encapsulates the basic behaviour of logistic regression. The code is very similar to what we have covered so far, and should be self explanatory.
class LogisticRegression(object):
def __init__(self, input, n_in, n_out):
""" Initialize the parameters of the logistic regression
:param input: symbolic variable that describes the input of the
architecture (e.g., one minibatch of input images)
:param n_in: number of input units, the dimension of the space in
which the datapoint lies
:param n_out: number of output units, the dimension of the space in
which the target lies
"""
# initialize with 0 the weights W as a matrix of shape (n_in, n_out)
self.W = theano.shared( value=numpy.zeros((n_in,n_out),
dtype = theano.config.floatX) )
# initialize the baises b as a vector of n_out 0s
self.b = theano.shared( value=numpy.zeros((n_out,),
dtype = theano.config.floatX) )
# compute vector of class-membership probabilities in symbolic form
self.p_y_given_x = T.nnet.softmax(T.dot(input, self.W)+self.b)
# compute prediction as class whose probability is maximal in
# symbolic form
self.y_pred=T.argmax(self.p_y_given_x, axis=1)
def negative_log_likelihood(self, y):
"""Return the negative log-likelihood of the prediction of this
model under a given target distribution.
.. math::
\mathcal{L} (\theta=\{W,b\}, \mathcal{D}) =
\sum_{i=0}^{|\mathcal{D}|} \log(P(Y=y^{(i)}|x^{(i)}, W,b)) \\
\ell (\theta=\{W,b\}, \mathcal{D})
:param y: corresponds to a vector that gives for each example the
correct label;
note: in practice we use mean instead of sum so that
learning rate is less dependent on the batch size
"""
return -T.mean(T.log(self.p_y_given_x)[T.arange(y.shape[0]),y])
We instantiate this class as follows:
# allocate symbolic variables for the data
x = T.fmatrix() # the data is presented as rasterized images (each being a 1-D row vector in x)
y = T.lvector() # the labels are presented as 1D vector of [long int] labels
# construct the logistic regression class
classifier = LogisticRegression( \
input=x.reshape((batch_size,28*28)), n_in=28*28, n_out=10)
Note that the inputs x and y are defined outside the scope of the LogisticRegression object. Since the class requires the input x to build its graph however, it is passed as a parameter of the __init__ function.
The last step involves defining a (symbolic) cost variable to minimize, using the instance method classifier.negative_log_likelihood.
cost = classifier.negative_log_likelihood(y)
Note that the return value of classifier.negative_log_likelihood is a vector containing the cost for each training example within the minibatch. Since we are using MSGD, the cost to minimize is the mean cost across the minibatch. Note how x is an implicit symbolic input to the symbolic definition of cost, here, because classifier.__init__ has defined its symbolic variables in terms of x.
Learning the Model¶
To implement MSGD in most programming languages (C/C++, Matlab, Python), one
would start by manually deriving the expressions for the gradient of the loss
with respect to the parameters: in this case 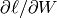 ,
and
,
and 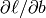 , This can get pretty tricky for complex
models, as expressions for
, This can get pretty tricky for complex
models, as expressions for 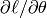 can get
fairly complex, especially when taking into account problems of numerical
stability.
can get
fairly complex, especially when taking into account problems of numerical
stability.
With Theano, this work is greatly simplified as it performs automatic differentiation and applies certain math transforms to improve numerical stability.
To get the gradients 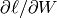 and
and
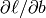 in Theano, simply do the following:
in Theano, simply do the following:
# compute the gradient of cost with respect to theta = (W,b)
g_W = T.grad(cost, classifier.W)
g_b = T.grad(cost, classifier.b)
g_W and g_b are again symbolic variables, which can be used as part of a computation graph. Performing one-step of gradient descent can then be done as follows:
# set a learning rate
learning_rate=0.01
# specify how to update the parameters of the model as a dictionary
updates ={classifier.W: classifier.W - numpy.asarray(learning_rate)*g_W,\
classifier.b: classifier.b - numpy.asarray(learning_rate)*g_b}
# compiling a Theano function `train_model` that returns the cost, but in
# the same time updates the parameter of the model based on the rules
# defined in `updates`
train_model = theano.function([x, y], cost, updates = updates )
The updates dictionary contains, for each parameter, the stochastic gradient update operation. The function train_model is then defined such that:
- the inputs are the mini-batch
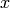 with corresponding labels
with corresponding labels 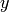
- the return value is the cost/loss associated with inputs x, y
- on every function call, it will apply the operations defined by the updates dictionary.
Each time train_model(x,y) function is called, it will thus compute and return the appropriate cost, while also performing a step of MSGD. The entire learning algorithm thus consists in looping over all examples in the dataset, and repeatedly calling the train_model function.
Testing the model¶
As explained in Learning a Classifier, when testing the model we are interested in the number of misclassified examples (and not only in the likelihood). The LogisticRegression class therefore has an extra instance method, which builds the symbolic graph for retrieving the number of misclassified examples in each minibatch.
The code is as follows:
class LogisticRegression(object):
...
def errors(self, y):
"""Return a float representing the number of errors in the minibatch
over the total number of examples of the minibatch ; zero
one loss over the size of the minibatch
"""
return T.mean(T.neq(self.y_pred, y))
We then create a function test_model, which we can call to retrieve this value. As you will see shortly, test_model is key to our early-stopping implementation (see Early-Stopping).
test_model = theano.function([x,y], classifier.errors(y))
Putting it All Together¶
The finished product is as follows.
The user can learn to classify MNIST digits with SGD logistic regression, by typing, from within the DeepLearningTutorials folder:
python code/logistic_sgd.py
The output one should expect is of the form :
epoch 0, minibatch 2500/2500, validation error 10.720000 %
epoch 0, minibatch 2500/2500, test error of best model 11.050000 %
...
epoch 96, minibatch 2500/2500, validation error 7.010000 %
Optimization complete with best validation score of 7.01%, with test performance 7.61%
The code ran for 2.979333 minutes
On an Intel(R) Core(TM)2 Duo CPU E8400 @ 3.00 Ghz the code runs with approximately 1.862083125 sec/epoch and it took 96 epochs to reach a test error of 7.61%.
Footnotes
| [1] | For smaller datasets and simpler models, more sophisticated descent algorithms can be more effective. The sample code logistic_cg.py demonstrates how to use SciPy’s conjugate gradient solver with Theano on the logistic regression task. |