Probabilistic models for deep architectures¶
Of particular interest are Boltzmann machine models, certain variants of which are used in deep architectures such as Deep Belief Networks and Deep Boltzmann Machines. See section 5 of Learning Deep Architectures for AI.
The Boltzmann distribution is generally defined on binary variables
 , with
, with
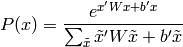
where the denominator is simply a normalizing constant such that
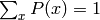 , and the
, and the  indicates the nature
of the interaction (e.g. a positive value indicates that
indicates the nature
of the interaction (e.g. a positive value indicates that 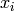 et
et 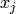 prefer to take the same value) between pairs of
variables, and
prefer to take the same value) between pairs of
variables, and 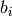 indicates the inclination of a given
indicates the inclination of a given
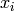 to take a value of 1.
to take a value of 1.
Readings on probabilistic graphical models¶
See
Graphical models: probabilistic inference. M. I. Jordan and Y. Weiss. In M. Arbib (Ed.), The Handbook of Brain Theory and Neural Networks, 2nd edition. Cambridge, MA: MIT Press, 2002.
Certain distributions can be written 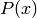 for
a vector of variables
for
a vector of variables 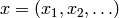 in the form
in the form
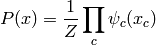
where 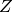 is the normalizing constant (called the partition function),
and the product is over cliques (subsets
is the normalizing constant (called the partition function),
and the product is over cliques (subsets 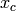 of elements of the vector
of elements of the vector 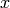 ),
and the
),
and the  are functions (one per clique) that indicate how
the variables in each clique interact.
are functions (one per clique) that indicate how
the variables in each clique interact.
A particular case where 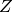 may be simplified a bit (factorized
over cliques) is the case of directed models where variables
are structured as a directed acyclic graph, with a topological ordering
that associates a group of parent variables
may be simplified a bit (factorized
over cliques) is the case of directed models where variables
are structured as a directed acyclic graph, with a topological ordering
that associates a group of parent variables  with
each variable
with
each variable 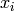 :
:
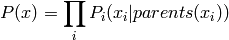
where it can be seen that there is one clique for a variable and its parents,
i.e.,  .
.
In the general case (represented with an undirected graph), the
potential functions 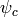 are directly parameterized,
often in the space of logarithms of
are directly parameterized,
often in the space of logarithms of 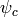 ,
leading to a formulation known as a Markov random field:
,
leading to a formulation known as a Markov random field:
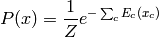
where:math:E(x)=sum_c E_c(x_c) is called the energy function.
The energy function of a Boltzmann machine is a second degree polynomial
in 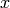 . The most common parameterization of Markov random fields
has the following form, which is log-linear:
. The most common parameterization of Markov random fields
has the following form, which is log-linear:
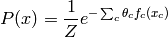
where the only free parameters are the  ,
and where the complete log likelihood (when
,
and where the complete log likelihood (when 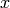 is completely observed in each training example) is log-linear
in the parameters
is completely observed in each training example) is log-linear
in the parameters  . One can easily
show that this function is convex in
. One can easily
show that this function is convex in  .
.
Inference¶
One of the most important obstacles in the practical application of
the majority of probabilistic models is the difficulty of inference:
given certain variables (a subset of 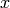 ),
predict the marginal distribution (separately for each) or joint
distribution of certain other variables.
Let
),
predict the marginal distribution (separately for each) or joint
distribution of certain other variables.
Let  with
with 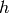 (hidden) being the variables
we would like to predict, and
(hidden) being the variables
we would like to predict, and  (visible)
being the observed subset.
One would like to calculate, or at least sample from,
(visible)
being the observed subset.
One would like to calculate, or at least sample from,
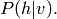
Inference is obviously useful if certain variables are missing, or if, while using the model, we wish to predict a certain variable (for example the class of an image) given some other variables (for example, the image itself). Note that if the model has hidden variables (variables that are never observed in the data) we do not try to predict the values directly, but we will still implicitly marginalize over these variables (sum over all configurations of these variables).
Inference is also an essential component of learning, in order to calculate gradients (as seen below in the case of Boltzmann machines) or in the use of the Expectation-Maximization (EM) algorithm which requires a marginalization over all hidden variables.
In general, exact inference has a computational cost exponential in the size of the cliques of a graph (in fact, the unobserved part of the graph) because we must consider all possible combinations of values of the variables in each clique. See section 3.4 of Graphical models: probabilistic inference for a survey of exact inference methods.
A simplifed form of inference consists of calculating not the entire distribution, but only the mode (the most likely configuration of values) of the distribution:
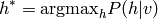
This is known as MAP = Maximum A Posteriori inference.
Approximate inference¶
The two principal families of methods for approximate inference in probabilistic models are Markov chain Monte Carlo (MCMC) methods and variational inference.
The principle behind variational inference is the following. We will define a simpler model than the target model (the one that interests us), in which inference is easy, with a similar set of variables (though generally with more simple dependencies between variables than those contained in the target model). We then optimize the parameters of the simpler model so as to approximate the target model as closely as possible. Finally, we do inference using the simpler model. See section 4.2 of Graphical models: probabilistic inference for more details and a survey.
Inference with MCMC¶
In general 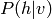 can be exponentially expensive to represent (in
terms of the number of hidden variables, because we must consider all possible
configurations of
can be exponentially expensive to represent (in
terms of the number of hidden variables, because we must consider all possible
configurations of 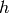 ). The principle behind Monte Carlo inference is
that we can approximate the distribution
). The principle behind Monte Carlo inference is
that we can approximate the distribution 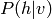 using samples from
this distribution. Indeed, in practice we only need an expectation (for
example, the expectation of the gradient) under this conditional distribution.
We can thus approximate the desired expectation with an average of these
samples.
using samples from
this distribution. Indeed, in practice we only need an expectation (for
example, the expectation of the gradient) under this conditional distribution.
We can thus approximate the desired expectation with an average of these
samples.
See the page site du zéro sur Monte-Carlo (in French) for a gentle introduction.
Unfortunately, for most probabilistic models, even sampling from 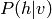 exactly is not feasible (taking time exponential in the dimension of de
exactly is not feasible (taking time exponential in the dimension of de
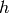 ). Therefore the most general approach is based on an approximation
of Monte-Carlo sampling called Markov chain Monte Carlo (MCMC).
). Therefore the most general approach is based on an approximation
of Monte-Carlo sampling called Markov chain Monte Carlo (MCMC).
A (first order) Markov chain is a sequence of random variables
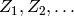 , where
, where  is independent of
is independent of
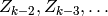 given
given  :
:
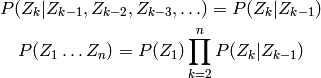
The goal of MCMC is to construct a Markov chain whose asymptotic
marginal distribution, i.e. the distribution of 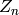 as
as
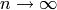 , converges towards a given target
distribution, such as
, converges towards a given target
distribution, such as 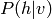 or
or 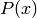 .
.
Gibbs sampling¶
Numerous MCMC-based sampling methods exist. The one most commonly used for deep architectures is Gibbs sampling. It is simple and has a certain plausible analogy with the functioning of the brain, where each neuron decides to send signals with a certain probability as a function of the signals it receives from other neurons.
Let us suppose that we wish to sample from the distribution 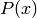 where
where 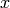 is a set of variables
is a set of variables 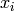 (we could optionally
have a set of variables upon which we have conditioned, but this would
not change the procedure, so we ignore them in the following description).
(we could optionally
have a set of variables upon which we have conditioned, but this would
not change the procedure, so we ignore them in the following description).
Let 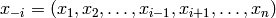 , i.e.
all variables in
, i.e.
all variables in 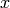 excluding
excluding 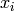 . Gibbs sampling is
performed using the following algorithm:
. Gibbs sampling is
performed using the following algorithm:
- Choose an initial value of
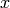 in an arbitrary manner (random or not)
in an arbitrary manner (random or not) - For each step of the Markov chain:
- Iterate over each
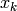 in
in 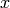
- Draw
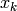 from the conditional distribution
from the conditional distribution 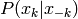
- Draw
- Iterate over each
In some cases one can group variables in 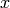 into blocks or groups of
variables such that drawing samples for an entire group, given the others, is
easy. In this case it is advantageous to interpret the algorithm above with
into blocks or groups of
variables such that drawing samples for an entire group, given the others, is
easy. In this case it is advantageous to interpret the algorithm above with
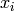 as the
as the 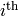 group rather than the
group rather than the
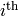 variable. This is known as block Gibbs sampling.
variable. This is known as block Gibbs sampling.
The gradient in a log-linear Markov random field¶
See Learning Deep Architectures for AI for detailed derivations.
Log-linear Markov random fields are undirected probabilistic models where
the energy function is linear in the parameters  of the model:
of the model:
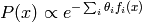
where 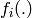 are known as sufficient statistics
of the model, because the expectations
are known as sufficient statistics
of the model, because the expectations ![E[f_i(x)]](_images/math/3eba7a57afb4739b629719623a47a16ec9472f85.png) are
sufficient for characterizing the distribution and estimating parameters.
are
sufficient for characterizing the distribution and estimating parameters.
Note that 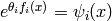 is associated with
each clique in the model (in general, only a sub-vector of
is associated with
each clique in the model (in general, only a sub-vector of 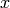 influences each
influences each 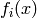 ).
).
Getting back to sufficient statistics, one can show that the gradient of the log likelihood is as follows:
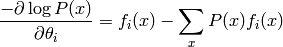
and the average gradient over training examples 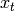 is thus
is thus
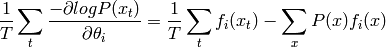
Thus, it is clear that the gradient vanishes when the average of the sufficient statistics under the training distribution equals their expectation under the model distribution :math:`P`.
Unfortunately, calculating this gradient is difficult. We do not want
to sum over all possible 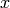 , but fortunately one can obtain
a Monte-Carlo approximation by one or more samples from
, but fortunately one can obtain
a Monte-Carlo approximation by one or more samples from 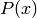 ,
which gives us a noisy estimate of the gradient. In general, however,
even to obtain an unbiased sample from
,
which gives us a noisy estimate of the gradient. In general, however,
even to obtain an unbiased sample from 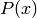 is exponentially
costly, and thus one must use an MCMC method.
is exponentially
costly, and thus one must use an MCMC method.
We refer to the terms of the gradient due to the numerator of
the probability density (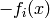 ) as the ‘positive phase’
gradient, and the terms of the gradient corresponding to the partition
function (denominator of the probability density) as the
‘negative phase’ gradient.
) as the ‘positive phase’
gradient, and the terms of the gradient corresponding to the partition
function (denominator of the probability density) as the
‘negative phase’ gradient.
The Boltzmann Machine¶
A Boltzmann machine is an undirected probabilistic model, a particular
form of log-linear Markov random field, containing both visible and hidden
variables, where the energy function is a second degree polynomial of
the variables 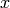 :
:

The classic Boltzmann machine has binary variables and
inference is conducted via Gibbs sampling, which requires samples
from 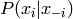 . It can be easily shown that
. It can be easily shown that

where 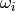 is the
is the 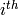 row of
row of 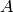 excluding
the
excluding
the 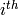 element (the diagonal of
element (the diagonal of 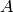 is 0 in this model). Thus, we see the link with networks of neurons.
is 0 in this model). Thus, we see the link with networks of neurons.
Restricted Boltzmann Machines¶
A Restricted Boltzmann Machine, or RBM, is a Boltzmann machine without
lateral connections between the visible units 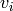 or between
the hidden units
or between
the hidden units 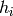 . The energy function thus becomes
. The energy function thus becomes
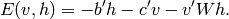
where the matrix 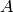 is entirely 0 except in the submatrix
is entirely 0 except in the submatrix 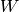 .
The advantage of this connectivity restriction is that inferring
.
The advantage of this connectivity restriction is that inferring
 (and also
(and also 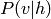 ) becomes very easy, can be performed
analytically, and the distribution factorizes:
) becomes very easy, can be performed
analytically, and the distribution factorizes:

and
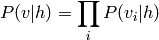
In the case where the variables (“units”) are binary, we obtain once again have a sigmoid activation probability:
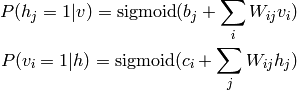
Another advantage of the RBM is that the distribution 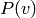 can
be calculated analytically up to a constant (the unknown constant
being the partition function). This permits us to define a generalization
of the notion of an energy function in the case when we wish to marginalize
over the hidden variables: the free energy (inspired by notions from
physics)
can
be calculated analytically up to a constant (the unknown constant
being the partition function). This permits us to define a generalization
of the notion of an energy function in the case when we wish to marginalize
over the hidden variables: the free energy (inspired by notions from
physics)
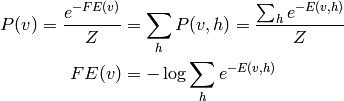
and in the case of RBMs, we have
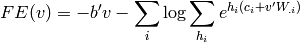
where the sum over 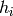 is a sum over values that the hidden variables
can take, which in the case of binary units yields
is a sum over values that the hidden variables
can take, which in the case of binary units yields
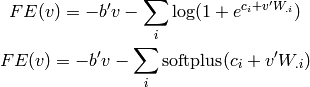
Gibbs sampling in RBMs¶
Although sampling from  is easy and immediate in an RBM,
drawing samples from
is easy and immediate in an RBM,
drawing samples from 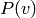 or from
or from 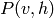 cannot be done
exactly and is thus generally accomplished with MCMC, most commonly with
block Gibbs sampling, where we take advantage of the fact that
sampling from
cannot be done
exactly and is thus generally accomplished with MCMC, most commonly with
block Gibbs sampling, where we take advantage of the fact that
sampling from  and
and 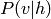 is easy:
is easy:

In order to visualize the generated data at step 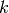 , it is better
to use expectations (i.e.
, it is better
to use expectations (i.e. ![E[v^{(k)}_i|h^{(k-1)}]=P(v^{(k)}_i=1|h^{(k-1)})](_images/math/0b24c887f18bba73dd78997bd6147e82133bf11d.png) )
which are less noisy than the samples
)
which are less noisy than the samples 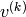 themselves.
themselves.
Training RBMs¶
The exact gradient of the parameters of an RBM (for an example  ) is
) is
![\frac{\partial \log P(v)}{\partial W} = v' E[h | v] - E[v' h]
\frac{\partial \log P(v)}{\partial b} = E[h | v] - E[h]
\frac{\partial \log P(v)}{\partial c} = v - E[v]](_images/math/9a8b762b1757265330bbcbd4863f3fe25c2680d5.png)
where the expectations are under the distribution of the RBM. The conditional
expectations can be calculated analytically (since ![E[h_i | v]=P(h_i=1|v)=](_images/math/b761f88916c58b56ce8cc558c7872804f8534f4b.png) the output of a hidden unit, for binary
the output of a hidden unit, for binary 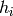 )
but the unconditional expectations must be approximated using MCMC.
)
but the unconditional expectations must be approximated using MCMC.
Contrastive Divergence¶
The first and simplest approximation of ![E[v' h]](_images/math/d13085f3fcc28c68acc7c2e0d58afb6f41b35f87.png) , i.e., for
obtaining ‘negative examples’ (for the ‘negative phase’ gradient),
consists of running a short Gibbs chain (of
, i.e., for
obtaining ‘negative examples’ (for the ‘negative phase’ gradient),
consists of running a short Gibbs chain (of 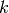 steps) beginning at
a training example. This algorithm is known as CD-k
(Contrastive Divergence with k steps). See algorithm 1
in Learning Deep Architectures for AI:
steps) beginning at
a training example. This algorithm is known as CD-k
(Contrastive Divergence with k steps). See algorithm 1
in Learning Deep Architectures for AI:
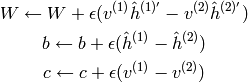
where  is the gradient step size, and we refer to the
notation for Gibbs sampling from RBMs above, with
is the gradient step size, and we refer to the
notation for Gibbs sampling from RBMs above, with
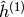 denotes the vector of probabilities
denotes the vector of probabilities  and in the same fashion
and in the same fashion 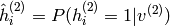 .
.
What is surprising is that even with 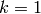 , we obtain
RBMs that work well in the sense that they extract good features
from the data (which we can verify visually byt looking at the filters,
the stochastic reconstructions after one step of Gibbs, or quantitatively
by initializing each layer of a deep network with
, we obtain
RBMs that work well in the sense that they extract good features
from the data (which we can verify visually byt looking at the filters,
the stochastic reconstructions after one step of Gibbs, or quantitatively
by initializing each layer of a deep network with 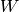 and
and
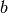 obtained by pretraining an RBM at each layer).
obtained by pretraining an RBM at each layer).
It can be shown that CD-1 is very close to the training procedure of an autoencoder by minimizing reconstruction error, and one can see that the reconstruction error diminishes in a mostly monotonic fashion during CD-1 training.
It can also be shown that CD-k tends to the true gradient (in expected value) when k becomes large, but at the same time increases computation time by a factor of k.
Persistent Contrastive Divergence¶
In order to obtain a less biased estimator of the true gradient without
significantly increasing the necessary computation time, we can use the
Persistent Contrastive Divergence (PCD) algorithm. Rather than restarting
a Gibbs chain after each presentation of a training example  ,
PCD keeps a chain running in order to obtain negative examples. This chain
is a bit peculiar because its transition probabilities change (slowly) as
we update the parameters of the RBM. Let
,
PCD keeps a chain running in order to obtain negative examples. This chain
is a bit peculiar because its transition probabilities change (slowly) as
we update the parameters of the RBM. Let 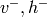 be the state
of our negative phase chain. The learning algorithm is then
be the state
of our negative phase chain. The learning algorithm is then

Experimentally we find that PCD is better in terms of generating examples
that resemble the training data (and in terms of the likelihood
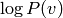 ) than CD-k, and is less sensitive to the initialization
of the Gibbs chain.
) than CD-k, and is less sensitive to the initialization
of the Gibbs chain.
Stacked RBMs and DBNs¶
RBMs can be used, like autoencoders, to pretrain a deep neural network in an
unsupervised manner, and finish training in the usual supervised fashion.
One stacks RBMs with the hidden layer of one (given its input) i.e., les
 or
or 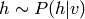 , becomes the data for the next
layer.
, becomes the data for the next
layer.
The pseudocode for greedy layer-by-layer training of a stack of RBMs
is presented in section 6.1 (algorithm 2) of Learning Deep Architectures
for AI. To train the 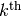 RBM, we propagate forward
samples
RBM, we propagate forward
samples 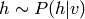 or the posteriors
or the posteriors  through
the
through
the 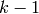 previously trained RBMs and use them as data for training
the
previously trained RBMs and use them as data for training
the 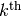 RBM. They are trained one at a time: once
we stop training the
RBM. They are trained one at a time: once
we stop training the 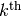 , we move on to the
, we move on to the
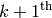 .
.
An RBM has the same parameterization as a layer in a classic neural network
(with logistic sigmoid hidden units), with the difference that we use
only the weights 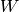 and the biases
and the biases 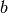 of the hidden units
(since we only need
of the hidden units
(since we only need  and not
and not 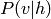 ).
).
Deep Belief Networks¶
We can also consider a stacking of RBMs in a generative manner, and we call these models Deep Belief Networks:
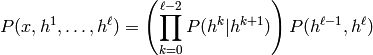
where we denote  and
and  as the random variable (vector)
associated with layer
as the random variable (vector)
associated with layer 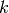 . The last two layers have a joint distribution
given by an RBM (the last of the stack). The RBMs below serve
only to define the conditional probabilities
. The last two layers have a joint distribution
given by an RBM (the last of the stack). The RBMs below serve
only to define the conditional probabilities 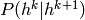 of the DBN, where
of the DBN, where  play the role of visible units and
:math:`h^{k+1}`similarly play the role of hidden units in RBM k+1.
play the role of visible units and
:math:`h^{k+1}`similarly play the role of hidden units in RBM k+1.
Sampling from a DBN is thus performed as follows:
Sample a
from the top RBM (number
), for example by running a Gibbs chain
- For k from
to 1
- sample the visible units (
) given the hidden units (
) in RBM k
Return
, the last sample obtained, which is the result of generating from the DBN
Unfolding an RBM and RBM - DBN equivalence¶
It can be shown (see section 8.1 of
Learning Deep Architectures for AI.)
that an RBM corresponds to DBN with a particular architecture, where the
weights are shared between all the layers:
level 1 of the DBN uses the weights 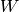 of the RBM,
level 2 uses the weights
of the RBM,
level 2 uses the weights 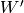 , level 3 uses
, level 3 uses 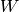 , etc. alternating
between
, etc. alternating
between 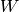 and
and 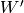 . The last pair of layers of the DBN is an RBM with weights
. The last pair of layers of the DBN is an RBM with weights 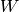 or :math`W’` depending on whether the number of layers
is odd or even.
Note that in this equivalence, the DBN has layer sizes that alternate
(number of visible units of the RBM, number of hidden units of the RBM,
number of visibles, etc.)
or :math`W’` depending on whether the number of layers
is odd or even.
Note that in this equivalence, the DBN has layer sizes that alternate
(number of visible units of the RBM, number of hidden units of the RBM,
number of visibles, etc.)
In fact we can continue the unfolding of an RBM infinitely and obtain an infinite directed network with shared weights, equivalently. See figure 13 in the same section, 8.1.
It can be seen that this infinite network corresponds exactly to an infinite
Gibbs chain that leads to (finishes on) the visible layer of the original
RBM, i.e. that generates the same examples. The even layers correspond to
sampling 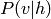 (of the original RBM) and the odd layers to
sampling
(of the original RBM) and the odd layers to
sampling  .
.
Finally, it can be shown that if we take an RBM and unfold it one time
(mirrored), the continued training of the new RBM on top (initialized
with 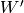 ) maximizes a lower bound on the log likelihood of the
corresponding DBN. In passing from an RBM to a DBN, we replace the marginal
distribution
) maximizes a lower bound on the log likelihood of the
corresponding DBN. In passing from an RBM to a DBN, we replace the marginal
distribution 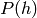 of the RBM (which is encoded implicitly in
the parameters of the RBM) with the distribution generated by the part of
the DBN above this RBM (the DBN consists of all layers above
of the RBM (which is encoded implicitly in
the parameters of the RBM) with the distribution generated by the part of
the DBN above this RBM (the DBN consists of all layers above 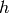 ),
since this
),
since this 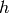 corresponds to visible units of this DBN. The proof
is simple and instructive, and uses the letter Q for the probabilities
according to the RBM (at the bottom) and the letter P for the probabilities
according to the DBN obtained by modeling
corresponds to visible units of this DBN. The proof
is simple and instructive, and uses the letter Q for the probabilities
according to the RBM (at the bottom) and the letter P for the probabilities
according to the DBN obtained by modeling 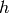 differently (i.e.
by replacing
differently (i.e.
by replacing 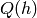 by
by 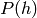 ). We also remark that
). We also remark that
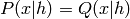 , but this is not true for
, but this is not true for 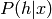 and
and
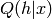 .
.

This shows that one can actually increase the lower bound (last line) by
doing maximum likelihood training of 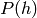 using as training data the
using as training data the
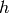 drawn from
drawn from 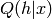 , where
, where 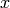 is drawn from the
training distribution of the bottom RBM. Since we have decoupled the weights
below from those above, we don’t touch the bottom RBM (
is drawn from the
training distribution of the bottom RBM. Since we have decoupled the weights
below from those above, we don’t touch the bottom RBM (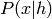 and
and
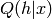 ), and only modify
), and only modify 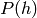 .
.
Approximate inference in DBNs¶
Contrary to the RBM, inference in DBNs (inferring the states of the hidden
units given the visible units) is very difficult. Given that we
initialize DBNs as a stack of RBMs, in practice the following approximation
is used: sample the  given the
given the  using the new
weights of level
using the new
weights of level 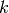 . This would be exact inference if this was
still an isolated RBM, but it is no longer exact with the DBN.
. This would be exact inference if this was
still an isolated RBM, but it is no longer exact with the DBN.
We saw that this is an approximation in the previous section because the
marginal 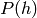 (of the DBN) differs from the marginal
(of the DBN) differs from the marginal 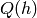 (of the bottom RBM), after modifying the upper weights so that they are
no longer the tranpose of the bottom weights, and thus
(of the bottom RBM), after modifying the upper weights so that they are
no longer the tranpose of the bottom weights, and thus 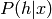 differs from
differs from 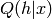 .
.
Deep Boltzmann Machines¶
Finally, we can also use a stack of RBMs for initializing a deep Boltzmann machine (Salakhutdinov and Hinton, AISTATS 2009). This is a Boltzmann machine organized in layers, where each layer is connected the layer below and the layer above, and there are no within-layer connections.
Note that the weights are somehow two times too big when doing the initialization described above, since now each unit receives input from the layer above and the layer below, whereas in the original RBM it was either one or the other. Salakhutdinov proposes thus dividing the weights by two when we make the transition from stacking RBMs to deep Boltzmann machines.
It is also interesting to note that according to Salakhutdinov, it is crucial to initialize deep Boltzmann machines as a stack of RBMs, rather than with random weights. This suggests that the difficulty of training deep deterministic MLP networks is not unique to MLPs, and that a similar difficulty is found in deep Boltzmann machines. In both cases, the initialization of each layer according to a local training procedure seems to help a great deal. Salakhutdinov obtains better results with his deep Boltzmann machine than with an equivalent-sized DBN, although training the deep Boltzmann machine takes longer.
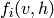 . The average gradient
of the negative log likelihood of the observed data is thus
. The average gradient
of the negative log likelihood of the observed data is thus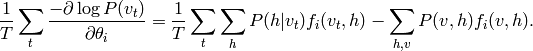
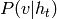 .
.