Introduction à l’apprentissage par descente de gradient¶
Considérons une fonction de coût  , qui associe un vecteur de
paramètres
, qui associe un vecteur de
paramètres  à un scalaire
à un scalaire 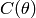 , que nous voulons
minimiser. En apprentissage machine, la fonction de coût est généralement la
moyenne, ou l’espérance, de la fonction d’erreur
, que nous voulons
minimiser. En apprentissage machine, la fonction de coût est généralement la
moyenne, ou l’espérance, de la fonction d’erreur 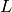 :
:
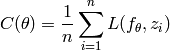
(c’est ce que l’on appelle l’erreur d’entraînement), ou

(c’est l’erreur de généralisation). En apprentissage supervisé, on a
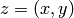 , et
, et 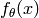 est une prédiction de
est une prédiction de 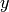 ,
indexée par les paramètres
,
indexée par les paramètres  .
.
Le gradient¶
Le gradient de la fonction  par rapport à un scalaire
par rapport à un scalaire  est défini formellement comme suit :
est défini formellement comme suit :
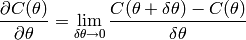
C’est-à-dire que c’est la variation 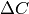 provoquée par un
changement
provoquée par un
changement 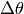 , dans la limite où
, dans la limite où 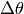 est très petit.
est très petit.
Lorsque  est un vecteur, le gradient
est un vecteur, le gradient
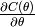 est un vecteur, contenant un élément
est un vecteur, contenant un élément
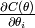 pour chaque
pour chaque  , en considérant les autres paramètres fixés :
on fait le changement
, en considérant les autres paramètres fixés :
on fait le changement 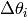 , et on mesure le
, et on mesure le
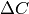 résultant. Lorsque
résultant. Lorsque 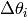 est petit, alors
est petit, alors
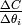 devient
devient
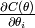 .
.
Descente de gradient¶
Nous voulons trouver une valeur de  qui minimise
qui minimise
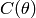 . Si nous arrivons à résoudre
. Si nous arrivons à résoudre
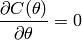
alors nous pouvons trouver les minimums (et les maximums, et les points de
selle), mais généralement nous ne sommes pas capables de trouver les solutions
de cette équation, donc nous utilisons des méthodes numériques d’optimisation.
La plupart de ces méthodes reposent sur l’idée de la descente locale :
on modifie itérativement  pour diminuer
pour diminuer 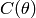 ,
jusqu’à ce que ça devienne impossible, c’est-à-dire que nous sommes arrivés à
un minimum local (et peut-être global, avec de la chance).
,
jusqu’à ce que ça devienne impossible, c’est-à-dire que nous sommes arrivés à
un minimum local (et peut-être global, avec de la chance).
La technique la plus simple, parmi les techniques d’optimisation à base de gradient, est la descente de gradient. Il existe de nombreuses variantes de descente de gradient, commençons par la descente de gradient ordinaire :
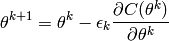
où 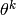 représente nos paramètres à l’itération
représente nos paramètres à l’itération 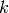 , et
, et
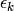 est un scalaire appelé pas de gradient (learning
rate), qui peut être fixé, adaptatif, ou déterminé par un échéancier
(schedule).
est un scalaire appelé pas de gradient (learning
rate), qui peut être fixé, adaptatif, ou déterminé par un échéancier
(schedule).
Descente de gradient stochastique¶
Pour la descente de gradient stochastique, nous exploitons le fait que
 est une moyenne sur des exemples généralement i.i.d. (indépendants
et identiquement distribués) pour faire des mises à jour de
est une moyenne sur des exemples généralement i.i.d. (indépendants
et identiquement distribués) pour faire des mises à jour de  de
manière beaucoup plus fréquente, à la limite (et dans le cas le plus commun)
après chaque exemple :
de
manière beaucoup plus fréquente, à la limite (et dans le cas le plus commun)
après chaque exemple :
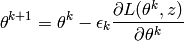
où  est le prochain exemple dans l’ensemble d’entraînement, ou le
prochain exemple tiré de la distribution d’entraînement dans le cas en
ligne (online) (où l’on n’a pas accès à un ensemble d’entraînement de
taille fixe, mais à un flux d’exemples provenant d’un processus de génération
de données).
est le prochain exemple dans l’ensemble d’entraînement, ou le
prochain exemple tiré de la distribution d’entraînement dans le cas en
ligne (online) (où l’on n’a pas accès à un ensemble d’entraînement de
taille fixe, mais à un flux d’exemples provenant d’un processus de génération
de données).
La descente de gradient stochastique (stochastic gradient descent, SGD) est un principe plus général, dans lequel la direction de la mise à jour est une variable aléatoire, dont l’espérance est le véritable gradient qui nous intéresse. Les conditions de convergence de la SGD sont similaires à celles de la descente de gradient, malgré la plus grande quantité de hasard.
La SGD peut être beaucoup plus rapide que la descente de gradient ordinaire (batch), parce que le nombre de mises à jour est beaucoup plus grand. C’est particulièrement vrai pour des jeux de données volumineux, ou pour le cas en ligne. En fait, dans les tâches d’apprentissage machine, on n’utilise la descente de gradient ordinaire (au lieu de stochastique) que lorsque la fonction à minimiser ne peut pas être décomposée comme ci-dessus (comme une moyenne).
Descente de gradient stochastique par mini-lots¶
C’est une variante de la SGD, dans laquelle on obtient la direction de la mise
à jour en prenant la moyenne de l’erreur sur un petit nombre d’exemples
(mini-lot, ou minibatch) 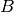 (par exemple, 10, 20 ou 100).
L’avantage principal est qu’au lieu d’effectuer
(par exemple, 10, 20 ou 100).
L’avantage principal est qu’au lieu d’effectuer 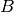 produits
vecteur-matrice, on peut souvent faire un produit matrice-matrice, la première
matrice ayant
produits
vecteur-matrice, on peut souvent faire un produit matrice-matrice, la première
matrice ayant 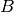 rangées, ce qui peut être implémenté de façon beaucoup
plus efficace (parfois 2 à 10 fois plus rapide, selon la taille des matrices).
rangées, ce qui peut être implémenté de façon beaucoup
plus efficace (parfois 2 à 10 fois plus rapide, selon la taille des matrices).
La SGD par mini-lots a l’avantage de travailler avec un estimé du gradient qui
est moins bruité (de moins en moins bruité lorsque 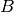 augmente). Par
contre, lorsque la taille du lot augmente, le nombre de mises à jour diminue
par rapport au nombre de calculs faits (à la limite, cela devient très
inefficace, autant que la descente de gradient ordinaire).
Il y a un compromis optimal (en terme d’efficacité computationnelle), qui peut
varier selon la distribution des données et les particularités de la classe de
fonctions considérée, ainsi que de la manière dont les calculs sont réalisés
(l’architecture matérielle et le parallélisme peuvent faire une différence).
augmente). Par
contre, lorsque la taille du lot augmente, le nombre de mises à jour diminue
par rapport au nombre de calculs faits (à la limite, cela devient très
inefficace, autant que la descente de gradient ordinaire).
Il y a un compromis optimal (en terme d’efficacité computationnelle), qui peut
varier selon la distribution des données et les particularités de la classe de
fonctions considérée, ainsi que de la manière dont les calculs sont réalisés
(l’architecture matérielle et le parallélisme peuvent faire une différence).
Inertie (momentum)¶
Une autre variation, dont l’esprit est similaire à celui de la SGD par mini-lots, est l’utilisation d’un terme dit d’inertie (momentum): l’idée est de calculer à la volée une moyenne mobile des gradients précédents, et d’utiliser cette moyenne mobile, et non le gradient de l’exemple courant, dans la formule de mise à jour. La moyenne mobile est généralement une moyenne mobile exponentielle :
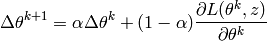
où 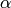 est un hyper-paramètre contrôlant le poids relatif des
gradients plus ancients par rapport aux plus récents.
est un hyper-paramètre contrôlant le poids relatif des
gradients plus ancients par rapport aux plus récents.
Choisir l’échéancier du pas de gradient¶
Si le pas de gradient est trop grand – plus grand que le double de la plus
grande valeur propre de la dérivée seconde (hessienne) de  –, alors
les mises à jour font augmenter le coût au lieu de le diminuer. Si le pas de
gradient est trop petit, la convergence est plus lente.
–, alors
les mises à jour font augmenter le coût au lieu de le diminuer. Si le pas de
gradient est trop petit, la convergence est plus lente.
Les choix d’échéancier du pas de gradient (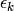 ) sont les
suivants:
) sont les
suivants:
Valeur constante,
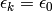 : c’est le choix le plus
commun. En théorie, il donne un poids exponentiellement plus grand aux
exemples les plus récents, et il est particulièrement adapté dans un
environnement non stationnaire, où la distribution peut changer.
Il est très robuste, mais l’erreur arrête de diminué après un certain temps,
alors qu’un pas de gradient plus petit pourrait donner une solution plus
précise (s’approcher un peu plus du minimum).
: c’est le choix le plus
commun. En théorie, il donne un poids exponentiellement plus grand aux
exemples les plus récents, et il est particulièrement adapté dans un
environnement non stationnaire, où la distribution peut changer.
Il est très robuste, mais l’erreur arrête de diminué après un certain temps,
alors qu’un pas de gradient plus petit pourrait donner une solution plus
précise (s’approcher un peu plus du minimum).Diminution en
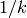 :
:
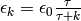 .
Il est garanti que cet échéancier arrivera à converger asymptotiquement
(lorsque
.
Il est garanti que cet échéancier arrivera à converger asymptotiquement
(lorsque 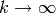 ), car il satisfait aux conditions
suivantes :
), car il satisfait aux conditions
suivantes :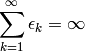
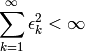
Cette garantie est vraie quel que soit
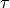 , mais
, mais 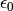 doit être assez petit pour éviter de diverger (lorsque l’erreur augmente au
lieu de diminuer).
doit être assez petit pour éviter de diverger (lorsque l’erreur augmente au
lieu de diminuer).Un des inconvénients est l’ajout d’un nouvel hyper-paramètre
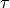 .
Un autre problème est que, malgré les garanties, un mauvais choix de
.
Un autre problème est que, malgré les garanties, un mauvais choix de
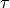 peut entraîner une convergence très lente.
peut entraîner une convergence très lente.
Graphes de flot, dérivée en chaîne et rétropropagation : calcul efficace du gradient¶
Considérons une fonction (dans notre cas, ce sera 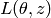 ) de
plusieurs arguments, nous voulons calculer sa valeur, ainsi que celle de sa
dérivée (son gradient) par rapport à certains de ses arguments. Nous allons
décomposer le calcul de la fonction en termes de calculs élémentaires, pour
lesquels les dérivées partielles sont faciles à calculer, formant ainsi un
graphe de flot (comme déjà mentionné ici).
Un graphe de flot est un graphe dirigé acyclique, où chaque nœud représente le
résultat d’un calcul qui est effectué sur les valeurs associées aux nœuds du
graphe qui lui sont connectés. Le graphe a des nœuds d’entrée (sans
prédécesseurs), et des nœuds de sortie (sans sucesseurs).
) de
plusieurs arguments, nous voulons calculer sa valeur, ainsi que celle de sa
dérivée (son gradient) par rapport à certains de ses arguments. Nous allons
décomposer le calcul de la fonction en termes de calculs élémentaires, pour
lesquels les dérivées partielles sont faciles à calculer, formant ainsi un
graphe de flot (comme déjà mentionné ici).
Un graphe de flot est un graphe dirigé acyclique, où chaque nœud représente le
résultat d’un calcul qui est effectué sur les valeurs associées aux nœuds du
graphe qui lui sont connectés. Le graphe a des nœuds d’entrée (sans
prédécesseurs), et des nœuds de sortie (sans sucesseurs).
Chaque nœud du graphe de flot est associé à une expression symbolique, qui
définit comment sa valeur est calculée à partir des valeurs de ses enfants
(les nœuds qui lui servent d’entrées). Nous nous concentrerons sur
l’utilisation des graphes de flot pour un calcul efficace du gradient, plus
particulièrement du gradient d’un nœud de sortie particulier, scalaire (noté
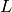 ici, on s’intéresse au gradient d’une fonction d’erreur par rapport
aux paramètres). À chaque nœud, nous associerons :
ici, on s’intéresse au gradient d’une fonction d’erreur par rapport
aux paramètres). À chaque nœud, nous associerons :
- la valeur du nœud,
- l’expression symbolique qui spécifie comment calculer la valeur du nœud à partir des valeurs de ses prédécesseurs (ses enfants),
- la dérivée partielle de
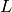 par rapport à la valeur du nœud,
par rapport à la valeur du nœud, - l’expression symbolique qui spécifie comment calculer la valeur de cette dérivée partielle, à partir des valeurs de ses prédécesseurs.
Soit 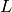 le nœud de sortie scalaire du graphe de flot, considérons un
nœud arbitraire
le nœud de sortie scalaire du graphe de flot, considérons un
nœud arbitraire 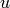 , dont les parent (les nœuds qui
prennent comme entrée la valeur calculée par
, dont les parent (les nœuds qui
prennent comme entrée la valeur calculée par 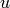 ) sont
) sont 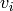 .
En plus de la valeur
.
En plus de la valeur 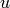 (c’est un abus de notation) associée au nœud
(c’est un abus de notation) associée au nœud
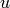 , nous allons aussi associer à chaque nœud
, nous allons aussi associer à chaque nœud 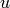 une dérivée
partielle :
une dérivée
partielle : 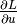 .
.
La règle de dérivation en chaîne spécifie comment la dérivée partielle
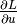 pour un nœud
pour un nœud 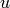 peut être
obtenue, de manière récursive, à partir des dérivées partielles
peut être
obtenue, de manière récursive, à partir des dérivées partielles
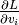 pour ses parents
pour ses parents 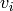 :
:
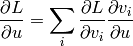
Notons que la récursion commence à 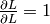 ,
pour le nœud racine du graphe (dans le cas général, c’est bien un graphe et
non un arbre, car il peut y avoir plusieurs chemins entre un nœud donné et le
nœud racine, ou sortie).
Notons aussi que chaque
,
pour le nœud racine du graphe (dans le cas général, c’est bien un graphe et
non un arbre, car il peut y avoir plusieurs chemins entre un nœud donné et le
nœud racine, ou sortie).
Notons aussi que chaque 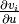 est une
expression (à laquelle correspond une valeur, lorsque les valeurs d’entrée
sont données) associée à un arc du graphe (et chaque arc est associé à
une dérivée partielle de ce type).
est une
expression (à laquelle correspond une valeur, lorsque les valeurs d’entrée
sont données) associée à un arc du graphe (et chaque arc est associé à
une dérivée partielle de ce type).
On remarque que les calculs de gradient utilisés dans cette méthode vont
exactement dans le sens opposé des calculs utilisés pour calculer 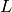 .
En fait, on dit que les gradients sont rétropropagés, en suivant les
arcs dans le sens inverse. L’utilisation de cette procédure pour calculer
le gradient dans le cas de réseaux de neurones (sans récurrence) multi-couches
est appelée l’algorithme de la rétropropagation du gradient.
.
En fait, on dit que les gradients sont rétropropagés, en suivant les
arcs dans le sens inverse. L’utilisation de cette procédure pour calculer
le gradient dans le cas de réseaux de neurones (sans récurrence) multi-couches
est appelée l’algorithme de la rétropropagation du gradient.
Dans l’exemple vu plus tôt, 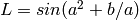 , et il y
a deux chemins de
, et il y
a deux chemins de  vers
vers 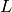 .
.
Cette méthode nous donne certaines garanties. Si le calcul de 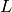 s’exprime par
s’exprime par 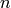 calculs, matérialisés par
calculs, matérialisés par 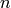 nœuds (et que
le calcul chaque nœud requiert un temps constant) et
nœuds (et que
le calcul chaque nœud requiert un temps constant) et 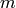 arcs, alors
le calcul de toutes les dérivées partielles
arcs, alors
le calcul de toutes les dérivées partielles
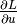 requiert (au plus)
requiert (au plus) 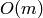 calculs,
en utilisant la récursion ci-dessus (en général, le nombre d’entrées d’un nœud
est borné, et c’est aussi
calculs,
en utilisant la récursion ci-dessus (en général, le nombre d’entrées d’un nœud
est borné, et c’est aussi 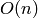 ).
De plus, c’est aussi une borne inférieure, c’est-à-dire qu’il n’est pas
possible de calculer le gradient plus vite (à une constante additive et
multiplicative près).
).
De plus, c’est aussi une borne inférieure, c’est-à-dire qu’il n’est pas
possible de calculer le gradient plus vite (à une constante additive et
multiplicative près).
Notons enfin qu’il existe de nombreuses manières de calculer ces gradients, et
qu’alors que l’algorithme ci-dessus est le plus rapide, il est facile d’écrire
une récursion, apparemment simple, qui serait exponentiellement plus lente,
c’est-à-dire en 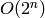 . De manière générale,
. De manière générale,
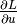 peut être écrite comme la somme, sur
tous les chemins du graphe de
peut être écrite comme la somme, sur
tous les chemins du graphe de 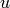 à
à 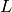 , du produit des dérivées
partielles selon chaque chemin.
, du produit des dérivées
partielles selon chaque chemin.
Illustrons cela avec un graphe qui a la structure suivante :
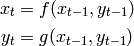
où il existe 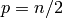 paires de nœuds
paires de nœuds 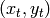 , terminant par
, terminant par
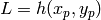 , et dont les nœuds d’entrée sont
, et dont les nœuds d’entrée sont 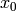 et
et
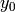 .
Le nombre de chemins de
.
Le nombre de chemins de 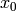 à
à 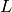 est
est
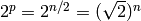 . Par construction, à chaque fois que
l’on ajoute une paire de nœuds, le nombre de chemins est doublé.
. Par construction, à chaque fois que
l’on ajoute une paire de nœuds, le nombre de chemins est doublé.