Introduction rapide à l’apprentissage machine pour l’IA¶
Les sujets abordés ici sont couverts dans cette présentation.
Intelligence¶
La notion d’intelligence peut être définie de bien des façons. Ici, nous la définissons comme la capacité de prendre la bonne décision, selon un certain critère (par exemple, survivre et se reproduire, pour la plupart des animaux). Pour prendre de meilleures décisions, des connaissances sont nécessaires, et elles doivent être dans un format opérationnel: elles doivent pouvoir être utilisées pour interpréter des données sensorielles et prendre des bonnes décisions en conséquence.
Intelligence artificielle¶
Les ordinateurs possèdent déjà certaines formes d’intelligence, grâce à des programmes, créés par les humains, qui leur permettent de « faire des choses » considérées utiles (nous considérons généralement la bonne décision comme celle qui est la plus utile). Cependant, il existe de nombreuses tâches faciles à réaliser pour des animaux ou des humains, mais qui restent hors d’atteinte pour les ordinateurs, au début du 21 e siècle. La plupart de ces tâches font partie de ce que l’on appelle l’intelligence artificielle (IA), ce qui inclut les tâches de perception et de contrôle. Comment se fait-il que nous n’ayons pas réussi à écrire de programmes réalisant ces tâches ? Je crois que la principale raison est que nous ne savons pas explicitement (de façon formelle) comment résoudre ces tâches, même si notre cerveau (avec notre corps) est capable de les réaliser de façon instinctive. Les connaissances permettant de réaliser ces tâches sont actuellement implicites, mais nous avons des informations, des données qui nous viennent d’exemples (par exemple, des observations de ce qu’un humain ferait dans certaines situations, étant donné un but). Comment faire pour que des machines puissent acquérir ce genre d’intelligence ? Par l’apprentissage, c’est-à-dire l’utilisation de données et d’exemples pour construire des connaissances opérationnelles.
Apprentissage machine¶
L’apprentissage machine (ou machine learning, ML) a une longue histoire, et de nombreux manuels couvrent ses principes. Parmi les manuels récents, je suggère :
- Christopher M. Bishop, *Pattern Recognition and Machine Learning*, 2007
- Simon Haykin, *Neural Networks: a Comprehensive Foundation*, 2009 (3rd edition)
- Richard O. Duda, Peter E. Hart and David G. Stork, *Pattern Classification*, 2001 (2nd edition)
Ici, nous allons nous concentrer sur certains concepts, qui sont les plus pertinents pour ce cours.
Formaliser l’apprentissage¶
Voici d’abord le formalisme mathématique le plus fréquemment utilisé pour décrire l’apprentissage. Nous disposons d’exemples d’entraînement
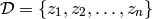
où les 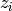 sont des exemples générés par un processus inconnu
sont des exemples générés par un processus inconnu
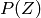 .
.
Nous avons également une fonction d’erreur 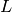 , qui prend comme arguments
une fonction de décision
, qui prend comme arguments
une fonction de décision 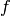 et un exemple
et un exemple  , et qui renvoie un
scalaire réel. Nous voulons minimizer l’espérance de
, et qui renvoie un
scalaire réel. Nous voulons minimizer l’espérance de 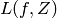 sous le
processus stochastique
sous le
processus stochastique 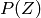 .
.
Apprentissage supervisé¶
Dans l’apprentissage supervisé, chaque exemple est une paire (entrée, cible):
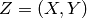 , et
, et 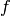 s’applique à des exemples de
s’applique à des exemples de 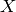 .
Les deux exemples de problèmes supervisés les plus fréquents sont
.
Les deux exemples de problèmes supervisés les plus fréquents sont
La régression :
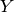 est un réel, ou un vecteur de réels, la sortie de
est un réel, ou un vecteur de réels, la sortie de
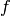 est dans le même espace que
est dans le même espace que 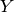 , et l’erreur est
souvent l’erreur quadratique:
, et l’erreur est
souvent l’erreur quadratique: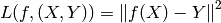
La classification:
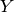 est un entier fini (c’est-à-dire un symbole),
qui correspond à l’indice d’une classe, et la fonction d’erreur utilisée est
souvent la log-vraisemblance conditionnelle négative, en interprétant
est un entier fini (c’est-à-dire un symbole),
qui correspond à l’indice d’une classe, et la fonction d’erreur utilisée est
souvent la log-vraisemblance conditionnelle négative, en interprétant
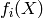 comme une estimation de
comme une estimation de 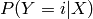 :
: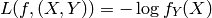
avec les contraintes suivantes:
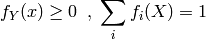
Apprentissage non supervisé¶
Dans l’apprentissage non supervisé, nous apprenons une fonction 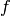 qui
aide à caractériser une distribution inconnue
qui
aide à caractériser une distribution inconnue 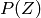 .
. 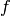 peut
être un estimateur de
peut
être un estimateur de 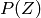 directement (estimation de densité). Dans
d’autre cas,
directement (estimation de densité). Dans
d’autre cas, 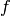 essaie d’estimer les zones où la densité de probabilité
se concentre.
essaie d’estimer les zones où la densité de probabilité
se concentre.
Les algorithmes de partitionnement (clustering) divisent l’espace des
entrées en différentes régions (souvent autour d’un exemple “prototype”, ou
d’un centroïde). Certains algorithmes de partitionnement créent des partitions
“dures” (par exemple, l’algorithme des k moyennes, ou k-means), où chaque
exemple appartient seulement à une région. D’autres construisent une partition
“douce” (soft) (par exemple, un mélange de gaussiennes), qui assigne à
chaque 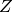 une probabilité d’appartenir à chaque cluster.
une probabilité d’appartenir à chaque cluster.
D’autres algorithmes non supervisés apprennent une transformation
qui construit une nouvelle représentation pour 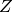 . Beaucoup
d’algorithmes d’apprentissage profonds appartiennent à cette
catégorie, l’analyse en composantes principales (ACP, ou principal
components analysis, PCA) également.
. Beaucoup
d’algorithmes d’apprentissage profonds appartiennent à cette
catégorie, l’analyse en composantes principales (ACP, ou principal
components analysis, PCA) également.
Généralisation locale¶
La grande majorité des algorithmes d’apprentissage exploitent un seul
principe pour généraliser : la généralisation locale. Par exemple,
un tel algorithme suppose que si un exemple d’entrée 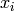 est
proche d’un autre exemple
est
proche d’un autre exemple 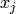 , alors les sorties correspondantes
, alors les sorties correspondantes
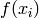 et
et 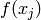 doivent aussi être proches. Ce principe est
utilisé pour l’interpolation locale.
doivent aussi être proches. Ce principe est
utilisé pour l’interpolation locale.
Ce principe est très puissant, mais il a ses limitations: et si on essaie d’extrapoler ? ou si la fonction inconnue (cible) a beaucoup plus de variations que le nombre d’exemples d’entraînement? Dans ce cas, il est impossible que la généralisation locale fonctionne, puisqu’il nous faut au moins autant d’exemples que de creux et de bosses dans la fonction cible pour couvrir toutes ces variations et généraliser par ce principe.
Ce problème est lié à ce que l’on appelle la malédiction de la
dimensionalité (ou fléau de la dimension, curse of dimensionality).
Lorsque l’espace des entrées est de haute dimension, le nombre de variations
de la fonction d’intérêt peut facilement être une fonction exponentielle du
nombre de dimensions d’entrée. Par exemple, imaginons que nous voulons
distinguer 10 valeurs différentes pour chaque variable d’entrée (chaque
élément du vecteur d’entrées), et que les 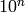 configurations de ces
configurations de ces
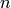 variables sont importantes ou nous intéressent. En utilisant
uniquement la généralisation locale, nous avons besoin d’au moins un exemple
pour chacune de ces
variables sont importantes ou nous intéressent. En utilisant
uniquement la généralisation locale, nous avons besoin d’au moins un exemple
pour chacune de ces 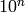 configurations pour pouvoir généraliser dans
chacune d’elles.
configurations pour pouvoir généraliser dans
chacune d’elles.
Représentations locales ou distribuées, généralisation non locale¶
Un entier 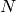 peut être représenté par une séquence de
peut être représenté par une séquence de 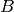 bits,
avec
bits,
avec 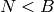 , telle que tous les bits valent 0 sauf le
, telle que tous les bits valent 0 sauf le 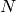 -ième.
C’est une représentation binaire locale.
Le même entier peut être représenté par une séquence de
-ième.
C’est une représentation binaire locale.
Le même entier peut être représenté par une séquence de
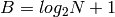 bits, qui contient la représentation habituelle
de
bits, qui contient la représentation habituelle
de 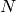 en base 2. Cette représentation binaire est distribuée.
Cet exemple nous montre qu’une représentation distribuée peut être
plus efficace qu’une représentation locale, et ce, de manière
exponentielle. De manière générale, pour les algorithmes
d’apprentissage, les représentations distribuées ont la capacité de
capturer “exponentiellement” plus de variations que les représentations
locales, pour le même nombre de paramètres libres.
Ainsi, ils ont le potentiel d’une meilleure généralisation, puisque la
théorie de l’apprentissage montre que le nombre d’exemples requis (pour
atteindre un certain degré de performance en généralisation) pour ajuster
en base 2. Cette représentation binaire est distribuée.
Cet exemple nous montre qu’une représentation distribuée peut être
plus efficace qu’une représentation locale, et ce, de manière
exponentielle. De manière générale, pour les algorithmes
d’apprentissage, les représentations distribuées ont la capacité de
capturer “exponentiellement” plus de variations que les représentations
locales, pour le même nombre de paramètres libres.
Ainsi, ils ont le potentiel d’une meilleure généralisation, puisque la
théorie de l’apprentissage montre que le nombre d’exemples requis (pour
atteindre un certain degré de performance en généralisation) pour ajuster
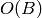 degrés de liberté effectifs est
degrés de liberté effectifs est 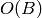 .
.
La différence entre les représentations locales et distribuées peut
aussi être illustrée par la différence entre le partitionnement
traditionnel, local, et l’analyse en composantes principales, ou les
machines de Boltzmann restreintes (restricted Boltzmann machines,
RBM), qui définissent des représentations distribuées.
Par exemple, k-means a besoin d’un vecteur de coordonnées pour chaque
prototype (centroïde), c’est-à-dire un vecteur pour chacune des régions
distinguées par l’algorithme. L’ACP, au contraire, représente la distribution
en gardant les directions où les variations sont les plus grande.
Imaginons une interprétation simplifiée de l’ACP, où tout ce qui nous intéresse,
pour chaque direction de variation, est de savoir si la projection de la
donnée est au-dessus (ou en-dessous) d’un certain seuil. Avec 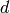 directions, on peut distinguer
directions, on peut distinguer 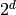 régions.
De la même manière les RBMs définissent
régions.
De la même manière les RBMs définissent 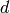 hyperplans, et
un bit indique si l’entrée est d’un côté ou de l’autre de chaque
hyperplan. Ainsi, une RBM associe une région de l’espace des entrées à chaque
configuration des bits de représentation (dans le vocabulaire des réseaux de
neurones, ces bits correspondent à des unités cachées). Le nombre de
paramètres d’une RBM est environ le nombre de ces bits multiplié par le
nombre de dimensions de l’entrée.
hyperplans, et
un bit indique si l’entrée est d’un côté ou de l’autre de chaque
hyperplan. Ainsi, une RBM associe une région de l’espace des entrées à chaque
configuration des bits de représentation (dans le vocabulaire des réseaux de
neurones, ces bits correspondent à des unités cachées). Le nombre de
paramètres d’une RBM est environ le nombre de ces bits multiplié par le
nombre de dimensions de l’entrée.
Nous pouvons voir que le nombre de régions définies par une RBM, ou l’ACP, c’est-à-dire des représentations distribuées, croît selon l’exponentielle du nombre de paramètres, alors que le nombre de régions définies par des algorithmes de partitionnement traditionnel (par exemple k-means, ou des mélanges de gaussiennes), qui définissent des représentations locales, croît linéairement avec le nombre de paramètres. Nous pouvons aussi voir que la RBM peut généraliser à une nouvelle région, c’est-à-dire à une configuration des ses unités cachées, dans laquelle il n’y avait aucun exemple d’entraînement. C’est quelque chose qui n’est pas possible pour les algorithmes de partitionnement classiques (ces algorithmes pourraient seulement généraliser localement de façon triviale, en répétant ce qu’ils ont appris dans les régions voisines contenant des exemples d’entraînement).