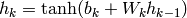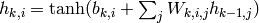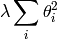Introduction to Multi-Layer Perceptrons (Feedforward Neural Networks)¶
Multi-Layer Neural Networks¶
An MLP (for Multi-Layer Perceptron) or multi-layer neural network defines
a family of functions. Let us first consider the most classical case
of a single hidden layer neural network, mapping a
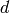 -vector to an
-vector to an 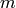 -vector (e.g. for regression):
-vector (e.g. for regression):
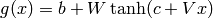
where:
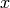 is a
is a 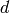 -vector (the input),
-vector (the input),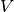 is an
is an  matrix (called input-to-hidden weights),
matrix (called input-to-hidden weights), is a
is a 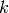 -vector (called hidden units offsets or hidden unit biases),
-vector (called hidden units offsets or hidden unit biases),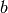 is an
is an 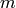 -vector (called output units offset or output units biases),
-vector (called output units offset or output units biases),- and
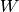 is an
is an 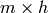 matrix (called hidden-to-output weights).
matrix (called hidden-to-output weights).
The vector-valued function 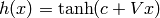 is called
the output of the hidden layer. Note how the output is an affine
transformation of the hidden layer, in the above network. A non-linearity
may be tacked on to it in some network architectures.
The elements of the hidden layer are called hidden units.
is called
the output of the hidden layer. Note how the output is an affine
transformation of the hidden layer, in the above network. A non-linearity
may be tacked on to it in some network architectures.
The elements of the hidden layer are called hidden units.
The kind of operation computed by the above 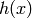 can be
applied on
can be
applied on 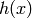 itself, but with different parameters
(different biases and weights). This would give rise to a
feedforward multi-layer network with two hidden layers. More generally,
one can build a deep neural network by stacking more such layers.
Each of these layers may have a different dimension (
itself, but with different parameters
(different biases and weights). This would give rise to a
feedforward multi-layer network with two hidden layers. More generally,
one can build a deep neural network by stacking more such layers.
Each of these layers may have a different dimension (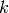 above).
A common variant is to have skip connections, i.e., a layer can take as
input not only the layer at the previous level but also some of the lower layers.
above).
A common variant is to have skip connections, i.e., a layer can take as
input not only the layer at the previous level but also some of the lower layers.
Most Common Training Criteria and Output Non-Linearities¶
Let 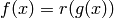 with
with  representing the output non-linearity function.
In supervised learning, the output
representing the output non-linearity function.
In supervised learning, the output 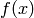 can be compared with
a target value
can be compared with
a target value 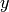 through a loss functional
through a loss functional 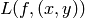 .
Here are common loss functionals, with the associated output non-linearity:
.
Here are common loss functionals, with the associated output non-linearity:
- for ordinary (L2) regression: no non-linearity (
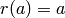 ), squared loss
), squared loss
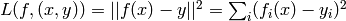 .
. - for median (L1) regression: no non-linearity (
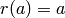 ), absolute value
loss
), absolute value
loss 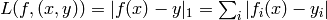 .
. - for 2-way probabilistic classification: sigmoid non-linearity
(
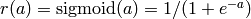 , applied element by element),
and cross-entropy loss
, applied element by element),
and cross-entropy loss 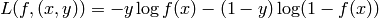 for
for 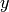 binary. Note that the sigmoid output
binary. Note that the sigmoid output 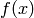 is in the (0,1) interval,
and corresponds to an estimator of
is in the (0,1) interval,
and corresponds to an estimator of 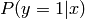 . The predicted
class is 1 if
. The predicted
class is 1 if 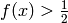 .
. - for multiple binary probabilistic classification: each output element is treated as above.
- for 2-way hard classification with hinge loss: no non-linearity (
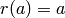 )
and the hinge loss is
)
and the hinge loss is 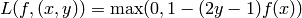 (again for
binary
(again for
binary  ). This is the SVM classifier loss.
). This is the SVM classifier loss. - the above can be generalized to multiple classes by separately considering the binary classifications of each class against the others.
- multi-way probabilistic classification: softmax non-linearity
(
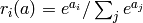 with one output per class)
with the negative log-likelihood
loss
with one output per class)
with the negative log-likelihood
loss 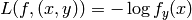 . Note that
. Note that 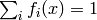 and
and 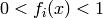 . Note also how this is equivalent to the cross-entropy
loss in the 2-class case (the output for the one of the classes is actually
redundant).
. Note also how this is equivalent to the cross-entropy
loss in the 2-class case (the output for the one of the classes is actually
redundant).
The Back-Propagation Algorithm¶
We just apply the recursive gradient computation algorithm seen previously to the graph formed naturally by the MLP, with one node for each input unit, hidden unit and output unit. Note that each parameter (weight or bias) also corresponds to a node, and the final
Let us formalize a notation for MLPs with more than one hidden layer.
Let us denote with 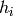 the output vector of the i-th layer,
starting with
the output vector of the i-th layer,
starting with 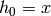 (the input), and finishing with
a special output layer
(the input), and finishing with
a special output layer 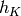 which produces the
prediction or output of the network.
which produces the
prediction or output of the network.
With tanh units in the hidden layers, we have (in matrix-vector notation):
- for
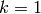 to
to 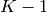 :
:
where
is a vector of biases and
is a matrix of weights connecting layer
to layer
. The scalar computation associated with a single unit
of layer
is
In the case of a probabilistic classifier, we would then have a softmax output layer, e.g.,
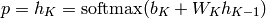
where we used 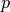 to denote the output because it is a vector indicating
a probability distribution over classes. And the loss is
to denote the output because it is a vector indicating
a probability distribution over classes. And the loss is
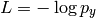
where 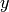 is the target class, i.e., we want to maximize
is the target class, i.e., we want to maximize 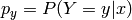 , an
estimator of the conditional probability of class
, an
estimator of the conditional probability of class 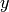 given input
given input 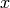 .
.
Let us now see how the recursive application of the chain rule in flow graphs is instantiated in this structure. First of all, let us denote
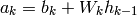
(for the argument of the non-linearity at each level) and note (from a small derivation) that
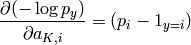
and that
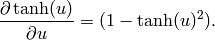
Now let us apply the back-propagation recipe in the corresponding flow graph. Each parameter (each weight and
each bias) is a node, each neuron potential 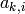 and each neuron output
and each neuron output 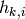 is also a node.
is also a node.
starting at the output node:
then compute the gradient with respect to each pre-softmax sum
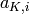 :
: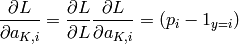
We can now repeat the same recipe for each layer. For
 down to 1:
down to 1:obtain trivially the gradient wrt biases:
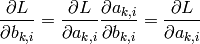
compute the gradient wrt weights:
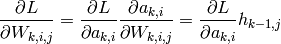
back-propagate the gradient into lower layer, if
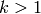 :
: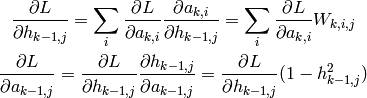
Logistic Regression¶
Logistic regression is a special case of the MLP with no hidden layer (the input is directly connected to the output) and the cross-entropy (sigmoid output) or negative log-likelihood (softmax output) loss. It corresponds to a probabilistic linear classifier and the training criterion is convex in terms of the parameters (which garantees that there is only one minimum, which is global).
Training Multi-Layer Neural Networks¶
Many algorithms have been proposed to train multi-layer neural networks but the most commonly used ones are gradient-based.
Two fundamental issues guide the various strategies employed in training MLPs:
- training as efficiently as possible, i.e., getting training error down as quickly as possible, avoiding to get stuck in narrow valleys or even local minima of the cost function,
- controlling capacity so as to achieve the largest capacity avoids overfitting, i.e., to minimize generalization error.
A fundamentally difficult optimization problem¶
Optimization of the training criterion of a multi-layer neural network is difficult because there are numerous local minima. It can be demonstrated that finding the optimal weights is NP-hard. However, we are often happy to find a good local minimum, or even just a sufficiently low value of the training criterion. Since what interests us is the generalization error and not just the training error (what we are minimizing is not what we would truly like to minimize), the difference between “close to a minimum” and “at a minimum” is often of no importance. Also, as there is no analytic solution to the minimization problem, we are forced to perform the optimization in an iterative manner.
Choice of architecture¶
In principle, one way of accelerating gradient descent is to make
choices which render the Hessian matrix
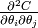 well conditioned. The second derivative in a certain direction
indicates he curvature of the cost function in that direction.
The larger the cuvature (as in narrow valleys), the smaller our
updates must be in order to avoid increasing the error. More
precisely, the optimal step size for a gradient step is 1 over
the curvature. This can be seen by a simple Taylor expansion of
the cost function, and is behind the famous optimization algorithm
known as Newton’s method. Suppose we are at
well conditioned. The second derivative in a certain direction
indicates he curvature of the cost function in that direction.
The larger the cuvature (as in narrow valleys), the smaller our
updates must be in order to avoid increasing the error. More
precisely, the optimal step size for a gradient step is 1 over
the curvature. This can be seen by a simple Taylor expansion of
the cost function, and is behind the famous optimization algorithm
known as Newton’s method. Suppose we are at 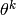 and we wish to choose
and we wish to choose 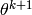 such that it is a minimum:
such that it is a minimum:
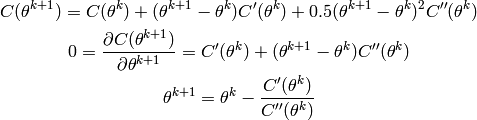
Thus, we want a step size equal to the inverse of the second derivative. One can show that the number of iterations of a gradient descent algorithm will be proportional to the ratio of the largest to the smallest eigenvalue of the Hessian matrix (with a quadratic approximation of the cost function). The basic reason is that the largest eigenvalue limits the maximum step size. One cannot go faster than the highest curvature in all possible directions, otherwise the error will increase, but if we use the same step size in all directions, the convergence will be the slowest in the flattest direction (the direction corresponding to the smallest eigenvalue).
- In theory one hidden layer suffices, but this theorem does not say that this representation of the function will be efficient. In practice, this was the most common choice before 2006, with the exception of convolutional neural networks (which can have 5 or 6 hidden layers, for example). Sometimes one obtains much better results with two hidden layers. In fact, we obtain a much better generalization error with even more layesr, but a random initailization does not work well with more than two hidden layes (but see the work since 2006 on greedy unsupervised initialization for deep architectures).
- For regression or with real-valued targets that are not bounded, it is generally better to use linear neurons in the output layer. For classification, it is generally better to use neurons with a non-linearity (sigmoid or softmax) in the output layer.
- In certain cases, direct connections between the input and the output layer can be useful. In the case of regression, they can also be directly initialized by a linear regression of the outputs on the inputs. The hidden layer neurons then serve only to learn the missing non-linear part.
- An architecture with shared weights, or sharing certain parts of the architecture (e.g. the first layer) between networks associated with several related tasks, can significantly improve generalization. See the following discussion on convolutional networks.
- It is better to use a symmetric nonlinearity in the hidden layers (such as the hyperbolic tangent, or “tanh”, and unlike the logistic sigmoid), in order to improve the conditioning of the Hessian and avoid saturation of the nonlinearity in the hidden layers.
Normalizing the inputs¶
It is imperative that the inputs have a mean not too far from zero, and a variance not far from one. Values of the input must also not be too large in magnitude. If this is not the case, one can perform certain monotonic, non-linear transformation that reduce large values. If we have a very large input, it will saturate many neurons and block the learning algorithm for that example. The magnitudes (variances) of inputs to each layer must also be of the same order when using a single learning rate for all of the layers, in order to avoid one layer becoming a bottleneck (the slowest to train).
In fact, in the linear case, the Hessian is optimally conditioned when
the inputs are normalized (so that the covariance matrix is the identity),
which can be done by projecting into the eigenspace of the matrix 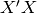 ,
where
,
where 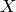 is the matrix where
is the matrix where 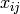 is input
is input 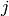 of
training example
of
training example 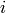 .
.
Preprocessing of the target outputs¶
In the case of learning by minimizing a quadratic cost function (e.g. mean squared error) it must be assured that the target outputs
are always in the interval of values that the nonlinearity in the output layer can produce (and are roughly normal N(0, 1) in the linear case)
are not too near to the limits of the nonlinearity in the output layer: for classification, an optimal value is close to the two inflection points (i.e., the points of maximal curvature/second derivative, -0.6 and 0.6 for tanh, 0.2 and 0.8 for sigmoid).
It is best to use the cross-entropy criterion (or conditional log likelihood) for probabilistic classification, or the “hinge” margin criterion (as is used for the perceptron and SVMs, but by penalizing departures from the decision surface beyond a margin). In the case of multiclass classification, this gives
where
is the “positive part” of
and
is the output (without a nonlinearity) for class
.
Coding of target outputs and discrete inputs¶
With inputs and outputs, we generally represent discrete variables
by groups of units (a group of 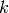 units for a discrete variable that
can take
units for a discrete variable that
can take 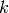 values). The practical exception is the case of a binary
variable, which we generally encode with a single unit. In the case of
outputs, we will associate with each group a discrete distribution (binomial
for a single bit, multinomial for a general discrete variable).
values). The practical exception is the case of a binary
variable, which we generally encode with a single unit. In the case of
outputs, we will associate with each group a discrete distribution (binomial
for a single bit, multinomial for a general discrete variable).
Optimization algorithms¶
When the number of examples is large (many thousands) stochastic gradient descent is often the best choice (especially for classification), in terms of speed and in terms of capacity control: it is more difficult for the network to overfit when training with stochastic gradient descent. Indeed, stochastic gradient descent does not fall easily into very sharp minima (which do not generalize well, since a slight perturbation of the data that changes the error surface will yield very bad performance) due to noise induced by gradient steps and the “noisy” gradient. This noisy gradient also helps to escape certain local minima for the same reason.
When stochastic gradient descent is used, it is critical that the examples be well mixed. For example if we have many consecutive examples of the same class, the convergence will be very slow. It is enough to randomly permute the examples once per training session, in oder to eliminate all dependence between successive examples. With certain architectures that capture temporal dependencies (music, speech, video or other time series) we have no choice but to present sequences whose elements are highly dependent, but we can mix up the sequences (the training set is a group of of sequences).
In principle, the gradient step size should be gradually reduced during
learning in order to guarantee asymptotic convergence. For certain problems
(especially classification), this does not seem necessary, and can even
hurt. A reasonable annealing schedule, for example, is
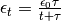 as discussed here.
If you could calculate it, the optimal gradient step would be
as discussed here.
If you could calculate it, the optimal gradient step would be
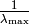 , i.e. the inverse of the largest
eigenvalue of the Hessian matrix, and the maximal step size (before
divergence) would be twice as large. Le Cun proposes an efficient method
for estimating
, i.e. the inverse of the largest
eigenvalue of the Hessian matrix, and the maximal step size (before
divergence) would be twice as large. Le Cun proposes an efficient method
for estimating 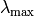 (see his tutorial on the subject)
but this technique is not often used.
(see his tutorial on the subject)
but this technique is not often used.
When the number of examples (and thus, of parameters) is very small, especially for regression, second order methods (often the conjugate gradient method) allow for much faster convergence. These methods are batch methods (updating parameters only after calculating the error and gradient on all examples). These tecniques are generally easier to use than stochastic gradient descent (there are less hyperparameters, or it is less necessary to modify them from the default values), but the generalization is often worse because of the ease with which such methods fall into sharp minima.
Up to several tens of thousands of training examples, conjugate gradient descent remains one of the best optimization techniques for neural networks. Beyond that, it is generally best to stick with stochastic gradient descent or the minibatch variant thereof.
Parameter initialization¶
We cannot initialize all the weights to zero without condemning all the hidden units to always computing the same thing (which can be seen by a simple symmetry argument). We would also like to avoid saturating units (outputs close to the limits of the non-linearity, such that the gradient is close to zero), while also avoiding units being too close initially to a linear function. When the parameters are too close to zero, a multilayer network calculates an affine (linear) transformation, so its effective capacity per output is the number of inputs plus one. Based on these considerations, the ideal operating regime of a unit would be close to the inflection point of the nonlinearity (between the linear part of the activation close to the origin and the saturating part). Also, we would like the average variance of the hidden unit values to be preserved when we propagate the “activations” from the output to the input, and in the same way we would like the variance of the gradients to be preserved as we propagate them backwards.
In order to achieve this objective, it can be argued that the initial
weights should be drawn uniformly from the interval
![[-\sqrt{6/(n_i + n_o)}, \sqrt{6/(n_i+n_o)}]](_images/math/ed5a95b9e8390dcef2e513353c64eb56ce033a14.png) , where
, where 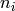 is the fan-in, i.e., the number of inputs to a neuron (the number
of neuons in the previous layer), and
is the fan-in, i.e., the number of inputs to a neuron (the number
of neuons in the previous layer), and 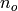 is the fan-out,
i.e., the number of neurons in the following layer. This supposes
that the inputs are approximately uniformly distributed in the
interval (-1,1) (note that the outputs of tanh hidden units fall in the
same interval).
is the fan-out,
i.e., the number of neurons in the following layer. This supposes
that the inputs are approximately uniformly distributed in the
interval (-1,1) (note that the outputs of tanh hidden units fall in the
same interval).
Controlling saturation¶
One frequent problem during learning is the saturation of neurons, often due to a bad normalization of inputs or target outputs or a bad initialization of weights, or using the logistic signmoid instead of a symmetric nonlinearity such as tanh. This can be controlled by observing the distribution of outputs of neurons (in particular, the mean of the absolute value of the weighted sum is a good indicator). When the neurons saturate frequently, learning is blocked on a plateau of the cost function due to the very small gradients on certain parameters (and thus a very badly conditioned Hessian).
Controlling the effective capacity¶
Vapnik’s theory of structural risk minimization tells us that there exists an optimal capacity around which the generalization error increases (i.e. there is a unique, global minimum of generalization error as a function of model capacity). Techniques for controlling the effective capacity thus seek to find this minimum (obviously in an approximate fashion):
early stopping: this is one of the most popular and most efficient techniques, but it does not work well when the number of examples is very small. The idea is very simple: we use a validation set of examples held out from training via gradient descent to estimate the generalization error as the iterative learning proceeds (normally, after each epoch we measure the error on the validation set). We keep the parameters corresponding to the minimum of this estimated generalization error curve (and we can stop when this error begins to seriously climb or if a better minimum is not found in a certain number of epochs). This has the advantage of responding to one of the difficult questions of optimization, that is: when do we stop? As well, we note that it is a cheap (in terms of computing time) way to choose an important hyperparameter (number of training iterations) that affects both optimization and generalization.
controlling the number of hidden units: This number directly influences the capacity. In this case we must unfortunately perform several experiments, unless you use a constructive learning algorithm which adds resources if and when they are needed), see for example the cascade-correlation algorithm (Fahlman, 1990). We can use a validation set or cross-validation to estimate the generalization error. One must be careful, as this estimate is noisy (especially if there are few examples in the validation set). When there are many hidden layers, choosing the same number of hidden units per layer seems to work well. The price paid in longer computation time for a larger number of hidden units (because of the increased number of parametes) is generally offset by early stopping. By contrast, when the number of hidden units is too small, the effect on the generalization error and the training error can be much larger. We generally choose the size of networks empirically, bearing in mind these consideration in order to avoid having to try too many different sizes.
weight decay: This is a regularization method (for controlling capacity, to prevent overfitting) where the aim is to penalize weights with large magnitude. Indeed, it can be shown that the capacity is bounded by the magnitude of the weights of a neural network. We add the penalty
to the cost function. This is known as L2 regularization, since it inimizes the L2 norm of the parameters. Sometimes this is applied only to the weights and not to biases.
As in the previous case, we must run several leaning experiments and choose the penalty parameter
(a hyperparameter) that minimizes the estimated generalization error. This can be estimated with a validation set or with cross-validation.
A form of regularization that is more and more used as an alternative to L2 regularization is L1 regularization, which has the advantage that small parameters will be shrunk to exactly 0, giving rise to a sparse vector of parameters. It thus minimizes the sum of the absolute values of the parameters (the L1 norm).