Arbre binaire de recherche
(référence: Chap. 10)
Un arbre binaire = un arbre qui a au plus 2 branches par nœud.
Un arbre binaire de recherche est un arbre binaire dans lequel chaque nœud et ses enfants suit la règle suivante: Les valeurs des nœuds enfants à gauche sont <= la valeur du nœud père, et les valeurs des nœuds enfants à droite sont > à la valeur du nœud père.
Structure de données pour un nœud
De façon générale, un nœud d'un arbre binaire correspond à la structure suivante:
class Noeud {
Object datum;
Noeud left, right;
int key() {...}
}
Dans Object datum, comme dans le cas de liste, on stocke toutes informations nécessaires pour une application (par exemple, les informations sur un étudiant). "left" et "right" pointent vers les enfants. S'il n'y a pas d'enfants, ils pointent vers "null". La méthode "key" détermine une clé selon datum. Cela peut être simplement un des attributs dans datum, ou bien une valeur calculée selon certains attributs de datum. De façon encore plus générale, on pourrait simplement exiger que key() retourne une valeur du type "Comparable". Mais pour simplifier, ici, on suppose que key retourne une valeur int.
Les opérations typiques sur un arbre binaire comprennent les suivantes:
Dans cette partie, nous commençons encore par la définition et les manipulations sur un arbre binaire concret. Ensuite, nous allons à un niveau d'abstraction plus élevé.
Un arbre binaire concret
Définissons un arbre simple dont chaque nœud contient une valeur d'entier comme datum. La clé utilisée pour organiser l'arbre est la même valeur. On a donc la déclaration de classe suivante:
class Noeud_Int {
int valeur;
Noeud_Int gauche, droite;
Noeud_Int () {}
Noeud_Int(int v, Noeud_Int g, Noeud_Int d) {
valeur = v;
gauche = g;
droite = d;
}
}
Utiliser la classe Nœud_Int pour un arbre
Comme dans le cas de liste, on peut aussi utiliser la racine de l'arbre comme identification de l'arbre. Ainsi, on n'a juste besoin de la classe Noeud_Int. Les opérations sur l'arbre seront intégrées dans cette même classe.
Voici quelques-unes unes de ces méthodes:
public void ajout(int v) {
if (valeur <= v) {
if (gauche == null) gauche = new Noeud_Int(v, null, null);
else gauche.ajout(v);
}
else {
if (droite == null) droite = new Noeud_Int(v, null, null);
else droite.ajout(v);
}
}
public int nombre_noeud() {
int nb_gauche, nb_droite;
if (gauche==null) nb_gauche = 0;
else nb_gauche = gauche.nombre_noeud();
if (droite==null) nb_ droite = 0;
else nb_ droite = droite.nombre_noeud();
return 1 + nb_gauche + nb_droite;
}
public Noeud_Int chercher(int v) {
if (valeur == v) return this;
else if (v < valeur) {
if (gauche == null) return null;
else return gauche.chercher(v);
}
else {
if (droite == null) return null;
else return droite.chercher(v);
}
}
public void imprimer_pre_ordre() {
System.out.println(valeur);
if (gauche != null) gauche.imprimer_pre_ordre();
if (droite != null) droite.imprimer_pre_ordre();
}
public Noeud_Int enlever(int v) {
// enlever un noeud contenant la valeur v, et retourne la racine de l'arbre/sous-arbre
if (v < valeur) {
if (gauche == null) return this;
else {
gauche = gauche.enlever(v);
return this;
}
}
else if (v > valeur) {
if (droite == null) return this;
else {
droite = droite.enlever(v);
return this;
}
}
else { // Le noeud courant est à enlever
if (gauche == null) return droite;
else if (droite == null) return gauche;
else {
Nœud_Int succ = droite.noeud_gauche();
succ.droite = droite.enlever_succ();
succ.gauche = gauche;
return succ;
}
}
}
Noeud_Int noeud_gauche() {
// Cette méthode retourne le nœud le plus à gauche;
if (gauche == null) return this;
else return gauche.noeud_gauche();
}
Noeud_Int enlever_succ() {
// Cette méthode enlève le nœud le plus à gauche;
if (gauche == null) return droite;
else {
gauche = gauche.enlever_succ();
return this;
}
}
Le principe d'enlever est le suivant:
Par exemple, soit l'arbre suivant dans lequel le nœud 6 est à enlever:
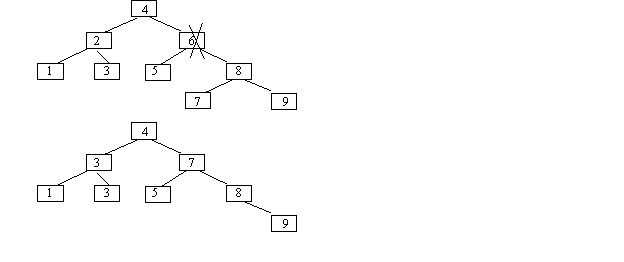
La solution consiste à trouver le nœud contenant la valeur suivante (c'est-à-dire le nœud 7) pour remplacer le 6. Évidemment, il faut ensuite enlever le nœud 7 de sa position initiale. La deuxième figure donne le résultat.
Remarquez qu'avec l'organisation de notre arbre, le nœud qui contient la valeur suivante est le nœud le plus à gauche dans la sous-arbre droite. Ce nœud est trouver par "droite.nœud_gauche()". "enlever_succ()" permet d'enlever ce nœud successeur de sa position initiale.
Remarquez aussi que cette méthode n'est pas optimiser en temps. En effet, il est possible de faire les deux opérations (identification du nœud successeur et le changement de sa position) en même temps.
Finalement, mentionnons un petit problème dans cette réalisation: si la valeur contenue dans succ est répétée dans un autre nœud, l'arbre modifié ne vérifie plus le principe d'organisation (gauche stocke les valeurs <= la valeur de la racine, et droite les valeurs > la valeur de la racine). Imaginons dans le précédent exemple, que le nœud 7 contient plutôt la valeur 8. Dans ce cas, il y aura un nœud 8 à droite d'un nœud 8. Pour remédier à ce problème, il faut plutôt chercher à remplacer le nœud à enlever par le prédécesseur (plutôt que le successeur). Ainsi, même si la valeur du prédécesseur est répétée dans un autre nœud, ce dernier nœud sera à sa gauche dans le nouvel arbre, ce qui ne contredit pas le principe de l'organisation.
Utiliser une classe Arbre différente
Cependant, l'organisation précédente soulève aussi la confusion entre un arbre et un nœud (exactement comme dans le cas de liste). Aussi, il est impossible de manipuler un arbre vide correctement.
Une meilleure façon d'organiser un arbre est de définir une autre classe Arbre comme suit:
class Arbre {
Noeud_Int racine;
<opérations sur l'arbre>
}
Voici maintenant quelques méthodes.
public void ajout(int v) {
// ajouter un nœud contenant la valeur v dans l'arbre;
racine = ajout_dans(racine, v);
}
public Noeud_Int ajout_dans(Noeud_Int n, int v) {
//ajouter dans le sous-arbre dont la racine est n
if (n == null) return new Noeud_Int(v, null, null);
else {
if (v <= n.valeur) gauche = ajout_dans(gauche, v);
else droite = ajout_dans(droite, v);
return n;
}
}
Dans cette version, on est forcé à écrire deux niveaux d'ajout. Le premier niveau ajoute un nœud dans un arbre. Le second niveau utilise la récursivité pour ajouter le nœud à sa position appropriée. On ne peut pas faire une seule méthode qui réalise les deux niveaux, car l'identification "racine" est unique dans un arbre. Elle ne change pas dans la récursion. Ainsi, il est nécessaire d'ajouter un autre paramètre " Nœud_Int n" au deuxième niveau pour que la racine de sous-arbre change dans la récursion.
Mis à part cette différence, le principe de l'opération est le même que précédemment.
public void enlever(int v) {
racine = enlever_dans(racine, v);
}
public Noeud_Int enlever_dans(Noeud_Int n, int v) {
if (v < valeur) {
if (n.gauche == null) return n;
else {
n.gauche = enlever_dans(n.gauche, v);
return n;
}
}
else if (v < valeur) {
if (n.droite == null) return n;
else {
n.droite = enlever_dans(n.droite, v);
return n;
}
}
else { // Le nœud courant est à enlever
if (n.gauche == null) return n.droite;
else if (n.droite == null) return n.gauche;
else {
Noeud_Int succ = noeud_gauche(n.droite);
succ.droite = enlever_succ(n.droite);
succ.gauche = n.gauche;
return succ;
}
}
}
Les méthodes nœud_gauche et enlever_succ sont similaires à la précédente version.
Avec cette séparation entre Arbre et Nœud, il est possible de simplifier l'opération "enlever" en réutilisant la méthode ajout comme suit: quand on a identifié le nœud à enlever, il faut détacher ce nœud (et le sous-arbre) du reste de l'arbre, ensuite, ajouter tous les nœuds qui sont dans les branches gauche et droite de ce nœud à l'arbre. On vous laisse cette méthode comme sujet de réflexion. Cependant, il faut réaliser que cette façon d'enlever un nœud est beaucoup plus coûteuse, car cela nécessite une réorganisation complète des branches sous le nœud à enlever.
Arbre avec une organisation générale
Nous pouvons prendre la même stratégie que pour la liste, de créer une structure très générale, et de définir des opérations sur cette structure générale.
class Node {
Object datum;
int key;
Node left, right;
public Node () {}
public Node (Object d, int k) {
datum = d;
key = k;
left = right = null;
}
public Node (Object d, int k, Node l, Node r) {
datum = d;
key = k;
left = l;
right = r;
}
// méthodes d'accès:
public int getKey() {
return key;
}
public void setKey(int k) {
key = k;
}
public Node getLeft() {
return left;
}
public void setLeft(Node l) {
left = l;
}
...
}
Remarque: Dans cette classe Node, nous avons exigé la variable key en plus de datum. Cela est nécessaire pour pouvoir ordonner les nœuds.
class Tree {
Node root;
<opérations sur l'arbre>
}
Les opérations sur Tree sont très similaires à celle dans la dernière section (Arbre et Nœud_Int). Voici un exemple de ces méthodes.
public void ajout(Object d, int k) {
// ajouter un nœud contenant d dont la clé est k dans l'arbre;
racine = ajout_dans(root, d, k);
}
public Node ajout_dans(Node n, Object d, int k) {
//ajouter un nœud contenant d, dont la clé est k, dans le sous-arbre dont la racine est n;
if (r == null) return new Node (n, k, null, null);
else {
if (k <= n.getKey()) n.setLeft(ajout_dans(n.getLeft(), d, k);
else n.setRight(ajout_dans(n.getRight(), d, k);
return n;
}
}
public void enlever(int k) {
// enlever dans l'arbre le nœud contenant la clé key = k.
racine = enlever_dans(racine, k);
}
public Node enlever_dans(Node n, int k) {
if (k < n.getKey()) {
if (n.getLeft() == null) return n;
else {
n.setLeft(enlever_dans(n.getLeft(), k));
return n;
}
}
else if (k > n.getKey()) {
if (n.getRight() == null) return n;
else {
n.setRight(enlever_dans(n.getRight(), k));
return n;
}
}
else { // Le nœud courant est à enlever
if (n.getLeft() == null) return n.getRight();
else if (n.getRight() == null) return n.getLeft();
else {
Node succ = noeud_gauche(n.getRight());
succ.setRight(enlever_succ(n.getRight()));
succ.setLeft(n.getLeft());
return succ;
}
}
}
Vous pouvez compléter les autres méthodes de la même façon.
Une autre façon générale d'implantation
Dans cette implantation générale, nous avons exigé l'existence de l'attribut "key" en plus de datum. En réalité, la clé est souvent calculée directement à partir de datum. Une autre façon de réaliser les opérations encore plus générales sur un arbre binaire est de poser cette exigence par une interface. Ainsi, nous pouvons déclarer la classe suivante pour un élément que nous pouvons intégrer dans un nœud (à la place de datum dans la précédente version):
interface Elem {
public abstract int key();
}
Pour un nœud d'arbre binaire, nous pouvons établir d'autres contraintes par l'interface suivante:
interface BinNode {
public Object get_element();
public void set_element(Object v);
public BinNode get_gauche();
public void set_gauche(BinNode p);
public BinNode get_droite();
public void set_droite(BinNode p);
}
Cette interface exige seulement l'existence de ces méthodes d'accès.
Maintenant, une classe concrète BinNodePtr qui "implements" cette interface:
class BinNodePtr implements BinNode {
private Object element; // Object relié à ce noeud
private BinNode gauche; // Pointeur à l'enfant gauche
private BinNode droite; // Pointeur à l'enfant droite
<constructeurs>
<méthodes d'accès>
}
Remarquez ici qu'on exige seulement que "element" soit un "Object". Cependant, dans les méthodes de manipulations (plus bas), on fait l'hypothèse que "element" est conforme à l'interface Elem (c'est-à-dire qu'il contient la méthode key()).
Maintenant, la classe pour un arbre binaire de recherche:
class BST { // Binary Search Tree implementation
private BinNode root;
public BST() {
root = null;
}
<méthodes de manipulations d'arbre>
}
Comme exemple, mentionnons seulement la méthode de recherche d'un nœud.
public Elem find(int key) {
return findhelp(root, key);
}
private Elem findhelp(BinNode rt, int key) {
if (rt == null) return null;
Elem it = (Elem)rt.get_element();
if (it.key() > key) return findhelp(rt.get_gauche(), key);
else if (it.key() == key) return it;
else return findhelp(rt.get_droite(), key);
}
Cette méthode est organisée exactement comme précédemment à deux niveaux. Dans le second niveau, il y a un "casting" par l'interface "Elem" - (Elem)rt.get_element(), ce qui veut dire que rt.get_element() doit se conformer à l'interface "Elem". Elem est aussi utilisée comme un type de donnée. En Java, cela est possible: nous pouvons utiliser une interface comme un type de donnée. La contrainte est qu'on ne peut pas faire "new" sur ce type.
Maintenant, quelques mot sur l'utilisation de cette implantation des arbres. Pour pouvoir créer un "element" concret, la classe suivante est définie:
public class IElem implements Elem {
private int value;
...
public int key() { return value; }
...
}
Dans cette classe, notamment, on doit implanter la méthode key().
Vous pouvez examiner plus en détail les programmes disponibles sur le web pour cette version d'implantation:
http://www.iro.umontreal.ca/~nie/IFT1020/Arbre/
Référence additionnelle
Consultez http://www.pads.uwaterloo.ca/Bruno.Preiss/books/opus5/ pour des descriptions additionnelles sur l'arbre binaire.