This page contains some supplementary data for our paper Reconsidering the significance of genomic word frequencies
(written with L. Noé and G. Kucherov).
A preliminary version of the manuscript can be found in
arXiv.
The final version will appear in the journal Trends in Genetics towards the end of 2007.
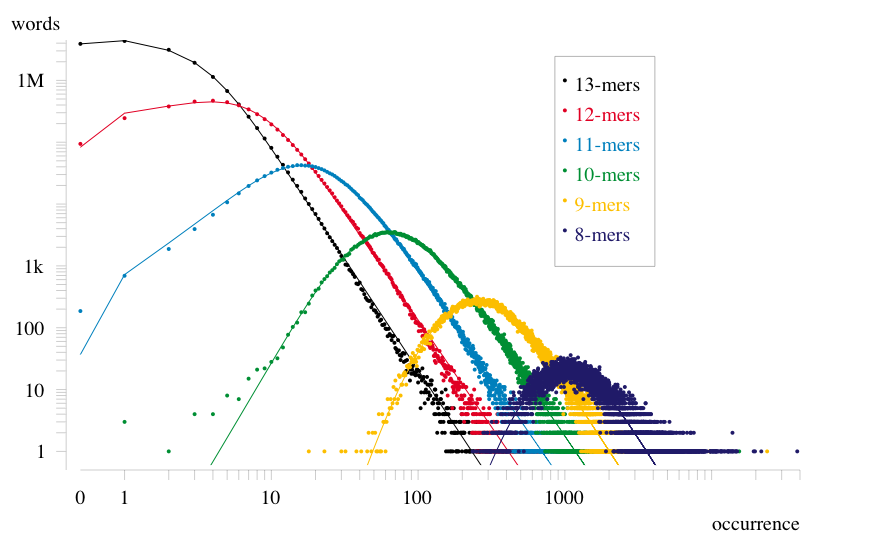 A main finding is that genomic oligonucleotide frequencies follow a
Pareto-lognormal distribution in a wide variety of organisms,
including prokaryotes and eukaryotes. Why? We speculate that
such features are fundamentally attributable to copying processes: genomic
duplications, retrotranscription, tandem repeats and so on.
In other words, global features
of genomic spectra arise from duplicative evolutionary
processes, and not necessarily from intricate word-level
selection on point mutations and deletions that are enacting
adaptation and conservation, or simply obeying structural
constraints.
In practice, the heavy tail of word frequency
distributions means that caution should be exercised when
inferring functionality of motifs from frequency alone,
especially if overrepresentation is related to word
occurrences in random texts.
These random text models include Markov and Bernoulli models,
which are routinely employed in bioinformatics practice to
assess over- and underrepresentation.
Such assessment is often needed in various contexts, including
discovery of sequence motifs
(e.g., transcription factor binding sites) and mobile elements,
homology search (masking repeats and low-complexity regions)
and genome assembly (repeat-masking).
A main finding is that genomic oligonucleotide frequencies follow a
Pareto-lognormal distribution in a wide variety of organisms,
including prokaryotes and eukaryotes. Why? We speculate that
such features are fundamentally attributable to copying processes: genomic
duplications, retrotranscription, tandem repeats and so on.
In other words, global features
of genomic spectra arise from duplicative evolutionary
processes, and not necessarily from intricate word-level
selection on point mutations and deletions that are enacting
adaptation and conservation, or simply obeying structural
constraints.
In practice, the heavy tail of word frequency
distributions means that caution should be exercised when
inferring functionality of motifs from frequency alone,
especially if overrepresentation is related to word
occurrences in random texts.
These random text models include Markov and Bernoulli models,
which are routinely employed in bioinformatics practice to
assess over- and underrepresentation.
Such assessment is often needed in various contexts, including
discovery of sequence motifs
(e.g., transcription factor binding sites) and mobile elements,
homology search (masking repeats and low-complexity regions)
and genome assembly (repeat-masking).
Examples of genomic word frequency distributions
Spectra are computed and fitted to a double Pareto-lognormal distribution for cases when the spectrum spans at least a few hundred frequencies. (By spectrum, we mean the function W(n), where W(n) is the number of words that occur n times in a given genomic sequence.)
Bacteria
- A. aeolicus, 1.59 Mbp (Aquificae)
- B. anthracis, 5.23 Mbp (Firmicutes)
- B. halodurans, 4.2 Mbp (Firmicutes)
- B. japonicum, 9.11 Mbp (Alphaproteobacteria)
- B. longum, 2.26 Mbp (Actinobacteria)
- B. parapertussis, 4.77 Mbp (Betaproteobacteria)
- B. subtilis, 4.21 Mbp (Firmicutes)
- C. jejuni, 1.64 Mbp (Epsilonproteobacteria)
- C. crescentus, 4.02 Mbp (Alphaproteobacteria)
- C. tepidum, 2.15 Mbp (Bacteroidetes/Chlorobi)
- C. trachomatis, 1.04 Mbp (Chlamydiae/Verrucomicrobia)
- C. violaceum, 4.75 Mbp (Betaproteobacteria)
- F. nucleatum, 2.17 Mbp (Fusobacteria)
- G. sulfurreducens, 3.81 Mbp (Deltaproteobacteria)
- H. influenzae, 1.83 Mbp (Gammaproteobacteria)
- L.acidophilus, 1.99 Mbp (Firmicutes)
- M. genitalium, 0.58 Mbp (Firmicutes)
- M. mobile, 0.78 Mbp (Firmicutes)
- M. thermoacetica, 2.63 Mbp (Firmicutes)
- M. pneumoniae, 0.89 Mbp (Firmicutes)
- N. europaea, 2.81 Mbp (Betaproteobacteria)
- N. gonorrhoeae, 2.15 Mbp (Betaproteobacteria)
- O. iheyensis, 3.63 Mbp (Firmicutes)
- P. putida, 6.18 Mbp (Gammaproteobacteria)
- S. elongatus, 2.74 Mbp (Cyanobacteria)
- S. meliloti, 6.69 Mbp (Alphaproteobacteria)
- S. oneidensis, 5.13 Mbp (Gammaproteobacteria)
- S. pyogenes, 1.85 Mbp (Firmicutes)
- T. elongatus, 2.59 Mbp (Cyanobacteria)
- T. maritima, 1.86 Mbp (Thermotogae)
- T. tengcongensis, 2.69 Mbp (Firmicutes)
- T. thermophilus, 2.13 Mbp (Deinococcus-Thermus)
- U. parvum, 0.75 Mbp (Firmicutes)
- V. cholerae, 4.03 Mbp (Gammaproteobacteria)
- W. brevipalpis, 0.7 Mbp (Gammaproteobacteria)
- X. fastidiosa 9a5c, 2.73 Mbp (Gammaproteobacteria)
- X. fastidiosa Temecula1, 2.52 Mbp (Gammaproteobacteria)
- Y. pestis, 4.8 Mbp (Gammaproteobacteria)
Archaea
- A. fulgidus, 2.18 Mbp (Euryarchaeota)
- A. pernix, 1.67 Mbp (Crenarchaeota)
- Halobacterium sp., 2.57 Mbp (Euryarchaeota)
- M. acetivorans, 5.75 Mbp (Euryarchaeota)
- M. jannaschii, 1.74 Mbp (Euryarchaeota)
- M. kandleri, 1.69 Mbp (Euryarchaeota)
- M. maripaludis, 1.66 Mbp (Euryarchaeota)
- M. mazei, 4.1 Mbp (Euryarchaeota)
- M. thermoautotrophicus, 1.75 Mbp (Euryarchaeota)
- N. equitans, 0.49 Mbp (Nanoarchaeota)
- P. abyssi, 1.77 Mbp (Euryarchaeota)
- P. aerophilum, 2.22 Mbp (Crenarchaeota)
- P. furiosus, 1.91 Mbp (Euryarchaeota)
- P. horikoshii, 1.74 Mbp (Euryarchaeota)
- P. torridus, 1.55 Mbp (Euryarchaeota)
- S. solfataricus, 2.99 Mbp (Crenarchaeota)
- S. tokodaii, 2.69 Mbp (Crenarchaeota)
- T. acidophilum, 1.56 Mbp (Euryarchaeota)
Eukaryota
- E. cuniculi, 2.5 Mbp (Fungi)
- E. gossypii, 8.74 Mbp (Fungi - Ascomycetes)
- S. pombe, 12.5 Mbp (Fungi - Ascomycetes)
- C. neoformans, 19.1 Mbp (Fungi - Basidiomycetes)
- D. melanogaster, 120 Mbp
- C. intestinalis chr1, 14.1 Mbp
- D. rerio chr1, 23 Mbp
- G. galllus chr3, 61 Mbp
- A. thaliana, 121 Mbp
Random sequence generators
Random sequences were generated using my
Java executable programs from RandomSequences.jar.
The programs are the following.
ca.umontreal.iro.genome.ShuffleDNASequencefile window_size- Produces a shuffling of the input Fasta sequence in file.
The sequence is partitioned into contiguous pieces with window_size
non-ambiguous (
A,C,G,T) nucleotides. Non-ambiguous nucleotides are garbled within each window by picking a uniform random permutation. ca.umontreal.iro.genome.hash.RandomSequenceSameKmerfile k- Produces a random sequence with the same k-mer distribution and length as the sequence in the Fasta file. In other words, produces a Markov model of order k-1 (if k>1) or a Bernoulli model (if k=1).
ca.umontreal.iro.genome.hash.RandomSequenceCopyPaste[-initlenn] [-gcfraction] [-copym] [-finallenN] [-eventsK]- Produces a random sequence using the copy-and-paste model outlined in the paper.
Initial length and GC content are given by the
initlenandgcswitches (GC fraction should bet between 0 and 1). The initial sequence grows by copying random pieces of length m. Copying stops when the sequence length surpasses N offinallenor after K copy events, whichever happens earlier.
You can launch the programs by using the Java engine you have:
java -cp RandomSequences.jar ca.umontreal.iro.genome....
It may be necessary to allow for larger memory usage:
java -Xmx2000M -cp ...
I very much appreciate if you send me an e-mail in case you decide using my programs.

This software is licensed under the CC-GNU GPL.