|
PLearn 0.1
|
|
PLearn 0.1
|
#include <SparseMatrix.h>
Public Member Functions | |
| int | length () const |
| int | width () const |
| SparseMatrix () | |
| SparseMatrix (int nbrows, int n_columns, int n_non_zero) | |
| SparseMatrix (Vec bRow, Vec eRow, Vec Row, Vec Values, int nbrows) | |
| SparseMatrix (Mat m) | |
| convert Mat into SparseMatrix: | |
| SparseMatrix (string filename) | |
| void | resize (int nbrows, int n_columns, int n_non_zero) |
| void | loadFortran (const char *filename) |
| load SparseMatrix from file in ascii Harwell-Boeing Fortran format: 4-line header, followed by beginRow, row, and values. | |
| void | saveFortran (const char *filename) |
| Mat | toMat () |
| convert to the equivalent full matrix | |
| void | product (const Vec &x, Vec &y) |
| multiply a sparse matrix by a full vector and set resulting vector y = matrix * x | |
| void | diag (Vec &d) |
| extract the diagonal of the sparse matrix: d[i] = A[i,i] | |
| void | diagonalOfSquare (Vec &d) |
| d = diagonal(A'*A), i.e. | |
| real | dotRow (int i, Vec v) |
| return dot product of i-th row with vector v | |
| real | dotColumn (int j, Vec v) |
| return dot product of j-th column with vector v | |
Public Attributes | |
| int | n_rows |
| the dimensions of the matrix are: n_rows x beginRow.length() | |
| Vec | beginRow |
| Vec | endRow |
| Vec | row |
| Vec | values |
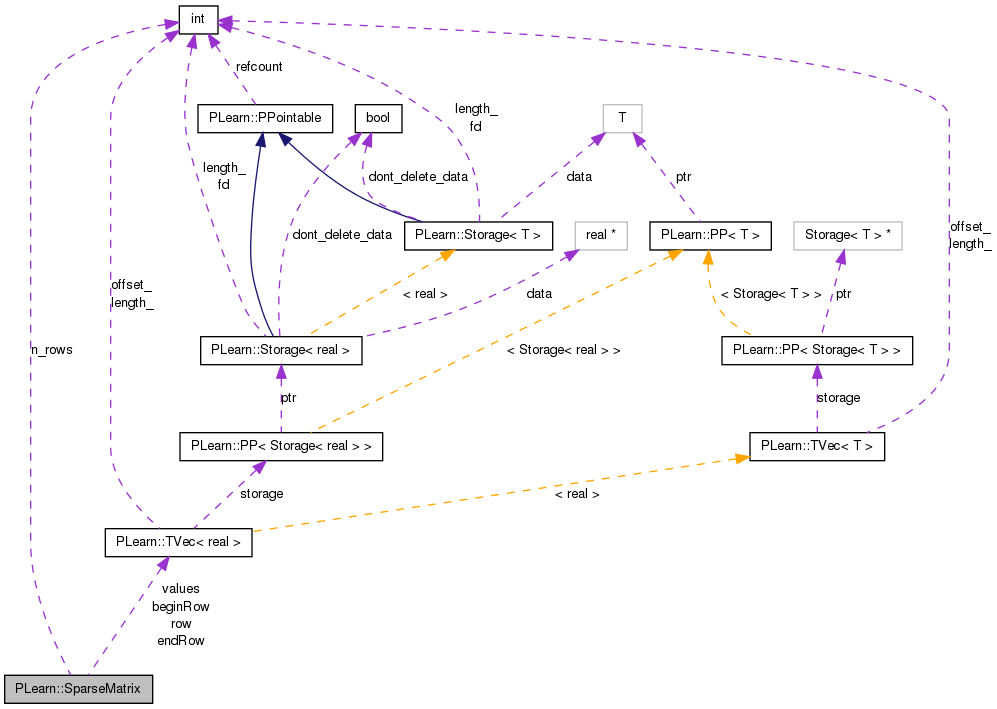
Sparse matrices
beginRow(n_columns): beginning of block of (not necessarily contiguous) elements of column j in the values vector endRow(n_columns): last element of block of (not necessarily contiguous) elements of column j in the values vector row(n_non_zero_elements): row of a non-zero element values(n_non_zero_elements): value of a non-zero element so for example values[k] is the value of an element (i,j) of the matrix such that row[k]=i and beginRow[i]<=k<=endRow[i].
Definition at line 57 of file SparseMatrix.h.
| PLearn::SparseMatrix::SparseMatrix | ( | ) | [inline] |
Definition at line 68 of file SparseMatrix.h.
{}
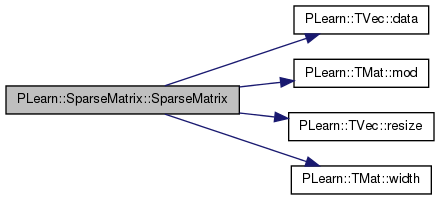
| PLearn::SparseMatrix::SparseMatrix | ( | Mat | m | ) |
convert Mat into SparseMatrix:
Definition at line 149 of file SparseMatrix.cc.
References b, beginRow, PLearn::TVec< T >::data(), endRow, i, j, PLearn::TMat< T >::mod(), n_rows, PLearn::TVec< T >::resize(), row, values, and PLearn::TMat< T >::width().
: n_rows(A.length()), beginRow(A.width()), endRow(A.width()) { int n_nonzero=0; for (int i=0;i<n_rows;i++) { real* Ai=A[i]; for (int j=0;j<A.width();j++) if (Ai[j]!=0) n_nonzero++; } row.resize(n_nonzero); values.resize(n_nonzero); int mod = A.mod(); int k=0; real* v=values.data(); real* r=row.data(); real* b=beginRow.data(); real* e=endRow.data(); for (int j=0;j<A.width();j++) { real* Aij = &A(0,j); b[j] = k; for (int i=0;i<n_rows;i++,Aij+=mod) if (*Aij!=0) { r[k] = i; v[k] = *Aij; k++; } e[j] = k-1; } }
| PLearn::SparseMatrix::SparseMatrix | ( | string | filename | ) | [inline] |
Definition at line 79 of file SparseMatrix.h.
{ loadFortran(filename.c_str()); }
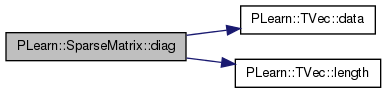
| void PLearn::SparseMatrix::diag | ( | Vec & | d | ) |
extract the diagonal of the sparse matrix: d[i] = A[i,i]
Definition at line 204 of file SparseMatrix.cc.
References beginRow, PLearn::TVec< T >::data(), endRow, j, PLearn::TVec< T >::length(), row, and values.
{
real* d_ = d.data();
real* A_ = values.data();
int k;
for (int j=0;j<beginRow.length();j++)
{
int end=int(endRow[j]);
for (k=(int)beginRow[j];k<=end && int(row[k])!=j;k++);
if (k<=end)
d_[j]=A_[k];
else
d_[j]=0;
}
}
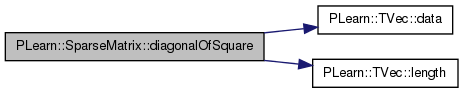
| void PLearn::SparseMatrix::diagonalOfSquare | ( | Vec & | d | ) |
d = diagonal(A'*A), i.e.
d[i] = |A[i]|^2 where A[i] is i-th column
Definition at line 220 of file SparseMatrix.cc.
References beginRow, PLearn::TVec< T >::data(), endRow, j, PLearn::TVec< T >::length(), and values.
{
real* d_ = d.data();
real* A_ = values.data();
int k;
for (int j=0;j<beginRow.length();j++)
{
int end=int(endRow[j]);
real sum2=0;
for (k=(int)beginRow[j];k<=end;k++)
sum2 += A_[k]*A_[k];
d_[j]=sum2;
}
}
return dot product of j-th column with vector v
Definition at line 243 of file SparseMatrix.cc.
References beginRow, PLearn::TVec< T >::data(), endRow, PLearn::TVec< T >::length(), length(), PLERROR, row, and values.
{
#ifdef BOUNDCHECK
if (v.length()!=length())
PLERROR("SparseMatrix::dotColumn(%d,v), v.length_=%d != matrix length=%d",
j,v.length(),length());
#endif
real s=0;
real* v_=v.data();
real* A_=values.data();
for (int k=int(beginRow[j]);k<=int(endRow[j]);k++)
s += A_[k] * v_[int(row[k])];
return s;
}
return dot product of i-th row with vector v
Definition at line 236 of file SparseMatrix.cc.
References PLERROR.
{
PLERROR("SparseMatrix is not appropriate to perform dotRow operations");
return 0;
}
| int PLearn::SparseMatrix::length | ( | ) | const [inline] |
Definition at line 65 of file SparseMatrix.h.
Referenced by dotColumn().
{ return n_rows; }

| void PLearn::SparseMatrix::loadFortran | ( | const char * | filename | ) |
load SparseMatrix from file in ascii Harwell-Boeing Fortran format: 4-line header, followed by beginRow, row, and values.
Definition at line 52 of file SparseMatrix.cc.
{
FILE* fp=fopen(filename,"r");
if (!fp)
PLERROR("SparseMatrix::loadFortran, can't open file %s\n",filename);
int n_cols,n_nonzero;
fscanf(fp,"%*72c%*s%*s%*s%d%d%d%*d",&n_rows, &n_cols, &n_nonzero);
fscanf(fp,"%*s %*s %*s %*s"); // skip some format infos
beginRow.resize(n_cols);
endRow.resize(n_cols);
values.resize(n_nonzero);
row.resize(n_nonzero);
real *brow = beginRow.data();
real *erow = endRow.data();
real *v = values.data();
real *r = row.data();
int i;
for (i = 0; i < n_cols; i++)
{
#ifdef USEFLOAT
fscanf(fp, "%f", &brow[i]);
#endif
#ifdef USEDOUBLE
fscanf(fp, "%lf", &brow[i]);
#endif
brow[i]--;
if (i>0) erow[i-1]=brow[i]-1;
}
erow[n_cols-1]=n_nonzero-1;
fscanf(fp,"%d",&i);
if (i-1!=n_nonzero)
PLERROR("SparseMatrix::loadFortran, inconsistent nnz %d vs %d",
n_nonzero,i);
for (i=0;i<n_nonzero;i++)
{
#ifdef USEFLOAT
fscanf(fp, "%f", &r[i]);
#endif
#ifdef USEDOUBLE
fscanf(fp, "%lf", &r[i]);
#endif
r[i]--;
}
for (i=0;i<n_nonzero;i++)
#ifdef USEFLOAT
fscanf(fp, "%f", &v[i]);
#endif
#ifdef USEDOUBLE
fscanf(fp, "%lf", &v[i]);
#endif
}
multiply a sparse matrix by a full vector and set resulting vector y = matrix * x
Definition at line 182 of file SparseMatrix.cc.
References beginRow, PLearn::TVec< T >::clear(), PLearn::TVec< T >::data(), endRow, i, j, PLearn::TVec< T >::length(), n_rows, PLERROR, row, and values.
{
// y[i] = sum_j A[i,j] x[j]
if (y.length()!=n_rows || x.length()!=beginRow.length())
PLERROR("SparseMatrix(%d,%d)::product(x(%d) -> y(%d)): dimensions don't match",
n_rows,beginRow.length(),x.length(),y.length());
y.clear();
real* y_=y.data();
real* x_=x.data();
real* A_=values.data();
// loop over columns of A, accumulating in y
for (int j=0;j<beginRow.length();j++)
{
real xj = x_[j];
for (int k=(int)beginRow[j];k<=endRow[j];k++)
{
int i=(int)row[k];
y_[i] += A_[k] * xj;
}
}
}
| void PLearn::SparseMatrix::saveFortran | ( | const char * | filename | ) |
Definition at line 105 of file SparseMatrix.cc.
{
FILE* fp=fopen(filename,"w");
if (!fp)
PLERROR("SparseMatrix::saveFortran, can't open file %s\n",filename);
int n_nonzero=values.length(), n_cols = endRow.length();
fprintf(fp,"%72s%8s\n#\nrra %d %d %d 0\n","SparseMatrix ",
filename,
n_rows, n_cols , n_nonzero);
fprintf(fp," (10i8) (10i8) (8f10.3) (8f10.3)\n");
real *brow = beginRow.data();
real *v = values.data();
real *r = row.data();
int i;
for (i = 0; i < n_cols; i++)
//fprintf(fp, "%8d", (int)(brow[i]+1));
fprintf(fp, "%7d ", (int)(brow[i]+1));
fprintf(fp,"%8d\n",values.length()+1);
for (i=0;i<n_nonzero;i++)
fprintf(fp,"%7d ",(int)(r[i]+1));
fprintf(fp,"\n");
for (i=0;i<n_nonzero;i++)
fprintf(fp,"%9f ",v[i]);
fprintf(fp,"\n");
fclose(fp);
}
| Mat PLearn::SparseMatrix::toMat | ( | ) |
convert to the equivalent full matrix
Definition at line 133 of file SparseMatrix.cc.
References c, and PLearn::TMat< T >::length().
{
int n_cols = beginRow.length();
Mat A(n_rows,n_cols);
real* r=row.data();
real* v=values.data();
for (int c=0;c<n_cols;c++)
{
real* Ac = &A(0,c);
int e = (int)endRow[c];
for (int k=(int)beginRow[c];k<=e;k++)
Ac[n_cols*(int)r[k]]=v[k];
}
return A;
}

| int PLearn::SparseMatrix::width | ( | ) | const [inline] |
Definition at line 66 of file SparseMatrix.h.
{ return beginRow.length(); }
Definition at line 60 of file SparseMatrix.h.
Referenced by PLearn::add(), diag(), diagonalOfSquare(), dotColumn(), PLearn::operator+(), product(), PLearn::RowMapSparseMatrix< real >::RowMapSparseMatrix(), and SparseMatrix().
Definition at line 61 of file SparseMatrix.h.
Referenced by PLearn::add(), diag(), diagonalOfSquare(), dotColumn(), PLearn::operator+(), product(), PLearn::RowMapSparseMatrix< real >::RowMapSparseMatrix(), and SparseMatrix().
the dimensions of the matrix are: n_rows x beginRow.length()
Definition at line 59 of file SparseMatrix.h.
Referenced by PLearn::operator+(), product(), and SparseMatrix().
Definition at line 62 of file SparseMatrix.h.
Referenced by PLearn::add(), diag(), dotColumn(), PLearn::operator+(), product(), PLearn::RowMapSparseMatrix< real >::RowMapSparseMatrix(), and SparseMatrix().
Definition at line 63 of file SparseMatrix.h.
Referenced by PLearn::add(), diag(), diagonalOfSquare(), dotColumn(), PLearn::operator+(), product(), PLearn::RowMapSparseMatrix< real >::RowMapSparseMatrix(), and SparseMatrix().
 1.7.4
1.7.4