|
PLearn 0.1
|
|
PLearn 0.1
|
#include <GenMat.h>
Public Member Functions | |
| MatTPlusSumSquaredVec (MatT &A, int alloc_n_vectors) | |
| MatTPlusSumSquaredVec (MatT &A, Mat &X) | |
| void | squaredVecAcc (Vec &x) |
| int | length () const |
| int | width () const |
| void | product (const Vec &x, Vec &y) |
| y = A + sum_t x_t x_t' x | |
| void | diag (Vec &d) |
| void | diagonalOfSquare (Vec &d) |
Public Attributes | |
| MatT & | A_ |
| Mat | X_ |
| the rows of X are the above x_t's | |
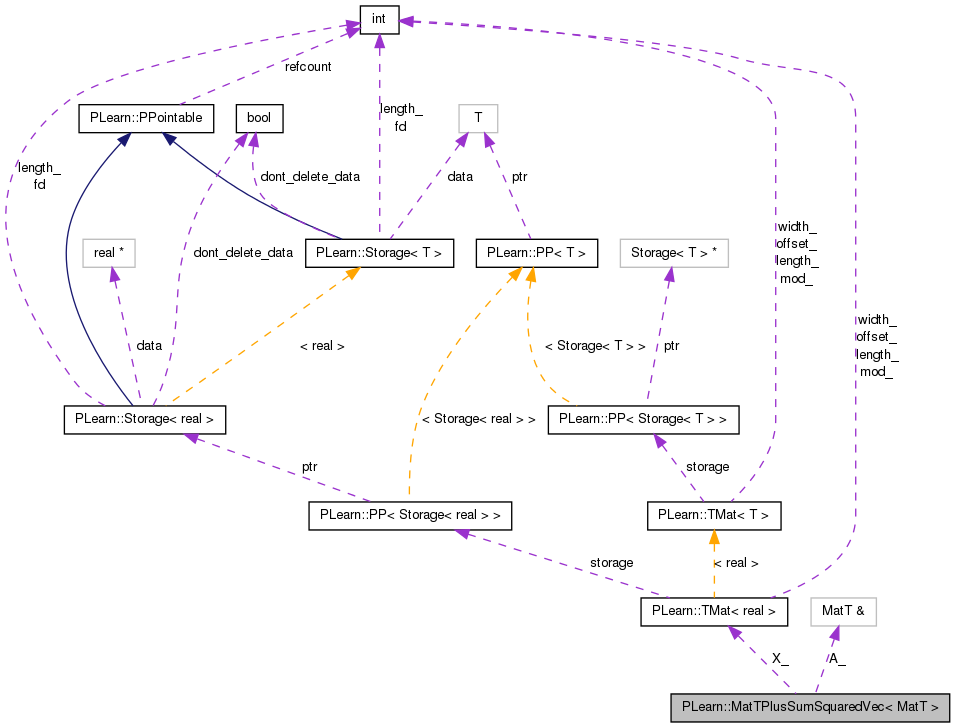
Represents A + sum_{t=1}^T x_t x_t' procedurally keep a generic matrix A and a set of vectors x_t, and performing the matrix vector product with A v + sum_t x_t (x_t . v) The generic matrix A must have the following operations:
void product(const Vec& x, Vec& y); < y = A * x void diagonalOfSquare(Vec& d); < d[i] = |A[i]|^2 where A[i] could either be i-th row or col void diag(Vec& d); < d[i] = A[i,i] int length(); int width();
| PLearn::MatTPlusSumSquaredVec< MatT >::MatTPlusSumSquaredVec | ( | MatT & | A, |
| int | alloc_n_vectors | ||
| ) | [inline] |
| PLearn::MatTPlusSumSquaredVec< MatT >::MatTPlusSumSquaredVec | ( | MatT & | A, |
| Mat & | X | ||
| ) | [inline] |
| void PLearn::MatTPlusSumSquaredVec< MatT >::diag | ( | Vec & | d | ) | [inline] |
| void PLearn::MatTPlusSumSquaredVec< MatT >::diagonalOfSquare | ( | Vec & | d | ) | [inline] |
| int PLearn::MatTPlusSumSquaredVec< MatT >::length | ( | ) | const [inline] |
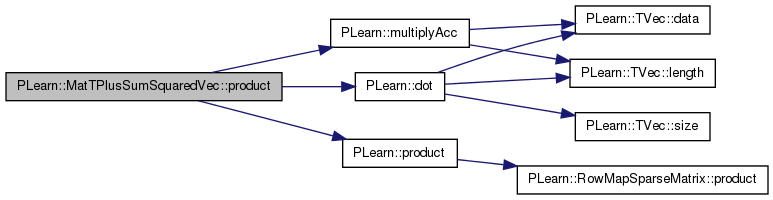
| void PLearn::MatTPlusSumSquaredVec< MatT >::product | ( | const Vec & | x, |
| Vec & | y | ||
| ) | [inline] |
y = A + sum_t x_t x_t' x
Definition at line 178 of file GenMat.h.
References PLearn::dot(), PLearn::multiplyAcc(), and PLearn::product().
{
product(A_, x,y);
for (int t=0;t<X_.length();t++)
{
Vec x_t = X_(t);
multiplyAcc(y, x_t,dot(x_t,x));
}
}
| void PLearn::MatTPlusSumSquaredVec< MatT >::squaredVecAcc | ( | Vec & | x | ) | [inline] |
| int PLearn::MatTPlusSumSquaredVec< MatT >::width | ( | ) | const [inline] |
| MatT& PLearn::MatTPlusSumSquaredVec< MatT >::A_ |
| Mat PLearn::MatTPlusSumSquaredVec< MatT >::X_ |
 1.7.4
1.7.4