|
PLearn 0.1
|
|
PLearn 0.1
|
#include <GaussianDistribution.h>
Public Member Functions | |
| GaussianDistribution () | |
| virtual string | classname () const |
| virtual OptionList & | getOptionList () const |
| virtual OptionMap & | getOptionMap () const |
| virtual RemoteMethodMap & | getRemoteMethodMap () const |
| virtual GaussianDistribution * | deepCopy (CopiesMap &copies) const |
| void | makeDeepCopyFromShallowCopy (CopiesMap &copies) |
| Transform a shallow copy into a deep copy. | |
| virtual void | forget () |
| Resets the distribution. | |
| virtual void | train () |
| The role of the train method is to bring the learner up to stage==nstages, updating the train_stats collector with training costs measured on-line in the process. | |
| virtual void | computeEigenDecomposition () |
| virtual real | log_density (const Vec &x) const |
| Return log of probability density log(p(y | x)). | |
| virtual void | generate (Vec &x) const |
| return a pseudo-random sample generated from the distribution. | |
| virtual int | inputsize () const |
| Overridden so that it does not necessarily need a training set. | |
| virtual void | build () |
| Public build. | |
Static Public Member Functions | |
| static string | _classname_ () |
| static OptionList & | _getOptionList_ () |
| static RemoteMethodMap & | _getRemoteMethodMap_ () |
| static Object * | _new_instance_for_typemap_ () |
| static bool | _isa_ (const Object *o) |
| static void | _static_initialize_ () |
| static const PPath & | declaringFile () |
Public Attributes | |
| Vec | mu |
| Mat | covarmat |
| Vec | eigenvalues |
| Mat | eigenvectors |
| int | k |
| real | gamma |
| real | min_eig |
| bool | use_last_eig |
| float | ignore_weights_below |
| When doing a weighted fitting (weightsize==1), points with a weight below this value will be ignored. | |
| Vec | given_mu |
| Mat | given_covarmat |
Static Public Attributes | |
| static StaticInitializer | _static_initializer_ |
Static Protected Member Functions | |
| static void | declareOptions (OptionList &ol) |
| Declare this class' options. | |
| static void | declareMethods (RemoteMethodMap &rmm) |
| Declare the methods that are remote-callable. | |
Private Types | |
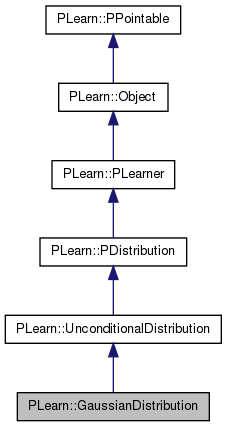
| typedef UnconditionalDistribution | inherited |
Private Member Functions | |
| void | build_ () |
| Internal build. | |
Definition at line 58 of file GaussianDistribution.h.
typedef UnconditionalDistribution PLearn::GaussianDistribution::inherited [private] |
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 60 of file GaussianDistribution.h.
| PLearn::GaussianDistribution::GaussianDistribution | ( | ) |
Definition at line 89 of file GaussianDistribution.cc.
:k(1000), gamma(0), min_eig(0), use_last_eig(false), ignore_weights_below(0) { }
| string PLearn::GaussianDistribution::_classname_ | ( | ) | [static] |
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 74 of file GaussianDistribution.cc.
| OptionList & PLearn::GaussianDistribution::_getOptionList_ | ( | ) | [static] |
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 74 of file GaussianDistribution.cc.
| RemoteMethodMap & PLearn::GaussianDistribution::_getRemoteMethodMap_ | ( | ) | [static] |
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 74 of file GaussianDistribution.cc.
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 74 of file GaussianDistribution.cc.
| Object * PLearn::GaussianDistribution::_new_instance_for_typemap_ | ( | ) | [static] |
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 74 of file GaussianDistribution.cc.
| StaticInitializer GaussianDistribution::_static_initializer_ & PLearn::GaussianDistribution::_static_initialize_ | ( | ) | [static] |
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 74 of file GaussianDistribution.cc.
| void PLearn::GaussianDistribution::build | ( | ) | [virtual] |
Public build.
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 152 of file GaussianDistribution.cc.
References PLearn::UnconditionalDistribution::build(), and build_().
Referenced by PLearn::LocallyMagnifiedDistribution::build_().
{
inherited::build();
build_();
}


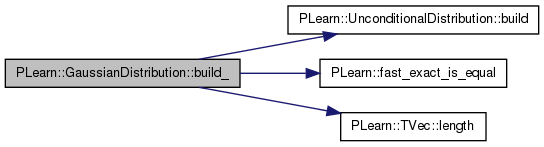
| void PLearn::GaussianDistribution::build_ | ( | ) | [private] |
Internal build.
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 161 of file GaussianDistribution.cc.
References PLearn::UnconditionalDistribution::build(), PLearn::fast_exact_is_equal(), ignore_weights_below, PLearn::TVec< T >::length(), mu, PLERROR, and PLearn::PDistribution::predicted_size.
Referenced by build().
{
if (!fast_exact_is_equal(ignore_weights_below, 0))
PLERROR("In GaussianDistribution::build_ - For the sake of simplicity, the "
"option 'ignore_weights_below' in GaussianDistribution has been "
"removed. If you were using it, please feel free to complain.");
if (mu.length()>0 && predicted_size<=0)
{
predicted_size = mu.length();
inherited::build();
}
}

| string PLearn::GaussianDistribution::classname | ( | ) | const [virtual] |
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 74 of file GaussianDistribution.cc.
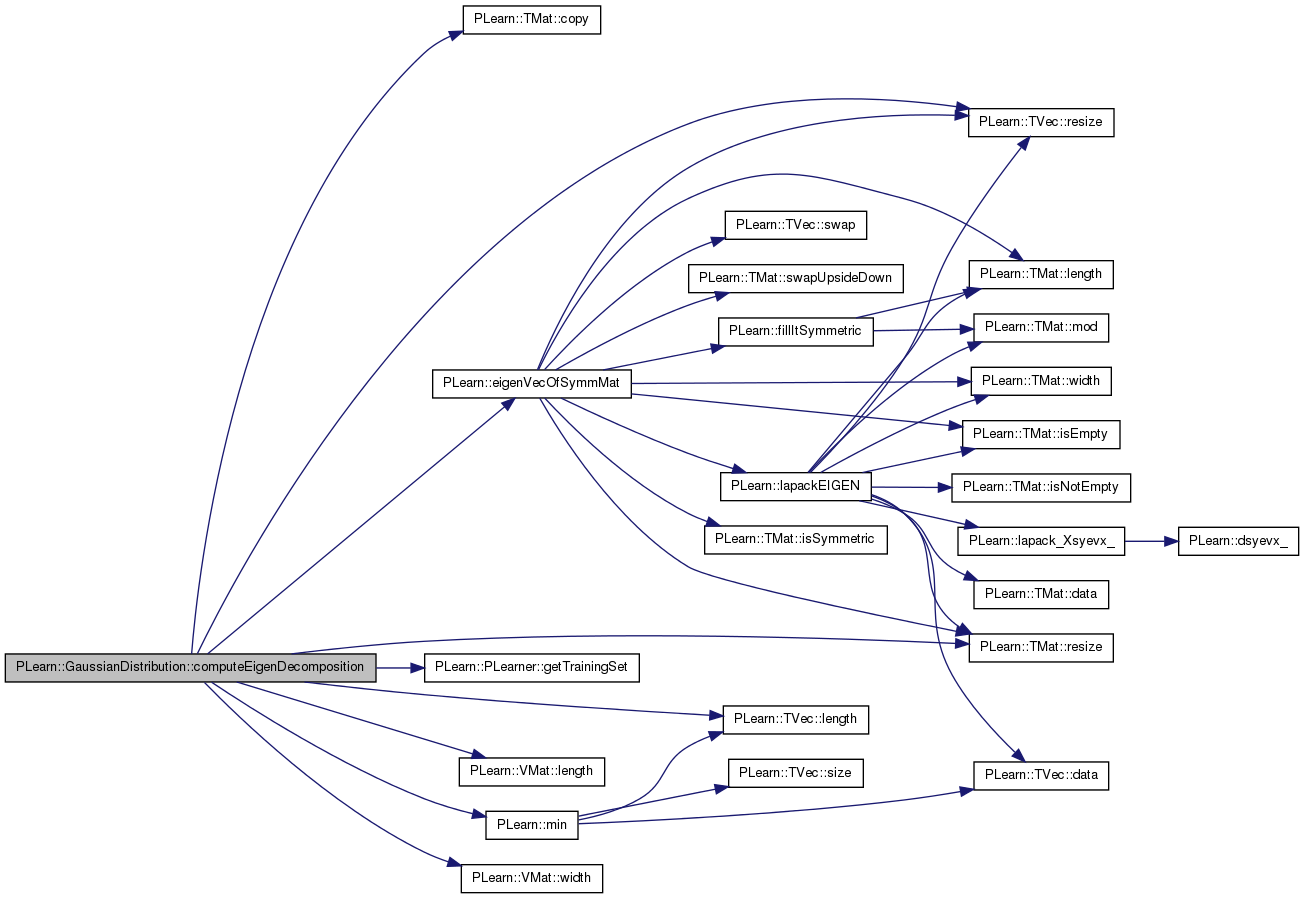
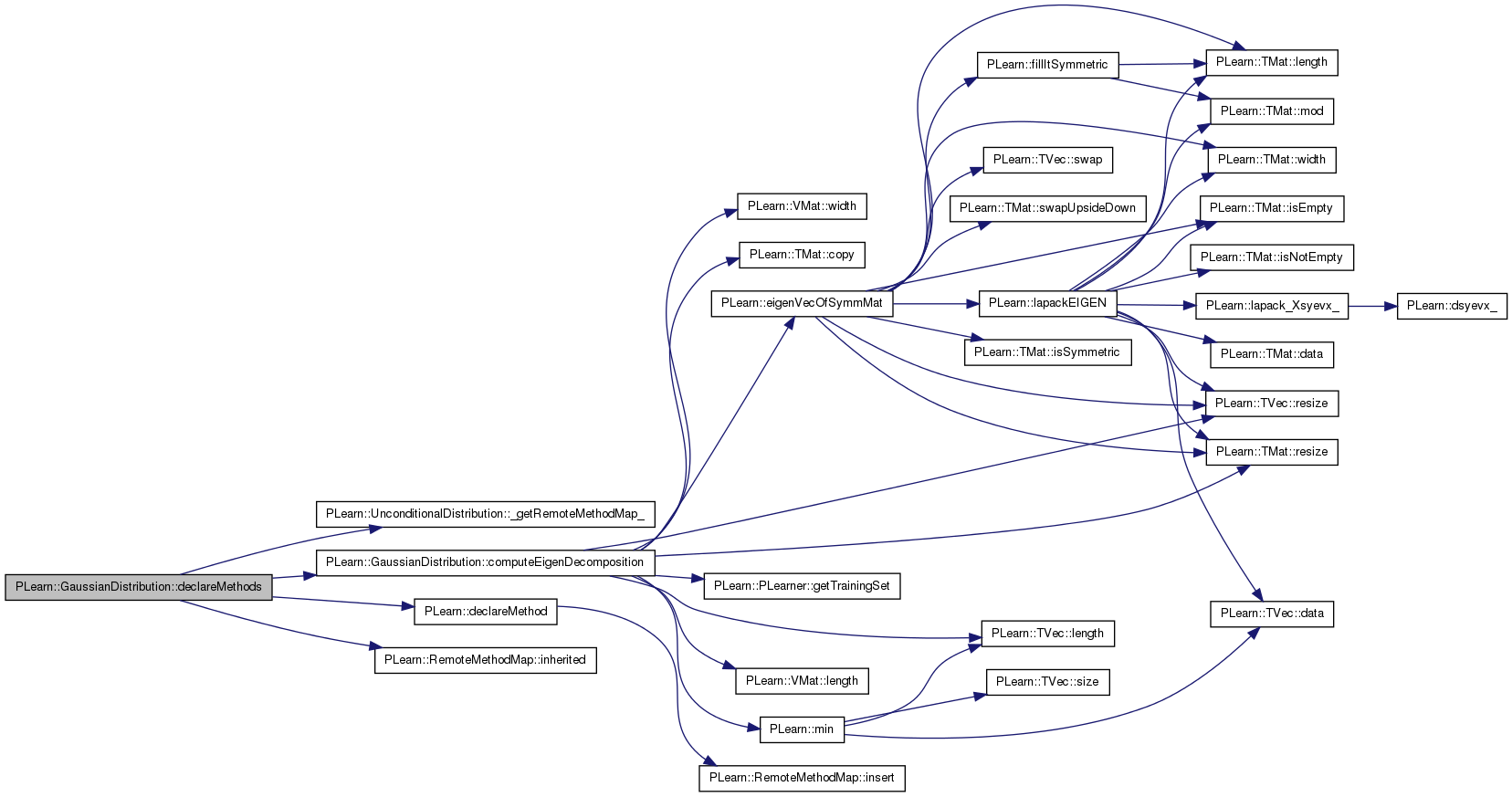
| void PLearn::GaussianDistribution::computeEigenDecomposition | ( | ) | [virtual] |
Definition at line 227 of file GaussianDistribution.cc.
References PLearn::TMat< T >::copy(), covarmat, d, eigenvalues, PLearn::eigenVecOfSymmMat(), eigenvectors, PLearn::PLearner::getTrainingSet(), k, PLearn::TVec< T >::length(), PLearn::VMat::length(), PLearn::min(), mu, PLearn::TMat< T >::resize(), PLearn::TVec< T >::resize(), PLearn::PLearner::verbosity, and PLearn::VMat::width().
Referenced by declareMethods(), and train().
{
VMat training_set = getTrainingSet();
int l = training_set.length();
int d = training_set.width();
int maxneigval = min(k, min(l,d)); // The maximum number of eigenvalues we want.
// Compute eigendecomposition only if there is a training set...
// Otherwise, just empty the eigen-* matrices
static Mat covarmat_tmp;
if (l>0 && maxneigval>0)
{
// On copie covarmat car cette matrice est detruite par la fonction eigenVecOfSymmMat
covarmat_tmp = covarmat.copy();
eigenVecOfSymmMat(covarmat_tmp, maxneigval, eigenvalues, eigenvectors, (verbosity>=4));
int neig = 0;
while(neig<eigenvalues.length() && eigenvalues[neig]>0.)
neig++;
eigenvalues.resize(neig);
eigenvectors.resize(neig,mu.length());
}
else
{
eigenvalues.resize(0);
eigenvectors.resize(0, mu.length());
}
}

| void PLearn::GaussianDistribution::declareMethods | ( | RemoteMethodMap & | rmm | ) | [static, protected] |
Declare the methods that are remote-callable.
Reimplemented from PLearn::PDistribution.
Definition at line 138 of file GaussianDistribution.cc.
References PLearn::UnconditionalDistribution::_getRemoteMethodMap_(), computeEigenDecomposition(), PLearn::declareMethod(), and PLearn::RemoteMethodMap::inherited().
{
// Insert a backpointer to remote methods; note that this is
// different than for declareOptions()
rmm.inherited(inherited::_getRemoteMethodMap_());
declareMethod(
rmm, "computeEigenDecomposition", &GaussianDistribution::computeEigenDecomposition,
(BodyDoc("Compute eigenvectors and corresponding eigenvalues.\n")));
}
| void PLearn::GaussianDistribution::declareOptions | ( | OptionList & | ol | ) | [static, protected] |
Declare this class' options.
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 99 of file GaussianDistribution.cc.
References PLearn::OptionBase::buildoption, covarmat, PLearn::declareOption(), PLearn::UnconditionalDistribution::declareOptions(), eigenvalues, eigenvectors, gamma, given_covarmat, given_mu, ignore_weights_below, k, PLearn::OptionBase::learntoption, min_eig, mu, PLearn::OptionBase::nosave, and use_last_eig.
{
// Build options
declareOption(ol, "k", &GaussianDistribution::k, OptionBase::buildoption,
"number of eigenvectors to keep when training");
declareOption(ol, "gamma", &GaussianDistribution::gamma, OptionBase::buildoption,
"Value to add to the empirical eigenvalues to obtain actual variance.\n");
declareOption(ol, "min_eig", &GaussianDistribution::min_eig, OptionBase::buildoption,
"Imposes a minimum over the actual variances to be used.\n"
"Actual variance used in the principal directions is max(min_eig, eigenvalue_i+gamma)\n");
declareOption(ol, "use_last_eig", &GaussianDistribution::use_last_eig, OptionBase::buildoption,
"If true, the actual variance used for directions in the nullspace of VDV' \n"
"(i.e. orthogonal to the kept eigenvectors) will be the same as the\n"
"actual variance used for the last principal direction. \n"
"If false, the actual variance used for directions in the nullspace \n"
"will be max(min_eig, gamma)\n");
declareOption(ol, "ignore_weights_below", &GaussianDistribution::ignore_weights_below, OptionBase::buildoption | OptionBase::nosave,
"DEPRECATED: When doing a weighted fitting (weightsize==1), points with a weight below this value will be ignored");
declareOption(ol, "given_mu", &GaussianDistribution::given_mu, OptionBase::buildoption,
"If this is set (i.e. not an empty vec), then train will not learn mu from the data, but simply copy its value given here.");
declareOption(ol, "given_covarmat", &GaussianDistribution::given_covarmat, OptionBase::buildoption,
"If this is set (i.e. not an empty mat), then train will not learn covar from the data, but simply copy its value given here.");
// Learnt options
declareOption(ol, "mu", &GaussianDistribution::mu, OptionBase::learntoption, "");
declareOption(ol, "covarmat", &GaussianDistribution::covarmat, OptionBase::learntoption, "");
declareOption(ol, "eigenvalues", &GaussianDistribution::eigenvalues, OptionBase::learntoption, "");
declareOption(ol, "eigenvectors", &GaussianDistribution::eigenvectors, OptionBase::learntoption, "");
inherited::declareOptions(ol);
}

| static const PPath& PLearn::GaussianDistribution::declaringFile | ( | ) | [inline, static] |
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 82 of file GaussianDistribution.h.
:
static void declareOptions(OptionList& ol);
| GaussianDistribution * PLearn::GaussianDistribution::deepCopy | ( | CopiesMap & | copies | ) | const [virtual] |
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 74 of file GaussianDistribution.cc.
| void PLearn::GaussianDistribution::forget | ( | ) | [virtual] |
Resets the distribution.
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 174 of file GaussianDistribution.cc.
{ }
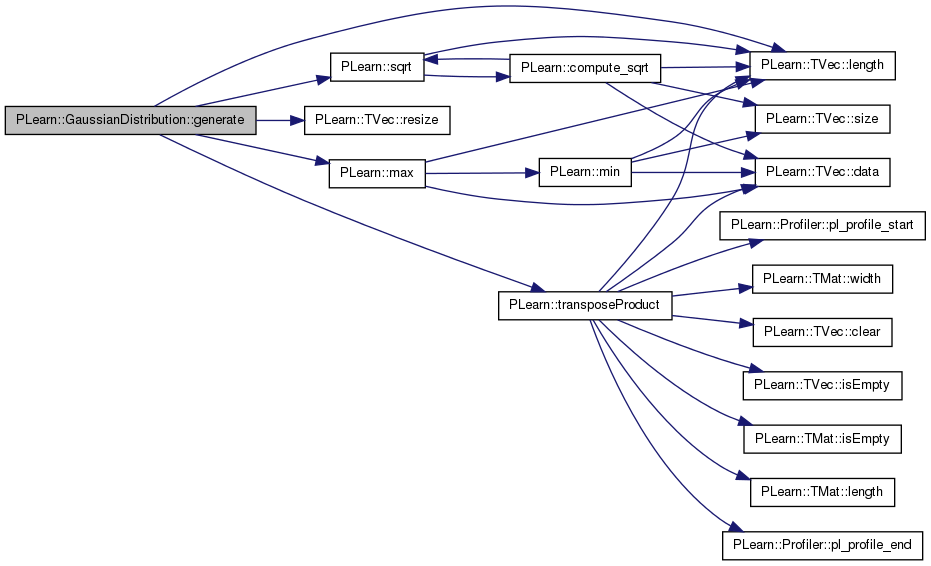
| void PLearn::GaussianDistribution::generate | ( | Vec & | x | ) | const [virtual] |
return a pseudo-random sample generated from the distribution.
Reimplemented from PLearn::PDistribution.
Definition at line 276 of file GaussianDistribution.cc.
References eigenvalues, eigenvectors, gamma, i, PLearn::TVec< T >::length(), m, PLearn::max(), min_eig, mu, PLearn::PLearner::random_gen, PLearn::TVec< T >::resize(), PLearn::sqrt(), PLearn::transposeProduct(), and use_last_eig.
{
static Vec r;
int neig = eigenvalues.length();
int m = mu.length();
r.resize(neig);
real remaining_eig = 0;
if(use_last_eig)
remaining_eig = max(eigenvalues[neig-1]+gamma, min_eig);
else
remaining_eig = max(gamma, min_eig);
random_gen->fill_random_normal(r);
for(int i=0; i<neig; i++)
{
real neweig = max(eigenvalues[i]+gamma, min_eig)-remaining_eig;
r[i] *= sqrt(neweig);
}
x.resize(m);
transposeProduct(x,eigenvectors,r);
if(remaining_eig>0.)
{
r.resize(m);
random_gen->fill_random_normal(r,0,sqrt(remaining_eig));
x += r;
}
x += mu;
}
| OptionList & PLearn::GaussianDistribution::getOptionList | ( | ) | const [virtual] |
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 74 of file GaussianDistribution.cc.
| OptionMap & PLearn::GaussianDistribution::getOptionMap | ( | ) | const [virtual] |
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 74 of file GaussianDistribution.cc.
| RemoteMethodMap & PLearn::GaussianDistribution::getRemoteMethodMap | ( | ) | const [virtual] |
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 74 of file GaussianDistribution.cc.
| int PLearn::GaussianDistribution::inputsize | ( | ) | const [virtual] |
Overridden so that it does not necessarily need a training set.
Reimplemented from PLearn::PLearner.
Definition at line 309 of file GaussianDistribution.cc.
References PLearn::PLearner::inputsize(), PLearn::TVec< T >::length(), mu, and PLearn::PLearner::train_set.
Referenced by train().
{
if (train_set || mu.length() == 0)
return inherited::inputsize();
return mu.length();
}


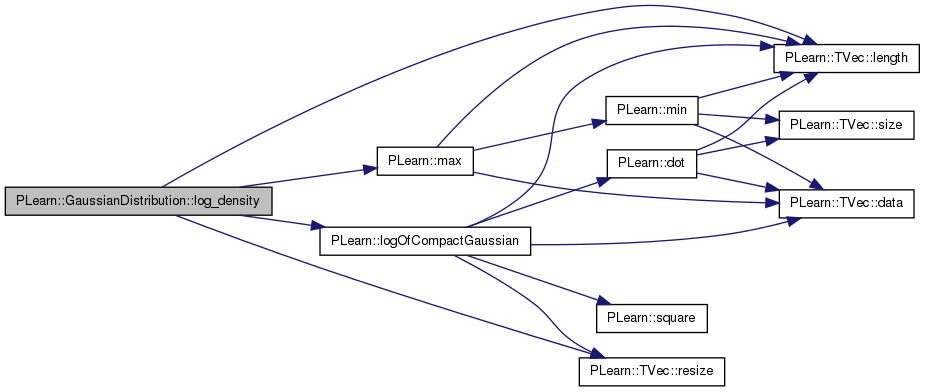
Return log of probability density log(p(y | x)).
Reimplemented from PLearn::PDistribution.
Definition at line 255 of file GaussianDistribution.cc.
References eigenvalues, eigenvectors, gamma, j, PLearn::TVec< T >::length(), PLearn::logOfCompactGaussian(), PLearn::max(), min_eig, mu, PLearn::TVec< T >::resize(), and use_last_eig.
{
static Vec actual_eigenvalues;
if(min_eig<=0 && !use_last_eig)
return logOfCompactGaussian(x, mu, eigenvalues, eigenvectors, gamma, true);
else
{
int neig = eigenvalues.length();
real remaining_eig = 0; // variance for directions in null space
actual_eigenvalues.resize(neig);
for(int j=0; j<neig; j++)
actual_eigenvalues[j] = max(eigenvalues[j]+gamma, min_eig);
if(use_last_eig)
remaining_eig = actual_eigenvalues[neig-1];
else
remaining_eig = max(gamma, min_eig);
return logOfCompactGaussian(x, mu, actual_eigenvalues, eigenvectors, remaining_eig);
}
}
| void PLearn::GaussianDistribution::makeDeepCopyFromShallowCopy | ( | CopiesMap & | copies | ) | [virtual] |
Transform a shallow copy into a deep copy.
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 78 of file GaussianDistribution.cc.
References PLearn::deepCopyField().
{
inherited::makeDeepCopyFromShallowCopy(copies);
deepCopyField(mu, copies);
deepCopyField(covarmat, copies);
deepCopyField(eigenvalues, copies);
deepCopyField(eigenvectors, copies);
deepCopyField(given_mu, copies);
}

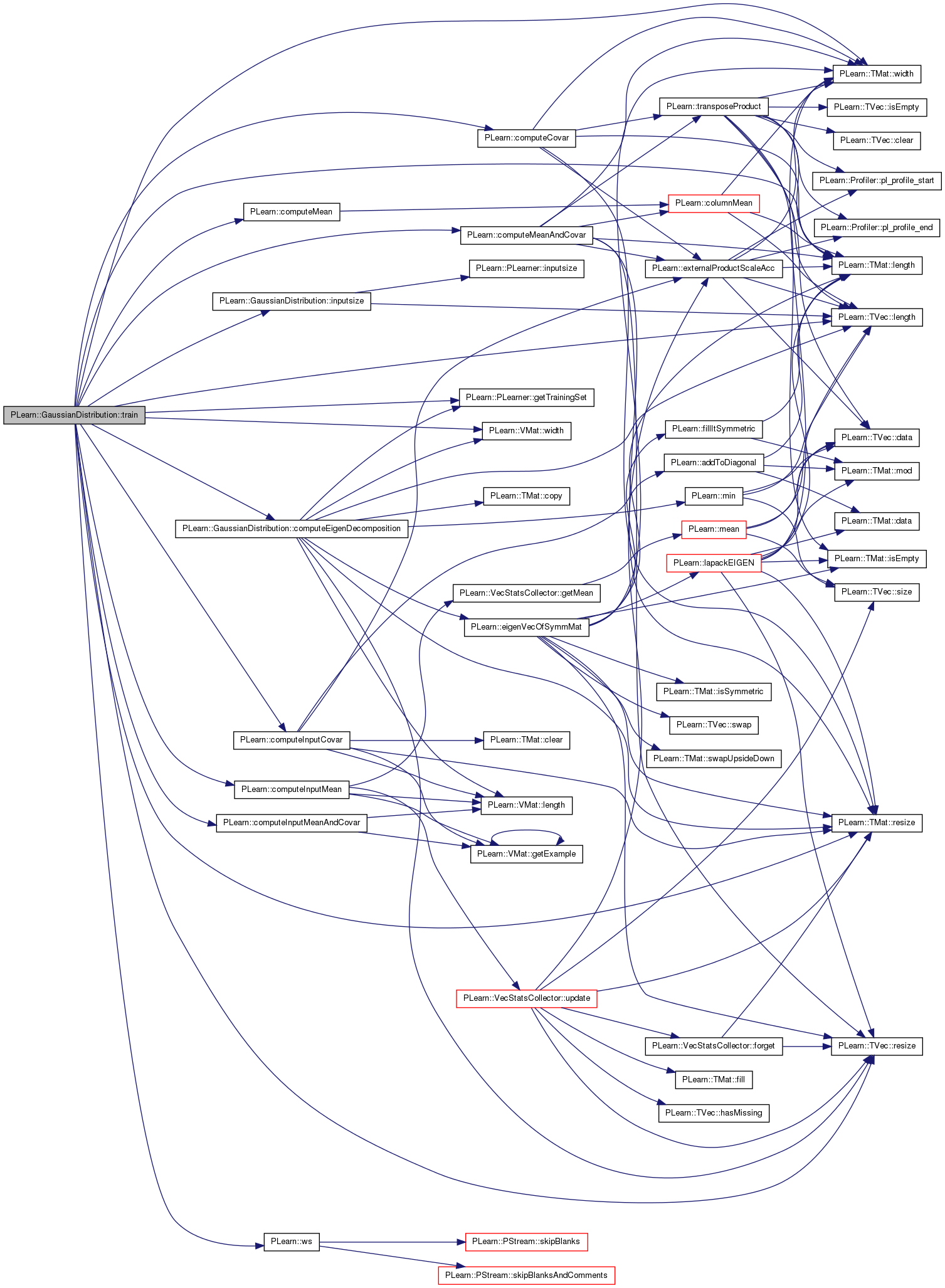
| void PLearn::GaussianDistribution::train | ( | ) | [virtual] |
The role of the train method is to bring the learner up to stage==nstages, updating the train_stats collector with training costs measured on-line in the process.
Reimplemented from PLearn::PDistribution.
Definition at line 177 of file GaussianDistribution.cc.
References PLearn::computeCovar(), computeEigenDecomposition(), PLearn::computeInputCovar(), PLearn::computeInputMean(), PLearn::computeInputMeanAndCovar(), PLearn::computeMean(), PLearn::computeMeanAndCovar(), covarmat, d, PLearn::PLearner::getTrainingSet(), given_covarmat, given_mu, inputsize(), PLearn::TMat< T >::length(), PLearn::TVec< T >::length(), mu, PLASSERT, PLERROR, PLearn::TMat< T >::resize(), PLearn::TVec< T >::resize(), PLearn::TMat< T >::width(), PLearn::VMat::width(), and PLearn::ws().
{
VMat training_set = getTrainingSet();
int d = training_set.width();
int ws = training_set->weightsize();
if(d != inputsize()+ws)
PLERROR("In GaussianDistribution::train width of training_set should be equal to inputsize()+weightsize()");
// First get mean and covariance
if(given_mu.length()>0)
{ // we have a fixed given_mu
PLASSERT(given_covarmat.length()==0);
d = given_mu.length();
mu.resize(d);
mu << given_mu;
if(ws==0)
computeCovar(training_set, mu, covarmat);
else if(ws==1)
computeInputCovar(training_set, mu, covarmat);
else
PLERROR("In GaussianDistribution, weightsize can only be 0 or 1");
}
else if(given_covarmat.length()>0)
{
d=given_covarmat.length();
PLASSERT(d==given_covarmat.width());
covarmat.resize(d,d);
covarmat << given_covarmat;
if(ws==0)
computeMean(training_set, mu);
else if(ws==1)
computeInputMean(training_set, mu);
else
PLERROR("In GaussianDistribution, weightsize can only be 0 or 1");
}
else
{
if(ws==0)
computeMeanAndCovar(training_set, mu, covarmat);
else if(ws==1)
computeInputMeanAndCovar(training_set, mu, covarmat);
else
PLERROR("In GaussianDistribution, weightsize can only be 0 or 1");
}
computeEigenDecomposition();
}
Reimplemented from PLearn::UnconditionalDistribution.
Definition at line 82 of file GaussianDistribution.h.
Definition at line 66 of file GaussianDistribution.h.
Referenced by computeEigenDecomposition(), declareOptions(), and train().
Definition at line 67 of file GaussianDistribution.h.
Referenced by computeEigenDecomposition(), declareOptions(), generate(), and log_density().
Definition at line 68 of file GaussianDistribution.h.
Referenced by computeEigenDecomposition(), declareOptions(), generate(), and log_density().
Definition at line 72 of file GaussianDistribution.h.
Referenced by declareOptions(), generate(), and log_density().
Definition at line 77 of file GaussianDistribution.h.
Referenced by declareOptions(), and train().
Definition at line 76 of file GaussianDistribution.h.
Referenced by declareOptions(), train(), and PLearn::LocallyMagnifiedDistribution::trainLocalDistrAndEvaluateLogDensity().
When doing a weighted fitting (weightsize==1), points with a weight below this value will be ignored.
Definition at line 75 of file GaussianDistribution.h.
Referenced by build_(), PLearn::LocallyMagnifiedDistribution::build_(), and declareOptions().
Definition at line 71 of file GaussianDistribution.h.
Referenced by computeEigenDecomposition(), and declareOptions().
Definition at line 73 of file GaussianDistribution.h.
Referenced by declareOptions(), generate(), and log_density().
Definition at line 65 of file GaussianDistribution.h.
Referenced by build_(), computeEigenDecomposition(), declareOptions(), generate(), inputsize(), log_density(), and train().
Definition at line 74 of file GaussianDistribution.h.
Referenced by declareOptions(), generate(), and log_density().
 1.7.4
1.7.4