|
PLearn 0.1
|
|
PLearn 0.1
|
#include <PCA.h>
Public Member Functions | |
| PCA () | |
| Default constructor. | |
| virtual void | setTrainingSet (VMat training_set, bool call_forget=true) |
| Set nstages to the training_set length under the 'incremental' algo. | |
| virtual void | build () |
| Simply calls inherited::build() then build_() | |
| virtual void | makeDeepCopyFromShallowCopy (CopiesMap &copies) |
| Transforms a shallow copy into a deep copy. | |
| virtual string | classname () const |
| virtual OptionList & | getOptionList () const |
| virtual OptionMap & | getOptionMap () const |
| virtual RemoteMethodMap & | getRemoteMethodMap () const |
| virtual PCA * | deepCopy (CopiesMap &copies) const |
| virtual int | outputsize () const |
| returns the size of this learner's output, (which typically may depend on its inputsize(), targetsize() and set options) | |
| virtual void | forget () |
| (Re-)initializes the PLearner in its fresh state (that state may depend on the 'seed' option) And sets 'stage' back to 0 (this is the stage of a fresh learner!) | |
| virtual void | train () |
| The role of the train method is to bring the learner up to stage==nstages, updating the train_stats collector with training costs measured on-line in the process. | |
| virtual void | computeOutput (const Vec &input, Vec &output) const |
| Computes the output from the input. | |
| void | reconstruct (const Vec &output, Vec &input) const |
| Reconstructs an input from a (possibly partial) output (i.e. the first few princial components kept). | |
| virtual void | computeCostsFromOutputs (const Vec &input, const Vec &output, const Vec &target, Vec &costs) const |
| Computes the costs from already computed output. | |
| virtual TVec< string > | getTestCostNames () const |
| Returns [ "squared_reconstruction_error" ]. | |
| virtual TVec< string > | getTrainCostNames () const |
| No trian costs are computed for this learner. | |
Static Public Member Functions | |
| static string | _classname_ () |
| static OptionList & | _getOptionList_ () |
| static RemoteMethodMap & | _getRemoteMethodMap_ () |
| static Object * | _new_instance_for_typemap_ () |
| static bool | _isa_ (const Object *o) |
| static void | _static_initialize_ () |
| static const PPath & | declaringFile () |
Public Attributes | |
| string | algo |
| The algorithm used to perform the Principal Component Analysis: | |
| int | _horizon |
| Incremental algorithm option: This option specifies a window over which the PCA should be done. | |
| int | ncomponents |
| The number of principal components to keep (that's also the outputsize) | |
| real | sigmasq |
| This gets added to the diagonal of the covariance matrix prior to eigen-decomposition (classical algorithm only) | |
| bool | normalize |
| If true, we divide by sqrt(eigenval) after projecting on the eigenvec. | |
| bool | normalize_warning |
| bool | impute_missing |
| If true, if a missing value is encountered on an input variable for a computeOutput, it is replaced by the estimated mu for that variable before projecting on the principal components. | |
| Vec | mu |
| The (weighted) mean of the samples. | |
| Vec | eigenvals |
| The ncomponents eigenvalues corresponding to the principal directions kept. | |
| Mat | eigenvecs |
| A ncomponents x inputsize matrix containing the principal eigenvectors. | |
Static Public Attributes | |
| static StaticInitializer | _static_initializer_ |
Protected Member Functions | |
| void | classical_algo () |
| void | incremental_algo () |
| void | em_algo () |
| void | em_orth_algo () |
Static Protected Member Functions | |
| static void | declareOptions (OptionList &ol) |
| Declares this class' options. | |
Protected Attributes | |
| VecStatsCollector | _incremental_stats |
| Cache for incremental_algo() | |
| int | _oldest_observation |
| Incremental algo: | |
Private Types | |
| typedef PLearner | inherited |
Private Member Functions | |
| void | build_ () |
| This does the actual building. | |
typedef PLearner PLearn::PCA::inherited [private] |
Reimplemented from PLearn::PLearner.
| PLearn::PCA::PCA | ( | ) |
Default constructor.
Definition at line 53 of file PCA.cc.
: _oldest_observation(-1), algo("classical"), _horizon(-1), ncomponents(2), sigmasq(0), normalize(false), normalize_warning(true), impute_missing(false) { }
| string PLearn::PCA::_classname_ | ( | ) | [static] |
Reimplemented from PLearn::PLearner.
| OptionList & PLearn::PCA::_getOptionList_ | ( | ) | [static] |
Reimplemented from PLearn::PLearner.
| RemoteMethodMap & PLearn::PCA::_getRemoteMethodMap_ | ( | ) | [static] |
Reimplemented from PLearn::PLearner.
Reimplemented from PLearn::PLearner.
| Object * PLearn::PCA::_new_instance_for_typemap_ | ( | ) | [static] |
Reimplemented from PLearn::Object.
| StaticInitializer PCA::_static_initializer_ & PLearn::PCA::_static_initialize_ | ( | ) | [static] |
Reimplemented from PLearn::PLearner.
| void PLearn::PCA::build | ( | ) | [virtual] |
Simply calls inherited::build() then build_()
Reimplemented from PLearn::PLearner.
Definition at line 167 of file PCA.cc.
References PLearn::PLearner::build(), and build_().
Referenced by main().
{
inherited::build();
build_();
}

| void PLearn::PCA::build_ | ( | ) | [private] |
This does the actual building.
Reimplemented from PLearn::PLearner.
Definition at line 176 of file PCA.cc.
References _incremental_stats, algo, PLearn::VecStatsCollector::compute_covariance, PLearn::VecStatsCollector::no_removal_warnings, normalize_warning, and PLWARNING.
Referenced by build().
{
if (normalize_warning)
PLWARNING("In PCA - The default value for option 'normalize' is now 0 instead of 1. Make sure you did not rely on this default value,"
"and set the 'normalize_warning' option to 0 to remove this warning");
if ( algo == "incremental" )
{
_incremental_stats.compute_covariance = true;
_incremental_stats.no_removal_warnings = true;
}
}

| void PLearn::PCA::classical_algo | ( | ) | [protected] |
Definition at line 305 of file PCA.cc.
References PLearn::computeInputMeanAndCovar(), eigenvals, PLearn::eigenVecOfSymmMat(), eigenvecs, PLearn::endl(), PLearn::TMat< T >::hasMissing(), PLearn::TVec< T >::hasMissing(), mu, ncomponents, PLERROR, PLearn::PLearner::report_progress, sigmasq, PLearn::PLearner::stage, and PLearn::PLearner::train_set.
Referenced by train().
{
if ( ncomponents > train_set->inputsize() ) {
ncomponents = train_set->inputsize();
IMP_MODULE_LOG
<< "PCA::train: You asked for " << ncomponents
<< "components, but the training set inputsize is only "
<< train_set->inputsize()
<< "; using " << train_set->inputsize() << " components"
<< endl;
}
PP<ProgressBar> pb;
if (report_progress)
pb = new ProgressBar("Training PCA", 2);
Mat covarmat;
computeInputMeanAndCovar(train_set, mu, covarmat, sigmasq);
if (mu.hasMissing() || covarmat.hasMissing())
PLERROR("PCA::classical_algo: missing values encountered in training set\n");
if (pb)
pb->update(1);
eigenVecOfSymmMat(covarmat, ncomponents, eigenvals, eigenvecs);
if (pb)
pb->update(2);
stage += 1;
}

| string PLearn::PCA::classname | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
| void PLearn::PCA::computeCostsFromOutputs | ( | const Vec & | input, |
| const Vec & | output, | ||
| const Vec & | target, | ||
| Vec & | costs | ||
| ) | const [virtual] |
Computes the costs from already computed output.
The only computed cost is the squared_reconstruction_error
Implements PLearn::PLearner.
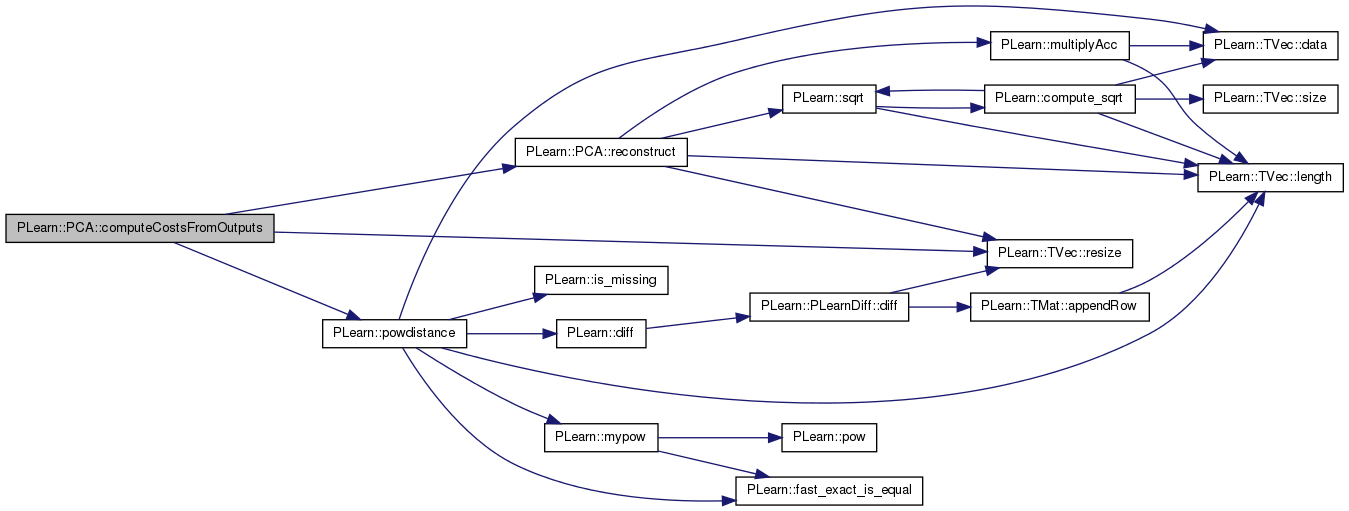
Definition at line 192 of file PCA.cc.
References PLearn::powdistance(), reconstruct(), and PLearn::TVec< T >::resize().
{
static Vec reconstructed_input;
reconstruct(output, reconstructed_input);
costs.resize(1);
costs[0] = powdistance(input, reconstructed_input);
}
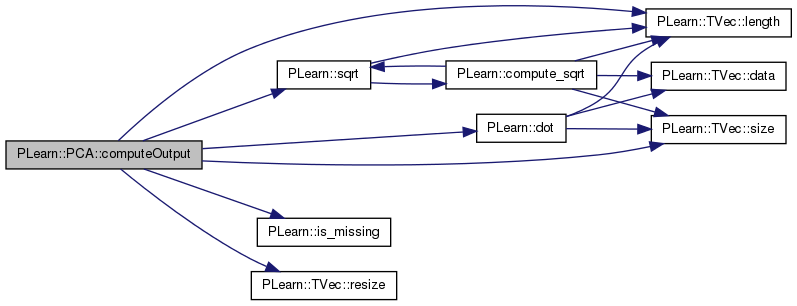
Computes the output from the input.
Reimplemented from PLearn::PLearner.
Definition at line 204 of file PCA.cc.
References PLearn::dot(), eigenvals, eigenvecs, i, impute_missing, PLearn::is_missing(), PLearn::TVec< T >::length(), mu, n, ncomponents, normalize, PLearn::TVec< T >::resize(), PLearn::TVec< T >::size(), PLearn::sqrt(), and x.
{
static Vec x;
x.resize(input.length());
x << input;
// Perform missing-value imputation if requested
if (impute_missing)
for (int i=0, n=x.size() ; i<n ; ++i)
if (is_missing(x[i]))
x[i] = mu[i];
// Project on eigenvectors
x -= mu;
output.resize(ncomponents);
if(normalize)
{
for(int i=0; i<ncomponents; i++)
output[i] = dot(x,eigenvecs(i)) / sqrt(eigenvals[i]);
}
else
{
for(int i=0; i<ncomponents; i++)
output[i] = dot(x,eigenvecs(i));
}
}
| void PLearn::PCA::declareOptions | ( | OptionList & | ol | ) | [static, protected] |
Declares this class' options.
Reimplemented from PLearn::PLearner.
Definition at line 82 of file PCA.cc.
References _horizon, _oldest_observation, algo, PLearn::OptionBase::buildoption, PLearn::declareOption(), PLearn::PLearner::declareOptions(), eigenvals, eigenvecs, impute_missing, PLearn::OptionBase::learntoption, mu, ncomponents, normalize, normalize_warning, and sigmasq.
{
declareOption(
ol, "ncomponents", &PCA::ncomponents, OptionBase::buildoption,
"The number of principal components to keep (that's also the outputsize).");
declareOption(
ol, "sigmasq", &PCA::sigmasq, OptionBase::buildoption,
"This gets added to the diagonal of the covariance matrix prior to\n"
"eigen-decomposition (classical algorighm only)");
declareOption(
ol, "normalize", &PCA::normalize, OptionBase::buildoption,
"If true, we divide by sqrt(eigenval) after projecting on the eigenvec.");
declareOption(
ol, "algo", &PCA::algo, OptionBase::buildoption,
"The algorithm used to perform the Principal Component Analysis:\n"
"- 'classical' : compute the eigenvectors of the covariance matrix\n"
" \n"
"- 'incremental' : Uses the classical algorithm but computes the\n"
" covariance matrix in an incremental manner. When\n"
" 'incremental' is used, a new training set is\n"
" assumed to be a superset of the old training set,\n"
" i.e. begining with the rows of the old training\n"
" set but ending with some new rows.\n"
"\n"
"- 'em' : EM algorithm from \"EM algorithms for PCA and\n"
" SPCA\" by S. Roweis\n"
"\n"
"- 'em_orth' : a variant of 'em', where orthogonal components\n"
" are directly computed\n");
declareOption(
ol, "horizon", &PCA::_horizon, OptionBase::buildoption,
"Incremental algorithm option: This option specifies a window over\n"
"which the PCA should be done. That is, if the length of the training\n"
"set is greater than 'horizon', the observations that will effectively\n"
"contribute to the covariance matrix will only be the last 'horizon'\n"
"ones. All negative values being interpreted as 'keep all observations'.\n"
"\n"
"Default: -1 (all observations are kept)" );
// TODO Option added October 26th, 2004. Should be removed in a few months.
declareOption(
ol, "normalize_warning", &PCA::normalize_warning, OptionBase::buildoption,
"(Temp. option). If true, display a warning about the 'normalize' option.");
declareOption(
ol, "impute_missing", &PCA::impute_missing,
OptionBase::buildoption,
"If true, if a missing value is encountered on an input variable\n"
"for a computeOutput, it is replaced by the estimated mu for that\n"
"variable before projecting on the principal components\n");
// learnt options
declareOption(
ol, "mu", &PCA::mu, OptionBase::learntoption,
"The (weighted) mean of the samples");
declareOption(
ol, "eigenvals", &PCA::eigenvals, OptionBase::learntoption,
"The ncomponents eigenvalues corresponding to the principal directions kept");
declareOption(
ol, "eigenvecs", &PCA::eigenvecs, OptionBase::learntoption,
"A ncomponents x inputsize matrix containing the principal eigenvectors");
// Now call the parent class' declareOptions
inherited::declareOptions(ol);
declareOption(
ol, "oldest_observation", &PCA::_oldest_observation,
OptionBase::learntoption,
"Incremental algo:\n"
"The first time values are fed to _incremental_stats, we must remember\n"
"the first observation in order not to remove observation that never\n"
"contributed to the covariance matrix.\n"
"\n"
"Initialized to -1;" );
}

| static const PPath& PLearn::PCA::declaringFile | ( | ) | [inline, static] |
Reimplemented from PLearn::PLearner.
Reimplemented from PLearn::PLearner.
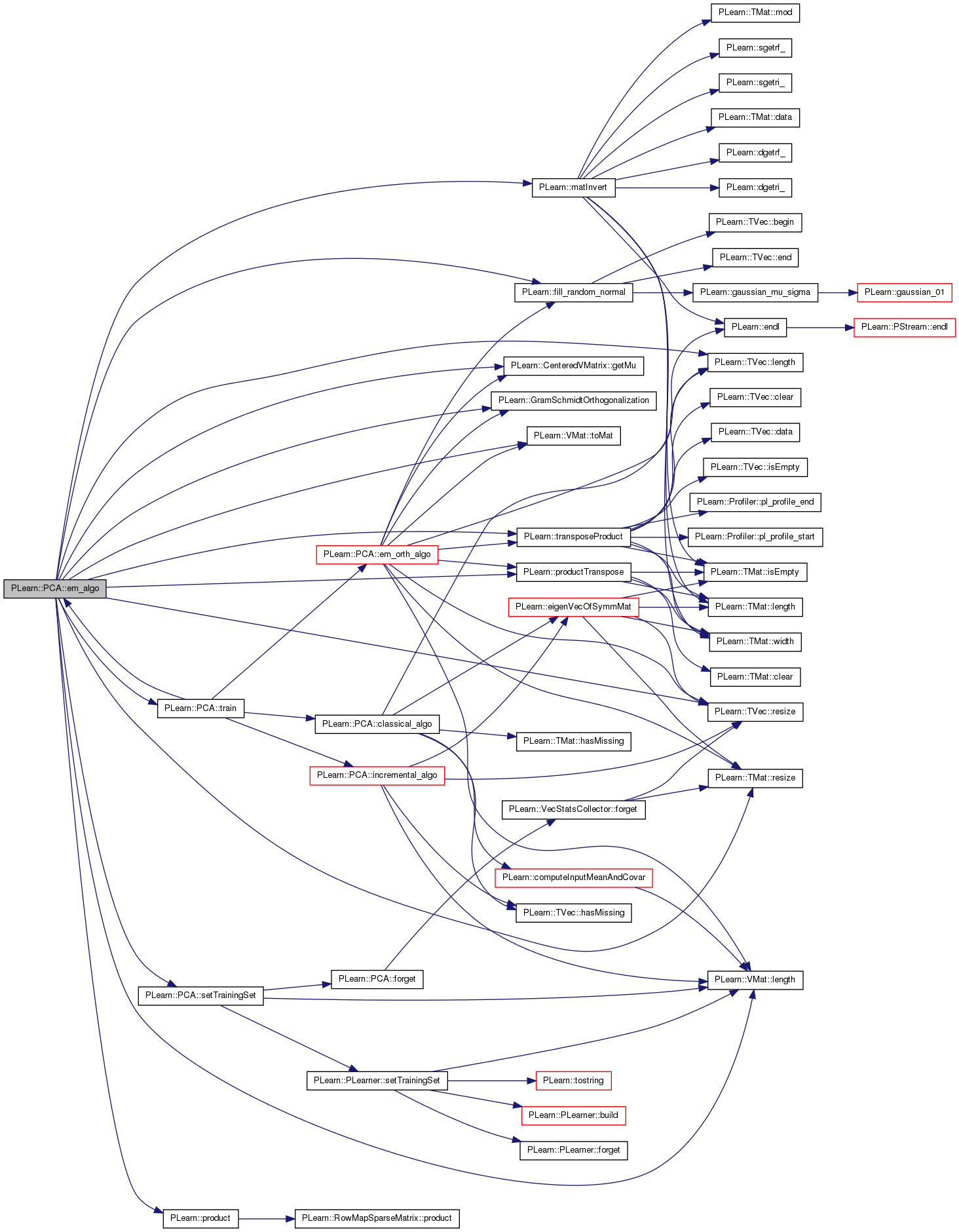
| void PLearn::PCA::em_algo | ( | ) | [protected] |
Definition at line 407 of file PCA.cc.
References eigenvals, eigenvecs, PLearn::fill_random_normal(), PLearn::CenteredVMatrix::getMu(), PLearn::GramSchmidtOrthogonalization(), PLearn::TVec< T >::length(), PLearn::VMat::length(), PLearn::matInvert(), mu, n, ncomponents, normalize, PLearn::PLearner::nstages, PLWARNING, PLearn::product(), PLearn::productTranspose(), PLearn::PLearner::report_progress, PLearn::TMat< T >::resize(), PLearn::TVec< T >::resize(), setTrainingSet(), PLearn::PLearner::stage, PLearn::VMat::toMat(), train(), PLearn::PLearner::train_set, and PLearn::transposeProduct().
Referenced by train().
{
PP<ProgressBar> pb;
int n = train_set->length();
int p = train_set->inputsize();
int k = ncomponents;
// Fill the matrix C with random data.
Mat C(k,p);
fill_random_normal(C);
// Center the data.
VMat centered_data = new CenteredVMatrix(new GetInputVMatrix(train_set));
Vec sample_mean = static_cast<CenteredVMatrix*>((VMatrix*) centered_data)->getMu();
mu.resize(sample_mean.length());
mu << sample_mean;
Mat Y = centered_data.toMat();
Mat X(n,k);
Mat tmp_k_k(k,k);
Mat tmp_k_k_2(k,k);
Mat tmp_p_k(p,k);
Mat tmp_k_n(k,n);
// Iterate through EM.
if (report_progress)
pb = new ProgressBar("Training EM PCA", nstages - stage);
int init_stage = stage;
while (stage < nstages) {
// E-step: X <- Y C' (C C')^-1
productTranspose(tmp_k_k, C, C);
matInvert(tmp_k_k, tmp_k_k_2);
transposeProduct(tmp_p_k, C, tmp_k_k_2);
product(X, Y, tmp_p_k);
// M-step: C <- (X' X)^-1 X' Y
transposeProduct(tmp_k_k, X, X);
matInvert(tmp_k_k, tmp_k_k_2);
productTranspose(tmp_k_n, tmp_k_k_2, X);
product(C, tmp_k_n, Y);
stage++;
if (report_progress)
pb->update(stage - init_stage);
}
// Compute the orthonormal projection matrix.
int n_base = GramSchmidtOrthogonalization(C);
if (n_base != k) {
PLWARNING("In PCA::train - The rows of C are not linearly independent");
}
// Compute the projected data.
productTranspose(X, Y, C);
// And do a PCA to get the eigenvectors and eigenvalues.
PCA true_pca;
VMat proj_data(X);
true_pca.ncomponents = k;
true_pca.normalize = 0;
true_pca.setTrainingSet(proj_data);
true_pca.train();
// Transform back eigenvectors to input space.
eigenvecs.resize(k, p);
product(eigenvecs, true_pca.eigenvecs, C);
eigenvals.resize(k);
eigenvals << true_pca.eigenvals;
}

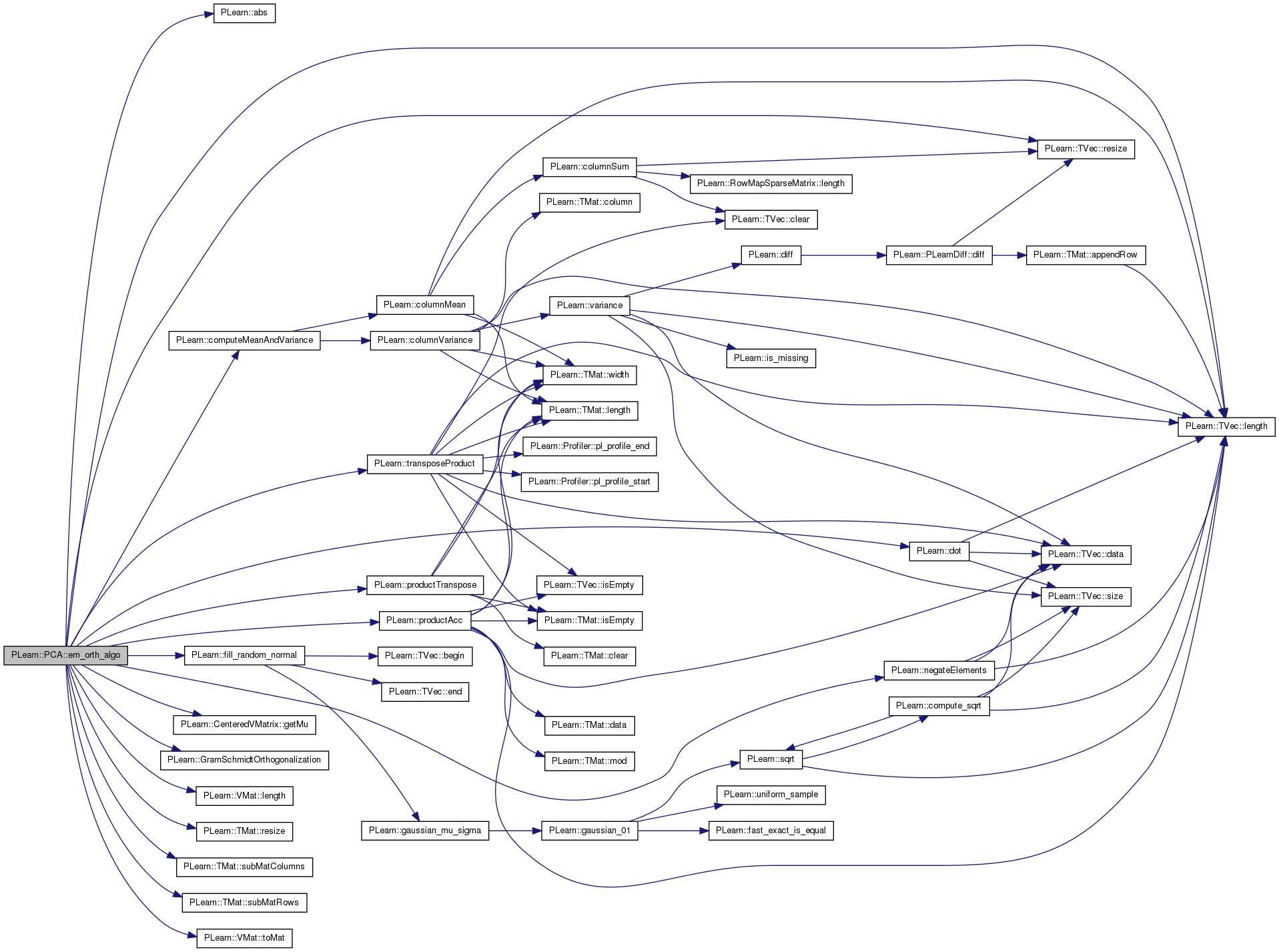
| void PLearn::PCA::em_orth_algo | ( | ) | [protected] |
Definition at line 473 of file PCA.cc.
References PLearn::abs(), PLearn::computeMeanAndVariance(), PLearn::dot(), eigenvals, eigenvecs, PLearn::fill_random_normal(), PLearn::CenteredVMatrix::getMu(), PLearn::GramSchmidtOrthogonalization(), i, j, PLearn::TVec< T >::length(), PLearn::VMat::length(), mu, n, ncomponents, PLearn::negateElements(), normalize, PLearn::PLearner::nstages, PLWARNING, PLearn::productAcc(), PLearn::productTranspose(), PLearn::PLearner::report_progress, PLearn::TMat< T >::resize(), PLearn::TVec< T >::resize(), PLearn::PLearner::stage, PLearn::TMat< T >::subMatColumns(), PLearn::TMat< T >::subMatRows(), PLearn::VMat::toMat(), PLearn::PLearner::train_set, and PLearn::transposeProduct().
Referenced by train().
{
PP<ProgressBar> pb;
int n = train_set->length();
int p = train_set->inputsize();
int k = ncomponents;
// Fill the matrix C with random data.
Mat C(k,p);
fill_random_normal(C);
// Ensure it is orthonormal.
GramSchmidtOrthogonalization(C);
// Center the data.
VMat centered_data = new CenteredVMatrix(new GetInputVMatrix(train_set));
Vec sample_mean = static_cast<CenteredVMatrix*>((VMatrix*) centered_data)->getMu();
mu.resize(sample_mean.length());
mu << sample_mean;
Mat Y = centered_data.toMat();
Mat Y_copy(n,p);
Mat X(n,k);
Mat tmp_k_k(k,k);
Mat tmp_k_k_2(k,k);
Mat tmp_p_k(p,k);
Mat tmp_k_n(k,n);
Mat tmp_n_1(n,1);
Mat tmp_n_p(n,p);
Mat X_j, C_j;
Mat x_j_prime_x_j(1,1);
// Iterate through EM.
if (report_progress)
pb = new ProgressBar("Training EM PCA", nstages - stage);
int init_stage = stage;
Y_copy << Y;
while (stage < nstages) {
Y << Y_copy;
for (int j = 0; j < k; j++) {
C_j = C.subMatRows(j, 1);
X_j = X.subMatColumns(j,1);
// E-step: X_j <- Y C_j'
productTranspose(X_j, Y, C_j);
// M-step: C_j <- (X_j' X_j)^-1 X_j' Y
transposeProduct(x_j_prime_x_j, X_j, X_j);
transposeProduct(C_j, X_j, Y);
C_j /= x_j_prime_x_j(0,0);
// Normalize the new direction.
PLearn::normalize(C_j, 2.0);
// Subtract the component along this new direction, so as to
// obtain orthogonal directions.
productTranspose(tmp_n_1, Y, C_j);
negateElements(Y);
productAcc(Y, tmp_n_1, C_j);
negateElements(Y);
}
stage++;
if (report_progress)
pb->update(stage - init_stage);
}
// Check orthonormality of C.
for (int i = 0; i < k; i++) {
for (int j = i; j < k; j++) {
real dot_i_j = dot(C(i), C(j));
if (i != j) {
if (abs(dot_i_j) > 1e-6) {
PLWARNING("In PCA::train - It looks like some vectors are not orthogonal");
}
} else {
if (abs(dot_i_j - 1) > 1e-6) {
PLWARNING("In PCA::train - It looks like a vector is not normalized");
}
}
}
}
// Compute the projected data.
Y << Y_copy;
productTranspose(X, Y, C);
// Compute the empirical variance on each projected axis, in order
// to obtain the eigenvalues.
VMat X_vm(X);
Vec mean_proj, var_proj;
computeMeanAndVariance(X_vm, mean_proj, var_proj);
eigenvals.resize(k);
eigenvals << var_proj;
// Copy the eigenvectors.
eigenvecs.resize(k, p);
eigenvecs << C;
}

| void PLearn::PCA::forget | ( | ) | [virtual] |
(Re-)initializes the PLearner in its fresh state (that state may depend on the 'seed' option) And sets 'stage' back to 0 (this is the stage of a fresh learner!)
Reimplemented from PLearn::PLearner.
Definition at line 254 of file PCA.cc.
References _incremental_stats, _oldest_observation, algo, PLearn::VecStatsCollector::forget(), and PLearn::PLearner::stage.
Referenced by setTrainingSet().
{
stage = 0;
if ( algo == "incremental" )
{
_incremental_stats.forget();
_oldest_observation = -1;
}
}


| OptionList & PLearn::PCA::getOptionList | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
| OptionMap & PLearn::PCA::getOptionMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
| RemoteMethodMap & PLearn::PCA::getRemoteMethodMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
| TVec< string > PLearn::PCA::getTestCostNames | ( | ) | const [virtual] |
Returns [ "squared_reconstruction_error" ].
Implements PLearn::PLearner.
Definition at line 268 of file PCA.cc.
{
return TVec<string>(1,"squared_reconstruction_error");
}
| TVec< string > PLearn::PCA::getTrainCostNames | ( | ) | const [virtual] |
No trian costs are computed for this learner.
Implements PLearn::PLearner.
Definition at line 276 of file PCA.cc.
{
return TVec<string>();
}
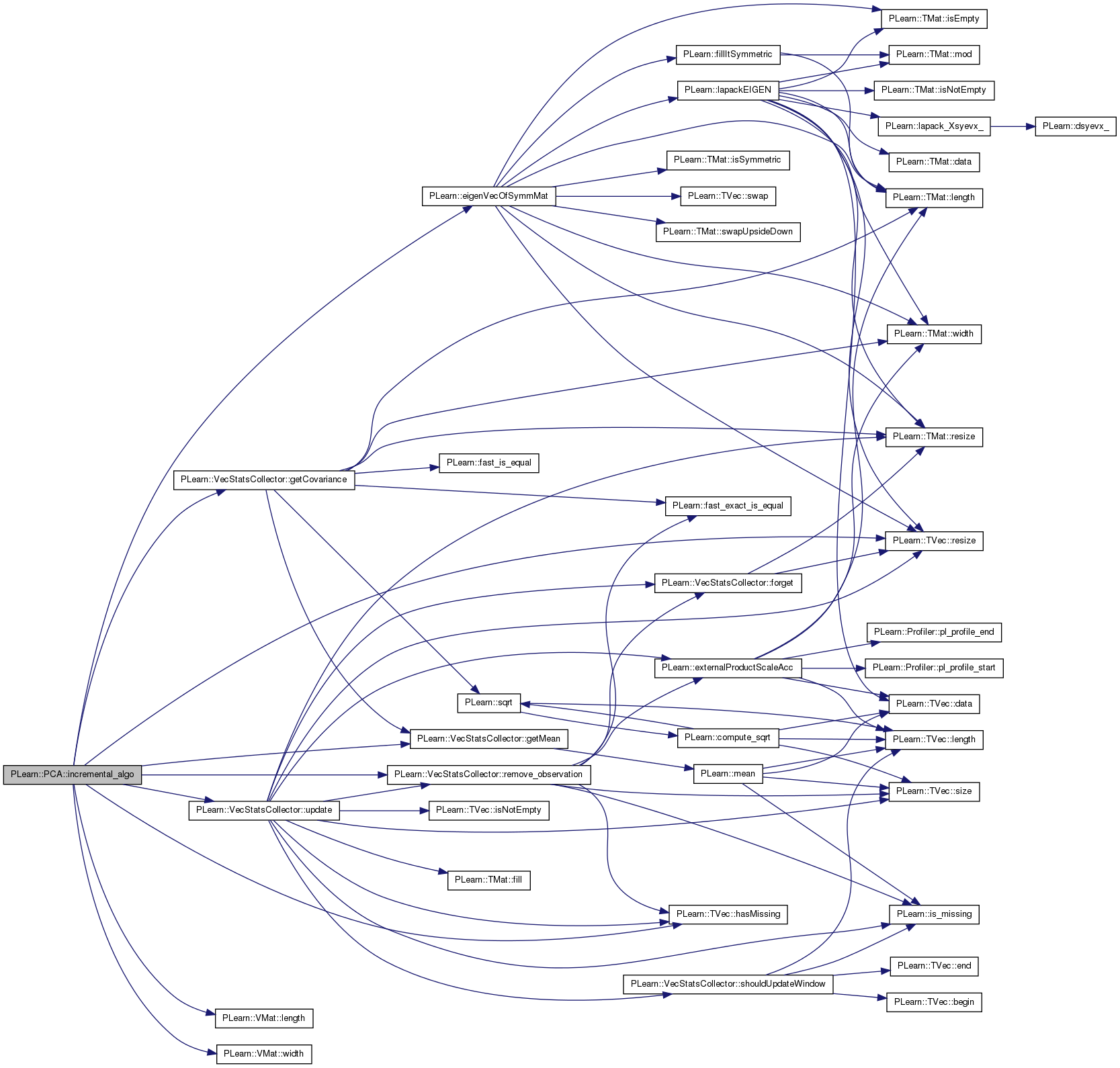
| void PLearn::PCA::incremental_algo | ( | ) | [protected] |
On the first call, there is no need to manage data prior to the window, if any.
Definition at line 335 of file PCA.cc.
References _horizon, _incremental_stats, _oldest_observation, eigenvals, PLearn::eigenVecOfSymmMat(), eigenvecs, PLearn::VecStatsCollector::getCovariance(), PLearn::VecStatsCollector::getMean(), PLearn::TVec< T >::hasMissing(), PLearn::VMat::length(), mu, ncomponents, PLASSERT, PLERROR, PLearn::VecStatsCollector::remove_observation(), PLearn::PLearner::report_progress, PLearn::TVec< T >::resize(), PLearn::PLearner::stage, PLearn::PLearner::train_set, PLearn::VecStatsCollector::update(), and PLearn::VMat::width().
Referenced by train().
{
PP<ProgressBar> pb;
if (report_progress)
pb = new ProgressBar("Incremental PCA", 2);
int start = stage;
if ( stage == 0 && _horizon > 0 )
{
int window_start = train_set.length() - _horizon;
start = window_start > 0 ? window_start : 0;
}
/*
The first time values are fed to _incremental_stats, we must remember
the first observation in order not to remove observation that never
contributed to the covariance matrix.
See the following 'if ( old >= oldest_observation )' statement.
*/
if ( _oldest_observation == -1 )
_oldest_observation = start;
PLASSERT( _horizon <= 0 || (start-_horizon) <= _oldest_observation );
Vec observation;
for ( int obs=start; obs < train_set.length(); obs++ )
{
observation.resize( train_set.width() );
// Stores the new observation
observation << train_set( obs );
if (observation.hasMissing())
PLERROR("PCA::incremental_algo: missing values encountered in training set\n");
// This adds the contribution of the new observation
_incremental_stats.update( observation );
if ( _horizon > 0 &&
(obs - _horizon) == _oldest_observation )
{
// Stores the old observation
observation << train_set( _oldest_observation );
// This removes the contribution of the old observation
_incremental_stats.remove_observation( observation );
_oldest_observation++;
}
}
if (pb)
pb->update(1);
// Recomputes the eigenvals and eigenvecs from the updated
// incremental statistics
mu = _incremental_stats.getMean();
Mat covarmat = _incremental_stats.getCovariance();
eigenVecOfSymmMat( covarmat, ncomponents, eigenvals, eigenvecs );
if (pb)
pb->update(2);
// Remember the number of observation
stage = train_set.length();
}

| void PLearn::PCA::makeDeepCopyFromShallowCopy | ( | CopiesMap & | copies | ) | [virtual] |
Transforms a shallow copy into a deep copy.
Reimplemented from PLearn::PLearner.
Definition at line 284 of file PCA.cc.
References PLearn::deepCopyField(), eigenvals, eigenvecs, PLearn::PLearner::makeDeepCopyFromShallowCopy(), and mu.
{
inherited::makeDeepCopyFromShallowCopy(copies);
deepCopyField(mu, copies);
deepCopyField(eigenvals, copies);
deepCopyField(eigenvecs, copies);
}

| int PLearn::PCA::outputsize | ( | ) | const [virtual] |
returns the size of this learner's output, (which typically may depend on its inputsize(), targetsize() and set options)
Implements PLearn::PLearner.
Definition at line 296 of file PCA.cc.
References ncomponents.
{
return ncomponents;
}
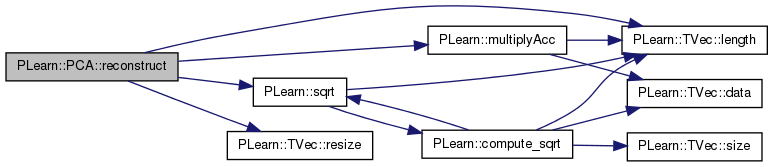
Reconstructs an input from a (possibly partial) output (i.e. the first few princial components kept).
Definition at line 588 of file PCA.cc.
References eigenvals, eigenvecs, i, PLearn::TVec< T >::length(), mu, PLearn::multiplyAcc(), n, normalize, PLearn::TVec< T >::resize(), and PLearn::sqrt().
Referenced by computeCostsFromOutputs().
{
input.resize(mu.length());
input << mu;
int n = output.length();
if(normalize)
{
for(int i=0; i<n; i++)
multiplyAcc(input, eigenvecs(i), output[i]*sqrt(eigenvals[i]));
}
else
{
for(int i=0; i<n; i++)
multiplyAcc(input, eigenvecs(i), output[i]);
}
}

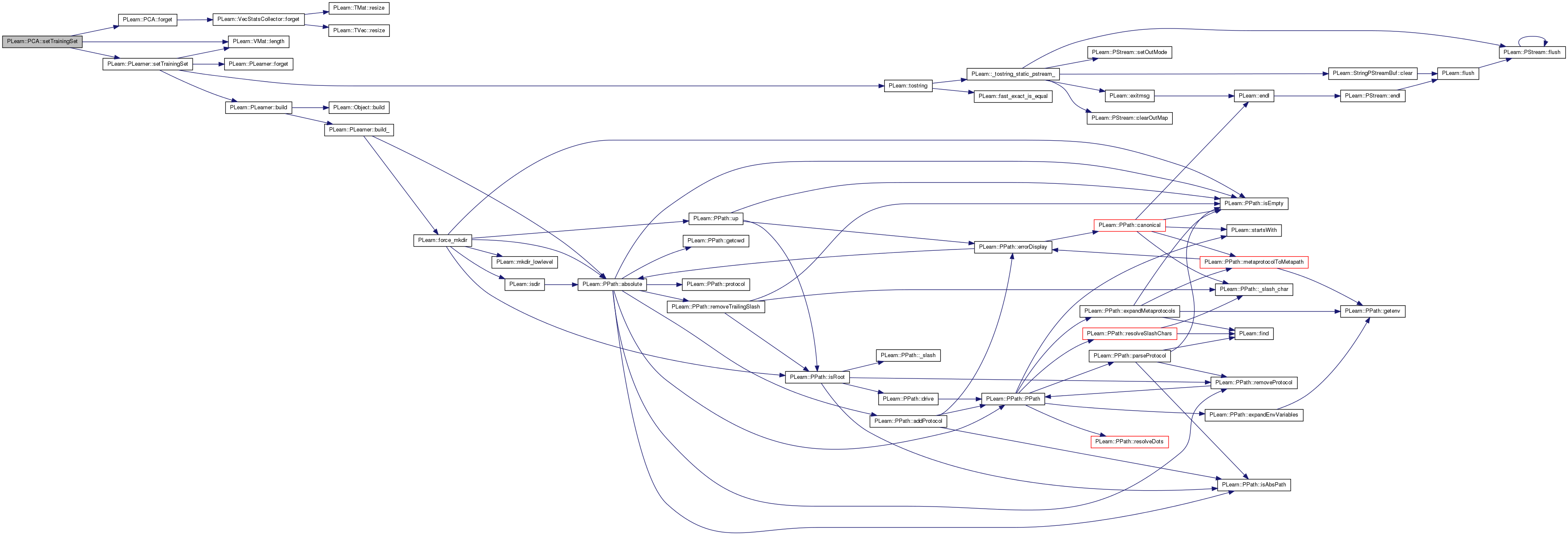
Set nstages to the training_set length under the 'incremental' algo.
Reimplemented from PLearn::PLearner.
Definition at line 236 of file PCA.cc.
References algo, forget(), PLearn::VMat::length(), PLearn::PLearner::nstages, and PLearn::PLearner::setTrainingSet().
Referenced by compare(), and em_algo().
{
inherited::setTrainingSet( training_set, call_forget );
// Even if call_forget is false, the classical PCA algorithm must start
// from scratch if the dataset changed. If call_forget is true, forget
// was already called by the inherited::setTrainingSet
if ( !call_forget && algo == "classical" )
forget();
if ( algo == "incremental" )
nstages = training_set.length();
}

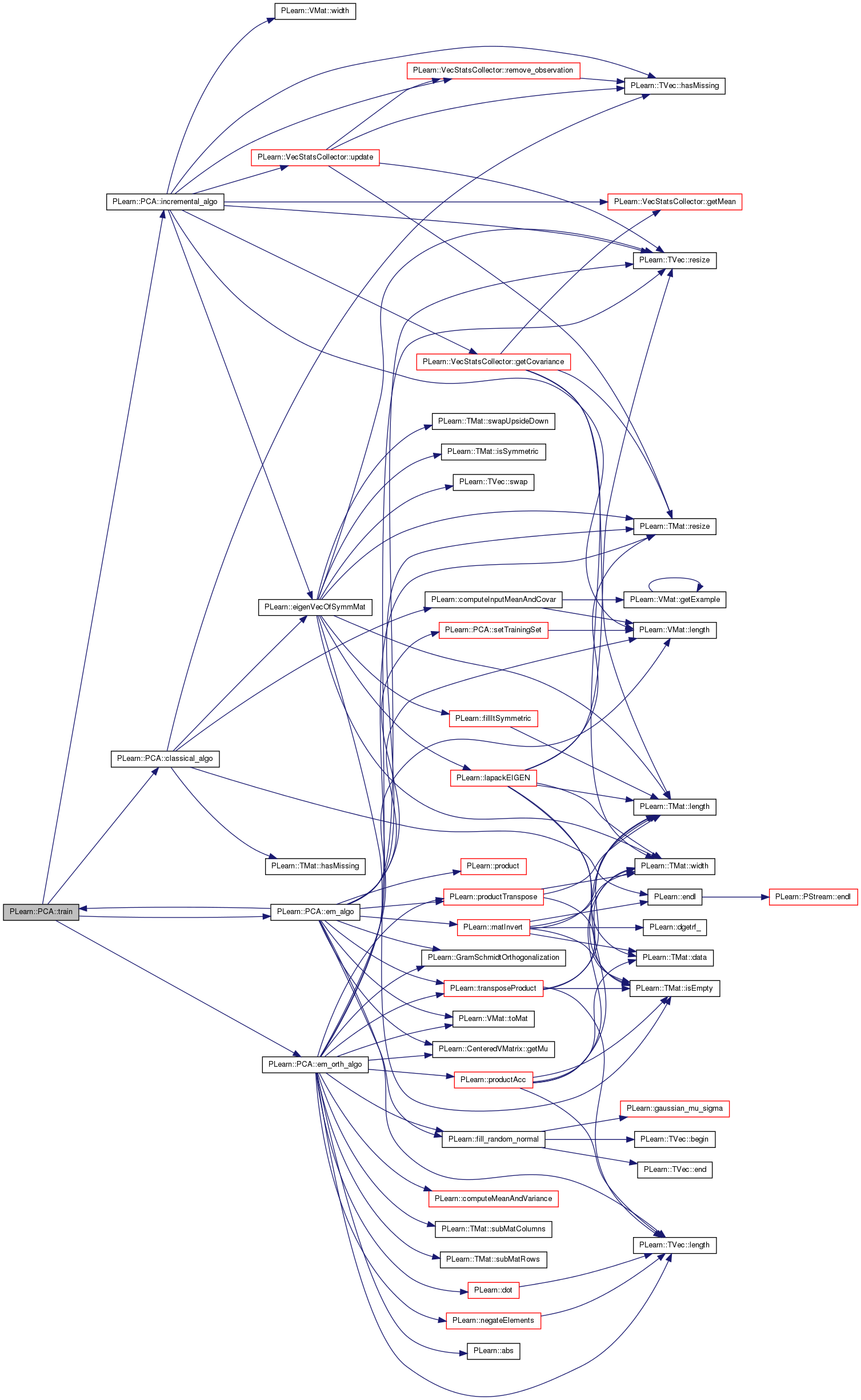
| void PLearn::PCA::train | ( | ) | [virtual] |
The role of the train method is to bring the learner up to stage==nstages, updating the train_stats collector with training costs measured on-line in the process.
Implements PLearn::PLearner.
Definition at line 560 of file PCA.cc.
References algo, classical_algo(), em_algo(), em_orth_algo(), incremental_algo(), PLearn::PLearner::nstages, PLERROR, PLWARNING, and PLearn::PLearner::stage.
Referenced by compare(), and em_algo().
{
if ( stage < nstages )
{
if ( algo == "classical" )
classical_algo( );
else if( algo == "incremental" )
incremental_algo();
else if ( algo == "em" )
em_algo();
else if ( algo == "em_orth" )
em_orth_algo( );
else
PLERROR("In PCA::train - Unknown value for 'algo'");
}
else
PLWARNING("In PCA::train - The learner has already been train, skipping training");
}
Incremental algorithm option: This option specifies a window over which the PCA should be done.
That is, if the length of the training set is greater than 'horizon', the observations that will effectively contribute to the covariance matrix will only be the last 'horizon' ones. All negative values being interpreted as 'keep all observations'.
Default: -1 (all observations are kept)
Definition at line 110 of file PCA.h.
Referenced by declareOptions(), incremental_algo(), and main().
VecStatsCollector PLearn::PCA::_incremental_stats [protected] |
Definition at line 56 of file PCA.h.
Referenced by build_(), forget(), and incremental_algo().
int PLearn::PCA::_oldest_observation [protected] |
Incremental algo:
The first time values are fed to _incremental_stats, we must remember the first observation in order not to remove observation that never contributed to the covariance matrix.
Initialized to -1;
Definition at line 67 of file PCA.h.
Referenced by declareOptions(), forget(), and incremental_algo().
Reimplemented from PLearn::PLearner.
| string PLearn::PCA::algo |
The algorithm used to perform the Principal Component Analysis:
Definition at line 99 of file PCA.h.
Referenced by build_(), declareOptions(), forget(), main(), setTrainingSet(), and train().
The ncomponents eigenvalues corresponding to the principal directions kept.
Definition at line 137 of file PCA.h.
Referenced by classical_algo(), compare(), computeOutput(), declareOptions(), em_algo(), em_orth_algo(), incremental_algo(), makeDeepCopyFromShallowCopy(), and reconstruct().
A ncomponents x inputsize matrix containing the principal eigenvectors.
Definition at line 140 of file PCA.h.
Referenced by classical_algo(), computeOutput(), declareOptions(), em_algo(), em_orth_algo(), incremental_algo(), makeDeepCopyFromShallowCopy(), and reconstruct().
If true, if a missing value is encountered on an input variable for a computeOutput, it is replaced by the estimated mu for that variable before projecting on the principal components.
Definition at line 126 of file PCA.h.
Referenced by computeOutput(), and declareOptions().
The (weighted) mean of the samples.
Definition at line 134 of file PCA.h.
Referenced by classical_algo(), computeOutput(), declareOptions(), em_algo(), em_orth_algo(), incremental_algo(), makeDeepCopyFromShallowCopy(), and reconstruct().
The number of principal components to keep (that's also the outputsize)
Definition at line 113 of file PCA.h.
Referenced by classical_algo(), computeOutput(), declareOptions(), em_algo(), em_orth_algo(), incremental_algo(), main(), and outputsize().
If true, we divide by sqrt(eigenval) after projecting on the eigenvec.
Definition at line 120 of file PCA.h.
Referenced by computeOutput(), declareOptions(), em_algo(), em_orth_algo(), and reconstruct().
Definition at line 121 of file PCA.h.
Referenced by build_(), declareOptions(), and main().
This gets added to the diagonal of the covariance matrix prior to eigen-decomposition (classical algorithm only)
Definition at line 117 of file PCA.h.
Referenced by classical_algo(), and declareOptions().
 1.7.4
1.7.4