|
PLearn 0.1
|
|
PLearn 0.1
|
Multi-layer neural network trained with an efficient Natural Gradient optimization. More...
#include <NatGradNNet.h>
Public Member Functions | |
| NatGradNNet () | |
| Stages for profiling the correlation between the gradients' elements. | |
| virtual int | outputsize () const |
| Returns the size of this learner's output, (which typically may depend on its inputsize(), targetsize() and set options). | |
| virtual void | forget () |
| (Re-)initializes the PLearner in its fresh state (that state may depend on the 'seed' option) and sets 'stage' back to 0 (this is the stage of a fresh learner!). | |
| virtual void | train () |
| The role of the train method is to bring the learner up to stage==nstages, updating the train_stats collector with training costs measured on-line in the process. | |
| virtual void | computeOutput (const Vec &input, Vec &output) const |
| Computes the output from the input. | |
| virtual void | computeOutputs (const Mat &input, Mat &output) const |
| if it is more efficient to compute multipe outputs simultaneously, it can be advantageous to define the latter instead, in which each row of the matrices is associated with one example. | |
| virtual void | computeOutputsAndCosts (const Mat &input, const Mat &target, Mat &output, Mat &costs) const |
| minibatch version of computeOutputAndCosts | |
| virtual void | computeCostsFromOutputs (const Vec &input, const Vec &output, const Vec &target, Vec &costs) const |
| Computes the costs from already computed output. | |
| virtual TVec< std::string > | getTestCostNames () const |
| Returns the names of the costs computed by computeCostsFromOutpus (and thus the test method). | |
| virtual TVec< std::string > | getTrainCostNames () const |
| Returns the names of the objective costs that the train method computes and for which it updates the VecStatsCollector train_stats. | |
| virtual string | classname () const |
| virtual OptionList & | getOptionList () const |
| virtual OptionMap & | getOptionMap () const |
| virtual RemoteMethodMap & | getRemoteMethodMap () const |
| virtual NatGradNNet * | deepCopy (CopiesMap &copies) const |
| virtual void | build () |
| Finish building the object; just call inherited::build followed by build_() | |
| virtual void | makeDeepCopyFromShallowCopy (CopiesMap &copies) |
| Transforms a shallow copy into a deep copy. | |
Static Public Member Functions | |
| static string | _classname_ () |
| static OptionList & | _getOptionList_ () |
| static RemoteMethodMap & | _getRemoteMethodMap_ () |
| static Object * | _new_instance_for_typemap_ () |
| static bool | _isa_ (const Object *o) |
| static void | _static_initialize_ () |
| static const PPath & | declaringFile () |
Public Attributes | |
| int | noutputs |
| TVec< int > | hidden_layer_sizes |
| sizes of hidden layers, provided by the user. | |
| TVec< Mat > | layer_params |
| layer_params[i] is a matrix of dimension layer_sizes[i+1] x (layer_sizes[i]+1) containing the neuron biases in its first column. | |
| TVec< Mat > | layer_mparams |
| mean layer_params, averaged over past updates (moving average) | |
| real | params_averaging_coeff |
| mparams <-- (1-params_averaging_coeff)mparams + params_averaging_coeff*params | |
| int | params_averaging_freq |
| how often (in terms of minibatches, i.e. weight updates) do we perform the above? | |
| real | init_lrate |
| initial learning rate | |
| real | lrate_decay |
| learning rate decay factor | |
| real | output_layer_L1_penalty_factor |
| L1 penalty applied to the output layer's parameters. | |
| real | output_layer_lrate_scale |
| scaling factor of the learning rate for the output layer | |
| int | minibatch_size |
| update the parameters only so often | |
| PP< GradientCorrector > | neurons_natgrad_template |
| natural gradient estimator for neurons (if 0 then do not correct the gradient on neurons) | |
| TVec< PP< GradientCorrector > > | neurons_natgrad_per_layer |
| PP< GradientCorrector > | params_natgrad_template |
| natural gradient estimator for the parameters within each neuron (if 0 then do not correct the gradient on each neuron weight) | |
| PP< GradientCorrector > | params_natgrad_per_input_template |
| natural gradient estimator solely for the parameters of the first layer. | |
| TVec< PP< GradientCorrector > > | params_natgrad_per_group |
| the above templates are used by the user to specifiy all the elements of the vector below | |
| PP< GradientCorrector > | full_natgrad |
| optionally, if neurons_natgrad==0 and params_natgrad_template==0, one can have regular stochastic gradient descent, or full-covariance natural gradient using the natural gradient estimator below | |
| string | output_type |
| type of output cost: "NLL" for classification problems, "MSE" for regression | |
| real | input_size_lrate_normalization_power |
| 0 does not scale the learning rate 1 scales it by 1 / the nb of inputs of the neuron 2 scales it by 1 / sqrt(the nb of inputs of the neuron) etc. | |
| real | lrate_scale_factor |
| scale the learning rate in different neurons by a factor taken randomly as follows: choose integer n uniformly between lrate_scale_factor_min_power and lrate_scale_factor_max_power inclusively, and then scale learning rate by lrate_scale_factor^n. | |
| int | lrate_scale_factor_max_power |
| int | lrate_scale_factor_min_power |
| bool | self_adjusted_scaling_and_bias |
| Let each neuron self-adjust its bias and scaling factor of its activations so that the mean and standard deviation of the activations reach the target_mean_activation and target_stdev_activation. | |
| real | target_mean_activation |
| real | target_stdev_activation |
| real | activation_statistics_moving_average_coefficient |
Static Public Attributes | |
| static StaticInitializer | _static_initializer_ |
Protected Member Functions | |
| void | onlineStep (int t, const Mat &targets, Mat &train_costs, Vec example_weights) |
| one minibatch training step | |
| void | fpropNet (int n_examples, bool during_training) const |
| compute a minibatch of size n_examples network top-layer output given layer 0 output (= network input) (note that log-probabilities are computed for classification tasks, output_type=NLL) | |
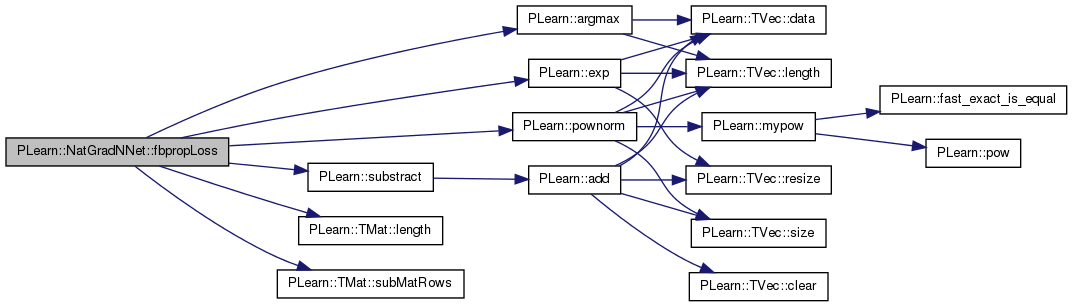
| void | fbpropLoss (const Mat &output, const Mat &target, const Vec &example_weights, Mat &train_costs) const |
| compute train costs given the network top-layer output and write into neuron_gradients_per_layer[n_layers-2], gradient on pre-non-linearity activation | |
Static Protected Member Functions | |
| static void | declareOptions (OptionList &ol) |
| Declares the class options. | |
Protected Attributes | |
| int | n_layers |
| number of layers of weights (2 for a neural net with one hidden layer) | |
| TVec< int > | layer_sizes |
| layer sizes (derived from hidden_layer_sizes, inputsize_ and outputsize_) | |
| TVec< Mat > | biases |
| pointers into the layer_params | |
| TVec< Mat > | weights |
| TVec< Mat > | mweights |
| TVec< Vec > | activations_scaling |
| TVec< Vec > | mean_activations |
| TVec< Vec > | var_activations |
| real | cumulative_training_time |
Private Types | |
| typedef PLearner | inherited |
Private Member Functions | |
| void | build_ () |
| This does the actual building. | |
Private Attributes | |
| Vec | all_params |
| Vec | all_params_delta |
| Vec | all_params_gradient |
| Vec | all_mparams |
| TVec< Mat > | layer_params_gradient |
| TVec< Vec > | layer_params_delta |
| TVec< Vec > | group_params |
| TVec< Vec > | group_params_delta |
| TVec< Vec > | group_params_gradient |
| Mat | neuron_gradients |
| TVec< Mat > | neuron_gradients_per_layer |
| TVec< Mat > | neuron_outputs_per_layer |
| TVec< Mat > | neuron_extended_outputs_per_layer |
| Mat | targets |
| Vec | example_weights |
| Mat | train_costs |
Multi-layer neural network trained with an efficient Natural Gradient optimization.
Definition at line 53 of file NatGradNNet.h.
typedef PLearner PLearn::NatGradNNet::inherited [private] |
Reimplemented from PLearn::PLearner.
Definition at line 55 of file NatGradNNet.h.
| PLearn::NatGradNNet::NatGradNNet | ( | ) |
Stages for profiling the correlation between the gradients' elements.
To see differences between class gradient covariances Holds the number of samples gathered for each weight
Definition at line 58 of file NatGradNNet.cc.
References PLearn::PLearner::random_gen.
: noutputs(-1), params_averaging_coeff(1.0), params_averaging_freq(5), init_lrate(0.01), lrate_decay(0), output_layer_L1_penalty_factor(0.0), output_layer_lrate_scale(1), minibatch_size(1), output_type("NLL"), input_size_lrate_normalization_power(0), lrate_scale_factor(3), lrate_scale_factor_max_power(0), lrate_scale_factor_min_power(0), self_adjusted_scaling_and_bias(false), target_mean_activation(-4), // target_stdev_activation(3), // 2.5% of the time we are above 1 //corr_profiling_start(0), //corr_profiling_end(0), n_layers(-1), cumulative_training_time(0) { random_gen = new PRandom(); }
| string PLearn::NatGradNNet::_classname_ | ( | ) | [static] |
Reimplemented from PLearn::PLearner.
Definition at line 56 of file NatGradNNet.cc.
| OptionList & PLearn::NatGradNNet::_getOptionList_ | ( | ) | [static] |
Reimplemented from PLearn::PLearner.
Definition at line 56 of file NatGradNNet.cc.
| RemoteMethodMap & PLearn::NatGradNNet::_getRemoteMethodMap_ | ( | ) | [static] |
Reimplemented from PLearn::PLearner.
Definition at line 56 of file NatGradNNet.cc.
Reimplemented from PLearn::PLearner.
Definition at line 56 of file NatGradNNet.cc.
| Object * PLearn::NatGradNNet::_new_instance_for_typemap_ | ( | ) | [static] |
Reimplemented from PLearn::Object.
Definition at line 56 of file NatGradNNet.cc.
| StaticInitializer NatGradNNet::_static_initializer_ & PLearn::NatGradNNet::_static_initialize_ | ( | ) | [static] |
Reimplemented from PLearn::PLearner.
Definition at line 56 of file NatGradNNet.cc.
| void PLearn::NatGradNNet::build | ( | ) | [virtual] |
Finish building the object; just call inherited::build followed by build_()
Reimplemented from PLearn::PLearner.
Definition at line 457 of file NatGradNNet.cc.
References PLearn::PLearner::build(), and build_().
Referenced by train().
{
inherited::build();
build_();
}

| void PLearn::NatGradNNet::build_ | ( | ) | [private] |
This does the actual building.
Reimplemented from PLearn::PLearner.
Definition at line 281 of file NatGradNNet.cc.
References PLearn::Profiler::activate(), activations_scaling, all_mparams, all_params, all_params_delta, all_params_gradient, biases, PLearn::deepCopy(), example_weights, PLearn::TVec< T >::fill(), getTrainCostNames(), group_params, group_params_delta, group_params_gradient, hidden_layer_sizes, i, PLearn::PLearner::inputsize_, j, layer_mparams, layer_params, layer_params_delta, layer_params_gradient, layer_sizes, PLearn::TVec< T >::length(), mean_activations, minibatch_size, mweights, n_layers, neuron_extended_outputs_per_layer, neuron_gradients, neuron_gradients_per_layer, neuron_outputs_per_layer, neurons_natgrad_per_layer, neurons_natgrad_template, noutputs, output_layer_L1_penalty_factor, output_type, params_natgrad_per_group, params_natgrad_per_input_template, params_natgrad_template, PLASSERT_MSG, PLERROR, PLWARNING, PLearn::TMat< T >::resize(), PLearn::TVec< T >::resize(), PLearn::TMat< T >::subMatColumns(), PLearn::TVec< T >::subVec(), PLearn::PLearner::targetsize_, PLearn::TVec< T >::toMat(), train_costs, PLearn::PLearner::train_set, var_activations, and weights.
Referenced by build().
{
if (!train_set)
return;
inputsize_ = train_set->inputsize();
if (output_type=="MSE")
{
if (noutputs<0) noutputs = targetsize_;
else PLASSERT_MSG(noutputs==targetsize_,"NatGradNNet: noutputs should be -1 or match data's targetsize");
}
else if (output_type=="NLL")
{
if (noutputs<0)
PLERROR("NatGradNNet: if output_type=NLL (classification), one \n"
"should provide noutputs = number of classes, or possibly\n"
"1 when 2 classes\n");
}
else if (output_type=="cross_entropy")
{
if(noutputs!=1)
PLERROR("NatGradNNet: if output_type=cross_entropy, then \n"
"noutputs should be 1.\n");
}
else PLERROR("NatGradNNet: output_type should be cross_entropy, NLL or MSE\n");
if( output_layer_L1_penalty_factor < 0. )
PLWARNING("NatGradNNet::build_ - output_layer_L1_penalty_factor is negative!\n");
while (hidden_layer_sizes.length()>0 && hidden_layer_sizes[hidden_layer_sizes.length()-1]==0)
hidden_layer_sizes.resize(hidden_layer_sizes.length()-1);
n_layers = hidden_layer_sizes.length()+2;
layer_sizes.resize(n_layers);
layer_sizes.subVec(1,n_layers-2) << hidden_layer_sizes;
layer_sizes[0]=inputsize_;
layer_sizes[n_layers-1]=noutputs;
layer_params.resize(n_layers-1);
layer_mparams.resize(n_layers-1);
layer_params_delta.resize(n_layers-1);
layer_params_gradient.resize(n_layers-1);
biases.resize(n_layers-1);
activations_scaling.resize(n_layers-1);
weights.resize(n_layers-1);
mweights.resize(n_layers-1);
mean_activations.resize(n_layers-1);
var_activations.resize(n_layers-1);
int n_neurons=0;
int n_params=0;
for (int i=0;i<n_layers-1;i++)
{
n_neurons+=layer_sizes[i+1];
n_params+=layer_sizes[i+1]*(1+layer_sizes[i]);
}
all_params.resize(n_params);
all_mparams.resize(n_params);
all_params_gradient.resize(n_params);
all_params_delta.resize(n_params);
//all_params_cum_gradient.resize(n_params); // *stat*
// depending on how parameters are grouped on the first layer
int n_groups = params_natgrad_per_input_template ? (n_neurons-layer_sizes[1]+layer_sizes[0]+1) : n_neurons;
group_params.resize(n_groups);
group_params_delta.resize(n_groups);
group_params_gradient.resize(n_groups);
for (int i=0,k=0,p=0;i<n_layers-1;i++)
{
int np=layer_sizes[i+1]*(1+layer_sizes[i]);
// First layer has natural gradient applied on groups of parameters
// linked to the same input -> parameters must be stored TRANSPOSED!
if( i==0 && params_natgrad_per_input_template ) {
layer_params[i]=all_params.subVec(p,np).toMat(layer_sizes[i]+1,layer_sizes[i+1]);
layer_mparams[i]=all_mparams.subVec(p,np).toMat(layer_sizes[i]+1,layer_sizes[i+1]);
biases[i]=layer_params[i].subMatRows(0,1);
weights[i]=layer_params[i].subMatRows(1,layer_sizes[i]); //weights[0] from layer 0 to layer 1
mweights[i]=layer_mparams[i].subMatRows(1,layer_sizes[i]); //weights[0] from layer 0 to layer 1
layer_params_gradient[i]=all_params_gradient.subVec(p,np).toMat(layer_sizes[i]+1,layer_sizes[i+1]);
layer_params_delta[i]=all_params_delta.subVec(p,np);
for (int j=0;j<layer_sizes[i]+1;j++,k++) // include a bias input
{
group_params[k]=all_params.subVec(p,layer_sizes[i+1]);
group_params_delta[k]=all_params_delta.subVec(p,layer_sizes[i+1]);
group_params_gradient[k]=all_params_gradient.subVec(p,layer_sizes[i+1]);
p+=layer_sizes[i+1];
}
// Usual parameter storage
} else {
layer_params[i]=all_params.subVec(p,np).toMat(layer_sizes[i+1],layer_sizes[i]+1);
layer_mparams[i]=all_mparams.subVec(p,np).toMat(layer_sizes[i+1],layer_sizes[i]+1);
biases[i]=layer_params[i].subMatColumns(0,1);
weights[i]=layer_params[i].subMatColumns(1,layer_sizes[i]); // weights[0] from layer 0 to layer 1
mweights[i]=layer_mparams[i].subMatColumns(1,layer_sizes[i]); // weights[0] from layer 0 to layer 1
layer_params_gradient[i]=all_params_gradient.subVec(p,np).toMat(layer_sizes[i+1],layer_sizes[i]+1);
layer_params_delta[i]=all_params_delta.subVec(p,np);
for (int j=0;j<layer_sizes[i+1];j++,k++)
{
group_params[k]=all_params.subVec(p,1+layer_sizes[i]);
group_params_delta[k]=all_params_delta.subVec(p,1+layer_sizes[i]);
group_params_gradient[k]=all_params_gradient.subVec(p,1+layer_sizes[i]);
p+=1+layer_sizes[i];
}
}
activations_scaling[i].resize(layer_sizes[i+1]);
mean_activations[i].resize(layer_sizes[i+1]);
var_activations[i].resize(layer_sizes[i+1]);
}
if (params_natgrad_template || params_natgrad_per_input_template)
{
int n_input_groups=0;
int n_neuron_groups=0;
if(params_natgrad_template)
n_neuron_groups = n_neurons;
if( params_natgrad_per_input_template ) {
n_input_groups = layer_sizes[0]+1;
if(params_natgrad_template) // override first layer groups if present
n_neuron_groups -= layer_sizes[1];
}
params_natgrad_per_group.resize(n_input_groups+n_neuron_groups);
for (int i=0;i<n_input_groups;i++)
params_natgrad_per_group[i] = PLearn::deepCopy(params_natgrad_per_input_template);
for (int i=n_input_groups; i<n_input_groups+n_neuron_groups;i++)
params_natgrad_per_group[i] = PLearn::deepCopy(params_natgrad_template);
}
if (neurons_natgrad_template && neurons_natgrad_per_layer.length()==0)
{
neurons_natgrad_per_layer.resize(n_layers); // 0 not used
for (int i=1;i<n_layers;i++) // no need for correcting input layer
neurons_natgrad_per_layer[i] = PLearn::deepCopy(neurons_natgrad_template);
}
neuron_gradients.resize(minibatch_size,n_neurons);
neuron_outputs_per_layer.resize(n_layers); // layer 0 = input, layer n_layers-1 = output
neuron_extended_outputs_per_layer.resize(n_layers); // layer 0 = input, layer n_layers-1 = output
neuron_gradients_per_layer.resize(n_layers); // layer 0 not used
neuron_extended_outputs_per_layer[0].resize(minibatch_size,1+layer_sizes[0]);
neuron_outputs_per_layer[0]=neuron_extended_outputs_per_layer[0].subMatColumns(1,layer_sizes[0]);
neuron_extended_outputs_per_layer[0].column(0).fill(1.0); // for biases
for (int i=1,k=0;i<n_layers;k+=layer_sizes[i],i++)
{
neuron_extended_outputs_per_layer[i].resize(minibatch_size,1+layer_sizes[i]);
neuron_outputs_per_layer[i]=neuron_extended_outputs_per_layer[i].subMatColumns(1,layer_sizes[i]);
neuron_extended_outputs_per_layer[i].column(0).fill(1.0); // for biases
neuron_gradients_per_layer[i] =
neuron_gradients.subMatColumns(k,layer_sizes[i]);
}
example_weights.resize(minibatch_size);
TVec<string> train_cost_names = getTrainCostNames() ;
train_costs.resize(minibatch_size,train_cost_names.length()-2 );
Profiler::activate();
// Gradient correlation profiling
//if( corr_profiling_start != corr_profiling_end ) {
// PLASSERT( (0<=corr_profiling_start) && (corr_profiling_start<corr_profiling_end) );
// cout << "n_params " << n_params << endl;
// // Build the names.
// stringstream ss_suffix;
// for (int i=0;i<n_layers;i++) {
// ss_suffix << "_" << layer_sizes[i];
// }
// ss_suffix << "_stages_" << corr_profiling_start << "_" << corr_profiling_end;
// string str_gc_name = "gCcorr" + ss_suffix.str();
// string str_ngc_name;
// if( full_natgrad ) {
// str_ngc_name = "ngCcorr_full" + ss_suffix.str();
// } else if (params_natgrad_template) {
// str_ngc_name = "ngCcorr_params" + ss_suffix.str();
// }
// // Build the profilers.
// g_corrprof = new CorrelationProfiler( n_params, str_gc_name);
// g_corrprof->build();
// ng_corrprof = new CorrelationProfiler( n_params, str_ngc_name);
// ng_corrprof->build();
//}
}

| string PLearn::NatGradNNet::classname | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 56 of file NatGradNNet.cc.
Referenced by train().

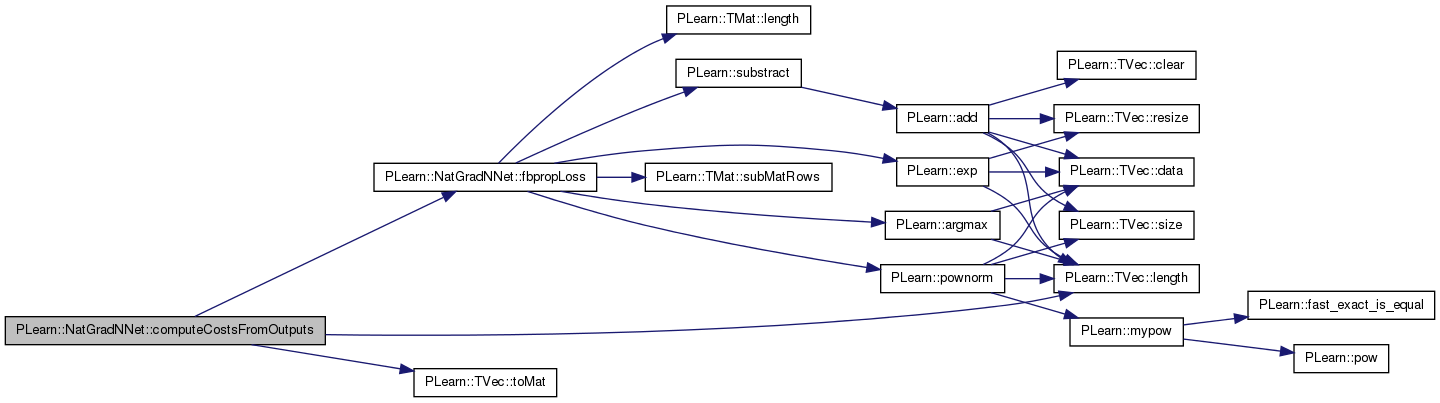
| void PLearn::NatGradNNet::computeCostsFromOutputs | ( | const Vec & | input, |
| const Vec & | output, | ||
| const Vec & | target, | ||
| Vec & | costs | ||
| ) | const [virtual] |
Computes the costs from already computed output.
Implements PLearn::PLearner.
Definition at line 1022 of file NatGradNNet.cc.
References fbpropLoss(), PLearn::TVec< T >::length(), PLearn::TVec< T >::toMat(), and w.
{
Vec w(1);
w[0]=1;
Mat outputM = output.toMat(1,output.length());
Mat targetM = target.toMat(1,output.length());
Mat costsM = costs.toMat(1,costs.length());
fbpropLoss(outputM,targetM,w,costsM);
}
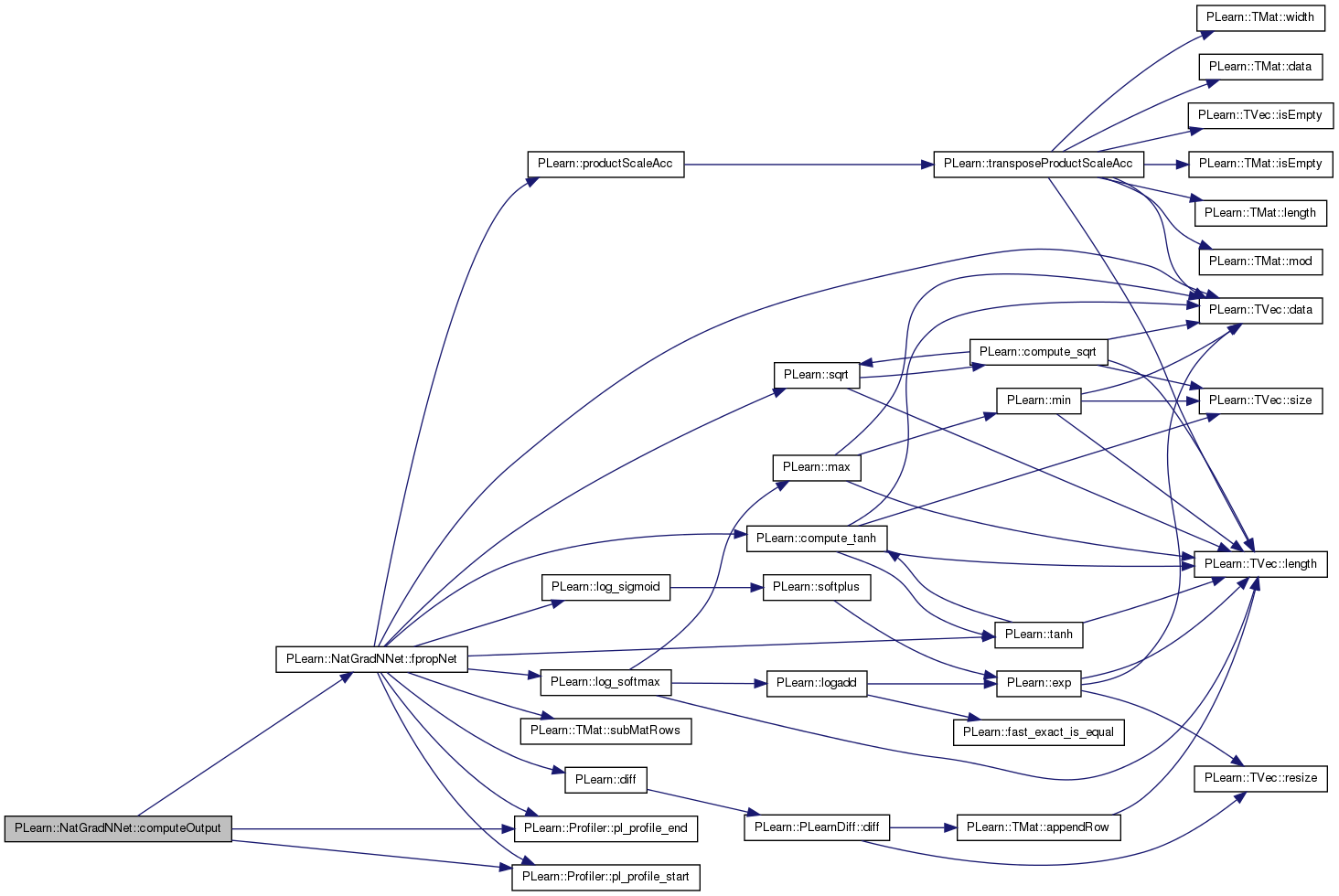
Computes the output from the input.
Reimplemented from PLearn::PLearner.
Definition at line 830 of file NatGradNNet.cc.
References fpropNet(), n_layers, neuron_outputs_per_layer, PLearn::Profiler::pl_profile_end(), and PLearn::Profiler::pl_profile_start().
{
Profiler::pl_profile_start("NatGradNNet::computeOutput");
neuron_outputs_per_layer[0](0) << input;
fpropNet(1,false);
output << neuron_outputs_per_layer[n_layers-1](0);
Profiler::pl_profile_end("NatGradNNet::computeOutput");
}
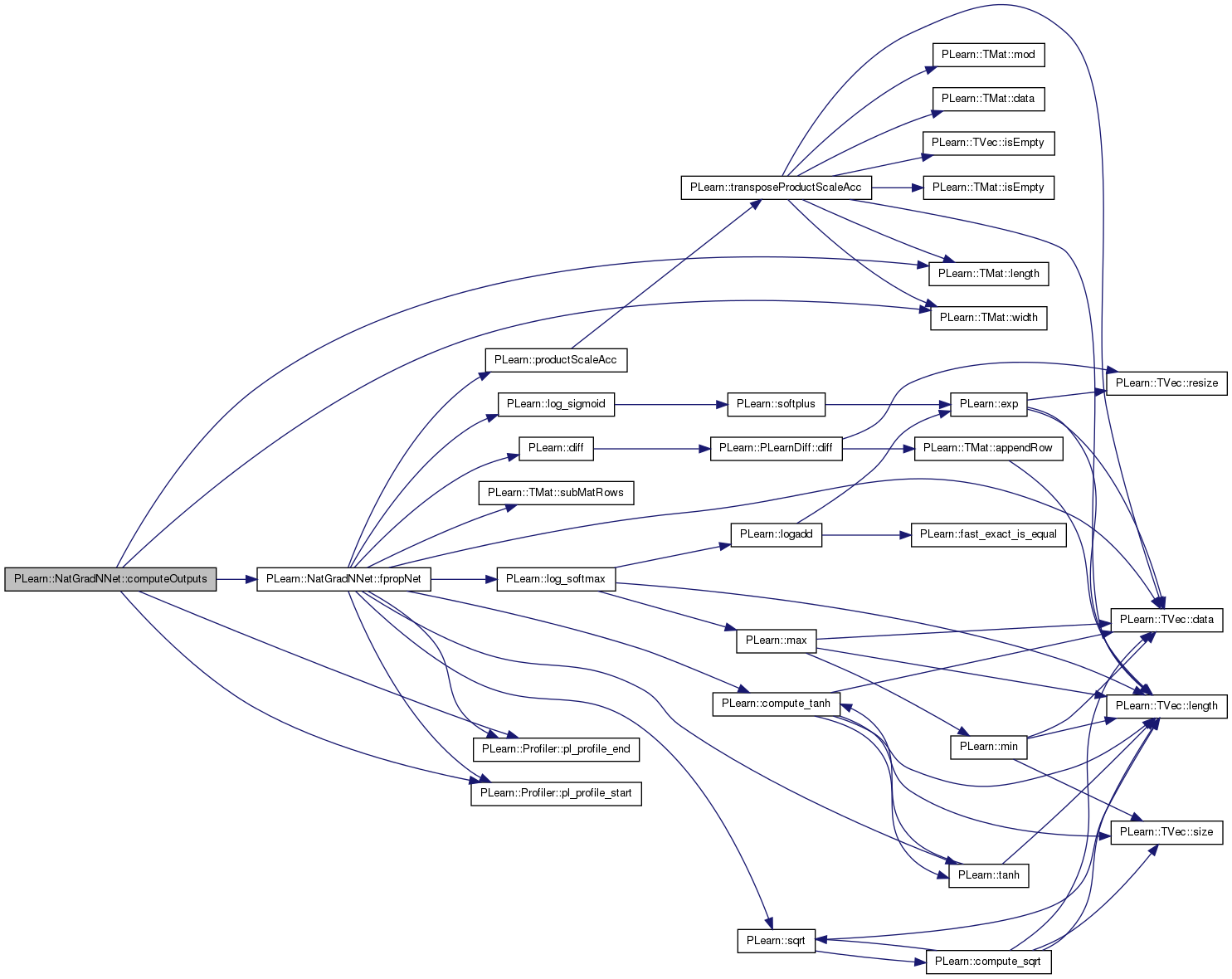
if it is more efficient to compute multipe outputs simultaneously, it can be advantageous to define the latter instead, in which each row of the matrices is associated with one example.
Reimplemented from PLearn::PLearner.
Definition at line 1049 of file NatGradNNet.cc.
References fpropNet(), PLearn::TMat< T >::length(), minibatch_size, n_layers, neuron_outputs_per_layer, PLearn::Profiler::pl_profile_end(), PLearn::Profiler::pl_profile_start(), PLASSERT, PLearn::PLearner::test_minibatch_size, and PLearn::TMat< T >::width().
Referenced by computeOutputsAndCosts().
{
Profiler::pl_profile_start("NatGradNNet::computeOutputs");
PLASSERT(test_minibatch_size<=minibatch_size);
neuron_outputs_per_layer[0].subMat(0,0,input.length(),input.width()) << input;
fpropNet(input.length(),false);
output << neuron_outputs_per_layer[n_layers-1].subMat(0,0,output.length(),output.width());
Profiler::pl_profile_end("NatGradNNet::computeOutputs");
}

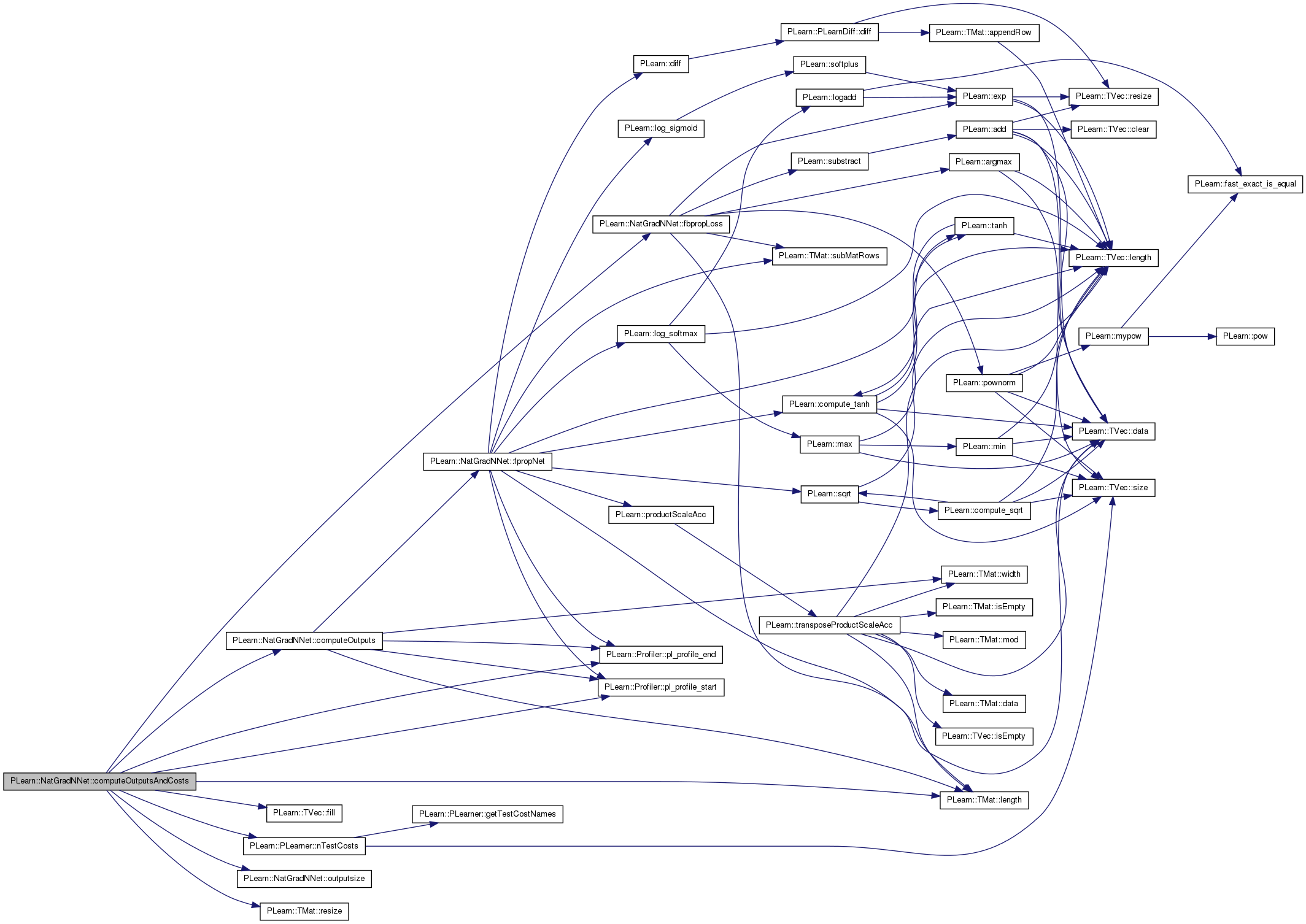
| void PLearn::NatGradNNet::computeOutputsAndCosts | ( | const Mat & | input, |
| const Mat & | target, | ||
| Mat & | output, | ||
| Mat & | costs | ||
| ) | const [virtual] |
minibatch version of computeOutputAndCosts
Reimplemented from PLearn::PLearner.
Definition at line 1058 of file NatGradNNet.cc.
References computeOutputs(), fbpropLoss(), PLearn::TVec< T >::fill(), PLearn::TMat< T >::length(), n, PLearn::PLearner::nTestCosts(), outputsize(), PLearn::Profiler::pl_profile_end(), PLearn::Profiler::pl_profile_start(), PLASSERT, PLearn::TMat< T >::resize(), and w.
{//TODO
Profiler::pl_profile_start("NatGradNNet::computeOutputsAndCosts");
int n=input.length();
PLASSERT(target.length()==n);
output.resize(n,outputsize());
costs.resize(n,nTestCosts());
computeOutputs(input,output);
Vec w(n);
w.fill(1);
fbpropLoss(output,target,w,costs);
Profiler::pl_profile_end("NatGradNNet::computeOutputsAndCosts");
}
| void PLearn::NatGradNNet::declareOptions | ( | OptionList & | ol | ) | [static, protected] |
Declares the class options.
Reimplemented from PLearn::PLearner.
Definition at line 83 of file NatGradNNet.cc.
References activation_statistics_moving_average_coefficient, activations_scaling, PLearn::OptionBase::buildoption, cumulative_training_time, PLearn::declareOption(), PLearn::PLearner::declareOptions(), full_natgrad, hidden_layer_sizes, init_lrate, input_size_lrate_normalization_power, layer_mparams, layer_params, layer_sizes, PLearn::OptionBase::learntoption, lrate_decay, lrate_scale_factor, lrate_scale_factor_max_power, lrate_scale_factor_min_power, minibatch_size, n_layers, neurons_natgrad_per_layer, neurons_natgrad_template, noutputs, output_layer_L1_penalty_factor, output_layer_lrate_scale, output_type, params_averaging_coeff, params_averaging_freq, params_natgrad_per_group, params_natgrad_per_input_template, params_natgrad_template, self_adjusted_scaling_and_bias, target_mean_activation, and target_stdev_activation.
{
declareOption(ol, "noutputs", &NatGradNNet::noutputs,
OptionBase::buildoption,
"Number of outputs of the neural network, which can be derived from output_type and targetsize_\n");
declareOption(ol, "n_layers", &NatGradNNet::n_layers,
OptionBase::learntoption,
"Number of layers of weights (ie. 2 for a neural net with one hidden layer).\n"
"Needs not be specified explicitly (derived from hidden_layer_sizes).\n");
declareOption(ol, "hidden_layer_sizes", &NatGradNNet::hidden_layer_sizes,
OptionBase::buildoption,
"Defines the architecture of the multi-layer neural network by\n"
"specifying the number of hidden units in each hidden layer.\n");
declareOption(ol, "layer_sizes", &NatGradNNet::layer_sizes,
OptionBase::learntoption,
"Derived from hidden_layer_sizes, inputsize_ and noutputs\n");
declareOption(ol, "cumulative_training_time", &NatGradNNet::cumulative_training_time,
OptionBase::learntoption,
"Cumulative training time since age=0, in seconds.\n");
declareOption(ol, "layer_params", &NatGradNNet::layer_params,
OptionBase::learntoption,
"Parameters used while training, for each layer, organized as follows: layer_params[i] \n"
"is a matrix of dimension layer_sizes[i+1] x (layer_sizes[i]+1)\n"
"containing the neuron biases in its first column.\n");
declareOption(ol, "activations_scaling", &NatGradNNet::activations_scaling,
OptionBase::learntoption,
"Scaling coefficients for each neuron of each layer, if self_adjusted_scaling_and_bias:\n"
" output = tanh(activations_scaling[layer][neuron] * (biases[layer][neuron] + weights[layer]*input[layer-1])\n");
declareOption(ol, "layer_mparams", &NatGradNNet::layer_mparams,
OptionBase::learntoption,
"Test parameters for each layer, organized like layer_params.\n"
"This is a moving average of layer_params, computed with\n"
"coefficient params_averaging_coeff. Thus the mparams are\n"
"a smoothed version of the params, and they are used only\n"
"during testing.\n");
declareOption(ol, "params_averaging_coeff", &NatGradNNet::params_averaging_coeff,
OptionBase::buildoption,
"Coefficient used to control how fast we forget old parameters\n"
"in the moving average performed as follows:\n"
"mparams <-- (1-params_averaging_coeff)mparams + params_averaging_coeff*params\n");
declareOption(ol, "params_averaging_freq", &NatGradNNet::params_averaging_freq,
OptionBase::buildoption,
"How often (in terms of number of minibatches, i.e. weight updates)\n"
"do we perform the moving average update calculation\n"
"mparams <-- (1-params_averaging_coeff)mparams + params_averaging_coeff*params\n");
declareOption(ol, "init_lrate", &NatGradNNet::init_lrate,
OptionBase::buildoption,
"Initial learning rate\n");
declareOption(ol, "lrate_decay", &NatGradNNet::lrate_decay,
OptionBase::buildoption,
"Learning rate decay factor\n");
declareOption(ol, "output_layer_L1_penalty_factor",
&NatGradNNet::output_layer_L1_penalty_factor,
OptionBase::buildoption,
"Optional (default=0) factor of L1 regularization term, i.e.\n"
"minimize L1_penalty_factor * sum_{ij} |weights(i,j)| during training.\n"
"Gets multiplied by the learning rate. Only on output layer!!");
declareOption(ol, "output_layer_lrate_scale", &NatGradNNet::output_layer_lrate_scale,
OptionBase::buildoption,
"Scaling factor of the learning rate for the output layer. Values less than 1"
"mean that the output layer parameters have a smaller learning rate than the others.\n");
declareOption(ol, "minibatch_size", &NatGradNNet::minibatch_size,
OptionBase::buildoption,
"Update the parameters only so often (number of examples).\n"
"Must be greater or equal to test_minibatch_size\n");
declareOption(ol, "neurons_natgrad_template", &NatGradNNet::neurons_natgrad_template,
OptionBase::buildoption,
"Optional template GradientCorrector for the neurons gradient.\n"
"If not provided, then the natural gradient correction\n"
"on the neurons gradient is not performed.\n");
declareOption(ol, "neurons_natgrad_per_layer",
&NatGradNNet::neurons_natgrad_per_layer,
OptionBase::learntoption,
"Vector of GradientCorrector objects for the gradient on the neurons of each layer.\n"
"They are copies of the neuron_natgrad_template provided by the user.\n");
declareOption(ol, "params_natgrad_template",
&NatGradNNet::params_natgrad_template,
OptionBase::buildoption,
"Optional template GradientCorrector object for the gradient of the parameters inside each neuron\n"
"It is replicated in the params_natgrad vector, for each neuron\n"
"If not provided, then the neuron-specific natural gradient estimator is not used.\n");
declareOption(ol, "params_natgrad_per_input_template",
&NatGradNNet::params_natgrad_per_input_template,
OptionBase::buildoption,
"Optional template GradientCorrector object for the gradient of the parameters of the first layer\n"
"grouped based upon their input. It is replicated in the params_natgrad_per_group vector, for each group.\n"
"If provided, overides the params_natgrad_template for the parameters of the first layer.\n");
declareOption(ol, "params_natgrad_per_group",
&NatGradNNet::params_natgrad_per_group,
OptionBase::learntoption,
"Vector of GradientCorrector objects for the gradient inside groups of parameters.\n"
"They are copies of the params_natgrad_template and params_natgrad_per_input_template\n"
"templates provided by the user.\n");
declareOption(ol, "full_natgrad", &NatGradNNet::full_natgrad,
OptionBase::buildoption,
"GradientCorrector for all the parameter gradients simultaneously.\n"
"This should not be set if neurons_natgrad or params_natgrad_template\n"
"is provided. If none of the GradientCorrectors is provided, then\n"
"regular stochastic gradient is performed.\n");
declareOption(ol, "output_type",
&NatGradNNet::output_type,
OptionBase::buildoption,
"type of output cost: 'cross_entropy' for binary classification,\n"
"'NLL' for classification problems(noutputs>=1),"
" 'cross_entropy' for classification(noutputs==1)"
" or 'MSE' for regression.\n");
declareOption(ol, "input_size_lrate_normalization_power",
&NatGradNNet::input_size_lrate_normalization_power,
OptionBase::buildoption,
"Scale the learning rate neuron-wise (or layer-wise actually, here):\n"
"-1 scales by 1 / ||x||^2, where x is the 1-extended input vector of the neuron\n"
"0 does not scale the learning rate\n"
"1 scales it by 1 / the nb of inputs of the neuron\n"
"2 scales it by 1 / sqrt(the nb of inputs of the neuron), etc.\n");
declareOption(ol, "lrate_scale_factor",
&NatGradNNet::lrate_scale_factor,
OptionBase::buildoption,
"scale the learning rate in different neurons by a factor\n"
"taken randomly as follows: choose integer n uniformly between\n"
"lrate_scale_factor_min_power and lrate_scale_factor_max_power\n"
"inclusively, and then scale learning rate by lrate_scale_factor^n.\n");
declareOption(ol, "lrate_scale_factor_max_power",
&NatGradNNet::lrate_scale_factor_max_power,
OptionBase::buildoption,
"See help on lrate_scale_factor\n");
declareOption(ol, "lrate_scale_factor_min_power",
&NatGradNNet::lrate_scale_factor_min_power,
OptionBase::buildoption,
"See help on lrate_scale_factor\n");
declareOption(ol, "self_adjusted_scaling_and_bias",
&NatGradNNet::self_adjusted_scaling_and_bias,
OptionBase::buildoption,
"If true, let each neuron self-adjust its bias and scaling factor\n"
"of its activations so that the mean and standard deviation of the\n"
"activations reach the target_mean_activation and target_stdev_activation.\n"
"The activations mean and variance are estimated by a moving average with\n"
"coefficient given by activations_statistics_moving_average_coefficient\n");
declareOption(ol, "target_mean_activation",
&NatGradNNet::target_mean_activation,
OptionBase::buildoption,
"See help on self_adjusted_scaling_and_bias\n");
declareOption(ol, "target_stdev_activation",
&NatGradNNet::target_stdev_activation,
OptionBase::buildoption,
"See help on self_adjusted_scaling_and_bias\n");
declareOption(ol, "activation_statistics_moving_average_coefficient",
&NatGradNNet::activation_statistics_moving_average_coefficient,
OptionBase::buildoption,
"The activations mean and variance used for self_adjusted_scaling_and_bias\n"
"are estimated by a moving average with this coefficient:\n"
" xbar <-- coefficient * xbar + (1-coefficient) x\n"
"where x could be the activation or its square\n");
//declareOption(ol, "corr_profiling_start",
// &NatGradNNet::corr_profiling_start,
// OptionBase::buildoption,
// "Stage to start the profiling of the gradients' and the\n"
// "natural gradients' correlation.\n");
//declareOption(ol, "corr_profiling_end",
// &NatGradNNet::corr_profiling_end,
// OptionBase::buildoption,
// "Stage to end the profiling of the gradients' and the\n"
// "natural gradients' correlations.\n");
// Now call the parent class' declareOptions
inherited::declareOptions(ol);
}

| static const PPath& PLearn::NatGradNNet::declaringFile | ( | ) | [inline, static] |
Reimplemented from PLearn::PLearner.
Definition at line 235 of file NatGradNNet.h.
:
//##### Protected Options ###############################################
| NatGradNNet * PLearn::NatGradNNet::deepCopy | ( | CopiesMap & | copies | ) | const [virtual] |
Reimplemented from PLearn::PLearner.
Definition at line 56 of file NatGradNNet.cc.
| void PLearn::NatGradNNet::fbpropLoss | ( | const Mat & | output, |
| const Mat & | target, | ||
| const Vec & | example_weights, | ||
| Mat & | train_costs | ||
| ) | const [protected] |
compute train costs given the network top-layer output and write into neuron_gradients_per_layer[n_layers-2], gradient on pre-non-linearity activation
compute train costs given the (pre-final-non-linearity) network top-layer output
Definition at line 955 of file NatGradNNet.cc.
References PLearn::argmax(), PLearn::exp(), grad, i, PLearn::TMat< T >::length(), minibatch_size, PLearn::PLearner::n_examples, n_layers, neuron_gradients_per_layer, noutputs, output_type, pl_log, PLERROR, PLearn::pownorm(), PLearn::TMat< T >::subMatRows(), and PLearn::substract().
Referenced by computeCostsFromOutputs(), computeOutputsAndCosts(), and onlineStep().
{
int n_examples = output.length();
Mat out_grad = neuron_gradients_per_layer[n_layers-1];
if (n_examples!=minibatch_size)
out_grad = out_grad.subMatRows(0,n_examples);
if (output_type=="NLL")
{
for (int i=0;i<n_examples;i++)
{
int target_class = int(round(target(i,0)));
#ifdef BOUNDCHECK
if(target_class>=noutputs)
PLERROR("In NatGradNNet::fbpropLoss one target value %d is higher then allowed by nout %d",
target_class, noutputs);
#endif
Vec outp = output(i);
Vec grad = out_grad(i);
exp(outp,grad); // map log-prob to prob
costs(i,0) = -outp[target_class];
costs(i,1) = (target_class == argmax(outp))?0:1;
grad[target_class]-=1;
costs(i,0) *= example_weight[i];
costs(i,2) = costs(i,1) * example_weight[i];
grad *= example_weight[i];
}
}
else if(output_type=="cross_entropy") {
for (int i=0;i<n_examples;i++)
{
int target_class = int(round(target(i,0)));
Vec outp = output(i);
Vec grad = out_grad(i);
exp(outp,grad); // map log-prob to prob
if( target_class == 1 ) {
costs(i,0) = - outp[0];
costs(i,1) = (grad[0]>0.5)?0:1;
} else {
costs(i,0) = - pl_log( 1.0 - grad[0] );
costs(i,1) = (grad[0]>0.5)?1:0;
}
grad[0] -= (real)target_class;
costs(i,0) *= example_weight[i];
costs(i,2) = costs(i,1) * example_weight[i];
grad *= example_weight[i];
}
//cout << "costs\t" << costs(0) << endl;
//cout << "gradient\t" << out_grad(0) << endl;
}
else // if (output_type=="MSE")
{
substract(output,target,out_grad);
for (int i=0;i<n_examples;i++)
{
costs(i,0) = pownorm(out_grad(i));
if (example_weight[i]!=1.0)
{
out_grad(i) *= example_weight[i];
costs(i,0) *= example_weight[i];
}
}
}
}

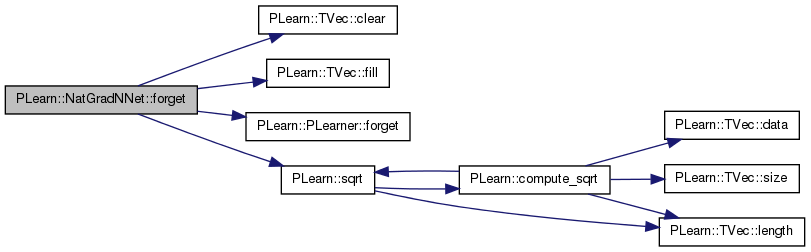
| void PLearn::NatGradNNet::forget | ( | ) | [virtual] |
(Re-)initializes the PLearner in its fresh state (that state may depend on the 'seed' option) and sets 'stage' back to 0 (this is the stage of a fresh learner!).
(Re-)initialize the PLearner in its fresh state (that state may depend on the 'seed' option) and sets 'stage' back to 0 (this is the stage of a fresh learner!)
Reimplemented from PLearn::PLearner.
Definition at line 510 of file NatGradNNet.cc.
References activations_scaling, all_mparams, all_params, biases, PLearn::TVec< T >::clear(), cumulative_training_time, PLearn::TVec< T >::fill(), PLearn::PLearner::forget(), i, layer_sizes, mean_activations, n_layers, params_averaging_coeff, PLearn::PLearner::random_gen, PLearn::sqrt(), PLearn::PLearner::stage, var_activations, and weights.
{
inherited::forget();
for (int i=0;i<n_layers-1;i++)
{
real delta = 1/sqrt(real(layer_sizes[i]));
random_gen->fill_random_uniform(weights[i],-delta,delta);
biases[i].clear();
activations_scaling[i].fill(1.0);
mean_activations[i].clear();
var_activations[i].fill(1.0);
}
stage = 0;
cumulative_training_time=0;
if (params_averaging_coeff!=1.0)
all_mparams << all_params;
// *stat*
/*if( pa_gradstats.length() == 0 ) {
pa_gradstats.resize(noutputs);
for(int i=0; i<noutputs; i++) {
(pa_gradstats[i]).compute_covariance = true;
}
} else {
for(int i=0; i<noutputs; i++) {
(pa_gradstats[i]).forget();
}
}*/
}
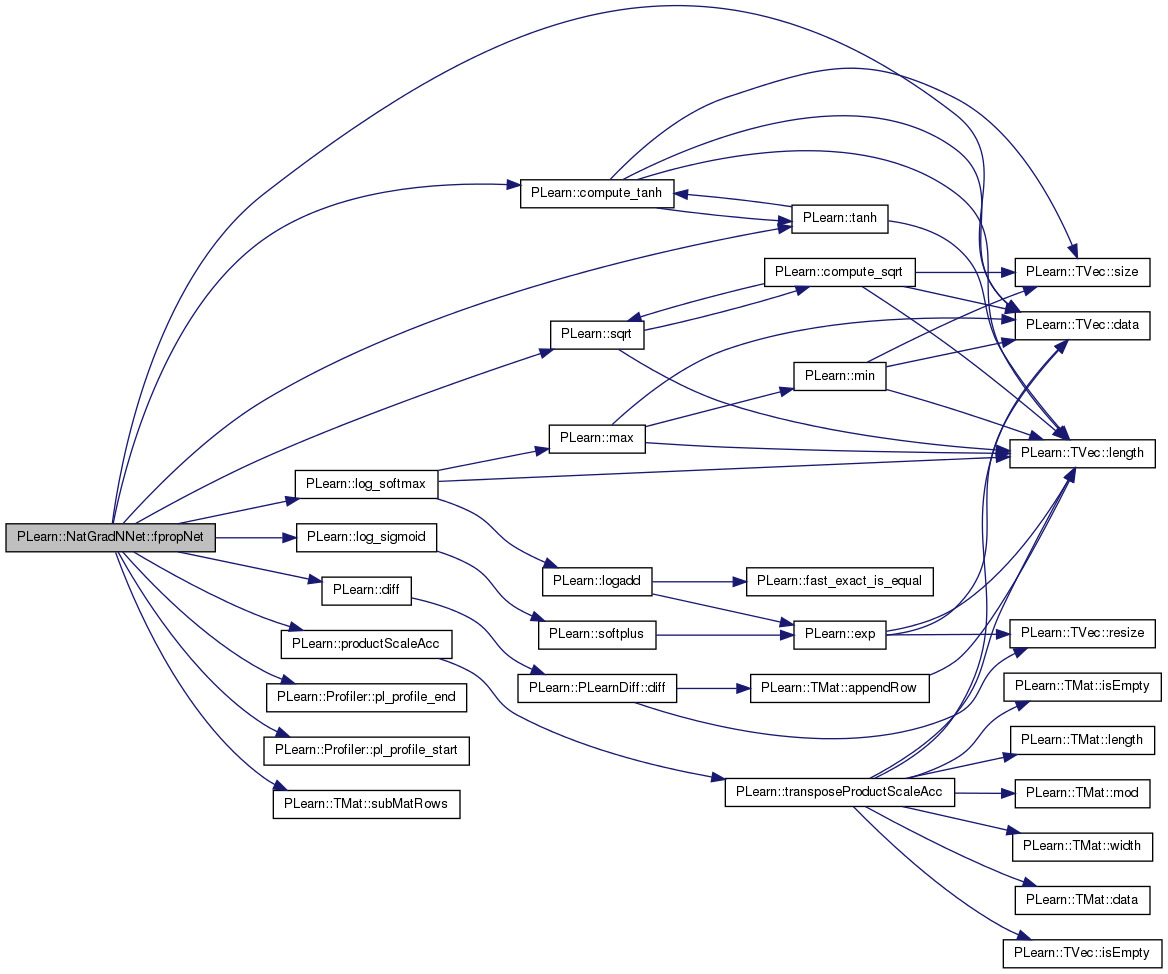
compute a minibatch of size n_examples network top-layer output given layer 0 output (= network input) (note that log-probabilities are computed for classification tasks, output_type=NLL)
compute (pre-final-non-linearity) network top-layer output given input
Definition at line 840 of file NatGradNNet.cc.
References a, activation_statistics_moving_average_coefficient, activations_scaling, b, biases, PLearn::compute_tanh(), PLearn::TVec< T >::data(), PLearn::diff(), i, j, layer_mparams, layer_params, layer_sizes, PLearn::log_sigmoid(), PLearn::log_softmax(), m, mean_activations, minibatch_size, mweights, PLearn::PLearner::n_examples, n_layers, neuron_extended_outputs_per_layer, neuron_outputs_per_layer, output_type, params_averaging_coeff, params_natgrad_per_input_template, PLearn::Profiler::pl_profile_end(), PLearn::Profiler::pl_profile_start(), PLASSERT_MSG, PLearn::productScaleAcc(), self_adjusted_scaling_and_bias, PLearn::sqrt(), PLearn::TMat< T >::subMatRows(), PLearn::tanh(), target_mean_activation, target_stdev_activation, var_activations, w, and weights.
Referenced by computeOutput(), computeOutputs(), and onlineStep().
{
PLASSERT_MSG(n_examples<=minibatch_size,"NatGradNNet::fpropNet: nb input vectors treated should be <= minibatch_size\n");
for (int i=0;i<n_layers-1;i++)
{
Mat prev_layer = (self_adjusted_scaling_and_bias && i+1<n_layers-1)?
neuron_outputs_per_layer[i]:neuron_extended_outputs_per_layer[i];
Mat next_layer = neuron_outputs_per_layer[i+1];
if (n_examples!=minibatch_size)
{
prev_layer = prev_layer.subMatRows(0,n_examples);
next_layer = next_layer.subMatRows(0,n_examples);
}
//alternate
// Are the input weights transposed? (because of ...)
bool tw = true;
if( params_natgrad_per_input_template && i==0 )
tw = false;
// try to use BLAS for the expensive operation
if (self_adjusted_scaling_and_bias && i+1<n_layers-1){
if (during_training)
Profiler::pl_profile_start("ProducScaleAccFpropTrain");
else
Profiler::pl_profile_start("ProducScaleAccFpropNoTrain");
productScaleAcc(next_layer, prev_layer, false,
(during_training || params_averaging_coeff==1.0)?
weights[i]:mweights[i],
tw, 1, 0);
if (during_training)
Profiler::pl_profile_end("ProducScaleAccFpropTrain");
else
Profiler::pl_profile_end("ProducScaleAcccFpropNoTrain");
}else{
if (during_training)
Profiler::pl_profile_start("ProducScaleAccFpropTrain");
else
Profiler::pl_profile_start("ProducScaleAcccFpropNoTrain");
productScaleAcc(next_layer, prev_layer, false,
(during_training || params_averaging_coeff==1.0)?
layer_params[i]:layer_mparams[i],
tw, 1, 0);
if (during_training)
Profiler::pl_profile_end("ProducScaleAccFpropTrain");
else
Profiler::pl_profile_end("ProducScaleAcccFpropNoTrain");
}
// compute layer's output non-linearity
if (i+1<n_layers-1)
for (int k=0;k<n_examples;k++)
{
Vec L=next_layer(k);
if (self_adjusted_scaling_and_bias)
{
real* m=mean_activations[i].data();
real* v=var_activations[i].data();
real* a=L.data();
real* s=activations_scaling[i].data();
real* b=biases[i].data(); // biases[i] is a 1-column matrix
int bmod = biases[i].mod();
for (int j=0;j<layer_sizes[i+1];j++,b+=bmod,m++,v++,a++,s++)
{
if (during_training)
{
real diff = *a - *m;
*v = (1-activation_statistics_moving_average_coefficient) * *v
+ activation_statistics_moving_average_coefficient * diff*diff;
*m = (1-activation_statistics_moving_average_coefficient) * *m
+ activation_statistics_moving_average_coefficient * *a;
*b = target_mean_activation - *m;
if (*v<100*target_stdev_activation*target_stdev_activation)
*s = target_stdev_activation/sqrt(*v);
else // rescale the weights and the statistics for that neuron
{
real rescale_factor = target_stdev_activation/sqrt(*v);
Vec w = weights[i](j);
w *= rescale_factor;
*b *= rescale_factor;
*s = 1;
*m *= rescale_factor;
*v *= rescale_factor*rescale_factor;
}
}
Profiler::pl_profile_start("activation function");
*a = tanh((*a + *b) * *s);
Profiler::pl_profile_end("activation function");
}
}
else{
Profiler::pl_profile_start("activation function");
compute_tanh(L,L);
Profiler::pl_profile_end("activation function");
}
}
else if (output_type=="NLL")
for (int k=0;k<n_examples;k++)
{
Vec L=next_layer(k);
Profiler::pl_profile_start("activation function");
log_softmax(L,L);
Profiler::pl_profile_end("activation function");
}
else if (output_type=="cross_entropy") {
for (int k=0;k<n_examples;k++)
{
Vec L=next_layer(k);
Profiler::pl_profile_start("activation function");
log_sigmoid(L,L);
Profiler::pl_profile_end("activation function");
}
}
}
}

| OptionList & PLearn::NatGradNNet::getOptionList | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 56 of file NatGradNNet.cc.
| OptionMap & PLearn::NatGradNNet::getOptionMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 56 of file NatGradNNet.cc.
| RemoteMethodMap & PLearn::NatGradNNet::getRemoteMethodMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 56 of file NatGradNNet.cc.
| TVec< string > PLearn::NatGradNNet::getTestCostNames | ( | ) | const [virtual] |
Returns the names of the costs computed by computeCostsFromOutpus (and thus the test method).
Implements PLearn::PLearner.
Definition at line 1074 of file NatGradNNet.cc.
References output_type, and PLearn::TVec< T >::resize().
Referenced by getTrainCostNames().
{
TVec<string> costs;
if (output_type=="NLL")
{
costs.resize(3);
costs[0]="NLL";
costs[1]="class_error";
costs[2]="weighted_class_error";
}
else if (output_type=="cross_entropy") {
costs.resize(3);
costs[0]="cross_entropy";
costs[1]="class_error";
costs[2]="weighted_class_error";
}
else if (output_type=="MSE")
{
costs.resize(1);
costs[0]="MSE";
}
return costs;
}


| TVec< string > PLearn::NatGradNNet::getTrainCostNames | ( | ) | const [virtual] |
Returns the names of the objective costs that the train method computes and for which it updates the VecStatsCollector train_stats.
Implements PLearn::PLearner.
Definition at line 1098 of file NatGradNNet.cc.
References PLearn::TVec< T >::append(), and getTestCostNames().
Referenced by build_().
{
TVec<string> costs = getTestCostNames();
costs.append("train_seconds");
costs.append("cum_train_seconds");
return costs;
}


| void PLearn::NatGradNNet::makeDeepCopyFromShallowCopy | ( | CopiesMap & | copies | ) | [virtual] |
Transforms a shallow copy into a deep copy.
Reimplemented from PLearn::PLearner.
Definition at line 464 of file NatGradNNet.cc.
References activations_scaling, all_mparams, all_params, all_params_delta, all_params_gradient, biases, PLearn::deepCopyField(), example_weights, full_natgrad, group_params, group_params_delta, group_params_gradient, hidden_layer_sizes, layer_mparams, layer_params, layer_params_delta, layer_params_gradient, layer_sizes, PLearn::PLearner::makeDeepCopyFromShallowCopy(), mweights, neuron_extended_outputs_per_layer, neuron_gradients, neuron_gradients_per_layer, neuron_outputs_per_layer, neurons_natgrad_per_layer, neurons_natgrad_template, params_natgrad_per_group, params_natgrad_per_input_template, params_natgrad_template, targets, train_costs, and weights.
{
inherited::makeDeepCopyFromShallowCopy(copies);
deepCopyField(hidden_layer_sizes, copies);
deepCopyField(layer_params, copies);
deepCopyField(layer_mparams, copies);
deepCopyField(biases, copies);
deepCopyField(weights, copies);
deepCopyField(mweights, copies);
deepCopyField(activations_scaling, copies);
deepCopyField(neurons_natgrad_template, copies);
deepCopyField(neurons_natgrad_per_layer, copies);
deepCopyField(params_natgrad_template, copies);
deepCopyField(params_natgrad_per_input_template, copies);
deepCopyField(params_natgrad_per_group, copies);
deepCopyField(full_natgrad, copies);
deepCopyField(layer_sizes, copies);
deepCopyField(targets, copies);
deepCopyField(example_weights, copies);
deepCopyField(train_costs, copies);
deepCopyField(neuron_outputs_per_layer, copies);
deepCopyField(neuron_extended_outputs_per_layer, copies);
deepCopyField(all_params, copies);
deepCopyField(all_mparams, copies);
deepCopyField(all_params_gradient, copies);
deepCopyField(layer_params_gradient, copies);
deepCopyField(neuron_gradients, copies);
deepCopyField(neuron_gradients_per_layer, copies);
deepCopyField(all_params_delta, copies);
deepCopyField(group_params, copies);
deepCopyField(group_params_gradient, copies);
deepCopyField(group_params_delta, copies);
deepCopyField(layer_params_delta, copies);
/*
deepCopyField(, copies);
*/
}

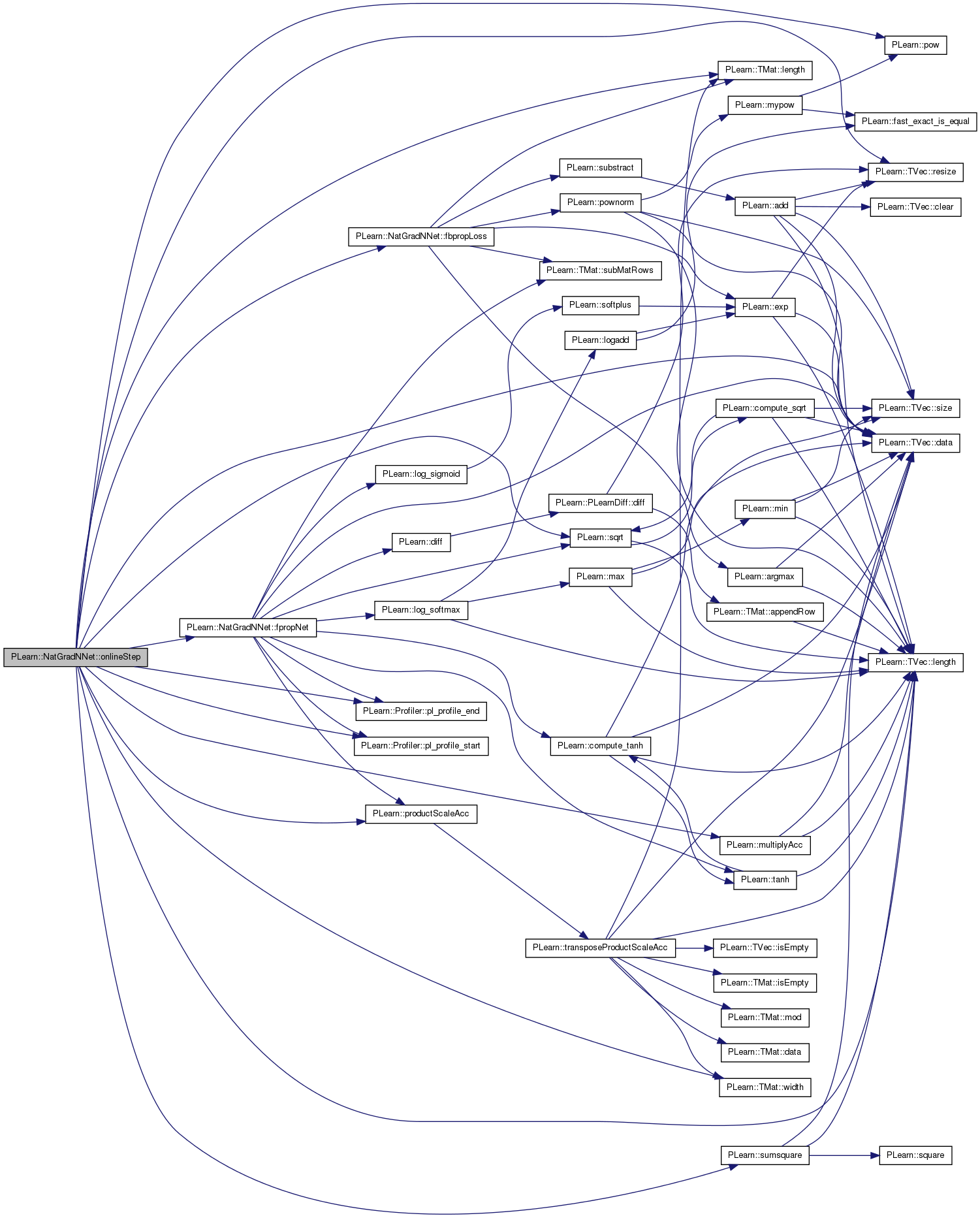
| void PLearn::NatGradNNet::onlineStep | ( | int | t, |
| const Mat & | targets, | ||
| Mat & | train_costs, | ||
| Vec | example_weights | ||
| ) | [protected] |
one minibatch training step
Definition at line 653 of file NatGradNNet.cc.
References activations_scaling, all_params, all_params_delta, all_params_gradient, PLearn::TVec< T >::data(), fbpropLoss(), fpropNet(), full_natgrad, g, grad, group_params_delta, group_params_gradient, i, init_lrate, input_size_lrate_normalization_power, j, layer_params, layer_params_delta, layer_params_gradient, layer_sizes, PLearn::TMat< T >::length(), PLearn::TVec< T >::length(), lrate_decay, minibatch_size, PLearn::multiplyAcc(), n_layers, neuron_extended_outputs_per_layer, neuron_gradients_per_layer, neuron_outputs_per_layer, neurons_natgrad_per_layer, neurons_natgrad_template, output_layer_L1_penalty_factor, output_layer_lrate_scale, params_natgrad_per_group, params_natgrad_per_input_template, params_natgrad_template, PLearn::Profiler::pl_profile_end(), PLearn::Profiler::pl_profile_start(), PLASSERT, PLearn::pow(), PLearn::productScaleAcc(), PLearn::TVec< T >::resize(), self_adjusted_scaling_and_bias, PLearn::sqrt(), PLearn::sumsquare(), weights, and PLearn::TMat< T >::width().
Referenced by train().
{
// mean gradient over minibatch_size examples has less variance, can afford larger learning rate
real lrate = sqrt(real(minibatch_size))*init_lrate/(1 + t*lrate_decay);
PLASSERT(targets.length()==minibatch_size && train_costs.length()==minibatch_size && example_weights.length()==minibatch_size);
fpropNet(minibatch_size,true);
fbpropLoss(neuron_outputs_per_layer[n_layers-1],targets,example_weights,train_costs);
for (int i=n_layers-1;i>0;i--)
{
// here neuron_gradients_per_layer[i] contains the gradient on activations (weighted sums)
// (minibatch_size x layer_size[i])
Mat previous_neurons_gradient = neuron_gradients_per_layer[i-1];
Mat next_neurons_gradient = neuron_gradients_per_layer[i];
Mat previous_neurons_output = neuron_outputs_per_layer[i-1];
real layer_lrate_factor = (i==n_layers-1)?output_layer_lrate_scale:1;
if (self_adjusted_scaling_and_bias && i+1<n_layers-1)
for (int k=0;k<minibatch_size;k++)
{
Vec g=next_neurons_gradient(k);
g*=activations_scaling[i-1]; // pass gradient through scaling
}
if (input_size_lrate_normalization_power==-1)
layer_lrate_factor /= sumsquare(neuron_extended_outputs_per_layer[i-1]);
else if (input_size_lrate_normalization_power==-2)
layer_lrate_factor /= sqrt(sumsquare(neuron_extended_outputs_per_layer[i-1]));
else if (input_size_lrate_normalization_power!=0)
{
int fan_in = neuron_extended_outputs_per_layer[i-1].length();
if (input_size_lrate_normalization_power==1)
layer_lrate_factor/=fan_in;
else if (input_size_lrate_normalization_power==2)
layer_lrate_factor/=sqrt(real(fan_in));
else layer_lrate_factor/=pow(fan_in,1.0/input_size_lrate_normalization_power);
}
// optionally correct the gradient on neurons using their covariance
if (neurons_natgrad_template && neurons_natgrad_per_layer[i])
{
static Vec tmp;
tmp.resize(layer_sizes[i]);
for (int k=0;k<minibatch_size;k++)
{
Vec g_k = next_neurons_gradient(k);
(*neurons_natgrad_per_layer[i])(t-minibatch_size+1+k,g_k,tmp);
g_k << tmp;
}
}
if (i>1) // compute gradient on previous layer
{
// propagate gradients
Profiler::pl_profile_start("ProducScaleAccOnlineStep");
productScaleAcc(previous_neurons_gradient,next_neurons_gradient,false,
weights[i-1],false,1,0);
Profiler::pl_profile_end("ProducScaleAccOnlineStep");
// propagate through tanh non-linearity
for (int j=0;j<previous_neurons_gradient.length();j++)
{
real* grad = previous_neurons_gradient[j];
real* out = previous_neurons_output[j];
for (int k=0;k<previous_neurons_gradient.width();k++,out++)
grad[k] *= (1 - *out * *out); // gradient through tanh derivative
}
}
// compute gradient on parameters, possibly update them
if (full_natgrad || params_natgrad_template || params_natgrad_per_input_template)
{
//alternate
if( params_natgrad_per_input_template && i==1 ){ // parameters are transposed
Profiler::pl_profile_start("ProducScaleAccOnlineStep");
productScaleAcc(layer_params_gradient[i-1],
neuron_extended_outputs_per_layer[i-1], true,
next_neurons_gradient, false,
1, 0);
Profiler::pl_profile_end("ProducScaleAccOnlineStep");
}else{
Profiler::pl_profile_start("ProducScaleAccOnlineStep");
productScaleAcc(layer_params_gradient[i-1],next_neurons_gradient,true,
neuron_extended_outputs_per_layer[i-1],false,1,0);
Profiler::pl_profile_end("ProducScaleAccOnlineStep");
}
layer_params_gradient[i-1] *= 1.0/minibatch_size; // use the MEAN gradient
} else {// just regular stochastic gradient
// compute gradient on weights and update them in one go (more efficient)
// mean gradient has less variance, can afford larger learning rate
Profiler::pl_profile_start("ProducScaleAccOnlineStep");
productScaleAcc(layer_params[i-1],next_neurons_gradient,true,
neuron_extended_outputs_per_layer[i-1],false,
-layer_lrate_factor*lrate/minibatch_size,1);
Profiler::pl_profile_end("ProducScaleAccOnlineStep");
// Don't do the stochastic trick - remember the gradient times its
// learning rate
/*productScaleAcc(layer_params_gradient[i-1],next_neurons_gradient,true,
neuron_extended_outputs_per_layer[i-1],false,
-layer_lrate_factor*lrate/minibatch_size,0);
layer_params[i-1] += layer_params_gradient[i-1];*/
// *stat* - compute and store the gradient
/*productScaleAcc(layer_params_gradient[i-1],next_neurons_gradient,true,
neuron_extended_outputs_per_layer[i-1],false,
1,0);*/
}
}
if (full_natgrad)
{
(*full_natgrad)(t/minibatch_size,all_params_gradient,all_params_delta); // compute update direction by natural gradient
if (output_layer_lrate_scale!=1.0)
layer_params_delta[n_layers-2] *= output_layer_lrate_scale; // scale output layer's learning rate
multiplyAcc(all_params,all_params_delta,-lrate); // update
// Hack to apply batch gradient even in this case (used for profiling
// the gradient correlations)
//if (output_layer_lrate_scale!=1.0)
// layer_params_gradient[n_layers-2] *= output_layer_lrate_scale; // scale output layer's learning rate
// multiplyAcc(all_params,all_params_gradient,-lrate); // update
} else if (params_natgrad_template || params_natgrad_per_input_template)
{
for (int i=0;i<params_natgrad_per_group.length();i++)
{
GradientCorrector& neuron_natgrad = *(params_natgrad_per_group[i]);
neuron_natgrad(t/minibatch_size,group_params_gradient[i],group_params_delta[i]); // compute update direction by natural gradient
}
//alternate
if (output_layer_lrate_scale!=1.0)
layer_params_delta[n_layers-2] *= output_layer_lrate_scale; // scale output layer's learning rate
multiplyAcc(all_params,all_params_delta,-lrate); // update
}
// Output layer L1 regularization
if( output_layer_L1_penalty_factor != 0. ) {
real L1_delta = lrate * output_layer_L1_penalty_factor;
real* m_i = layer_params[n_layers-2].data();
for(int i=0; i<layer_params[n_layers-2].length(); i++,m_i+=layer_params[n_layers-2].mod()) {
for(int j=0; j<layer_params[n_layers-2].width(); j++) {
if( m_i[j] > L1_delta )
m_i[j] -= L1_delta;
else if( m_i[j] < -L1_delta )
m_i[j] += L1_delta;
else
m_i[j] = 0.;
}
}
}
// profiling gradient correlation
//if( (t>=corr_profiling_start) && (t<=corr_profiling_end) && g_corrprof ) {
// (*g_corrprof)(all_params_gradient);
// (*ng_corrprof)(all_params_delta);
//}
// temporary - Need some stats for pvgrad analysis
// SGrad stats. This includes the learning rate.
/*if( ! use_pvgrad ) {
sum_gradient_norms += norm(all_params_gradient,2.0);
all_params_cum_gradient += all_params_gradient;
}*/
// Ouput for profiling: weights
// horribly inefficient! Anyway the Mat output is done one number at a
// time...
// do it locally, say on /part/01/Tmp
/* ofstream fd_params;
fd_params.open("params.txt", ios::app);
fd_params << layer_params[0](0) << " " << layer_params[1](0) << endl;
fd_params.close();
ofstream fd_gradients;
fd_gradients.open("gradients.txt", ios::app);
//fd_gradients << all_params_gradient << endl;
fd_gradients << layer_params_gradient[0](0) << " " <<layer_params_gradient[1](0) << endl;
fd_gradients.close();
*/
}

| int PLearn::NatGradNNet::outputsize | ( | ) | const [virtual] |
Returns the size of this learner's output, (which typically may depend on its inputsize(), targetsize() and set options).
Implements PLearn::PLearner.
Definition at line 505 of file NatGradNNet.cc.
References noutputs.
Referenced by computeOutputsAndCosts().
{
return noutputs;
}

| void PLearn::NatGradNNet::train | ( | ) | [virtual] |
The role of the train method is to bring the learner up to stage==nstages, updating the train_stats collector with training costs measured on-line in the process.
Implements PLearn::PLearner.
Definition at line 544 of file NatGradNNet.cc.
References all_mparams, all_params, b, build(), classname(), cumulative_training_time, PLearn::Profiler::end(), example_weights, PLearn::TVec< T >::fill(), PLearn::TMat< T >::fill(), PLearn::VMat::getExample(), PLearn::Profiler::getStats(), i, PLearn::PLearner::inputsize_, PLearn::VMat::length(), minibatch_size, MISSING_VALUE, PLearn::multiplyScaledAdd(), neuron_outputs_per_layer, PLearn::PLearner::nstages, onlineStep(), params_averaging_coeff, params_averaging_freq, PLearn::Profiler::pl_profile_end(), PLearn::Profiler::pl_profile_start(), PLERROR, PLearn::Profiler::report(), PLearn::PLearner::report_progress, PLearn::Profiler::reset(), PLearn::TMat< T >::resize(), PLearn::sample(), PLearn::PLearner::setTrainStatsCollector(), PLearn::PLearner::stage, PLearn::Profiler::start(), PLearn::TVec< T >::subVec(), PLearn::Profiler::Stats::system_duration, targets, PLearn::PLearner::targetsize(), PLearn::Profiler::ticksPerSecond(), train_costs, PLearn::PLearner::train_set, PLearn::PLearner::train_stats, PLearn::Profiler::Stats::user_duration, PLearn::PLearner::verbosity, and PLearn::TMat< T >::width().
{
if (inputsize_<0)
build();
targets.resize(minibatch_size,targetsize()); // the train_set's targetsize()
if(!train_set)
PLERROR("In NNet::train, you did not setTrainingSet");
if(!train_stats)
setTrainStatsCollector(new VecStatsCollector());
train_costs.fill(MISSING_VALUE) ;
train_stats->forget();
PP<ProgressBar> pb;
Profiler::reset("training");
Profiler::start("training");
Profiler::pl_profile_start("Totaltraining");
if( report_progress && stage < nstages )
pb = new ProgressBar( "Training "+classname(),
nstages - stage );
int start_stage=stage;
Vec costs_plus_time(train_costs.width()+2);
costs_plus_time[train_costs.width()] = MISSING_VALUE;
costs_plus_time[train_costs.width()+1] = MISSING_VALUE;
Vec costs = costs_plus_time.subVec(0,train_costs.width());
int nsamples = train_set->length();
// *stat* - Need some stats for grad analysis
//sum_gradient_norms = 0.0;
//all_params_cum_gradient.fill(0.0);
for( ; stage<nstages; stage++)
{
int sample = stage % nsamples;
int b = stage % minibatch_size;
Vec input = neuron_outputs_per_layer[0](b);
Vec target = targets(b);
Profiler::pl_profile_start("NatGradNNet::getting_data");
train_set->getExample(sample, input, target, example_weights[b]);
Profiler::pl_profile_end("NatGradNNet::getting_data");
if (b+1==minibatch_size) // do also special end-case || stage+1==nstages)
{
onlineStep(stage, targets, train_costs, example_weights );
for (int i=0;i<minibatch_size;i++)
{
costs << train_costs(b);
train_stats->update( costs_plus_time );
}
}
if (params_averaging_coeff!=1.0 &&
b==minibatch_size-1 &&
(stage+1)%(minibatch_size*params_averaging_freq)==0)
multiplyScaledAdd(all_params, 1-params_averaging_coeff,
params_averaging_coeff, all_mparams);
if( pb )
pb->update( stage + 1 - start_stage);
// *stat*
//(pa_gradstats[(int)targets(0,0)]).update( all_params_gradient );
}
Profiler::end("training");
Profiler::pl_profile_end("Totaltraining");
if (verbosity>0)
Profiler::report(cout);
const Profiler::Stats& stats = Profiler::getStats("training");
costs.fill(MISSING_VALUE);
real ticksPerSec = Profiler::ticksPerSecond();
real cpu_time = (stats.user_duration+stats.system_duration)/ticksPerSec;
cumulative_training_time += cpu_time;
costs_plus_time[train_costs.width()] = cpu_time;
costs_plus_time[train_costs.width()+1] = cumulative_training_time;
train_stats->update( costs_plus_time );
train_stats->finalize(); // finalize statistics for this epoch
// *stat*
// profiling gradient correlation
//if( g_corrprof ) {
// PLASSERT( corr_profiling_end <= nstages );
// g_corrprof->printAndReset();
// ng_corrprof->printAndReset();
//}
// *stat* - Need some stats for grad analysis
// The SGrad stats include the learning rate.
//cout << "sum_gradient_norms " << sum_gradient_norms
// << " norm(all_params_cum_gradient,2.0) " << norm(all_params_cum_gradient,2.0) << endl;
// *stat*
//for(int i=0; i<noutputs; i++) {
// ofstream fd_cov;
// stringstream ss;
// ss << "cov" << i+1 << ".txt";
// fd_cov.open(ss.str().c_str());
// fd_cov << (pa_gradstats[i]).getCovariance();
// fd_cov.close();
//}
}
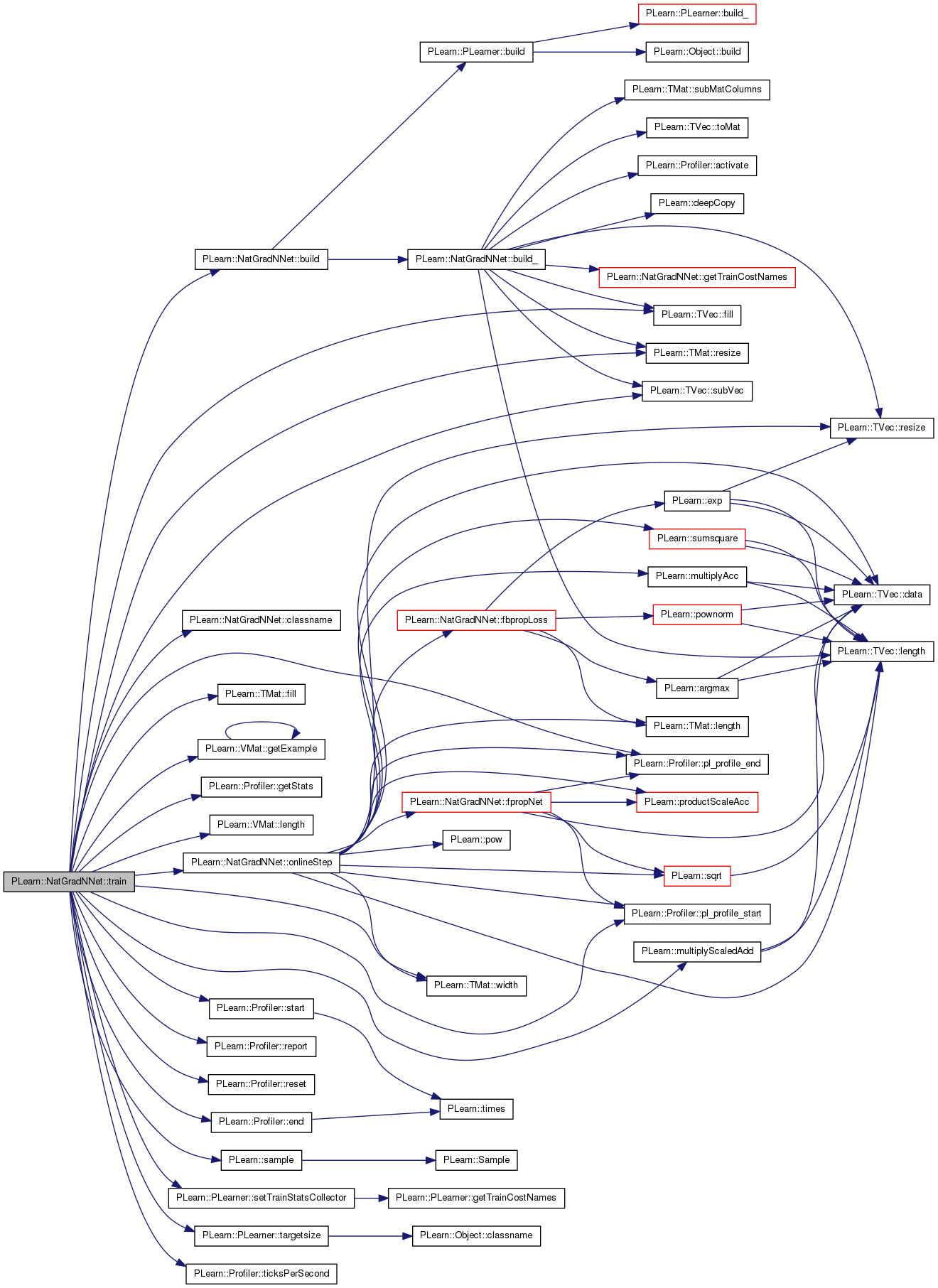
Reimplemented from PLearn::PLearner.
Definition at line 235 of file NatGradNNet.h.
Definition at line 141 of file NatGradNNet.h.
Referenced by declareOptions(), and fpropNet().
TVec<Vec> PLearn::NatGradNNet::activations_scaling [protected] |
Definition at line 258 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), forget(), fpropNet(), makeDeepCopyFromShallowCopy(), and onlineStep().
Vec PLearn::NatGradNNet::all_mparams [private] |
Definition at line 297 of file NatGradNNet.h.
Referenced by build_(), forget(), makeDeepCopyFromShallowCopy(), and train().
Vec PLearn::NatGradNNet::all_params [private] |
Definition at line 294 of file NatGradNNet.h.
Referenced by build_(), forget(), makeDeepCopyFromShallowCopy(), onlineStep(), and train().
Vec PLearn::NatGradNNet::all_params_delta [private] |
Definition at line 295 of file NatGradNNet.h.
Referenced by build_(), makeDeepCopyFromShallowCopy(), and onlineStep().
Vec PLearn::NatGradNNet::all_params_gradient [private] |
Definition at line 296 of file NatGradNNet.h.
Referenced by build_(), makeDeepCopyFromShallowCopy(), and onlineStep().
TVec<Mat> PLearn::NatGradNNet::biases [protected] |
pointers into the layer_params
Definition at line 256 of file NatGradNNet.h.
Referenced by build_(), forget(), fpropNet(), and makeDeepCopyFromShallowCopy().
real PLearn::NatGradNNet::cumulative_training_time [protected] |
Definition at line 261 of file NatGradNNet.h.
Referenced by declareOptions(), forget(), and train().
Vec PLearn::NatGradNNet::example_weights [private] |
Definition at line 308 of file NatGradNNet.h.
Referenced by build_(), makeDeepCopyFromShallowCopy(), and train().
optionally, if neurons_natgrad==0 and params_natgrad_template==0, one can have regular stochastic gradient descent, or full-covariance natural gradient using the natural gradient estimator below
Definition at line 114 of file NatGradNNet.h.
Referenced by declareOptions(), makeDeepCopyFromShallowCopy(), and onlineStep().
TVec<Vec> PLearn::NatGradNNet::group_params [private] |
Definition at line 300 of file NatGradNNet.h.
Referenced by build_(), and makeDeepCopyFromShallowCopy().
TVec<Vec> PLearn::NatGradNNet::group_params_delta [private] |
Definition at line 301 of file NatGradNNet.h.
Referenced by build_(), makeDeepCopyFromShallowCopy(), and onlineStep().
TVec<Vec> PLearn::NatGradNNet::group_params_gradient [private] |
Definition at line 302 of file NatGradNNet.h.
Referenced by build_(), makeDeepCopyFromShallowCopy(), and onlineStep().
sizes of hidden layers, provided by the user.
Definition at line 63 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), and makeDeepCopyFromShallowCopy().
initial learning rate
Definition at line 77 of file NatGradNNet.h.
Referenced by declareOptions(), and onlineStep().
0 does not scale the learning rate 1 scales it by 1 / the nb of inputs of the neuron 2 scales it by 1 / sqrt(the nb of inputs of the neuron) etc.
Definition at line 123 of file NatGradNNet.h.
Referenced by declareOptions(), and onlineStep().
mean layer_params, averaged over past updates (moving average)
Definition at line 69 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), fpropNet(), and makeDeepCopyFromShallowCopy().
layer_params[i] is a matrix of dimension layer_sizes[i+1] x (layer_sizes[i]+1) containing the neuron biases in its first column.
Definition at line 67 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), fpropNet(), makeDeepCopyFromShallowCopy(), and onlineStep().
TVec<Vec> PLearn::NatGradNNet::layer_params_delta [private] |
Definition at line 299 of file NatGradNNet.h.
Referenced by build_(), makeDeepCopyFromShallowCopy(), and onlineStep().
TVec<Mat> PLearn::NatGradNNet::layer_params_gradient [private] |
Definition at line 298 of file NatGradNNet.h.
Referenced by build_(), makeDeepCopyFromShallowCopy(), and onlineStep().
TVec<int> PLearn::NatGradNNet::layer_sizes [protected] |
layer sizes (derived from hidden_layer_sizes, inputsize_ and outputsize_)
Definition at line 253 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), forget(), fpropNet(), makeDeepCopyFromShallowCopy(), and onlineStep().
learning rate decay factor
Definition at line 80 of file NatGradNNet.h.
Referenced by declareOptions(), and onlineStep().
scale the learning rate in different neurons by a factor taken randomly as follows: choose integer n uniformly between lrate_scale_factor_min_power and lrate_scale_factor_max_power inclusively, and then scale learning rate by lrate_scale_factor^n.
Definition at line 129 of file NatGradNNet.h.
Referenced by declareOptions().
Definition at line 130 of file NatGradNNet.h.
Referenced by declareOptions().
Definition at line 131 of file NatGradNNet.h.
Referenced by declareOptions().
TVec<Vec> PLearn::NatGradNNet::mean_activations [protected] |
Definition at line 259 of file NatGradNNet.h.
Referenced by build_(), forget(), and fpropNet().
update the parameters only so often
Definition at line 89 of file NatGradNNet.h.
Referenced by build_(), computeOutputs(), declareOptions(), fbpropLoss(), fpropNet(), onlineStep(), and train().
TVec<Mat> PLearn::NatGradNNet::mweights [protected] |
Definition at line 257 of file NatGradNNet.h.
Referenced by build_(), fpropNet(), and makeDeepCopyFromShallowCopy().
int PLearn::NatGradNNet::n_layers [protected] |
number of layers of weights (2 for a neural net with one hidden layer)
Definition at line 250 of file NatGradNNet.h.
Referenced by build_(), computeOutput(), computeOutputs(), declareOptions(), fbpropLoss(), forget(), fpropNet(), and onlineStep().
TVec<Mat> PLearn::NatGradNNet::neuron_extended_outputs_per_layer [mutable, private] |
Definition at line 306 of file NatGradNNet.h.
Referenced by build_(), fpropNet(), makeDeepCopyFromShallowCopy(), and onlineStep().
Mat PLearn::NatGradNNet::neuron_gradients [private] |
Definition at line 303 of file NatGradNNet.h.
Referenced by build_(), and makeDeepCopyFromShallowCopy().
Definition at line 304 of file NatGradNNet.h.
Referenced by build_(), fbpropLoss(), makeDeepCopyFromShallowCopy(), and onlineStep().
TVec<Mat> PLearn::NatGradNNet::neuron_outputs_per_layer [mutable, private] |
Definition at line 305 of file NatGradNNet.h.
Referenced by build_(), computeOutput(), computeOutputs(), fpropNet(), makeDeepCopyFromShallowCopy(), onlineStep(), and train().
Definition at line 94 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), makeDeepCopyFromShallowCopy(), and onlineStep().
natural gradient estimator for neurons (if 0 then do not correct the gradient on neurons)
Definition at line 93 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), makeDeepCopyFromShallowCopy(), and onlineStep().
Definition at line 60 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), fbpropLoss(), and outputsize().
L1 penalty applied to the output layer's parameters.
Definition at line 83 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), and onlineStep().
scaling factor of the learning rate for the output layer
Definition at line 86 of file NatGradNNet.h.
Referenced by declareOptions(), and onlineStep().
type of output cost: "NLL" for classification problems, "MSE" for regression
Definition at line 117 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), fbpropLoss(), fpropNet(), and getTestCostNames().
mparams <-- (1-params_averaging_coeff)mparams + params_averaging_coeff*params
Definition at line 72 of file NatGradNNet.h.
Referenced by declareOptions(), forget(), fpropNet(), and train().
how often (in terms of minibatches, i.e. weight updates) do we perform the above?
Definition at line 74 of file NatGradNNet.h.
Referenced by declareOptions(), and train().
the above templates are used by the user to specifiy all the elements of the vector below
Definition at line 109 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), makeDeepCopyFromShallowCopy(), and onlineStep().
natural gradient estimator solely for the parameters of the first layer.
If present, performs over groups of parameters related to the same input (this includes the additional bias input). Has precedence over params_natgrad_template, ie if present, there is no natural gradient performed on the groups of a neuron's parameters: params_natgrad_template is not applied for the first hidden layer's parameters).
Definition at line 106 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), fpropNet(), makeDeepCopyFromShallowCopy(), and onlineStep().
natural gradient estimator for the parameters within each neuron (if 0 then do not correct the gradient on each neuron weight)
Definition at line 98 of file NatGradNNet.h.
Referenced by build_(), declareOptions(), makeDeepCopyFromShallowCopy(), and onlineStep().
Let each neuron self-adjust its bias and scaling factor of its activations so that the mean and standard deviation of the activations reach the target_mean_activation and target_stdev_activation.
Definition at line 136 of file NatGradNNet.h.
Referenced by declareOptions(), fpropNet(), and onlineStep().
Definition at line 137 of file NatGradNNet.h.
Referenced by declareOptions(), and fpropNet().
Definition at line 138 of file NatGradNNet.h.
Referenced by declareOptions(), and fpropNet().
Mat PLearn::NatGradNNet::targets [private] |
Definition at line 307 of file NatGradNNet.h.
Referenced by makeDeepCopyFromShallowCopy(), and train().
Mat PLearn::NatGradNNet::train_costs [private] |
Definition at line 309 of file NatGradNNet.h.
Referenced by build_(), makeDeepCopyFromShallowCopy(), and train().
TVec<Vec> PLearn::NatGradNNet::var_activations [protected] |
Definition at line 260 of file NatGradNNet.h.
Referenced by build_(), forget(), and fpropNet().
TVec<Mat> PLearn::NatGradNNet::weights [protected] |
Definition at line 257 of file NatGradNNet.h.
Referenced by build_(), forget(), fpropNet(), makeDeepCopyFromShallowCopy(), and onlineStep().
 1.7.4
1.7.4