|
PLearn 0.1
|
|
PLearn 0.1
|
Multi-layer neural network based on matrix-matrix multiplications. More...
#include <PvGradNNet.h>
Public Member Functions | |
| PvGradNNet () | |
| virtual void | forget () |
| (Re-)initializes the PLearner in its fresh state (that state may depend on the 'seed' option) and sets 'stage' back to 0 (this is the stage of a fresh learner!). | |
| virtual string | classname () const |
| virtual OptionList & | getOptionList () const |
| virtual OptionMap & | getOptionMap () const |
| virtual RemoteMethodMap & | getRemoteMethodMap () const |
| virtual PvGradNNet * | deepCopy (CopiesMap &copies) const |
| virtual void | build () |
| Finish building the object; just call inherited::build followed by build_() | |
| virtual void | makeDeepCopyFromShallowCopy (CopiesMap &copies) |
| Transforms a shallow copy into a deep copy. | |
Static Public Member Functions | |
| static string | _classname_ () |
| static OptionList & | _getOptionList_ () |
| static RemoteMethodMap & | _getRemoteMethodMap_ () |
| static Object * | _new_instance_for_typemap_ () |
| static bool | _isa_ (const Object *o) |
| static void | _static_initialize_ () |
| static const PPath & | declaringFile () |
Public Attributes | |
| real | pv_initial_stepsize |
| Initial size of steps in parameter space. | |
| real | pv_min_stepsize |
| Bounds for the step sizes. | |
| real | pv_max_stepsize |
| real | pv_acceleration |
| Coefficients by which to multiply the step sizes. | |
| real | pv_deceleration |
| int | pv_min_samples |
| PV's gradient minimum number of samples to estimate confidence. | |
| real | pv_required_confidence |
| Minimum required confidence (probability of being positive or negative) for taking a step. | |
| real | pv_conf_ct |
| int | pv_strategy |
| bool | pv_random_sample_step |
| If this is set to true, then we will randomly choose the step sign for. | |
| real | pv_self_discount |
| For the discounting strategy. | |
| real | pv_other_discount |
| real | pv_within_neuron_discount |
Static Public Attributes | |
| static StaticInitializer | _static_initializer_ |
Protected Member Functions | |
| virtual void | bpropUpdateNet (const int t) |
| Performs the backprop update. Must be called after the fbpropNet. | |
| void | pvGrad () |
| void | discountGrad () |
| This gradient strategy is much like the one from PvGrad, however: | |
| void | neuronDiscountGrad () |
| Same as discountGrad but also performs discount based on within neuron relationships. | |
| void | globalSyncGrad () |
| void | neuronSyncGrad () |
Static Protected Member Functions | |
| static void | declareOptions (OptionList &ol) |
| Declares the class options. | |
Private Types | |
| typedef mNNet | inherited |
Private Member Functions | |
| void | build_ () |
| This does the actual building. | |
Private Attributes | |
| Vec | pv_all_nsamples |
| Holds the number of samples gathered for each weight. | |
| TVec< Mat > | pv_layer_nsamples |
| Vec | pv_all_sum |
| Sum of collected gradients. | |
| TVec< Mat > | pv_layer_sum |
| Vec | pv_all_sumsquare |
| Sum of squares of collected gradients. | |
| TVec< Mat > | pv_layer_sumsquare |
| TVec< int > | pv_all_stepsigns |
| Temporary add-on. Allows an undetermined signed value (zero). | |
| TVec< TMat< int > > | pv_layer_stepsigns |
| Vec | pv_all_stepsizes |
| The step size (absolute value) to be taken for each parameter. | |
| TVec< Mat > | pv_layer_stepsizes |
| int | n_updates |
| Number of weight updates performed during a call to bpropUpdateNet. | |
| TVec< int > | n_neuron_updates |
| real | limit_ratio |
| accumulated statistics of gradients on each parameter. | |
| real | n_small_ratios |
Multi-layer neural network based on matrix-matrix multiplications.
Definition at line 49 of file PvGradNNet.h.
typedef mNNet PLearn::PvGradNNet::inherited [private] |
Reimplemented from PLearn::mNNet.
Definition at line 51 of file PvGradNNet.h.
| PLearn::PvGradNNet::PvGradNNet | ( | ) |
Definition at line 51 of file PvGradNNet.cc.
References PLearn::PLearner::random_gen.
: mNNet(), pv_initial_stepsize(1e-1), pv_min_stepsize(1e-6), pv_max_stepsize(50.0), pv_acceleration(1.2), pv_deceleration(0.5), pv_min_samples(2), pv_required_confidence(0.80), pv_conf_ct(0.0), pv_strategy(1), pv_random_sample_step(false), pv_self_discount(0.5), pv_other_discount(0.95), pv_within_neuron_discount(0.95), n_updates(0), limit_ratio(0.0), n_small_ratios(0.0) { random_gen = new PRandom(); }
| string PLearn::PvGradNNet::_classname_ | ( | ) | [static] |
Reimplemented from PLearn::mNNet.
Definition at line 49 of file PvGradNNet.cc.
| OptionList & PLearn::PvGradNNet::_getOptionList_ | ( | ) | [static] |
Reimplemented from PLearn::mNNet.
Definition at line 49 of file PvGradNNet.cc.
| RemoteMethodMap & PLearn::PvGradNNet::_getRemoteMethodMap_ | ( | ) | [static] |
Reimplemented from PLearn::mNNet.
Definition at line 49 of file PvGradNNet.cc.
Reimplemented from PLearn::mNNet.
Definition at line 49 of file PvGradNNet.cc.
| Object * PLearn::PvGradNNet::_new_instance_for_typemap_ | ( | ) | [static] |
Reimplemented from PLearn::mNNet.
Definition at line 49 of file PvGradNNet.cc.
| StaticInitializer PvGradNNet::_static_initializer_ & PLearn::PvGradNNet::_static_initialize_ | ( | ) | [static] |
Reimplemented from PLearn::mNNet.
Definition at line 49 of file PvGradNNet.cc.
| void PLearn::PvGradNNet::bpropUpdateNet | ( | const int | t | ) | [protected, virtual] |
Performs the backprop update. Must be called after the fbpropNet.
Reimplemented from PLearn::mNNet.
Definition at line 231 of file PvGradNNet.cc.
References PLearn::mNNet::bpropNet(), discountGrad(), PLearn::endl(), globalSyncGrad(), n_small_ratios, neuronDiscountGrad(), neuronSyncGrad(), PLERROR, pv_strategy, and pvGrad().
{
bpropNet(t);
switch( pv_strategy ) {
case 1 :
pvGrad();
break;
case 2 :
discountGrad();
break;
case 3 :
neuronDiscountGrad();
break;
case 4 :
globalSyncGrad();
break;
case 5 :
neuronSyncGrad();
break;
default :
PLERROR("PvGradNNet::bpropUpdateNet() - No such pv_strategy.");
}
// hack
if( (t%160000)==0 ) {
cout << n_small_ratios << " small ratios." << endl;
n_small_ratios = 0.0;
}
}
| void PLearn::PvGradNNet::build | ( | ) | [virtual] |
Finish building the object; just call inherited::build followed by build_()
Reimplemented from PLearn::mNNet.
Definition at line 183 of file PvGradNNet.cc.
References PLearn::mNNet::build(), and build_().
{
inherited::build();
build_();
}
| void PLearn::PvGradNNet::build_ | ( | ) | [private] |
This does the actual building.
Reimplemented from PLearn::mNNet.
Definition at line 151 of file PvGradNNet.cc.
References PLearn::mNNet::all_params, i, PLearn::mNNet::layer_sizes, PLearn::TVec< T >::length(), n, PLearn::mNNet::n_layers, n_neuron_updates, pv_all_nsamples, pv_all_stepsigns, pv_all_stepsizes, pv_all_sum, pv_all_sumsquare, pv_layer_nsamples, pv_layer_stepsigns, pv_layer_stepsizes, pv_layer_sum, pv_layer_sumsquare, PLearn::TVec< T >::resize(), PLearn::TVec< T >::subVec(), and PLearn::TVec< T >::toMat().
Referenced by build().
{
int n = all_params.length();
pv_all_nsamples.resize(n);
pv_all_sum.resize(n);
pv_all_sumsquare.resize(n);
pv_all_stepsigns.resize(n);
pv_all_stepsizes.resize(n);
// Get some structure on the previous Vecs
pv_layer_nsamples.resize(n_layers-1);
pv_layer_sum.resize(n_layers-1);
pv_layer_sumsquare.resize(n_layers-1);
pv_layer_stepsigns.resize(n_layers-1);
pv_layer_stepsizes.resize(n_layers-1);
int np;
int n_neurons=0;
for (int i=0,p=0;i<n_layers-1;i++) {
np=layer_sizes[i+1]*(1+layer_sizes[i]);
pv_layer_nsamples.subVec(p,np).toMat(layer_sizes[i+1],layer_sizes[i]+1);
pv_layer_sum.subVec(p,np).toMat(layer_sizes[i+1],layer_sizes[i]+1);
pv_layer_sumsquare.subVec(p,np).toMat(layer_sizes[i+1],layer_sizes[i]+1);
pv_layer_stepsigns[i]=pv_all_stepsigns.subVec(p,np).toMat(layer_sizes[i+1],layer_sizes[i]+1);
pv_layer_stepsizes[i]=pv_all_stepsizes.subVec(p,np).toMat(layer_sizes[i+1],layer_sizes[i]+1);
p+=np;
n_neurons+=layer_sizes[i+1];
}
n_neuron_updates.resize(n_neurons);
}

| string PLearn::PvGradNNet::classname | ( | ) | const [virtual] |
Reimplemented from PLearn::mNNet.
Definition at line 49 of file PvGradNNet.cc.
| void PLearn::PvGradNNet::declareOptions | ( | OptionList & | ol | ) | [static, protected] |
Declares the class options.
Reimplemented from PLearn::mNNet.
Definition at line 73 of file PvGradNNet.cc.
References PLearn::OptionBase::buildoption, PLearn::declareOption(), PLearn::mNNet::declareOptions(), pv_acceleration, pv_conf_ct, pv_deceleration, pv_initial_stepsize, pv_max_stepsize, pv_min_samples, pv_min_stepsize, pv_other_discount, pv_random_sample_step, pv_required_confidence, pv_self_discount, pv_strategy, and pv_within_neuron_discount.
{
declareOption(ol, "pv_initial_stepsize",
&PvGradNNet::pv_initial_stepsize,
OptionBase::buildoption,
"Initial size of steps in parameter space");
declareOption(ol, "pv_min_stepsize",
&PvGradNNet::pv_min_stepsize,
OptionBase::buildoption,
"Minimal size of steps in parameter space");
declareOption(ol, "pv_max_stepsize",
&PvGradNNet::pv_max_stepsize,
OptionBase::buildoption,
"Maximal size of steps in parameter space");
declareOption(ol, "pv_acceleration",
&PvGradNNet::pv_acceleration,
OptionBase::buildoption,
"Coefficient by which to multiply the step sizes.");
declareOption(ol, "pv_deceleration",
&PvGradNNet::pv_deceleration,
OptionBase::buildoption,
"Coefficient by which to multiply the step sizes.");
declareOption(ol, "pv_min_samples",
&PvGradNNet::pv_min_samples,
OptionBase::buildoption,
"PV's minimum number of samples to estimate gradient sign.\n"
"This should at least be 2.");
declareOption(ol, "pv_required_confidence",
&PvGradNNet::pv_required_confidence,
OptionBase::buildoption,
"Minimum required confidence (probability of being positive or negative) for taking a step.");
declareOption(ol, "pv_conf_ct",
&PvGradNNet::pv_conf_ct,
OptionBase::buildoption,
"Used for confidence adaptation.");
declareOption(ol, "pv_strategy",
&PvGradNNet::pv_strategy,
OptionBase::buildoption,
"Strategy to use for the weight updates (number from 1 to 4).");
declareOption(ol, "pv_random_sample_step",
&PvGradNNet::pv_random_sample_step,
OptionBase::buildoption,
"If this is set to true, then we will randomly choose the step sign\n"
"for each parameter based on the estimated probability of it being\n"
"positive or negative.");
declareOption(ol, "pv_self_discount",
&PvGradNNet::pv_self_discount,
OptionBase::buildoption,
"Discount used to perform soft invalidation of a weight's statistics\n"
"after its update.");
declareOption(ol, "pv_other_discount",
&PvGradNNet::pv_other_discount,
OptionBase::buildoption,
"Discount used to perform soft invalidation of other weights'\n"
"statistics after a weight update.");
declareOption(ol, "pv_within_neuron_discount",
&PvGradNNet::pv_within_neuron_discount,
OptionBase::buildoption,
"Discount used to perform soft invalidation of other weights'\n"
"(same neuron) statistics after a weight update.");
// Now call the parent class' declareOptions
inherited::declareOptions(ol);
}

| static const PPath& PLearn::PvGradNNet::declaringFile | ( | ) | [inline, static] |
Reimplemented from PLearn::mNNet.
Definition at line 104 of file PvGradNNet.h.
:
//##### Protected Options ###############################################
| PvGradNNet * PLearn::PvGradNNet::deepCopy | ( | CopiesMap & | copies | ) | const [virtual] |
Reimplemented from PLearn::mNNet.
Definition at line 49 of file PvGradNNet.cc.
| void PLearn::PvGradNNet::discountGrad | ( | ) | [protected] |
This gradient strategy is much like the one from PvGrad, however:
Definition at line 372 of file PvGradNNet.cc.
References PLearn::mNNet::all_params, PLearn::mNNet::all_params_gradient, PLearn::gauss_01_quantile(), PLearn::TVec< T >::length(), limit_ratio, m, n_small_ratios, n_updates, PLWARNING, PLearn::pow(), pv_acceleration, pv_all_nsamples, pv_all_stepsigns, pv_all_stepsizes, pv_all_sum, pv_all_sumsquare, pv_conf_ct, pv_deceleration, pv_max_stepsize, pv_min_samples, pv_min_stepsize, pv_other_discount, pv_required_confidence, pv_self_discount, PLearn::sqrt(), PLearn::square(), and PLearn::PLearner::stage.
Referenced by bpropUpdateNet().
{
int np = all_params.length();
real m, e;//, prob_pos, prob_neg;
int stepsign;
// TODO bring the confidenca treatment up to date (see pvGrad)
real ratio;
real conf = pv_required_confidence;
if( pv_conf_ct != 0.0 ) {
conf += (1.0-pv_required_confidence) * (stage/stage+pv_conf_ct);
}
real limit_ratio = gauss_01_quantile(conf);
//
real discount = pow(pv_other_discount,n_updates);
n_updates = 0;
if( discount < 0.001 )
PLWARNING("PvGradNNet::discountGrad() - discount < 0.001 - that seems small...");
real sd = pv_self_discount / pv_other_discount; // trick: apply this self discount
// and then discount
// everyone the same
for(int k=0; k<np; k++) {
// Perform soft invalidation
pv_all_nsamples[k] *= discount;
pv_all_sum[k] *= discount;
pv_all_sumsquare[k] *= discount;
// update stats
pv_all_nsamples[k]++;
pv_all_sum[k] += all_params_gradient[k];
pv_all_sumsquare[k] += all_params_gradient[k] * all_params_gradient[k];
if(pv_all_nsamples[k]>pv_min_samples) {
m = pv_all_sum[k] / pv_all_nsamples[k];
e = real((pv_all_sumsquare[k] - square(pv_all_sum[k])/pv_all_nsamples[k])/(pv_all_nsamples[k]-1));
e = sqrt(e/pv_all_nsamples[k]);
// test to see if numerical problems
if( fabs(m) < 1e-15 || e < 1e-15 ) {
//cout << "PvGradNNet::bpropUpdateNet() - small mean-error ratio." << endl;
n_small_ratios++;
continue;
}
// TODO - for current treatment, not necessary to compute actual
// prob. Comparing the ratio would be sufficient.
/*prob_pos = gauss_01_cum(m/e);
prob_neg = 1.-prob_pos;
if(prob_pos>=pv_required_confidence)
stepsign = 1;
else if(prob_neg>=pv_required_confidence)
stepsign = -1;
else
continue;*/
ratio=m/e;
if(ratio>=limit_ratio)
stepsign = 1;
else if(ratio<=-limit_ratio)
stepsign = -1;
else
continue;
// consecutive steps of same sign, accelerate
if( stepsign*pv_all_stepsigns[k]>0 ) {
pv_all_stepsizes[k]*=pv_acceleration;
if( pv_all_stepsizes[k] > pv_max_stepsize )
pv_all_stepsizes[k] = pv_max_stepsize;
// else if different signs decelerate
} else if( stepsign*pv_all_stepsigns[k]<0 ) {
pv_all_stepsizes[k]*=pv_deceleration;
if( pv_all_stepsizes[k] < pv_min_stepsize )
pv_all_stepsizes[k] = pv_min_stepsize;
// else (previous sign was undetermined
}// else {
//}
// step
if( stepsign > 0 )
all_params[k] -= pv_all_stepsizes[k];
else
all_params[k] += pv_all_stepsizes[k];
pv_all_stepsigns[k] = stepsign;
// soft invalidation of self
pv_all_nsamples[k]*=sd;
pv_all_sum[k]*=sd;
pv_all_sumsquare[k]*=sd;
n_updates++;
}
}
}

| void PLearn::PvGradNNet::forget | ( | ) | [virtual] |
(Re-)initializes the PLearner in its fresh state (that state may depend on the 'seed' option) and sets 'stage' back to 0 (this is the stage of a fresh learner!).
(Re-)initialize the PLearner in its fresh state (that state may depend on the 'seed' option) and sets 'stage' back to 0 (this is the stage of a fresh learner!)
Reimplemented from PLearn::mNNet.
Definition at line 208 of file PvGradNNet.cc.
References PLearn::TVec< T >::fill(), PLearn::mNNet::forget(), PLearn::gauss_01_quantile(), limit_ratio, n_neuron_updates, n_small_ratios, n_updates, pv_all_nsamples, pv_all_stepsigns, pv_all_stepsizes, pv_all_sum, pv_all_sumsquare, pv_initial_stepsize, and pv_required_confidence.
{
inherited::forget();
pv_all_nsamples.fill(0);
pv_all_sum.fill(0.0);
pv_all_sumsquare.fill(0.0);
pv_all_stepsigns.fill(0);
pv_all_stepsizes.fill(pv_initial_stepsize);
// used in the discountGrad() strategy
n_updates = 0;
n_small_ratios=0.0;
n_neuron_updates.fill(0);
// pv_gradstats->forget();
limit_ratio = gauss_01_quantile(pv_required_confidence);
}
| OptionList & PLearn::PvGradNNet::getOptionList | ( | ) | const [virtual] |
Reimplemented from PLearn::mNNet.
Definition at line 49 of file PvGradNNet.cc.
| OptionMap & PLearn::PvGradNNet::getOptionMap | ( | ) | const [virtual] |
Reimplemented from PLearn::mNNet.
Definition at line 49 of file PvGradNNet.cc.
| RemoteMethodMap & PLearn::PvGradNNet::getRemoteMethodMap | ( | ) | const [virtual] |
Reimplemented from PLearn::mNNet.
Definition at line 49 of file PvGradNNet.cc.
| void PLearn::PvGradNNet::globalSyncGrad | ( | ) | [protected] |
Definition at line 559 of file PvGradNNet.cc.
Referenced by bpropUpdateNet().
{
}

| void PLearn::PvGradNNet::makeDeepCopyFromShallowCopy | ( | CopiesMap & | copies | ) | [virtual] |
Transforms a shallow copy into a deep copy.
Reimplemented from PLearn::mNNet.
Definition at line 190 of file PvGradNNet.cc.
References PLearn::deepCopyField(), PLearn::mNNet::makeDeepCopyFromShallowCopy(), n_neuron_updates, pv_all_nsamples, pv_all_stepsigns, pv_all_stepsizes, pv_all_sum, pv_all_sumsquare, pv_layer_nsamples, pv_layer_stepsigns, pv_layer_stepsizes, pv_layer_sum, and pv_layer_sumsquare.
{
inherited::makeDeepCopyFromShallowCopy(copies);
deepCopyField(pv_all_nsamples, copies);
deepCopyField(pv_layer_nsamples, copies);
deepCopyField(pv_all_sum, copies);
deepCopyField(pv_layer_sum, copies);
deepCopyField(pv_all_sumsquare, copies);
deepCopyField(pv_layer_sumsquare, copies);
deepCopyField(pv_all_stepsigns, copies);
deepCopyField(pv_layer_stepsigns, copies);
deepCopyField(pv_all_stepsizes, copies);
deepCopyField(pv_layer_stepsizes, copies);
deepCopyField(n_neuron_updates, copies);
// deepCopyField(pv_gradstats, copies);
}

| void PLearn::PvGradNNet::neuronDiscountGrad | ( | ) | [protected] |
Same as discountGrad but also performs discount based on within neuron relationships.
Definition at line 466 of file PvGradNNet.cc.
References PLearn::mNNet::all_params, PLearn::mNNet::all_params_gradient, d, PLearn::endl(), PLearn::gauss_01_quantile(), PLearn::mNNet::layer_sizes, limit_ratio, m, n, PLearn::mNNet::n_layers, n_neuron_updates, n_updates, PLWARNING, PLearn::pow(), pv_acceleration, pv_all_nsamples, pv_all_stepsigns, pv_all_stepsizes, pv_all_sum, pv_all_sumsquare, pv_conf_ct, pv_deceleration, pv_max_stepsize, pv_min_samples, pv_min_stepsize, pv_other_discount, pv_required_confidence, pv_self_discount, pv_within_neuron_discount, PLearn::sqrt(), PLearn::square(), PLearn::PLearner::stage, and w.
Referenced by bpropUpdateNet().
{
real m, e;//, prob_pos, prob_neg;
int stepsign;
// TODO bring the confidenca treatment up to date (see pvGrad)
real ratio;
real conf = pv_required_confidence;
if( pv_conf_ct != 0.0 ) {
conf += (1.0-pv_required_confidence) * (stage/stage+pv_conf_ct);
}
real limit_ratio = gauss_01_quantile(conf);
//
real discount = pow(pv_other_discount,n_updates);
real d;
n_updates = 0;
if( discount < 0.001 )
PLWARNING("PvGradNNet::discountGrad() - discount < 0.001 - that seems small...");
real sd = pv_self_discount / pv_other_discount; // trick: apply this self discount
// and then discount
// everyone the same
sd /= pv_within_neuron_discount;
// k is an index on all the parameters.
// kk is an index on all neurons.
for(int l=0,k=0,kk=0; l<n_layers-1; l++) {
for(int n=0; n<layer_sizes[l+1]; n++,kk++) {
d = discount * pow(pv_within_neuron_discount,n_neuron_updates[kk]);
n_neuron_updates[kk]=0;
for(int w=0; w<1+layer_sizes[l]; w++,k++) {
// Perform soft invalidation
pv_all_nsamples[k] *= d;
pv_all_sum[k] *= d;
pv_all_sumsquare[k] *= d;
// update stats
pv_all_nsamples[k]++;
pv_all_sum[k] += all_params_gradient[k];
pv_all_sumsquare[k] += all_params_gradient[k] * all_params_gradient[k];
if(pv_all_nsamples[k]>pv_min_samples) {
m = pv_all_sum[k] / pv_all_nsamples[k];
e = real((pv_all_sumsquare[k] - square(pv_all_sum[k])/pv_all_nsamples[k])/(pv_all_nsamples[k]-1));
e = sqrt(e/pv_all_nsamples[k]);
// test to see if numerical problems
if( fabs(m) < 1e-15 || e < 1e-15 ) {
cout << "PvGradNNet::bpropUpdateNet() - small mean-error ratio." << endl;
continue;
}
ratio=m/e;
if(ratio>=limit_ratio)
stepsign = 1;
else if(ratio<=-limit_ratio)
stepsign = -1;
else
continue;
// consecutive steps of same sign, accelerate
if( stepsign*pv_all_stepsigns[k]>0 ) {
pv_all_stepsizes[k]*=pv_acceleration;
if( pv_all_stepsizes[k] > pv_max_stepsize )
pv_all_stepsizes[k] = pv_max_stepsize;
// else if different signs decelerate
} else if( stepsign*pv_all_stepsigns[k]<0 ) {
pv_all_stepsizes[k]*=pv_deceleration;
if( pv_all_stepsizes[k] < pv_min_stepsize )
pv_all_stepsizes[k] = pv_min_stepsize;
// else (previous sign was undetermined
}// else {
//}
// step
if( stepsign > 0 )
all_params[k] -= pv_all_stepsizes[k];
else
all_params[k] += pv_all_stepsizes[k];
pv_all_stepsigns[k] = stepsign;
// soft invalidation of self
pv_all_nsamples[k]*=sd;
pv_all_sum[k]*=sd;
pv_all_sumsquare[k]*=sd;
n_updates++;
n_neuron_updates[kk]++;
}
}
}
}
}

| void PLearn::PvGradNNet::neuronSyncGrad | ( | ) | [protected] |
Definition at line 563 of file PvGradNNet.cc.
Referenced by bpropUpdateNet().
{
}

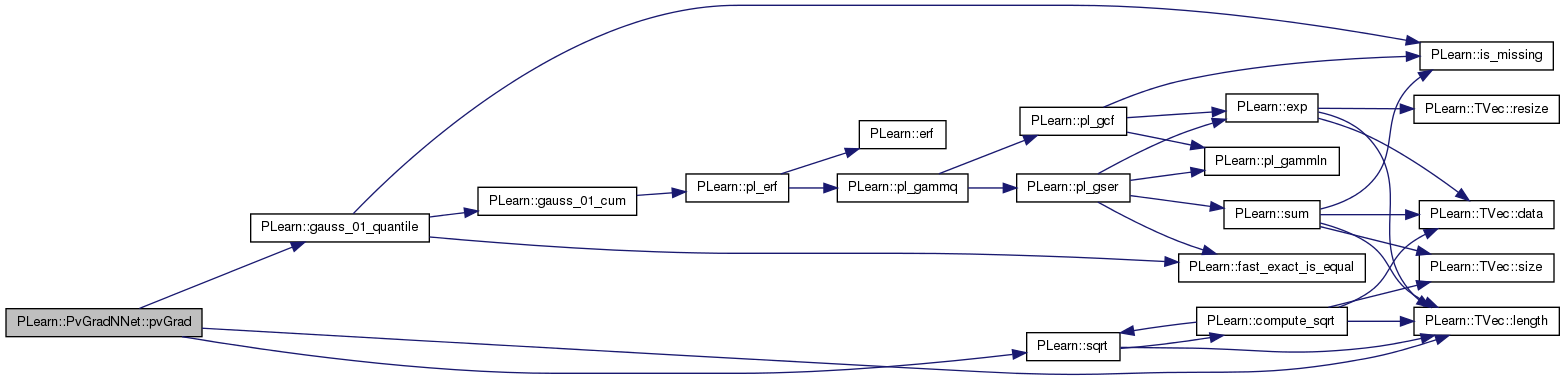
| void PLearn::PvGradNNet::pvGrad | ( | ) | [protected] |
Definition at line 262 of file PvGradNNet.cc.
References PLearn::mNNet::all_params, PLearn::mNNet::all_params_gradient, PLearn::gauss_01_quantile(), PLearn::TVec< T >::length(), limit_ratio, m, n_small_ratios, pv_acceleration, pv_all_nsamples, pv_all_stepsigns, pv_all_stepsizes, pv_all_sum, pv_all_sumsquare, pv_conf_ct, pv_deceleration, pv_max_stepsize, pv_min_samples, pv_min_stepsize, pv_random_sample_step, pv_required_confidence, PLearn::sqrt(), and PLearn::PLearner::stage.
Referenced by bpropUpdateNet().
{
int np = all_params.length();
real m, e;//, prob_pos, prob_neg;
//real ratio;
// move this stuff to a train function to avoid repeated computations
if( pv_conf_ct != 0.0 ) {
real conf = pv_required_confidence;
conf += (1.0-pv_required_confidence) * (stage/stage+pv_conf_ct);
limit_ratio = gauss_01_quantile(conf);
}
for(int k=0; k<np; k++) {
// update stats
pv_all_nsamples[k]++;
pv_all_sum[k] += all_params_gradient[k];
pv_all_sumsquare[k] += all_params_gradient[k] * all_params_gradient[k];
if(pv_all_nsamples[k]>pv_min_samples) {
real inv_pv_all_nsamples_k = 1./pv_all_nsamples[k];
real pv_all_sum_k = pv_all_sum[k];
m = pv_all_sum_k * inv_pv_all_nsamples_k;
// e is the standard error
// variance
//e = real((pv_all_sumsquare[k] - square(pv_all_sum[k])/pv_all_nsamples[k])/(pv_all_nsamples[k]-1));
// standard error
//e = sqrt(e*inv_pv_all_nsamples_k);
// This is an approxiamtion where we've raplaced a (nsamples-1) by nsamples
e = sqrt(pv_all_sumsquare[k]-pv_all_sum_k*m)*inv_pv_all_nsamples_k;
// test to see if numerical problems
if( fabs(m) < 1e-15 || e < 1e-15 ) {
//cout << "PvGradNNet::bpropUpdateNet() - small mean-error ratio." << endl;
n_small_ratios++;
continue;
}
// TODO - for current treatment, not necessary to compute actual prob.
// Comparing the ratio would be sufficient.
//prob_pos = gauss_01_cum(m/e);
//prob_neg = 1.-prob_pos;
//ratio = m/e;
if(!pv_random_sample_step) {
real threshold = limit_ratio*e;
// We adapt the stepsize before taking the step
// gradient is positive
//if(prob_pos>=pv_required_confidence) {
//if(ratio>=limit_ratio) {
if(m>=threshold) {
//pv_all_stepsizes[k] *= (pv_all_stepsigns[k]?pv_acceleration:pv_deceleration);
if(pv_all_stepsigns[k]>0) {
pv_all_stepsizes[k]*=pv_acceleration;
if( pv_all_stepsizes[k] > pv_max_stepsize )
pv_all_stepsizes[k] = pv_max_stepsize;
}
else if(pv_all_stepsigns[k]<0) {
pv_all_stepsizes[k]*=pv_deceleration;
if( pv_all_stepsizes[k] < pv_min_stepsize )
pv_all_stepsizes[k] = pv_min_stepsize;
}
all_params[k] -= pv_all_stepsizes[k];
pv_all_stepsigns[k] = 1;
pv_all_nsamples[k]=0;
pv_all_sum[k]=0.0;
pv_all_sumsquare[k]=0.0;
}
// gradient is negative
//else if(prob_neg>=pv_required_confidence) {
else if(m<=-threshold) {
//pv_all_stepsizes[k] *= ((!pv_all_stepsigns[k])?pv_acceleration:pv_deceleration);
if(pv_all_stepsigns[k]<0) {
pv_all_stepsizes[k]*=pv_acceleration;
if( pv_all_stepsizes[k] > pv_max_stepsize )
pv_all_stepsizes[k] = pv_max_stepsize;
}
else if(pv_all_stepsigns[k]>0) {
pv_all_stepsizes[k]*=pv_deceleration;
if( pv_all_stepsizes[k] < pv_min_stepsize )
pv_all_stepsizes[k] = pv_min_stepsize;
}
all_params[k] += pv_all_stepsizes[k];
pv_all_stepsigns[k] = -1;
pv_all_nsamples[k]=0;
pv_all_sum[k]=0.0;
pv_all_sumsquare[k]=0.0;
}
}
/*else // random sample update direction (sign)
{
bool ispos = (random_gen->binomial_sample(prob_pos)>0);
if(ispos) // picked positive
all_params[k] += pv_all_stepsizes[k];
else // picked negative
all_params[k] -= pv_all_stepsizes[k];
pv_all_stepsizes[k] *= (pv_all_stepsigns[k]==ispos)?pv_acceleration :pv_deceleration;
pv_all_stepsigns[k] = ispos;
st.forget();
}*/
}
//pv_all_nsamples[k] = ns; // *stat*
}
}

Reimplemented from PLearn::mNNet.
Definition at line 104 of file PvGradNNet.h.
real PLearn::PvGradNNet::limit_ratio [private] |
accumulated statistics of gradients on each parameter.
Definition at line 166 of file PvGradNNet.h.
Referenced by discountGrad(), forget(), neuronDiscountGrad(), and pvGrad().
TVec<int> PLearn::PvGradNNet::n_neuron_updates [private] |
Definition at line 161 of file PvGradNNet.h.
Referenced by build_(), forget(), makeDeepCopyFromShallowCopy(), and neuronDiscountGrad().
real PLearn::PvGradNNet::n_small_ratios [private] |
Definition at line 167 of file PvGradNNet.h.
Referenced by bpropUpdateNet(), discountGrad(), forget(), and pvGrad().
int PLearn::PvGradNNet::n_updates [private] |
Number of weight updates performed during a call to bpropUpdateNet.
Definition at line 159 of file PvGradNNet.h.
Referenced by discountGrad(), forget(), and neuronDiscountGrad().
Coefficients by which to multiply the step sizes.
Definition at line 63 of file PvGradNNet.h.
Referenced by declareOptions(), discountGrad(), neuronDiscountGrad(), and pvGrad().
Vec PLearn::PvGradNNet::pv_all_nsamples [private] |
Holds the number of samples gathered for each weight.
Definition at line 140 of file PvGradNNet.h.
Referenced by build_(), discountGrad(), forget(), makeDeepCopyFromShallowCopy(), neuronDiscountGrad(), and pvGrad().
TVec<int> PLearn::PvGradNNet::pv_all_stepsigns [private] |
Temporary add-on. Allows an undetermined signed value (zero).
Definition at line 150 of file PvGradNNet.h.
Referenced by build_(), discountGrad(), forget(), makeDeepCopyFromShallowCopy(), neuronDiscountGrad(), and pvGrad().
Vec PLearn::PvGradNNet::pv_all_stepsizes [private] |
The step size (absolute value) to be taken for each parameter.
Definition at line 154 of file PvGradNNet.h.
Referenced by build_(), discountGrad(), forget(), makeDeepCopyFromShallowCopy(), neuronDiscountGrad(), and pvGrad().
Vec PLearn::PvGradNNet::pv_all_sum [private] |
Sum of collected gradients.
Definition at line 143 of file PvGradNNet.h.
Referenced by build_(), discountGrad(), forget(), makeDeepCopyFromShallowCopy(), neuronDiscountGrad(), and pvGrad().
Vec PLearn::PvGradNNet::pv_all_sumsquare [private] |
Sum of squares of collected gradients.
Definition at line 146 of file PvGradNNet.h.
Referenced by build_(), discountGrad(), forget(), makeDeepCopyFromShallowCopy(), neuronDiscountGrad(), and pvGrad().
Definition at line 71 of file PvGradNNet.h.
Referenced by declareOptions(), discountGrad(), neuronDiscountGrad(), and pvGrad().
Definition at line 63 of file PvGradNNet.h.
Referenced by declareOptions(), discountGrad(), neuronDiscountGrad(), and pvGrad().
Initial size of steps in parameter space.
Definition at line 57 of file PvGradNNet.h.
Referenced by declareOptions(), and forget().
TVec< Mat > PLearn::PvGradNNet::pv_layer_nsamples [private] |
Definition at line 141 of file PvGradNNet.h.
Referenced by build_(), and makeDeepCopyFromShallowCopy().
TVec< TMat<int> > PLearn::PvGradNNet::pv_layer_stepsigns [private] |
Definition at line 151 of file PvGradNNet.h.
Referenced by build_(), and makeDeepCopyFromShallowCopy().
TVec<Mat> PLearn::PvGradNNet::pv_layer_stepsizes [private] |
Definition at line 155 of file PvGradNNet.h.
Referenced by build_(), and makeDeepCopyFromShallowCopy().
TVec<Mat> PLearn::PvGradNNet::pv_layer_sum [private] |
Definition at line 144 of file PvGradNNet.h.
Referenced by build_(), and makeDeepCopyFromShallowCopy().
TVec<Mat> PLearn::PvGradNNet::pv_layer_sumsquare [private] |
Definition at line 147 of file PvGradNNet.h.
Referenced by build_(), and makeDeepCopyFromShallowCopy().
Definition at line 60 of file PvGradNNet.h.
Referenced by declareOptions(), discountGrad(), neuronDiscountGrad(), and pvGrad().
PV's gradient minimum number of samples to estimate confidence.
Definition at line 66 of file PvGradNNet.h.
Referenced by declareOptions(), discountGrad(), neuronDiscountGrad(), and pvGrad().
Bounds for the step sizes.
Definition at line 60 of file PvGradNNet.h.
Referenced by declareOptions(), discountGrad(), neuronDiscountGrad(), and pvGrad().
Definition at line 82 of file PvGradNNet.h.
Referenced by declareOptions(), discountGrad(), and neuronDiscountGrad().
If this is set to true, then we will randomly choose the step sign for.
Definition at line 78 of file PvGradNNet.h.
Referenced by declareOptions(), and pvGrad().
Minimum required confidence (probability of being positive or negative) for taking a step.
Definition at line 70 of file PvGradNNet.h.
Referenced by declareOptions(), discountGrad(), forget(), neuronDiscountGrad(), and pvGrad().
For the discounting strategy.
Used to discount stats when there are updates
Definition at line 82 of file PvGradNNet.h.
Referenced by declareOptions(), discountGrad(), and neuronDiscountGrad().
Definition at line 73 of file PvGradNNet.h.
Referenced by bpropUpdateNet(), and declareOptions().
Definition at line 82 of file PvGradNNet.h.
Referenced by declareOptions(), and neuronDiscountGrad().
 1.7.4
1.7.4