|
PLearn 0.1
|
|
PLearn 0.1
|
returns exp(-norm_2(x1-x2)^2/sigma^2) More...
#include <GaussianKernel.h>
Public Member Functions | |
| GaussianKernel () | |
| Default constructor. | |
| GaussianKernel (real the_sigma) | |
| Convenient constructor. | |
| virtual string | classname () const |
| virtual OptionList & | getOptionList () const |
| virtual OptionMap & | getOptionMap () const |
| virtual RemoteMethodMap & | getRemoteMethodMap () const |
| virtual GaussianKernel * | deepCopy (CopiesMap &copies) const |
| virtual void | build () |
| Post-constructor. | |
| virtual void | makeDeepCopyFromShallowCopy (CopiesMap &copies) |
| Does the necessary operations to transform a shallow copy (this) into a deep copy by deep-copying all the members that need to be. | |
| virtual void | setDataForKernelMatrix (VMat the_data) |
| This method precomputes the squared norm for all the data to later speed up evaluate methods. | |
| virtual void | addDataForKernelMatrix (const Vec &newRow) |
| This method appends the newRow squared norm to the squarednorms Vec field. | |
| virtual real | evaluate (const Vec &x1, const Vec &x2) const |
| returns K(x1,x2) | |
| virtual real | evaluate_i_j (int i, int j) const |
| returns evaluate(data(i),data(j)) | |
| virtual real | evaluate_i_x (int i, const Vec &x, real squared_norm_of_x=-1) const |
| returns evaluate(data(i),x) | |
| virtual real | evaluate_x_i (const Vec &x, int i, real squared_norm_of_x=-1) const |
| returns evaluate(x,data(i)) | |
| virtual void | setParameters (Vec paramvec) |
| ** Subclasses may override these methods ** They provide a generic way to set and retrieve kernel parameters | |
Static Public Member Functions | |
| static string | _classname_ () |
| static OptionList & | _getOptionList_ () |
| static RemoteMethodMap & | _getRemoteMethodMap_ () |
| static Object * | _new_instance_for_typemap_ () |
| static bool | _isa_ (const Object *o) |
| static void | _static_initialize_ () |
| static const PPath & | declaringFile () |
Public Attributes | |
| bool | scale_by_sigma |
| Build options below. | |
| real | sigma |
Static Public Attributes | |
| static StaticInitializer | _static_initializer_ |
Protected Member Functions | |
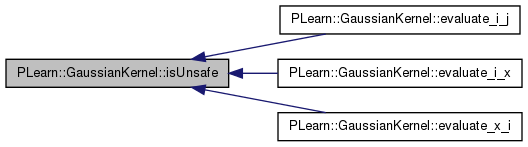
| bool | isUnsafe (real sqn_1, real sqn_2) const |
| Return true if estimating the squared difference of two points x1 and x2 from their squared norms sqn_1 and sqn_2 (and their dot product) might lead to unsafe numerical approximations. | |
Static Protected Member Functions | |
| static void | declareOptions (OptionList &ol) |
| Declare options (data fields) for the class. | |
Protected Attributes | |
| real | minus_one_over_sigmasquare |
| real | sigmasquare_over_two |
| sigma^2 / 2 | |
| Vec | squarednorms |
| squarednorms of the rows of the data VMat (data is a member of Kernel) | |
Private Types | |
| typedef Kernel | inherited |
Private Member Functions | |
| real | evaluateFromSquaredNormOfDifference (real sqnorm_of_diff) const |
| real | evaluateFromDotAndSquaredNorm (real sqnorm_x1, real dot_x1_x2, real sqnorm_x2) const |
| void | build_ () |
| Object-specific post-constructor. | |
returns exp(-norm_2(x1-x2)^2/sigma^2)
Definition at line 54 of file GaussianKernel.h.
typedef Kernel PLearn::GaussianKernel::inherited [private] |
Reimplemented from PLearn::Kernel.
Definition at line 59 of file GaussianKernel.h.
| PLearn::GaussianKernel::GaussianKernel | ( | ) |
Default constructor.
Definition at line 62 of file GaussianKernel.cc.
References build_().
: scale_by_sigma(false), sigma(1) { build_(); }

| PLearn::GaussianKernel::GaussianKernel | ( | real | the_sigma | ) |
Convenient constructor.
Definition at line 69 of file GaussianKernel.cc.
References build_().
: scale_by_sigma(false), sigma(the_sigma) { build_(); }

| string PLearn::GaussianKernel::_classname_ | ( | ) | [static] |
Reimplemented from PLearn::Kernel.
Definition at line 57 of file GaussianKernel.cc.
| OptionList & PLearn::GaussianKernel::_getOptionList_ | ( | ) | [static] |
Reimplemented from PLearn::Kernel.
Definition at line 57 of file GaussianKernel.cc.
| RemoteMethodMap & PLearn::GaussianKernel::_getRemoteMethodMap_ | ( | ) | [static] |
Reimplemented from PLearn::Kernel.
Definition at line 57 of file GaussianKernel.cc.
Reimplemented from PLearn::Kernel.
Definition at line 57 of file GaussianKernel.cc.
| Object * PLearn::GaussianKernel::_new_instance_for_typemap_ | ( | ) | [static] |
Reimplemented from PLearn::Object.
Definition at line 57 of file GaussianKernel.cc.
| StaticInitializer GaussianKernel::_static_initializer_ & PLearn::GaussianKernel::_static_initialize_ | ( | ) | [static] |
Reimplemented from PLearn::Kernel.
Definition at line 57 of file GaussianKernel.cc.
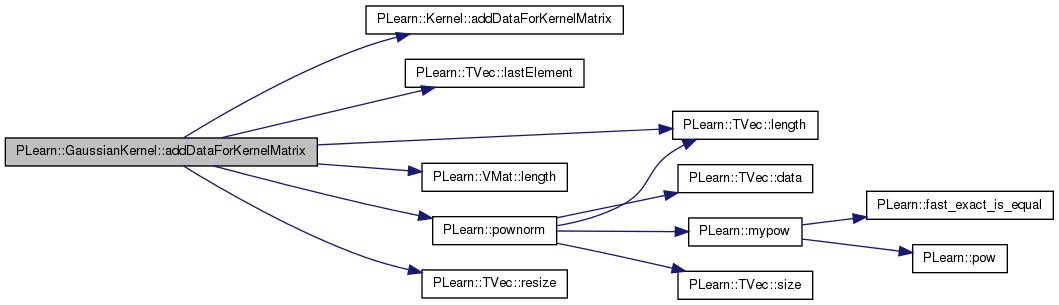
| void PLearn::GaussianKernel::addDataForKernelMatrix | ( | const Vec & | newRow | ) | [virtual] |
This method appends the newRow squared norm to the squarednorms Vec field.
Reimplemented from PLearn::Kernel.
Definition at line 116 of file GaussianKernel.cc.
References PLearn::Kernel::addDataForKernelMatrix(), PLearn::Kernel::data, PLearn::TVec< T >::lastElement(), PLearn::TVec< T >::length(), PLearn::VMat::length(), PLERROR, PLearn::pownorm(), PLearn::TVec< T >::resize(), and squarednorms.
{
inherited::addDataForKernelMatrix(newRow);
int dlen = data.length();
int sqlen = squarednorms.length();
if(sqlen == dlen-1)
squarednorms.resize(dlen);
else if(sqlen == dlen)
for(int s=1; s < sqlen; s++)
squarednorms[s-1] = squarednorms[s];
else
PLERROR("Only two scenarios are managed:\n"
"Either the data matrix was only appended the new row or, under the windowed settings,\n"
"newRow is the new last row and other rows were moved backward.\n"
"However, sqlen = %d and dlen = %d excludes both!", sqlen, dlen);
squarednorms.lastElement() = pownorm(newRow, 2);
}
| void PLearn::GaussianKernel::build | ( | ) | [virtual] |
Post-constructor.
The normal implementation should call simply inherited::build(), then this class's build_(). This method should be callable again at later times, after modifying some option fields to change the "architecture" of the object.
Reimplemented from PLearn::Kernel.
Definition at line 93 of file GaussianKernel.cc.
References PLearn::Kernel::build(), and build_().
{
inherited::build();
build_();
}

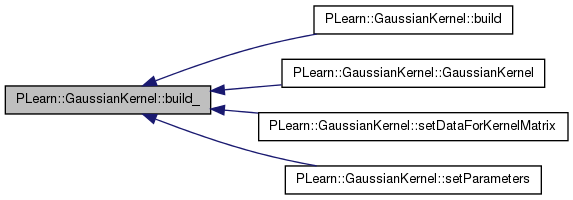
| void PLearn::GaussianKernel::build_ | ( | ) | [private] |
Object-specific post-constructor.
This method should be redefined in subclasses and do the actual building of the object according to previously set option fields. Constructors can just set option fields, and then call build_. This method is NOT virtual, and will typically be called only from three places: a constructor, the public virtual build() method, and possibly the public virtual read method (which calls its parent's read). build_() can assume that its parent's build_() has already been called.
Reimplemented from PLearn::Kernel.
Definition at line 102 of file GaussianKernel.cc.
References minus_one_over_sigmasquare, sigma, sigmasquare_over_two, and PLearn::square().
Referenced by build(), GaussianKernel(), setDataForKernelMatrix(), and setParameters().
{
minus_one_over_sigmasquare = -1.0/square(sigma);
sigmasquare_over_two = square(sigma) / 2.0;
}

| string PLearn::GaussianKernel::classname | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 57 of file GaussianKernel.cc.
| void PLearn::GaussianKernel::declareOptions | ( | OptionList & | ol | ) | [static, protected] |
Declare options (data fields) for the class.
Redefine this in subclasses: call declareOption(...) for each option, and then call inherited::declareOptions(options). Please call the inherited method AT THE END to get the options listed in a consistent order (from most recently defined to least recently defined).
static void MyDerivedClass::declareOptions(OptionList& ol) { declareOption(ol, "inputsize", &MyObject::inputsize_, OptionBase::buildoption, "The size of the input; it must be provided"); declareOption(ol, "weights", &MyObject::weights, OptionBase::learntoption, "The learned model weights"); inherited::declareOptions(ol); }
| ol | List of options that is progressively being constructed for the current class. |
Reimplemented from PLearn::Kernel.
Definition at line 79 of file GaussianKernel.cc.
References PLearn::OptionBase::buildoption, PLearn::declareOption(), PLearn::Kernel::declareOptions(), scale_by_sigma, and sigma.
{
declareOption(ol, "sigma", &GaussianKernel::sigma, OptionBase::buildoption,
"The width of the Gaussian.");
declareOption(ol, "scale_by_sigma", &GaussianKernel::scale_by_sigma, OptionBase::buildoption,
"If set to 1, the kernel will be scaled by sigma^2 / 2");
inherited::declareOptions(ol);
}

| static const PPath& PLearn::GaussianKernel::declaringFile | ( | ) | [inline, static] |
Reimplemented from PLearn::Kernel.
Definition at line 82 of file GaussianKernel.h.
:
static void declareOptions(OptionList& ol);
| GaussianKernel * PLearn::GaussianKernel::deepCopy | ( | CopiesMap & | copies | ) | const [virtual] |
Reimplemented from PLearn::Kernel.
Definition at line 57 of file GaussianKernel.cc.
returns K(x1,x2)
Implements PLearn::Kernel.
Definition at line 172 of file GaussianKernel.cc.
References PLearn::TVec< T >::data(), evaluateFromSquaredNormOfDifference(), i, PLearn::TVec< T >::length(), and PLERROR.
Referenced by PLearn::LocalizedFeaturesLayerVariable::computeSubsets().
{
#ifdef BOUNDCHECK
if(x1.length()!=x2.length())
PLERROR("IN GaussianKernel::evaluate x1 and x2 must have the same length");
#endif
int l = x1.length();
real* px1 = x1.data();
real* px2 = x2.data();
real sqnorm_of_diff = 0.;
for(int i=0; i<l; i++)
{
real val = px1[i]-px2[i];
sqnorm_of_diff += val*val;
}
return evaluateFromSquaredNormOfDifference(sqnorm_of_diff);
}


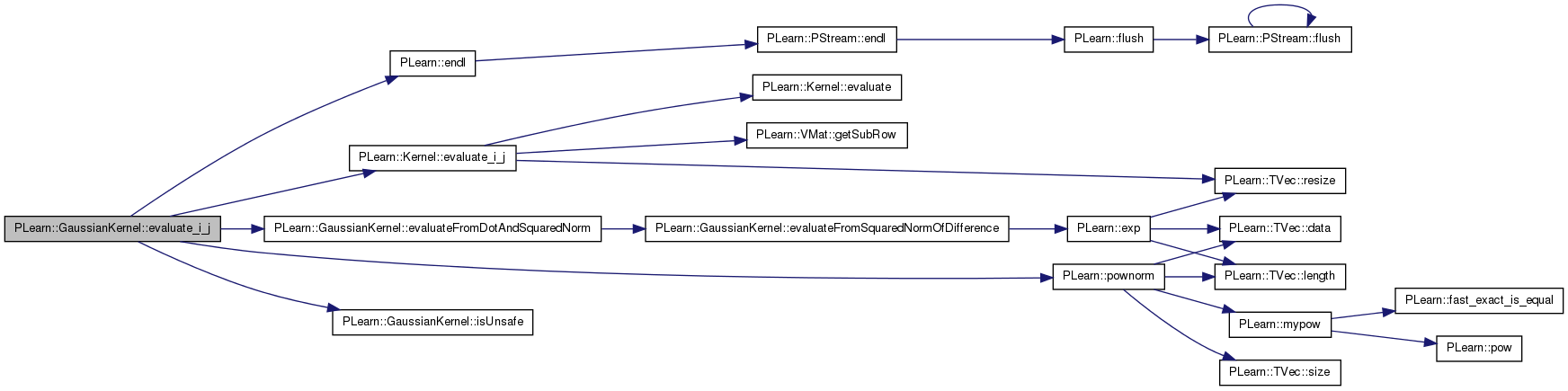
returns evaluate(data(i),data(j))
Reimplemented from PLearn::Kernel.
Definition at line 194 of file GaussianKernel.cc.
References PLearn::Kernel::data, PLearn::Kernel::data_inputsize, PLearn::endl(), PLearn::Kernel::evaluate_i_j(), evaluateFromDotAndSquaredNorm(), i, isUnsafe(), j, PLERROR, PLearn::pownorm(), and squarednorms.
{
#ifdef GK_DEBUG
if(i==0 && j==1){
cout << "*** i==0 && j==1 ***" << endl;
cout << "data(" << i << "): " << data(i) << endl << endl;
cout << "data(" << j << "): " << data(j) << endl << endl;
real sqnorm_i = pownorm((Vec)data(i), 2);
if(sqnorm_i != squarednorms[i])
PLERROR("%f = sqnorm_i != squarednorms[%d] = %f", sqnorm_i, i, squarednorms[i]);
real sqnorm_j = pownorm((Vec)data(j), 2);
if(sqnorm_j != squarednorms[j])
PLERROR("%f = sqnorm_j != squarednorms[%d] = %f", sqnorm_j, j, squarednorms[j]);
}
#endif
real sqn_i = squarednorms[i];
real sqn_j = squarednorms[j];
if (isUnsafe(sqn_i, sqn_j))
return inherited::evaluate_i_j(i,j);
else
return evaluateFromDotAndSquaredNorm(sqn_i, data->dot(i,j,data_inputsize), sqn_j);
}
| real PLearn::GaussianKernel::evaluate_i_x | ( | int | i, |
| const Vec & | x, | ||
| real | squared_norm_of_x = -1 |
||
| ) | const [virtual] |
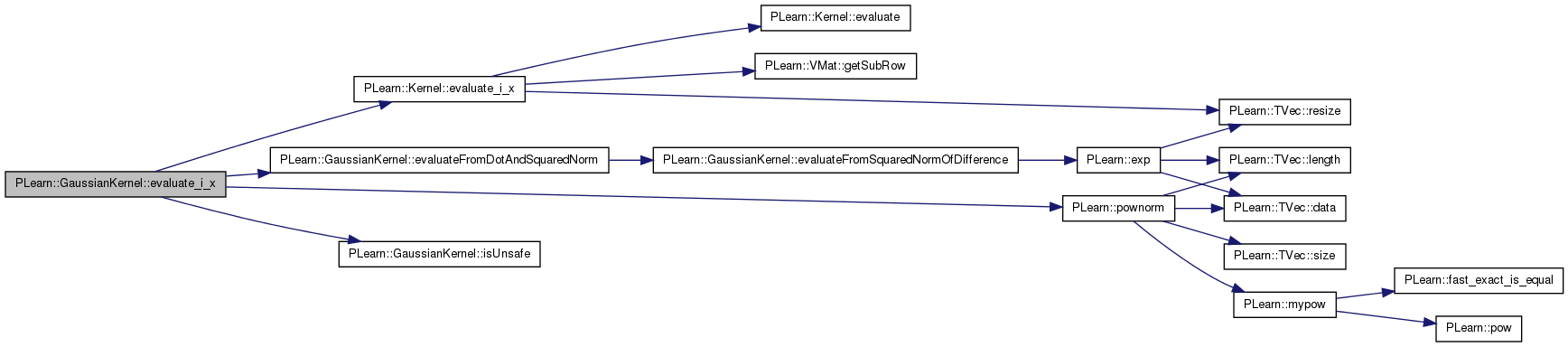
returns evaluate(data(i),x)
Reimplemented from PLearn::Kernel.
Definition at line 222 of file GaussianKernel.cc.
References PLearn::Kernel::data, PLearn::Kernel::evaluate_i_x(), evaluateFromDotAndSquaredNorm(), i, isUnsafe(), PLearn::pownorm(), and squarednorms.
{
if(squared_norm_of_x<0.)
squared_norm_of_x = pownorm(x);
#ifdef GK_DEBUG
// real dot_x1_x2 = data->dot(i,x);
// cout << "data.row(" << i << "): " << data.row(i) << endl
// << "squarednorms[" << i << "]: " << squarednorms[i] << endl
// << "data->dot(i,x): " << dot_x1_x2 << endl
// << "x: " << x << endl
// << "squared_norm_of_x: " << squared_norm_of_x << endl;
// real sqnorm_of_diff = (squarednorms[i]+squared_norm_of_x)-(dot_x1_x2+dot_x1_x2);
// cout << "a-> sqnorm_of_diff: " << sqnorm_of_diff << endl
// << "b-> minus_one_over_sigmasquare: " << minus_one_over_sigmasquare << endl
// << "a*b: " << sqnorm_of_diff*minus_one_over_sigmasquare << endl
// << "res: " << exp(sqnorm_of_diff*minus_one_over_sigmasquare) << endl;
#endif
real sqn_i = squarednorms[i];
if (isUnsafe(sqn_i, squared_norm_of_x))
return inherited::evaluate_i_x(i, x, squared_norm_of_x);
else
return evaluateFromDotAndSquaredNorm(sqn_i, data->dot(i,x), squared_norm_of_x);
}
| real PLearn::GaussianKernel::evaluate_x_i | ( | const Vec & | x, |
| int | i, | ||
| real | squared_norm_of_x = -1 |
||
| ) | const [virtual] |
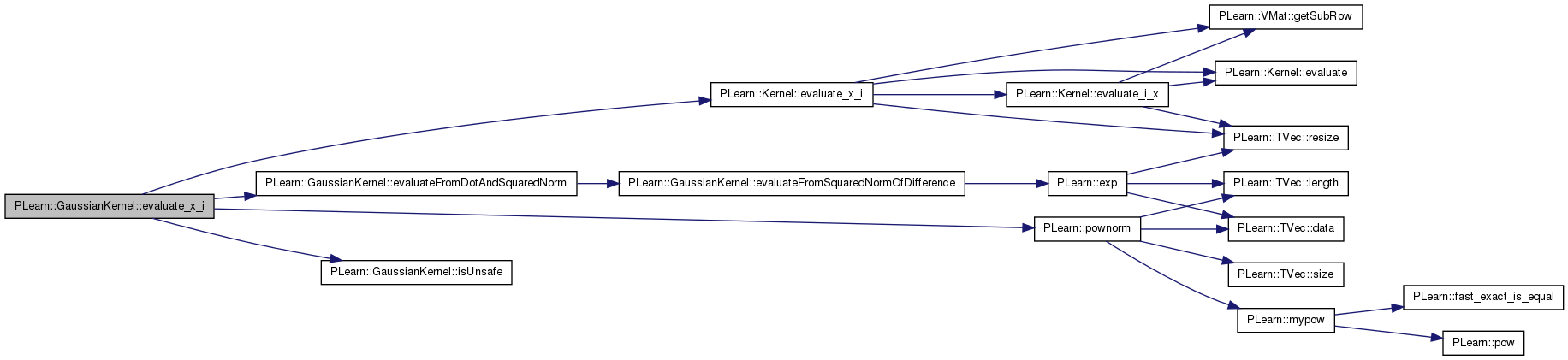
returns evaluate(x,data(i))
Reimplemented from PLearn::Kernel.
Definition at line 251 of file GaussianKernel.cc.
References PLearn::Kernel::data, PLearn::Kernel::evaluate_x_i(), evaluateFromDotAndSquaredNorm(), i, isUnsafe(), PLearn::pownorm(), and squarednorms.
{
if(squared_norm_of_x<0.)
squared_norm_of_x = pownorm(x);
real sqn_i = squarednorms[i];
if (isUnsafe(sqn_i, squared_norm_of_x))
return inherited::evaluate_x_i(x, i, squared_norm_of_x);
else
return evaluateFromDotAndSquaredNorm(squared_norm_of_x, data->dot(i,x), sqn_i);
}
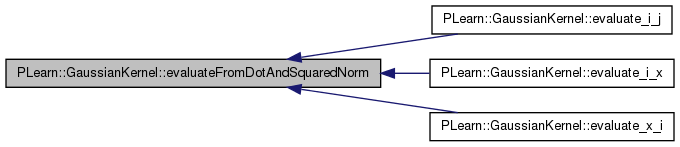
| real PLearn::GaussianKernel::evaluateFromDotAndSquaredNorm | ( | real | sqnorm_x1, |
| real | dot_x1_x2, | ||
| real | sqnorm_x2 | ||
| ) | const [inline, private] |
Definition at line 162 of file GaussianKernel.cc.
References evaluateFromSquaredNormOfDifference().
Referenced by evaluate_i_j(), evaluate_i_x(), and evaluate_x_i().
{
return evaluateFromSquaredNormOfDifference((sqnorm_x1+sqnorm_x2)-(dot_x1_x2+dot_x1_x2));
}

| real PLearn::GaussianKernel::evaluateFromSquaredNormOfDifference | ( | real | sqnorm_of_diff | ) | const [inline, private] |
Definition at line 139 of file GaussianKernel.cc.
References PLearn::exp(), minus_one_over_sigmasquare, PLERROR, scale_by_sigma, and sigmasquare_over_two.
Referenced by evaluate(), and evaluateFromDotAndSquaredNorm().
{
if (sqnorm_of_diff < 0) {
if (sqnorm_of_diff * minus_one_over_sigmasquare < 1e-10 )
// This can still happen when computing K(x,x), because of numerical
// approximations.
sqnorm_of_diff = 0;
else {
// This should not happen (anymore) with the isUnsafe check.
// You may comment out the PLERROR below if you want to continue your
// computations, but then you should investigate why this happens.
PLERROR("In GaussianKernel::evaluateFromSquaredNormOfDifference - The given "
"'sqnorm_of_diff' is negative (%f)", sqnorm_of_diff);
sqnorm_of_diff = 0;
}
}
if (scale_by_sigma) {
return exp(sqnorm_of_diff*minus_one_over_sigmasquare) * sigmasquare_over_two;
} else {
return exp(sqnorm_of_diff*minus_one_over_sigmasquare);
}
}


| OptionList & PLearn::GaussianKernel::getOptionList | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 57 of file GaussianKernel.cc.
| OptionMap & PLearn::GaussianKernel::getOptionMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 57 of file GaussianKernel.cc.
| RemoteMethodMap & PLearn::GaussianKernel::getRemoteMethodMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 57 of file GaussianKernel.cc.
Return true if estimating the squared difference of two points x1 and x2 from their squared norms sqn_1 and sqn_2 (and their dot product) might lead to unsafe numerical approximations.
Specifically, it will return true when ||x1||^2 > 1e6 and | ||x2||^2 / ||x1||^2 - 1 | < 0.01 i.e. when the two points have a large similar norm.
Definition at line 265 of file GaussianKernel.cc.
Referenced by evaluate_i_j(), evaluate_i_x(), and evaluate_x_i().
{
return (sqn_1 > 1e6 && fabs(sqn_2 / sqn_1 - 1.0) < 1e-2);
}
| void PLearn::GaussianKernel::makeDeepCopyFromShallowCopy | ( | CopiesMap & | copies | ) | [virtual] |
Does the necessary operations to transform a shallow copy (this) into a deep copy by deep-copying all the members that need to be.
This needs to be overridden by every class that adds "complex" data members to the class, such as Vec, Mat, PP<Something>, etc. Typical implementation:
void CLASS_OF_THIS::makeDeepCopyFromShallowCopy(CopiesMap& copies) { inherited::makeDeepCopyFromShallowCopy(copies); deepCopyField(complex_data_member1, copies); deepCopyField(complex_data_member2, copies); ... }
| copies | A map used by the deep-copy mechanism to keep track of already-copied objects. |
Reimplemented from PLearn::Kernel.
Definition at line 109 of file GaussianKernel.cc.
References PLearn::deepCopyField(), PLearn::Kernel::makeDeepCopyFromShallowCopy(), and squarednorms.
{
inherited::makeDeepCopyFromShallowCopy(copies);
deepCopyField(squarednorms,copies);
}

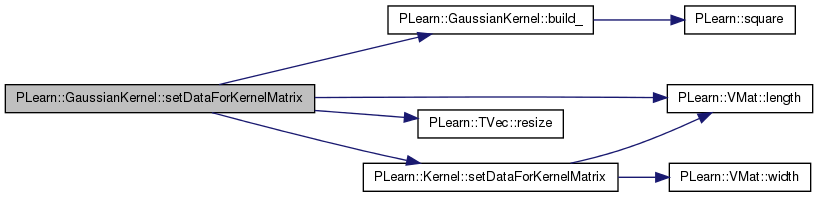
| void PLearn::GaussianKernel::setDataForKernelMatrix | ( | VMat | the_data | ) | [virtual] |
This method precomputes the squared norm for all the data to later speed up evaluate methods.
Reimplemented from PLearn::Kernel.
Definition at line 272 of file GaussianKernel.cc.
References build_(), PLearn::Kernel::data, PLearn::Kernel::data_inputsize, PLearn::VMat::length(), PLearn::TVec< T >::resize(), PLearn::Kernel::setDataForKernelMatrix(), and squarednorms.
{
inherited::setDataForKernelMatrix(the_data);
build_(); // Update sigma computation cache
squarednorms.resize(data.length());
for(int index=0; index<data.length(); index++)
squarednorms[index] = data->dot(index,index, data_inputsize);
}
| void PLearn::GaussianKernel::setParameters | ( | Vec | paramvec | ) | [virtual] |
** Subclasses may override these methods ** They provide a generic way to set and retrieve kernel parameters
default version produces an error
Reimplemented from PLearn::Kernel.
Definition at line 284 of file GaussianKernel.cc.
References build_(), PLWARNING, and sigma.
{
PLWARNING("In GaussianKernel: setParameters is deprecated, use setOption instead");
sigma = paramvec[0];
build_(); // Update sigma computation cache
}

Reimplemented from PLearn::Kernel.
Definition at line 82 of file GaussianKernel.h.
-1 / sigma^2
Definition at line 69 of file GaussianKernel.h.
Referenced by build_(), and evaluateFromSquaredNormOfDifference().
Build options below.
Definition at line 64 of file GaussianKernel.h.
Referenced by declareOptions(), and evaluateFromSquaredNormOfDifference().
Definition at line 65 of file GaussianKernel.h.
Referenced by build_(), declareOptions(), and setParameters().
real PLearn::GaussianKernel::sigmasquare_over_two [protected] |
sigma^2 / 2
Definition at line 70 of file GaussianKernel.h.
Referenced by build_(), and evaluateFromSquaredNormOfDifference().
Vec PLearn::GaussianKernel::squarednorms [protected] |
squarednorms of the rows of the data VMat (data is a member of Kernel)
Definition at line 72 of file GaussianKernel.h.
Referenced by addDataForKernelMatrix(), evaluate_i_j(), evaluate_i_x(), evaluate_x_i(), makeDeepCopyFromShallowCopy(), and setDataForKernelMatrix().
 1.7.4
1.7.4