|
PLearn 0.1
|
|
PLearn 0.1
|
#include <Kernel.h>
Inherits PLearn::Object.
Inherited by PLearn::BetaKernel, PLearn::BinaryKernelDiscrimination, PLearn::ClassDistanceProportionCostFunction, PLearn::ClassErrorCostFunction, PLearn::ClassMarginCostFunction, PLearn::CompactVMatrixGaussianKernel, PLearn::CompactVMatrixPolynomialKernel, PLearn::ConvexBasisKernel, PLearn::CorrelationKernel, PLearn::DifferenceKernel, PLearn::DirectNegativeCostFunction, PLearn::DistanceKernel, PLearn::DotProductKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::GaussianDensityKernel, PLearn::GaussianKernel, PLearn::GeneralizedDistanceRBFKernel, PLearn::GeodesicDistanceKernel, PLearn::LaplacianKernel, PLearn::LiftBinaryCostFunction, PLearn::LLEKernel, PLearn::LogOfGaussianDensityKernel, PLearn::ManifoldParzenKernel, PLearn::MemoryCachedKernel, PLearn::MulticlassErrorCostFunction, PLearn::NegKernel, PLearn::NegLogProbCostFunction, PLearn::NegOutputCostFunction, PLearn::NonLocalManifoldParzenKernel, PLearn::NormalizedDotProductKernel, PLearn::PartsDistanceKernel, PLearn::PolynomialKernel, PLearn::PowDistanceKernel, PLearn::PrecomputedKernel, PLearn::PricingTransactionPairProfitFunction, PLearn::QuadraticUtilityCostFunction, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::ScaledLaplacianKernel, PLearn::SelectedOutputCostFunction, PLearn::SigmoidalKernel, PLearn::SigmoidPrimitiveKernel, PLearn::SourceKernel, PLearn::SquaredErrorCostFunction, PLearn::SummationKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedDistance, and PLearn::WeightedQuadraticPolynomialKernel.
Public Member Functions | |
| Kernel (bool is__symmetric=true, bool call_build_=false) | |
| Constructor. | |
| virtual Kernel * | deepCopy (CopiesMap &copies) const |
| virtual real | evaluate (const Vec &x1, const Vec &x2) const =0 |
| ** Subclasses must override this method ** | |
| virtual void | train (VMat data) |
| Subclasses may override this method for kernels that can be trained on a dataset prior to being used (e.g. | |
| virtual void | setDataForKernelMatrix (VMat the_data) |
| ** Subclasses may override these methods to provide efficient kernel matrix access ** | |
| virtual void | addDataForKernelMatrix (const Vec &newRow) |
| This method is meant to be used any time the data matrix is appended a new row by an outer instance (e.g. | |
| int | dataInputsize () const |
| Return data_inputsize. | |
| int | nExamples () const |
| Return n_examples. | |
| virtual real | evaluate_i_j (int i, int j) const |
| returns evaluate(data(i),data(j)) | |
| virtual real | evaluate_i_x (int i, const Vec &x, real squared_norm_of_x=-1) const |
| Return evaluate(data(i),x). | |
| virtual real | evaluate_x_i (const Vec &x, int i, real squared_norm_of_x=-1) const |
| returns evaluate(x,data(i)) [default version calls evaluate_i_x if kernel is_symmetric] | |
| virtual real | evaluate_i_x_again (int i, const Vec &x, real squared_norm_of_x=-1, bool first_time=false) const |
| Return evaluate(data(i),x), where x is the same as in the precedent call to this same function (except if 'first_time' is true). | |
| virtual real | evaluate_x_i_again (const Vec &x, int i, real squared_norm_of_x=-1, bool first_time=false) const |
| virtual void | computeGramMatrix (Mat K) const |
| Call evaluate_i_j to fill each of the entries (i,j) of symmetric matrix K. | |
| virtual Mat | returnComputedGramMatrix () const |
| virtual void | computePartialGramMatrix (const TVec< int > &subset_indices, Mat K) const |
| Compute a partial Gram matrix between all pairs of a subset of elements (length M) of the Kernel data matrix. | |
| virtual void | computeTestGramMatrix (Mat test_elements, Mat K, Vec self_cov) const |
| Compute a cross-covariance matrix between the given test elements (length M) and the elements of the Kernel data matrix (length N). | |
| virtual void | computeSparseGramMatrix (TVec< Mat > K) const |
| Fill K[i] with the non-zero elements of row i of the Gram matrix. | |
| virtual void | computeGramMatrixDerivative (Mat &KD, const string &kernel_param, real epsilon=1e-6) const |
| Compute the derivative of the Gram matrix with respect to one of the kernel's parameters. | |
| virtual void | setParameters (Vec paramvec) |
| ** Subclasses may override these methods ** They provide a generic way to set and retrieve kernel parameters | |
| virtual Vec | getParameters () const |
| default version returns an empty Vec | |
| virtual void | evaluate_all_i_x (const Vec &x, const Vec &k_xi_x, real squared_norm_of_x=-1, int istart=0) const |
| Fill k_xi_x with K(x_i, x), for all i from istart to istart + k_xi_x.length() - 1. | |
| virtual void | evaluate_all_x_i (const Vec &x, const Vec &k_x_xi, real squared_norm_of_x=-1, int istart=0) const |
| Fill k_x_xi with K(x, x_i), for all i from istart to istart + k_x_xi.length() - 1. | |
| void | apply (VMat m1, VMat m2, Mat &result) const |
| ** Subclasses should NOT override the following methods. The default versions are fine. ** | |
| Mat | apply (VMat m1, VMat m2) const |
| same as above, but returns the result mat instead | |
| void | apply (VMat m, const Vec &x, Vec &result) const |
| result[i]=K(m[i],x) | |
| void | apply (Vec x, VMat m, Vec &result) const |
| result[i]=K(x,m[i]) | |
| real | operator() (const Vec &x1, const Vec &x2) const |
| bool | hasData () |
| Return true iif there is a data matrix set for this kernel. | |
| VMat | getData () |
| Return the data matrix set for this kernel. | |
| bool | isInData (const Vec &x, int *i=0) const |
| Return true iff the point x is in the kernel dataset. | |
| void | computeNearestNeighbors (const Vec &x, Mat &k_xi_x_sorted, int knn) const |
| Fill 'k_xi_x_sorted' with the value of K(x, x_i) for all training points x_i in the first column (with the knn first ones being sorted according to increasing value of K(x, x_i)), and with the indices of the corresponding neighbors in the second column. | |
| Mat | estimateHistograms (VMat d, real sameness_threshold, real minval, real maxval, int nbins) const |
| Mat | estimateHistograms (Mat input_and_class, real minval, real maxval, int nbins) const |
| real | test (VMat d, real threshold, real sameness_below_threshold, real sameness_above_threshold) const |
| virtual void | build () |
| Post-constructor. | |
| virtual | ~Kernel () |
| virtual void | makeDeepCopyFromShallowCopy (CopiesMap &copies) |
| Does the necessary operations to transform a shallow copy (this) into a deep copy by deep-copying all the members that need to be. | |
Static Public Member Functions | |
| static string | _classname_ () |
| static OptionList & | _getOptionList_ () |
| static RemoteMethodMap & | _getRemoteMethodMap_ () |
| static bool | _isa_ (const Object *o) |
| static void | _static_initialize_ () |
| static const PPath & | declaringFile () |
| static TMat< int > | computeKNNeighbourMatrixFromDistanceMatrix (const Mat &D, int knn, bool insure_self_first_neighbour=true, bool report_progress=false) |
| Returns a Mat m such that m(i,j) is the index of jth closest neighbour of input i, according to the "distance" measures given by D(i,j). | |
| static Mat | computeNeighbourMatrixFromDistanceMatrix (const Mat &D, bool insure_self_first_neighbour=true, bool report_progress=false) |
| Returns a Mat m such that m(i,j) is the index of jth closest neighbour of input i, according to the "distance" measures given by D(i,j) You should use computeKNNeighbourMatrixFromDistanceMatrix instead. | |
Public Attributes | |
| bool | cache_gram_matrix |
| Build options. | |
| bool | is_symmetric |
| int | report_progress |
| VMat | specify_dataset |
Static Public Attributes | |
| static StaticInitializer | _static_initializer_ |
Static Protected Member Functions | |
| static void | declareOptions (OptionList &ol) |
| Declare options (data fields) for the class. | |
| static void | declareMethods (RemoteMethodMap &rmm) |
| Declare the methods that are remote-callable. | |
Protected Attributes | |
| VMat | data |
| data for kernel matrix, which will be used for calls to evaluate_i_j and the like | |
| int | data_inputsize |
| Mat | gram_matrix |
| Cached Gram matrix. | |
| TVec< Mat > | sparse_gram_matrix |
| Cached sparse Gram matrix. | |
| bool | gram_matrix_is_cached |
| bool | sparse_gram_matrix_is_cached |
| int | n_examples |
Private Types | |
| typedef Object | inherited |
Private Member Functions | |
| void | build_ () |
| Object-specific post-constructor. | |
Private Attributes | |
| Vec | evaluate_xi |
| Used to store data to save memory allocation. | |
| Vec | evaluate_xj |
| Vec | k_xi_x |
| bool | lock_xi |
| Used to make sure we do not accidentally overwrite some global data. | |
| bool | lock_xj |
| bool | lock_k_xi_x |
typedef Object PLearn::Kernel::inherited [private] |
Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::ClassDistanceProportionCostFunction, PLearn::ClassErrorCostFunction, PLearn::ClassMarginCostFunction, PLearn::CompactVMatrixGaussianKernel, PLearn::CompactVMatrixPolynomialKernel, PLearn::ConvexBasisKernel, PLearn::CorrelationKernel, PLearn::CosKernel, PLearn::DifferenceKernel, PLearn::DirectNegativeCostFunction, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::PartsDistanceKernel, PLearn::GaussianDensityKernel, PLearn::GaussianKernel, PLearn::GeneralizedDistanceRBFKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LaplacianKernel, PLearn::LiftBinaryCostFunction, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::LogOfGaussianDensityKernel, PLearn::ManifoldParzenKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::MulticlassErrorCostFunction, PLearn::NegKernel, PLearn::NegLogProbCostFunction, PLearn::NegOutputCostFunction, PLearn::NeuralNetworkARDKernel, PLearn::NonLocalManifoldParzenKernel, PLearn::NormalizedDotProductKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PowDistanceKernel, PLearn::PrecomputedKernel, PLearn::PricingTransactionPairProfitFunction, PLearn::QuadraticUtilityCostFunction, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::ScaledLaplacianKernel, PLearn::SelectedOutputCostFunction, PLearn::SigmoidalKernel, PLearn::SigmoidPrimitiveKernel, PLearn::SourceKernel, PLearn::SquaredErrorCostFunction, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedQuadraticPolynomialKernel, PLearn::WeightedDistance, and PLearn::BinaryKernelDiscrimination.
Constructor.
Definition at line 66 of file Kernel.cc.
References build_().
:
inherited(call_build_),
lock_xi(false),
lock_xj(false),
lock_k_xi_x(false),
data_inputsize(-1),
gram_matrix_is_cached(false),
sparse_gram_matrix_is_cached(false),
n_examples(-1),
cache_gram_matrix(false),
is_symmetric(is__symmetric),
report_progress(0)
{
if (call_build_)
build_();
}

| string PLearn::Kernel::_classname_ | ( | ) | [static] |
Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::ClassDistanceProportionCostFunction, PLearn::ClassErrorCostFunction, PLearn::ClassMarginCostFunction, PLearn::CompactVMatrixGaussianKernel, PLearn::CompactVMatrixPolynomialKernel, PLearn::ConvexBasisKernel, PLearn::CorrelationKernel, PLearn::CosKernel, PLearn::DifferenceKernel, PLearn::DirectNegativeCostFunction, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::PartsDistanceKernel, PLearn::GaussianDensityKernel, PLearn::GaussianKernel, PLearn::GeneralizedDistanceRBFKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LaplacianKernel, PLearn::LiftBinaryCostFunction, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::LogOfGaussianDensityKernel, PLearn::ManifoldParzenKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::MulticlassErrorCostFunction, PLearn::NegKernel, PLearn::NegLogProbCostFunction, PLearn::NegOutputCostFunction, PLearn::NeuralNetworkARDKernel, PLearn::NonLocalManifoldParzenKernel, PLearn::NormalizedDotProductKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PowDistanceKernel, PLearn::PrecomputedKernel, PLearn::PricingTransactionPairProfitFunction, PLearn::QuadraticUtilityCostFunction, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::ScaledLaplacianKernel, PLearn::SelectedOutputCostFunction, PLearn::SigmoidalKernel, PLearn::SigmoidPrimitiveKernel, PLearn::SourceKernel, PLearn::SquaredErrorCostFunction, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedQuadraticPolynomialKernel, PLearn::WeightedDistance, and PLearn::BinaryKernelDiscrimination.
| OptionList & PLearn::Kernel::_getOptionList_ | ( | ) | [static] |
Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::ClassDistanceProportionCostFunction, PLearn::ClassErrorCostFunction, PLearn::ClassMarginCostFunction, PLearn::CompactVMatrixGaussianKernel, PLearn::CompactVMatrixPolynomialKernel, PLearn::ConvexBasisKernel, PLearn::CorrelationKernel, PLearn::CosKernel, PLearn::DifferenceKernel, PLearn::DirectNegativeCostFunction, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::PartsDistanceKernel, PLearn::GaussianDensityKernel, PLearn::GaussianKernel, PLearn::GeneralizedDistanceRBFKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LaplacianKernel, PLearn::LiftBinaryCostFunction, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::LogOfGaussianDensityKernel, PLearn::ManifoldParzenKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::MulticlassErrorCostFunction, PLearn::NegKernel, PLearn::NegLogProbCostFunction, PLearn::NegOutputCostFunction, PLearn::NeuralNetworkARDKernel, PLearn::NonLocalManifoldParzenKernel, PLearn::NormalizedDotProductKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PowDistanceKernel, PLearn::PrecomputedKernel, PLearn::PricingTransactionPairProfitFunction, PLearn::QuadraticUtilityCostFunction, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::ScaledLaplacianKernel, PLearn::SelectedOutputCostFunction, PLearn::SigmoidalKernel, PLearn::SigmoidPrimitiveKernel, PLearn::SourceKernel, PLearn::SquaredErrorCostFunction, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedQuadraticPolynomialKernel, PLearn::WeightedDistance, and PLearn::BinaryKernelDiscrimination.
| RemoteMethodMap & PLearn::Kernel::_getRemoteMethodMap_ | ( | ) | [static] |
Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::ClassDistanceProportionCostFunction, PLearn::ClassErrorCostFunction, PLearn::ClassMarginCostFunction, PLearn::CompactVMatrixGaussianKernel, PLearn::CompactVMatrixPolynomialKernel, PLearn::ConvexBasisKernel, PLearn::CorrelationKernel, PLearn::CosKernel, PLearn::DifferenceKernel, PLearn::DirectNegativeCostFunction, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::PartsDistanceKernel, PLearn::GaussianDensityKernel, PLearn::GaussianKernel, PLearn::GeneralizedDistanceRBFKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LaplacianKernel, PLearn::LiftBinaryCostFunction, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::LogOfGaussianDensityKernel, PLearn::ManifoldParzenKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::MulticlassErrorCostFunction, PLearn::NegKernel, PLearn::NegLogProbCostFunction, PLearn::NegOutputCostFunction, PLearn::NeuralNetworkARDKernel, PLearn::NonLocalManifoldParzenKernel, PLearn::NormalizedDotProductKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PowDistanceKernel, PLearn::PrecomputedKernel, PLearn::PricingTransactionPairProfitFunction, PLearn::QuadraticUtilityCostFunction, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::ScaledLaplacianKernel, PLearn::SelectedOutputCostFunction, PLearn::SigmoidalKernel, PLearn::SigmoidPrimitiveKernel, PLearn::SourceKernel, PLearn::SquaredErrorCostFunction, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedQuadraticPolynomialKernel, PLearn::WeightedDistance, and PLearn::BinaryKernelDiscrimination.
Definition at line 60 of file Kernel.cc.
Referenced by PLearn::DTWKernel::declareMethods().

Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::ClassDistanceProportionCostFunction, PLearn::ClassErrorCostFunction, PLearn::ClassMarginCostFunction, PLearn::CompactVMatrixGaussianKernel, PLearn::CompactVMatrixPolynomialKernel, PLearn::ConvexBasisKernel, PLearn::CorrelationKernel, PLearn::CosKernel, PLearn::DifferenceKernel, PLearn::DirectNegativeCostFunction, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::PartsDistanceKernel, PLearn::GaussianDensityKernel, PLearn::GaussianKernel, PLearn::GeneralizedDistanceRBFKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LaplacianKernel, PLearn::LiftBinaryCostFunction, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::LogOfGaussianDensityKernel, PLearn::ManifoldParzenKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::MulticlassErrorCostFunction, PLearn::NegKernel, PLearn::NegLogProbCostFunction, PLearn::NegOutputCostFunction, PLearn::NeuralNetworkARDKernel, PLearn::NonLocalManifoldParzenKernel, PLearn::NormalizedDotProductKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PowDistanceKernel, PLearn::PrecomputedKernel, PLearn::PricingTransactionPairProfitFunction, PLearn::QuadraticUtilityCostFunction, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::ScaledLaplacianKernel, PLearn::SelectedOutputCostFunction, PLearn::SigmoidalKernel, PLearn::SigmoidPrimitiveKernel, PLearn::SourceKernel, PLearn::SquaredErrorCostFunction, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedQuadraticPolynomialKernel, PLearn::WeightedDistance, and PLearn::BinaryKernelDiscrimination.
| StaticInitializer Kernel::_static_initializer_ & PLearn::Kernel::_static_initialize_ | ( | ) | [static] |
Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::ClassDistanceProportionCostFunction, PLearn::ClassErrorCostFunction, PLearn::ClassMarginCostFunction, PLearn::CompactVMatrixGaussianKernel, PLearn::CompactVMatrixPolynomialKernel, PLearn::ConvexBasisKernel, PLearn::CorrelationKernel, PLearn::CosKernel, PLearn::DifferenceKernel, PLearn::DirectNegativeCostFunction, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::PartsDistanceKernel, PLearn::GaussianDensityKernel, PLearn::GaussianKernel, PLearn::GeneralizedDistanceRBFKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LaplacianKernel, PLearn::LiftBinaryCostFunction, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::LogOfGaussianDensityKernel, PLearn::ManifoldParzenKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::MulticlassErrorCostFunction, PLearn::NegKernel, PLearn::NegLogProbCostFunction, PLearn::NegOutputCostFunction, PLearn::NeuralNetworkARDKernel, PLearn::NonLocalManifoldParzenKernel, PLearn::NormalizedDotProductKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PowDistanceKernel, PLearn::PrecomputedKernel, PLearn::PricingTransactionPairProfitFunction, PLearn::QuadraticUtilityCostFunction, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::ScaledLaplacianKernel, PLearn::SelectedOutputCostFunction, PLearn::SigmoidalKernel, PLearn::SigmoidPrimitiveKernel, PLearn::SourceKernel, PLearn::SquaredErrorCostFunction, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedQuadraticPolynomialKernel, PLearn::WeightedDistance, and PLearn::BinaryKernelDiscrimination.
| void PLearn::Kernel::addDataForKernelMatrix | ( | const Vec & | newRow | ) | [virtual] |
This method is meant to be used any time the data matrix is appended a new row by an outer instance (e.g.
SequentialKernel). Through this method, the kernel must update any data dependent internal structure. The internal structures should have consistent length with the data matrix, assuming a sequential growing of the vmat.
Reimplemented in PLearn::GaussianKernel, PLearn::ManifoldParzenKernel, PLearn::MemoryCachedKernel, PLearn::PrecomputedKernel, PLearn::SourceKernel, PLearn::SummationKernel, and PLearn::VMatKernel.
Definition at line 206 of file Kernel.cc.
Referenced by PLearn::GaussianKernel::addDataForKernelMatrix(), and PLearn::MemoryCachedKernel::addDataForKernelMatrix().
{
try{
data->appendRow(newRow);
}
catch(const PLearnError&){
PLERROR("Kernel::addDataForKernelMatrix: if one intends to use this method,\n"
"he must provide a data matrix for which the appendRow method is\n"
"implemented.");
}
}

result[i]=K(m[i],x)
Definition at line 716 of file Kernel.cc.
References evaluate(), PLearn::VMat::getSubRow(), i, PLearn::VMat::length(), PLearn::TVec< T >::resize(), and PLearn::VMat::width().
{
result.resize(m->length());
int mw = m->inputsize();
if (mw == -1) { // No inputsize specified: using width instead.
mw = m->width();
}
Vec m_i(mw);
for(int i=0; i<m->length(); i++)
{
m->getSubRow(i,0,m_i);
result[i] = evaluate(m_i,x);
}
}
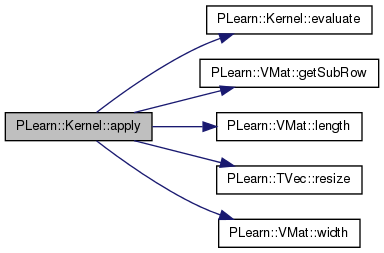
result[i]=K(x,m[i])
Definition at line 732 of file Kernel.cc.
References evaluate(), PLearn::VMat::getSubRow(), i, PLearn::VMat::length(), PLearn::TVec< T >::resize(), and PLearn::VMat::width().
{
result.resize(m->length());
int mw = m->inputsize();
if (mw == -1) { // No inputsize specified: using width instead.
mw = m->width();
}
Vec m_i(mw);
for(int i=0; i<m->length(); i++)
{
m->getSubRow(i,0,m_i);
result[i] = evaluate(x,m_i);
}
}
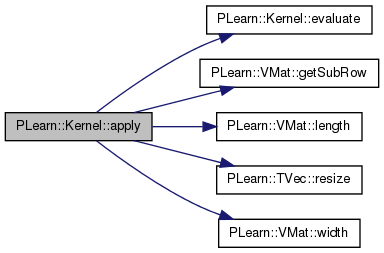
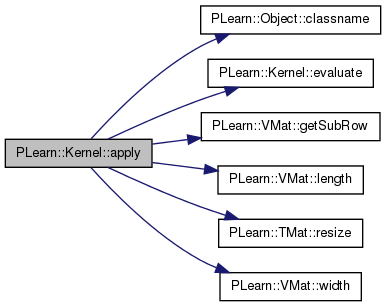
** Subclasses should NOT override the following methods. The default versions are fine. **
result(i,j) = K(m1(i),m2(j))
Definition at line 652 of file Kernel.cc.
References PLearn::Object::classname(), evaluate(), PLearn::VMat::getSubRow(), i, is_symmetric, j, PLearn::VMat::length(), report_progress, PLearn::TMat< T >::resize(), and PLearn::VMat::width().
Referenced by apply().
{
result.resize(m1->length(), m2->length());
int m1w = m1->inputsize();
if (m1w == -1) { // No inputsize specified: using width instead.
m1w = m1->width();
}
int m2w = m2->inputsize();
if (m2w == -1) {
m2w = m2->width();
}
Vec m1_i(m1w);
Vec m2_j(m2w);
PP<ProgressBar> pb;
bool easy_case = (is_symmetric && m1 == m2);
int l1 = m1->length();
int l2 = m2->length();
if (report_progress) {
int nb_steps;
if (easy_case) {
nb_steps = (l1 * (l1 + 1)) / 2;
} else {
nb_steps = l1 * l2;
}
pb = new ProgressBar("Applying " + classname() + " to two matrices", nb_steps);
}
int count = 0;
if(easy_case)
{
for(int i=0; i<m1->length(); i++)
{
m1->getSubRow(i,0,m1_i);
for(int j=0; j<=i; j++)
{
m2->getSubRow(j,0,m2_j);
real val = evaluate(m1_i,m2_j);
result(i,j) = val;
result(j,i) = val;
}
if (pb) {
count += i + 1;
pb->update(count);
}
}
}
else
{
for(int i=0; i<m1->length(); i++)
{
m1->getSubRow(i,0,m1_i);
for(int j=0; j<m2->length(); j++)
{
m2->getSubRow(j,0,m2_j);
result(i,j) = evaluate(m1_i,m2_j);
}
if (pb) {
count += l2;
pb->update(count);
}
}
}
}

| void PLearn::Kernel::build | ( | ) | [virtual] |
Post-constructor.
The normal implementation should call simply inherited::build(), then this class's build_(). This method should be callable again at later times, after modifying some option fields to change the "architecture" of the object.
Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::CorrelationKernel, PLearn::DivisiveNormalizationKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::GaussianKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::NeuralNetworkARDKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PrecomputedKernel, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::SourceKernel, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedQuadraticPolynomialKernel, and PLearn::BinaryKernelDiscrimination.
Definition at line 147 of file Kernel.cc.
References PLearn::Object::build(), and build_().
Referenced by PLearn::WeightedQuadraticPolynomialKernel::build(), PLearn::ReconstructionWeightsKernel::build(), PLearn::PolynomialKernel::build(), PLearn::MemoryCachedKernel::build(), PLearn::LLEKernel::build(), PLearn::GeodesicDistanceKernel::build(), PLearn::GaussianKernel::build(), PLearn::EpanechnikovKernel::build(), PLearn::DTWKernel::build(), PLearn::CorrelationKernel::build(), PLearn::BinaryKernelDiscrimination::build(), PLearn::BetaKernel::build(), PLearn::RemoveDuplicateVMatrix::build_(), PLearn::KNNVMatrix::build_(), and computeGramMatrixDerivative().
{
inherited::build();
build_();
}

| void PLearn::Kernel::build_ | ( | ) | [private] |
Object-specific post-constructor.
This method should be redefined in subclasses and do the actual building of the object according to previously set option fields. Constructors can just set option fields, and then call build_. This method is NOT virtual, and will typically be called only from three places: a constructor, the public virtual build() method, and possibly the public virtual read method (which calls its parent's read). build_() can assume that its parent's build_() has already been called.
Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::CorrelationKernel, PLearn::DivisiveNormalizationKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::GaussianKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::NeuralNetworkARDKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PrecomputedKernel, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::SourceKernel, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedQuadraticPolynomialKernel, and PLearn::BinaryKernelDiscrimination.
Definition at line 155 of file Kernel.cc.
References setDataForKernelMatrix(), and specify_dataset.
Referenced by build(), and Kernel().
{
if (specify_dataset) {
this->setDataForKernelMatrix(specify_dataset);
}
}

| void PLearn::Kernel::computeGramMatrix | ( | Mat | K | ) | const [virtual] |
Call evaluate_i_j to fill each of the entries (i,j) of symmetric matrix K.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::DivisiveNormalizationKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::Matern1ARDKernel, PLearn::NeuralNetworkARDKernel, PLearn::PLearnerDiagonalKernel, PLearn::RationalQuadraticARDKernel, PLearn::SourceKernel, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, and PLearn::VMatKernel.
Definition at line 361 of file Kernel.cc.
References cache_gram_matrix, PLearn::Object::classname(), data, evaluate_i_j(), gram_matrix, gram_matrix_is_cached, i, is_symmetric, PLearn::PP< T >::isNotNull(), j, PLearn::VMat::length(), PLearn::TMat< T >::length(), m, PLearn::TMat< T >::mod(), PLASSERT, PLERROR, report_progress, PLearn::TMat< T >::resize(), and PLearn::TMat< T >::width().
Referenced by PLearn::RemoveDuplicateVMatrix::build_(), PLearn::KNNVMatrix::build_(), computeGramMatrixDerivative(), PLearn::GaussianProcessNLLVariable::fbpropFragments(), and returnComputedGramMatrix().
{
if (!data)
PLERROR("Kernel::computeGramMatrix should be called only after setDataForKernelMatrix");
if (!is_symmetric)
PLERROR("In Kernel::computeGramMatrix - Currently not implemented for non-symmetric kernels");
if (cache_gram_matrix && gram_matrix_is_cached) {
K << gram_matrix;
return;
}
if (K.length() != data.length() || K.width() != data.length())
PLERROR("Kernel::computeGramMatrix: the argument matrix K should be\n"
"of size %d x %d (currently of size %d x %d)",
data.length(), data.length(), K.length(), K.width());
int l=data->length();
int m=K.mod();
PP<ProgressBar> pb;
int count = 0;
if (report_progress)
pb = new ProgressBar("Computing Gram matrix for " + classname(), (l * (l + 1)) / 2);
real Kij;
real* Ki;
real* Kji_;
for (int i=0;i<l;i++)
{
Ki = K[i];
Kji_ = &K[0][i];
for (int j=0; j<=i; j++,Kji_+=m)
{
Kij = evaluate_i_j(i,j);
*Ki++ = Kij;
if (j<i)
*Kji_ = Kij;
}
if (report_progress) {
count += i + 1;
PLASSERT( pb.isNotNull() );
pb->update(count);
}
}
if (cache_gram_matrix) {
gram_matrix.resize(l,l);
gram_matrix << K;
gram_matrix_is_cached = true;
}
}

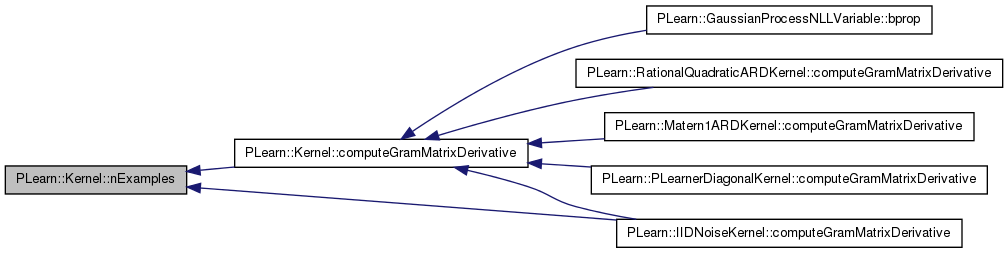
| void PLearn::Kernel::computeGramMatrixDerivative | ( | Mat & | KD, |
| const string & | kernel_param, | ||
| real | epsilon = 1e-6 |
||
| ) | const [virtual] |
Compute the derivative of the Gram matrix with respect to one of the kernel's parameters.
The default implementation is to perform this operation by finite difference (using the specified epsilon), but specific kernels may override this in the interest of speed and memory consumption (which requires, in the default implementation, a second Gram matrix in intermediate storage). The kernel parameter is specified using the getOption/setOption syntax.
< Temporarily necessary
< Temporarily necessary
< Temporarily necessary
Reimplemented in PLearn::IIDNoiseKernel, PLearn::LinearARDKernel, PLearn::Matern1ARDKernel, PLearn::NeuralNetworkARDKernel, PLearn::PLearnerDiagonalKernel, PLearn::RationalQuadraticARDKernel, PLearn::SquaredExponentialARDKernel, and PLearn::SummationKernel.
Definition at line 585 of file Kernel.cc.
References build(), cache_gram_matrix, PLearn::Object::changeOption(), computeGramMatrix(), data, PLearn::endl(), PLearn::Object::getOption(), PLearn::lexical_cast(), nExamples(), PLERROR, PLearn::TMat< T >::resize(), and PLearn::tostring().
Referenced by PLearn::GaussianProcessNLLVariable::bprop(), PLearn::RationalQuadraticARDKernel::computeGramMatrixDerivative(), PLearn::Matern1ARDKernel::computeGramMatrixDerivative(), PLearn::PLearnerDiagonalKernel::computeGramMatrixDerivative(), and PLearn::IIDNoiseKernel::computeGramMatrixDerivative().
{
MODULE_LOG << "Computing Gram matrix derivative by finite differences "
<< "for hyper-parameter '" << kernel_param << "'"
<< endl;
// This function is conceptually const, but the evaluation by finite
// differences in a generic way requires some change-options, which
// formally require a const-away cast.
Kernel* This = const_cast<Kernel*>(this);
bool old_cache = cache_gram_matrix;
This->cache_gram_matrix = false;
if (!data)
PLERROR("Kernel::computeGramMatrixDerivative should be called only after "
"setDataForKernelMatrix");
int W = nExamples();
KD.resize(W,W);
Mat KDminus(W,W);
string cur_param_str = getOption(kernel_param);
real cur_param = lexical_cast<real>(cur_param_str);
// Compute the positive part of the finite difference
This->changeOption(kernel_param, tostring(cur_param+epsilon));
This->build();
computeGramMatrix(KD);
// Compute the negative part of the finite difference
This->changeOption(kernel_param, tostring(cur_param-epsilon));
This->build();
computeGramMatrix(KDminus);
// Finalize computation
KD -= KDminus;
KD /= real(2.*epsilon);
This->changeOption(kernel_param, cur_param_str);
This->build();
This->cache_gram_matrix = old_cache;
}
| TMat< int > PLearn::Kernel::computeKNNeighbourMatrixFromDistanceMatrix | ( | const Mat & | D, |
| int | knn, | ||
| bool | insure_self_first_neighbour = true, |
||
| bool | report_progress = false |
||
| ) | [static] |
Returns a Mat m such that m(i,j) is the index of jth closest neighbour of input i, according to the "distance" measures given by D(i,j).
Only knn neighbours are computed.
Definition at line 788 of file Kernel.cc.
References PLearn::TMat< T >::column(), i, j, PLearn::TMat< T >::length(), PLearn::partialSortRows(), and PLearn::TMat< T >::subMatRows().
Referenced by PLearn::ReconstructionWeightsKernel::computeWeights(), and PLearn::GeodesicDistanceKernel::setDataForKernelMatrix().
{
int npoints = D.length();
TMat<int> neighbours(npoints, knn);
Mat tmpsort(npoints,2);
PP<ProgressBar> pb;
if (report_progress) {
pb = new ProgressBar("Computing neighbour matrix", npoints);
}
Mat indices;
for(int i=0; i<npoints; i++)
{
for(int j=0; j<npoints; j++)
{
tmpsort(j,0) = D(i,j);
tmpsort(j,1) = j;
}
if(insure_self_first_neighbour)
tmpsort(i,0) = -FLT_MAX;
partialSortRows(tmpsort, knn);
indices = tmpsort.column(1).subMatRows(0,knn);
for (int j = 0; j < knn; j++) {
neighbours(i,j) = int(indices(j,0));
}
if (pb)
pb->update(i);
}
return neighbours;
}

Fill 'k_xi_x_sorted' with the value of K(x, x_i) for all training points x_i in the first column (with the knn first ones being sorted according to increasing value of K(x, x_i)), and with the indices of the corresponding neighbors in the second column.
Definition at line 333 of file Kernel.cc.
References evaluate_all_i_x(), i, k_xi_x, lock_k_xi_x, n_examples, PLearn::partialSortRows(), PLearn::TMat< T >::resize(), and PLearn::TVec< T >::resize().
{
Vec k_val;
bool unlock = true;
if (lock_k_xi_x) {
k_val.resize(n_examples);
unlock = false;
}
else {
lock_k_xi_x = true;
k_xi_x.resize(n_examples);
k_val = k_xi_x;
}
k_xi_x_sorted.resize(n_examples, 2);
// Compute the distance from x to all training points.
evaluate_all_i_x(x, k_val);
// Find the knn nearest neighbors.
for (int i = 0; i < n_examples; i++) {
k_xi_x_sorted(i,0) = k_val[i];
k_xi_x_sorted(i,1) = real(i);
}
partialSortRows(k_xi_x_sorted, knn);
if (unlock)
lock_k_xi_x = false;
}
| Mat PLearn::Kernel::computeNeighbourMatrixFromDistanceMatrix | ( | const Mat & | D, |
| bool | insure_self_first_neighbour = true, |
||
| bool | report_progress = false |
||
| ) | [static] |
Returns a Mat m such that m(i,j) is the index of jth closest neighbour of input i, according to the "distance" measures given by D(i,j) You should use computeKNNeighbourMatrixFromDistanceMatrix instead.
Definition at line 825 of file Kernel.cc.
References PLearn::TMat< T >::column(), i, j, PLearn::TMat< T >::length(), and PLearn::sortRows().
Referenced by PLearn::KNNVMatrix::build_().
{
int npoints = D.length();
Mat neighbours(npoints, npoints);
Mat tmpsort(npoints,2);
PP<ProgressBar> pb;
if (report_progress) {
pb = new ProgressBar("Computing neighbour matrix", npoints);
}
//for(int i=0; i<2; i++)
for(int i=0; i<npoints; i++)
{
for(int j=0; j<npoints; j++)
{
tmpsort(j,0) = D(i,j);
tmpsort(j,1) = j;
}
if(insure_self_first_neighbour)
tmpsort(i,0) = -FLT_MAX;
sortRows(tmpsort);
neighbours(i) << tmpsort.column(1);
if (pb)
pb->update(i);
}
return neighbours;
}


| void PLearn::Kernel::computePartialGramMatrix | ( | const TVec< int > & | subset_indices, |
| Mat | K | ||
| ) | const [virtual] |
Compute a partial Gram matrix between all pairs of a subset of elements (length M) of the Kernel data matrix.
This is stored in matrix K (assumed to be preallocated to M x M). The subset_indices should be SORTED in order of increasing indices.
Definition at line 422 of file Kernel.cc.
References PLearn::Object::classname(), data, evaluate_i_j(), i, is_symmetric, PLearn::PP< T >::isNotNull(), j, PLearn::TMat< T >::length(), PLearn::TVec< T >::length(), m, PLearn::TMat< T >::mod(), PLASSERT, PLERROR, report_progress, PLearn::TVec< T >::size(), and PLearn::TMat< T >::width().
{
if (!data)
PLERROR("Kernel::computePartialGramMatrix should be called only after setDataForKernelMatrix");
if (!is_symmetric)
PLERROR("In Kernel::computePartialGramMatrix - Currently not implemented for non-symmetric kernels");
if (K.length() != subset_indices.length() || K.width() != subset_indices.length())
PLERROR("Kernel::computePartialGramMatrix: the argument matrix K should be\n"
"of size %d x %d (currently of size %d x %d)",
subset_indices.length(), subset_indices.length(), K.length(), K.width());
int l=subset_indices.size();
int m=K.mod();
PP<ProgressBar> pb;
int count = 0;
if (report_progress)
pb = new ProgressBar("Computing Partial Gram matrix for " + classname(),
(l * (l + 1)) / 2);
real Kij;
real* Ki;
real* Kji_;
for (int i=0;i<l;i++)
{
int index_i = subset_indices[i];
Ki = K[i];
Kji_ = &K[0][i];
for (int j=0; j<=i; j++,Kji_+=m)
{
int index_j = subset_indices[j];
Kij = evaluate_i_j(index_i, index_j);
*Ki++ = Kij;
if (j<i)
*Kji_ = Kij;
}
if (report_progress) {
count += i + 1;
PLASSERT( pb.isNotNull() );
pb->update(count);
}
}
}
Fill K[i] with the non-zero elements of row i of the Gram matrix.
Specifically, K[i] is a (k_i x 2) matrix where k_i is the number of non-zero elements in the i-th row of the Gram matrix, and K[i](k) = [<index of k-th non-zero element> <value of k-th non-zero element>]
Definition at line 507 of file Kernel.cc.
References PLearn::TMat< T >::appendRow(), cache_gram_matrix, PLearn::Object::classname(), data, evaluate_i_j(), PLearn::fast_exact_is_equal(), gram_matrix, gram_matrix_is_cached, i, is_symmetric, j, PLearn::TVec< T >::length(), PLearn::VMat::length(), n, PLERROR, report_progress, PLearn::TMat< T >::resize(), PLearn::TVec< T >::resize(), sparse_gram_matrix, and sparse_gram_matrix_is_cached.
{
if (!data) PLERROR("Kernel::computeSparseGramMatrix should be called only after setDataForKernelMatrix");
if (!is_symmetric)
PLERROR("In Kernel::computeGramMatrix - Currently not implemented for non-symmetric kernels");
if (cache_gram_matrix && sparse_gram_matrix_is_cached) {
for (int i = 0; i < sparse_gram_matrix.length(); i++) {
K[i].resize(sparse_gram_matrix[i].length(), 2);
K[i] << sparse_gram_matrix[i];
}
return;
}
if (cache_gram_matrix && gram_matrix_is_cached) {
// We can obtain the sparse Gram matrix from the full one.
int n = K.length();
Vec row(2);
for (int i = 0; i < n; i++) {
Mat& K_i = K[i];
K_i.resize(0,2);
real* gram_ij = gram_matrix[i];
for (int j = 0; j < n; j++, gram_ij++)
if (!fast_exact_is_equal(*gram_ij, 0)) {
row[0] = j;
row[1] = *gram_ij;
K_i.appendRow(row);
}
}
// TODO Use a method to avoid code duplication below.
sparse_gram_matrix.resize(n);
for (int i = 0; i < n; i++) {
sparse_gram_matrix[i].resize(K[i].length(), 2);
sparse_gram_matrix[i] << K[i];
}
sparse_gram_matrix_is_cached = true;
return;
}
int l=data->length();
PP<ProgressBar> pb;
int count = 0;
if (report_progress) {
pb = new ProgressBar("Computing sparse Gram matrix for " + classname(), (l * (l + 1)) / 2);
}
Vec j_and_Kij(2);
for (int i = 0; i < l; i++)
K[i].resize(0,2);
for (int i=0;i<l;i++)
{
for (int j=0; j<=i; j++)
{
j_and_Kij[1] = evaluate_i_j(i,j);
if (!fast_exact_is_equal(j_and_Kij[1], 0)) {
j_and_Kij[0] = j;
K[i].appendRow(j_and_Kij);
if (j < i) {
j_and_Kij[0] = i;
K[j].appendRow(j_and_Kij);
}
}
}
if (pb) {
count += i + 1;
pb->update(count);
}
}
if (cache_gram_matrix) {
sparse_gram_matrix.resize(l);
for (int i = 0; i < l; i++) {
sparse_gram_matrix[i].resize(K[i].length(), 2);
sparse_gram_matrix[i] << K[i];
}
sparse_gram_matrix_is_cached = true;
}
}
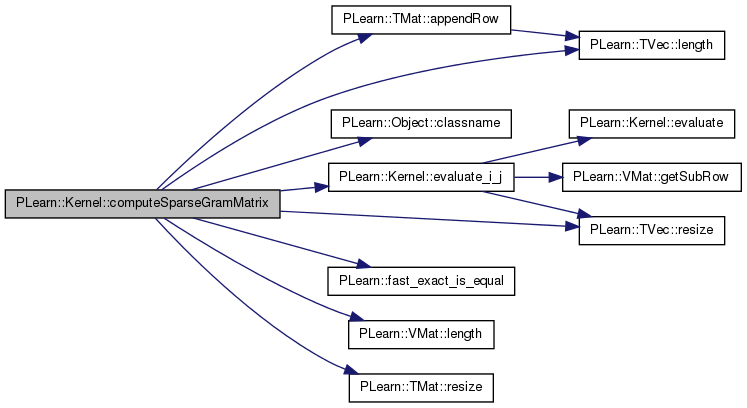
| void PLearn::Kernel::computeTestGramMatrix | ( | Mat | test_elements, |
| Mat | K, | ||
| Vec | self_cov | ||
| ) | const [virtual] |
Compute a cross-covariance matrix between the given test elements (length M) and the elements of the Kernel data matrix (length N).
This is stored in matrix K (assumed to be preallocated to M x N). The self-covariance of the test elements is further stored in the vector test_cov (assumed to be preallocated to size M). (This is useful for some kernels used in Gaussian Processes, since there is a difference between vector equality and vector identity regarding how sampling noise is treated.)
Definition at line 467 of file Kernel.cc.
References PLearn::Object::classname(), data, evaluate(), evaluate_all_i_x(), i, PLearn::TMat< T >::length(), PLearn::VMat::length(), n, PLERROR, report_progress, PLearn::TVec< T >::size(), PLearn::VMat::width(), and PLearn::TMat< T >::width().
{
if (!data)
PLERROR("Kernel::computeTestGramMatrix should be called only after setDataForKernelMatrix");
if (test_elements.width() != data.width())
PLERROR("Kernel::computeTestGramMatrix: the input matrix test_elements "
"should be of width %d (currently of width %d)",
data.width(), test_elements.width());
if (K.length() != test_elements.length() || K.width() != data.length())
PLERROR("Kernel::computeTestGramMatrix: the output matrix K should be\n"
"of size %d x %d (currently of size %d x %d)",
test_elements.length(), data.length(), K.length(), K.width());
if (self_cov.size() != test_elements.length())
PLERROR("Kernel::computeTestGramMatrix: the output vector self_cov should be\n"
"of length %d (currently of length %d)",
test_elements.length(), self_cov.size());
int n=test_elements.length();
PP<ProgressBar> pb = report_progress?
new ProgressBar("Computing Test Gram matrix for " + classname(), n)
: 0;
for (int i=0 ; i<n ; ++i)
{
Vec cur_test_elem = test_elements(i);
evaluate_all_i_x(cur_test_elem, K(i));
self_cov[i] = evaluate(cur_test_elem, cur_test_elem);
if (pb)
pb->update(i);
}
}
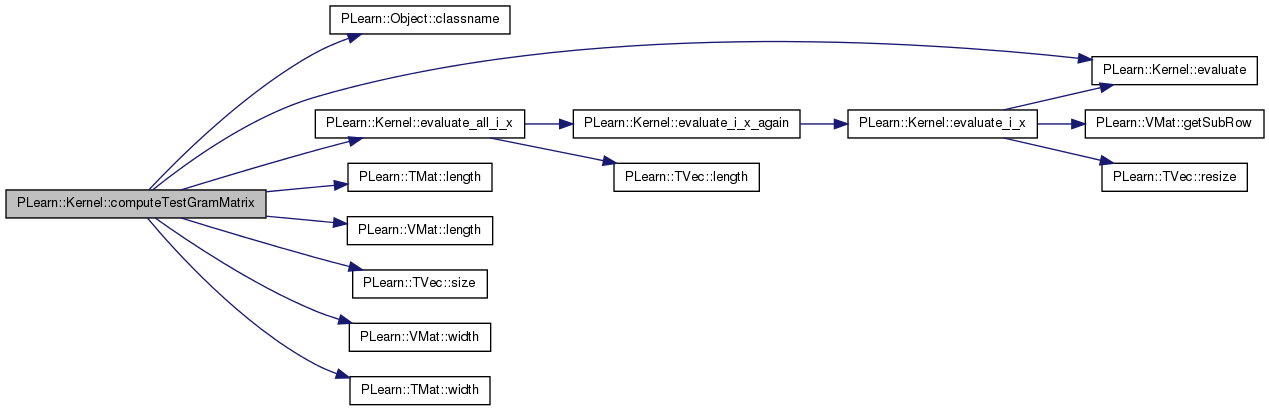
| int PLearn::Kernel::dataInputsize | ( | ) | const [inline] |
Return data_inputsize.
Definition at line 123 of file Kernel.h.
Referenced by PLearn::Matern1ARDKernel::computeGramMatrix(), PLearn::RationalQuadraticARDKernel::computeGramMatrix(), PLearn::MemoryCachedKernel::dataRow(), and PLearn::RationalQuadraticARDKernel::evaluate_all_i_x().
{
return data_inputsize;
}
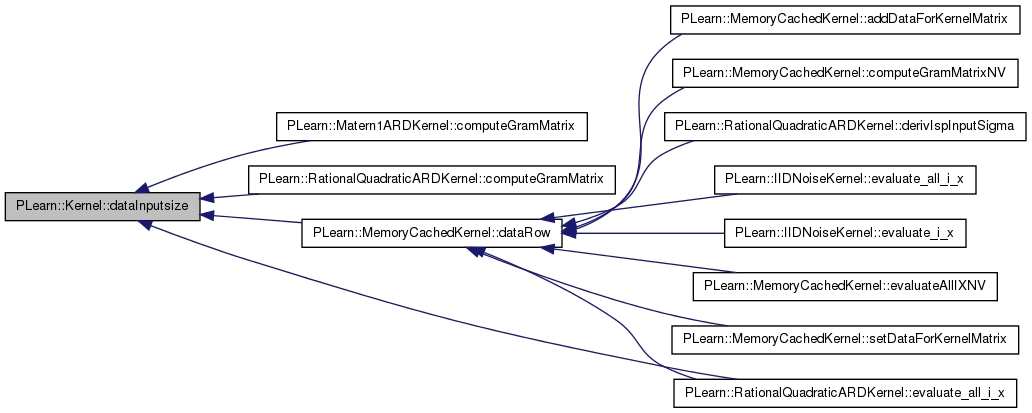
| void PLearn::Kernel::declareMethods | ( | RemoteMethodMap & | rmm | ) | [static, protected] |
Declare the methods that are remote-callable.
Reimplemented from PLearn::Object.
Reimplemented in PLearn::DTWKernel.
Definition at line 118 of file Kernel.cc.
References PLearn::Object::_getRemoteMethodMap_(), PLearn::declareMethod(), evaluate(), PLearn::RemoteMethodMap::inherited(), returnComputedGramMatrix(), and setDataForKernelMatrix().
{
// Insert a backpointer to remote methods; note that this
// different than for declareOptions()
rmm.inherited(inherited::_getRemoteMethodMap_());
declareMethod(
rmm, "returnComputedGramMatrix", &Kernel::returnComputedGramMatrix,
(BodyDoc("\n"),
RetDoc ("Returns the Gram Matrix")));
declareMethod(
rmm, "evaluate", &Kernel::evaluate,
(BodyDoc("Evaluate the kernel on two vectors\n"),
ArgDoc("x1","first vector"),
ArgDoc("x2","second vector"),
RetDoc ("K(x1,x2)")));
declareMethod(
rmm, "setDataForKernelMatrix", &Kernel::setDataForKernelMatrix,
(BodyDoc("This method sets the data VMat that will be used to define the kernel\n"
"matrix. It may precompute values from this that may later accelerate\n"
"the evaluation of a kernel matrix element\n"),
ArgDoc("data", "The data matrix to set into the kernel")));
}
| void PLearn::Kernel::declareOptions | ( | OptionList & | ol | ) | [static, protected] |
Declare options (data fields) for the class.
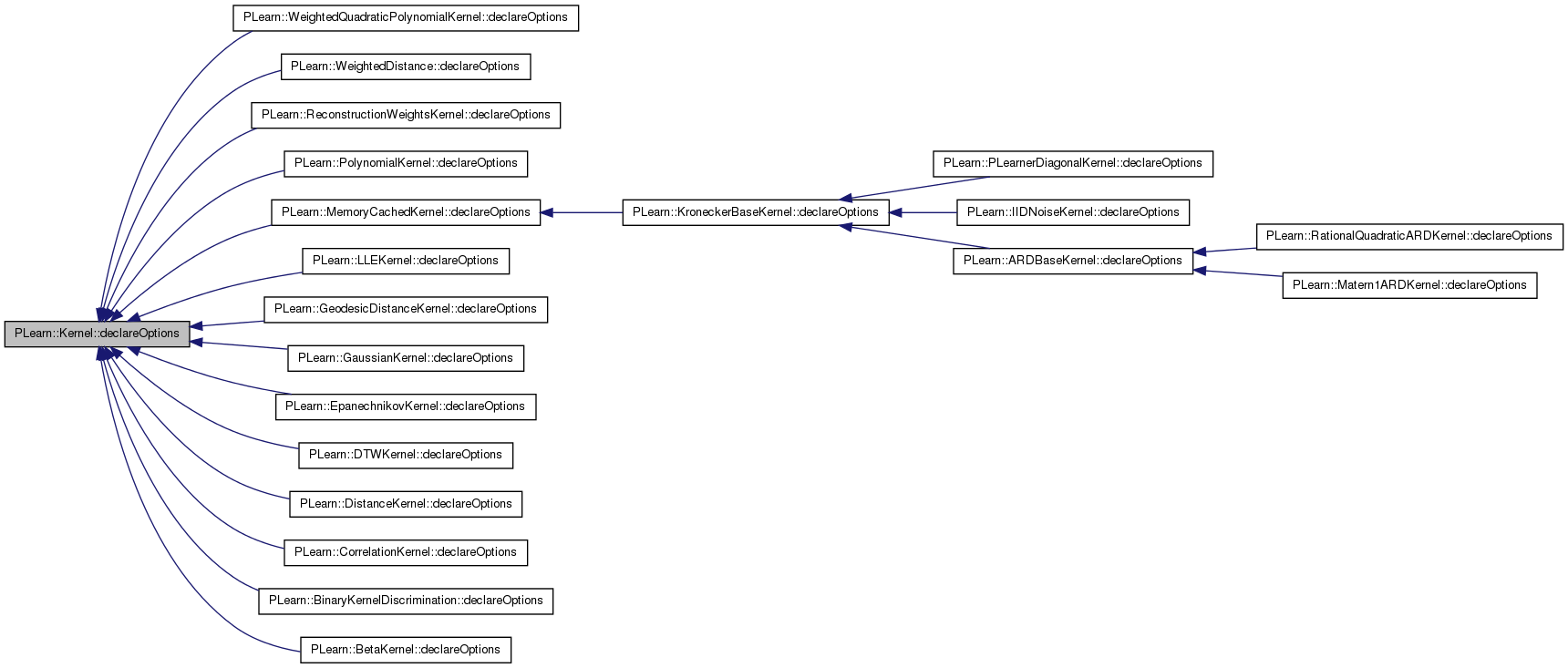
Redefine this in subclasses: call declareOption(...) for each option, and then call inherited::declareOptions(options). Please call the inherited method AT THE END to get the options listed in a consistent order (from most recently defined to least recently defined).
static void MyDerivedClass::declareOptions(OptionList& ol) { declareOption(ol, "inputsize", &MyObject::inputsize_, OptionBase::buildoption, "The size of the input; it must be provided"); declareOption(ol, "weights", &MyObject::weights, OptionBase::learntoption, "The learned model weights"); inherited::declareOptions(ol); }
| ol | List of options that is progressively being constructed for the current class. |
Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::ClassErrorCostFunction, PLearn::ClassMarginCostFunction, PLearn::CompactVMatrixGaussianKernel, PLearn::CompactVMatrixPolynomialKernel, PLearn::ConvexBasisKernel, PLearn::CorrelationKernel, PLearn::CosKernel, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::PartsDistanceKernel, PLearn::GaussianDensityKernel, PLearn::GaussianKernel, PLearn::GeneralizedDistanceRBFKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LaplacianKernel, PLearn::LiftBinaryCostFunction, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::LogOfGaussianDensityKernel, PLearn::ManifoldParzenKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::NegKernel, PLearn::NegLogProbCostFunction, PLearn::NeuralNetworkARDKernel, PLearn::NonLocalManifoldParzenKernel, PLearn::NormalizedDotProductKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PowDistanceKernel, PLearn::PrecomputedKernel, PLearn::PricingTransactionPairProfitFunction, PLearn::QuadraticUtilityCostFunction, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::SelectedOutputCostFunction, PLearn::SigmoidalKernel, PLearn::SigmoidPrimitiveKernel, PLearn::SourceKernel, PLearn::SquaredErrorCostFunction, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedQuadraticPolynomialKernel, PLearn::WeightedDistance, and PLearn::BinaryKernelDiscrimination.
Definition at line 86 of file Kernel.cc.
References PLearn::OptionBase::buildoption, cache_gram_matrix, data_inputsize, PLearn::declareOption(), PLearn::Object::declareOptions(), is_symmetric, PLearn::OptionBase::learntoption, n_examples, report_progress, and specify_dataset.
Referenced by PLearn::WeightedQuadraticPolynomialKernel::declareOptions(), PLearn::WeightedDistance::declareOptions(), PLearn::ReconstructionWeightsKernel::declareOptions(), PLearn::PolynomialKernel::declareOptions(), PLearn::MemoryCachedKernel::declareOptions(), PLearn::LLEKernel::declareOptions(), PLearn::GeodesicDistanceKernel::declareOptions(), PLearn::GaussianKernel::declareOptions(), PLearn::EpanechnikovKernel::declareOptions(), PLearn::DTWKernel::declareOptions(), PLearn::DistanceKernel::declareOptions(), PLearn::CorrelationKernel::declareOptions(), PLearn::BinaryKernelDiscrimination::declareOptions(), and PLearn::BetaKernel::declareOptions().
{
// Build options.
declareOption(ol, "is_symmetric", &Kernel::is_symmetric, OptionBase::buildoption,
"Whether this kernel is symmetric or not.");
declareOption(ol, "report_progress", &Kernel::report_progress, OptionBase::buildoption,
"If set to 1, a progress bar will be displayed when computing the Gram matrix,\n"
"or for other possibly costly operations.");
declareOption(ol, "specify_dataset", &Kernel::specify_dataset, OptionBase::buildoption,
"If set, then setDataForKernelMatrix will be called with this dataset at build time");
declareOption(ol, "cache_gram_matrix", &Kernel::cache_gram_matrix, OptionBase::buildoption,
"If set to 1, the Gram matrix will be cached in memory to avoid multiple computations.");
// Learnt options.
declareOption(ol, "data_inputsize", &Kernel::data_inputsize, OptionBase::learntoption,
"The inputsize of 'data' (if -1, is set to data.width()).");
declareOption(ol, "n_examples", &Kernel::n_examples, OptionBase::learntoption,
"The number of examples in 'data'.");
inherited::declareOptions(ol);
}

| static const PPath& PLearn::Kernel::declaringFile | ( | ) | [inline, static] |
Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::ClassDistanceProportionCostFunction, PLearn::ClassErrorCostFunction, PLearn::ClassMarginCostFunction, PLearn::CompactVMatrixGaussianKernel, PLearn::CompactVMatrixPolynomialKernel, PLearn::ConvexBasisKernel, PLearn::CorrelationKernel, PLearn::CosKernel, PLearn::DifferenceKernel, PLearn::DirectNegativeCostFunction, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::PartsDistanceKernel, PLearn::GaussianDensityKernel, PLearn::GaussianKernel, PLearn::GeneralizedDistanceRBFKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LaplacianKernel, PLearn::LiftBinaryCostFunction, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::LogOfGaussianDensityKernel, PLearn::ManifoldParzenKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::MulticlassErrorCostFunction, PLearn::NegKernel, PLearn::NegLogProbCostFunction, PLearn::NegOutputCostFunction, PLearn::NeuralNetworkARDKernel, PLearn::NonLocalManifoldParzenKernel, PLearn::NormalizedDotProductKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PowDistanceKernel, PLearn::PrecomputedKernel, PLearn::PricingTransactionPairProfitFunction, PLearn::QuadraticUtilityCostFunction, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::ScaledLaplacianKernel, PLearn::SelectedOutputCostFunction, PLearn::SigmoidalKernel, PLearn::SigmoidPrimitiveKernel, PLearn::SourceKernel, PLearn::SquaredErrorCostFunction, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedQuadraticPolynomialKernel, PLearn::WeightedDistance, and PLearn::BinaryKernelDiscrimination.
Definition at line 92 of file Kernel.h.
{
Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::ClassDistanceProportionCostFunction, PLearn::ClassErrorCostFunction, PLearn::ClassMarginCostFunction, PLearn::CompactVMatrixGaussianKernel, PLearn::CompactVMatrixPolynomialKernel, PLearn::ConvexBasisKernel, PLearn::CorrelationKernel, PLearn::CosKernel, PLearn::DifferenceKernel, PLearn::DirectNegativeCostFunction, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::PartsDistanceKernel, PLearn::GaussianDensityKernel, PLearn::GaussianKernel, PLearn::GeneralizedDistanceRBFKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LaplacianKernel, PLearn::LiftBinaryCostFunction, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::LogOfGaussianDensityKernel, PLearn::ManifoldParzenKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::MulticlassErrorCostFunction, PLearn::NegKernel, PLearn::NegLogProbCostFunction, PLearn::NegOutputCostFunction, PLearn::NeuralNetworkARDKernel, PLearn::NonLocalManifoldParzenKernel, PLearn::NormalizedDotProductKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PowDistanceKernel, PLearn::PrecomputedKernel, PLearn::PricingTransactionPairProfitFunction, PLearn::QuadraticUtilityCostFunction, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::ScaledLaplacianKernel, PLearn::SelectedOutputCostFunction, PLearn::SigmoidalKernel, PLearn::SigmoidPrimitiveKernel, PLearn::SourceKernel, PLearn::SquaredErrorCostFunction, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedQuadraticPolynomialKernel, PLearn::WeightedDistance, and PLearn::BinaryKernelDiscrimination.
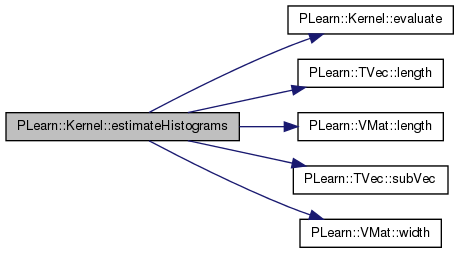
| Mat PLearn::Kernel::estimateHistograms | ( | VMat | d, |
| real | sameness_threshold, | ||
| real | minval, | ||
| real | maxval, | ||
| int | nbins | ||
| ) | const |
Definition at line 858 of file Kernel.cc.
References d, evaluate(), i, PLearn::TVec< T >::length(), PLearn::VMat::length(), PLearn::TVec< T >::subVec(), and PLearn::VMat::width().
{
real binwidth = (maxval-minval)/nbins;
int inputsize = (d->width()-1)/2;
Mat histo(2,nbins);
Vec histo_below = histo(0);
Vec histo_above = histo(1);
int nbelow=0;
int nabove=0;
for(int i=0; i<d->length(); i++)
{
Vec inputs = d(i);
Vec input1 = inputs.subVec(0,inputsize);
Vec input2 = inputs.subVec(inputsize,inputsize);
real sameness = inputs[inputs.length()-1];
real kernelvalue = evaluate(input1,input2);
if(kernelvalue>=minval && kernelvalue<maxval)
{
int binindex = int((kernelvalue-minval)/binwidth);
if(sameness<sameness_threshold)
{
histo_below[binindex]++;
nbelow++;
}
else
{
histo_above[binindex]++;
nabove++;
}
}
}
histo_below /= real(nbelow);
histo_above /= real(nabove);
return histo;
}
| Mat PLearn::Kernel::estimateHistograms | ( | Mat | input_and_class, |
| real | minval, | ||
| real | maxval, | ||
| int | nbins | ||
| ) | const |
Definition at line 895 of file Kernel.cc.
References PLearn::TMat< T >::column(), PLearn::dist(), evaluate(), PLearn::fast_exact_is_equal(), i, j, PLearn::TMat< T >::length(), PLearn::TMat< T >::subMatColumns(), PLearn::sum(), and PLearn::TMat< T >::width().
{
real binwidth = (maxval-minval)/nbins;
int inputsize = input_and_class.width()-1;
Mat inputs = input_and_class.subMatColumns(0,inputsize);
Mat classes = input_and_class.column(inputsize);
Mat histo(4,nbins);
Vec histo_mean_same = histo(0);
Vec histo_mean_other = histo(1);
Vec histo_min_same = histo(2);
Vec histo_min_other = histo(3);
for(int i=0; i<inputs.length(); i++)
{
Vec input = inputs(i);
real input_class = classes(i,0);
real sameclass_meandist = 0.0;
real otherclass_meandist = 0.0;
real sameclass_mindist = FLT_MAX;
real otherclass_mindist = FLT_MAX;
for(int j=0; j<inputs.length(); j++)
if(j!=i)
{
real dist = evaluate(input, inputs(j));
if(fast_exact_is_equal(classes(j,0), input_class))
{
sameclass_meandist += dist;
if(dist<sameclass_mindist)
sameclass_mindist = dist;
}
else
{
otherclass_meandist += dist;
if(dist<otherclass_mindist)
otherclass_mindist = dist;
}
}
sameclass_meandist /= (inputs.length()-1);
otherclass_meandist /= (inputs.length()-1);
if(sameclass_meandist>=minval && sameclass_meandist<maxval)
histo_mean_same[int((sameclass_meandist-minval)/binwidth)]++;
if(sameclass_mindist>=minval && sameclass_mindist<maxval)
histo_min_same[int((sameclass_mindist-minval)/binwidth)]++;
if(otherclass_meandist>=minval && otherclass_meandist<maxval)
histo_mean_other[int((otherclass_meandist-minval)/binwidth)]++;
if(otherclass_mindist>=minval && otherclass_mindist<maxval)
histo_min_other[int((otherclass_mindist-minval)/binwidth)]++;
}
histo_mean_same /= sum(histo_mean_same, false);
histo_min_same /= sum(histo_min_same, false);
histo_mean_other /= sum(histo_mean_other, false);
histo_min_other /= sum(histo_min_other, false);
return histo;
}
** Subclasses must override this method **
returns K(x1,x2)
Implemented in PLearn::AdditiveNormalizationKernel, PLearn::BetaKernel, PLearn::ClassDistanceProportionCostFunction, PLearn::ClassErrorCostFunction, PLearn::ClassMarginCostFunction, PLearn::CompactVMatrixGaussianKernel, PLearn::CompactVMatrixPolynomialKernel, PLearn::ConvexBasisKernel, PLearn::CorrelationKernel, PLearn::CosKernel, PLearn::DifferenceKernel, PLearn::DirectNegativeCostFunction, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::PartsDistanceKernel, PLearn::GaussianDensityKernel, PLearn::GaussianKernel, PLearn::GeneralizedDistanceRBFKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LaplacianKernel, PLearn::LiftBinaryCostFunction, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::LogOfGaussianDensityKernel, PLearn::ManifoldParzenKernel, PLearn::Matern1ARDKernel, PLearn::MulticlassErrorCostFunction, PLearn::NegKernel, PLearn::NegLogProbCostFunction, PLearn::NegOutputCostFunction, PLearn::NeuralNetworkARDKernel, PLearn::NonLocalManifoldParzenKernel, PLearn::NormalizedDotProductKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PowDistanceKernel, PLearn::PrecomputedKernel, PLearn::PricingTransactionPairProfitFunction, PLearn::QuadraticUtilityCostFunction, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::ScaledLaplacianKernel, PLearn::SelectedOutputCostFunction, PLearn::SigmoidalKernel, PLearn::SigmoidPrimitiveKernel, PLearn::SourceKernel, PLearn::SquaredErrorCostFunction, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedQuadraticPolynomialKernel, PLearn::WeightedDistance, and PLearn::BinaryKernelDiscrimination.
Referenced by apply(), computeTestGramMatrix(), declareMethods(), estimateHistograms(), evaluate_i_j(), evaluate_i_x(), evaluate_x_i(), and test().
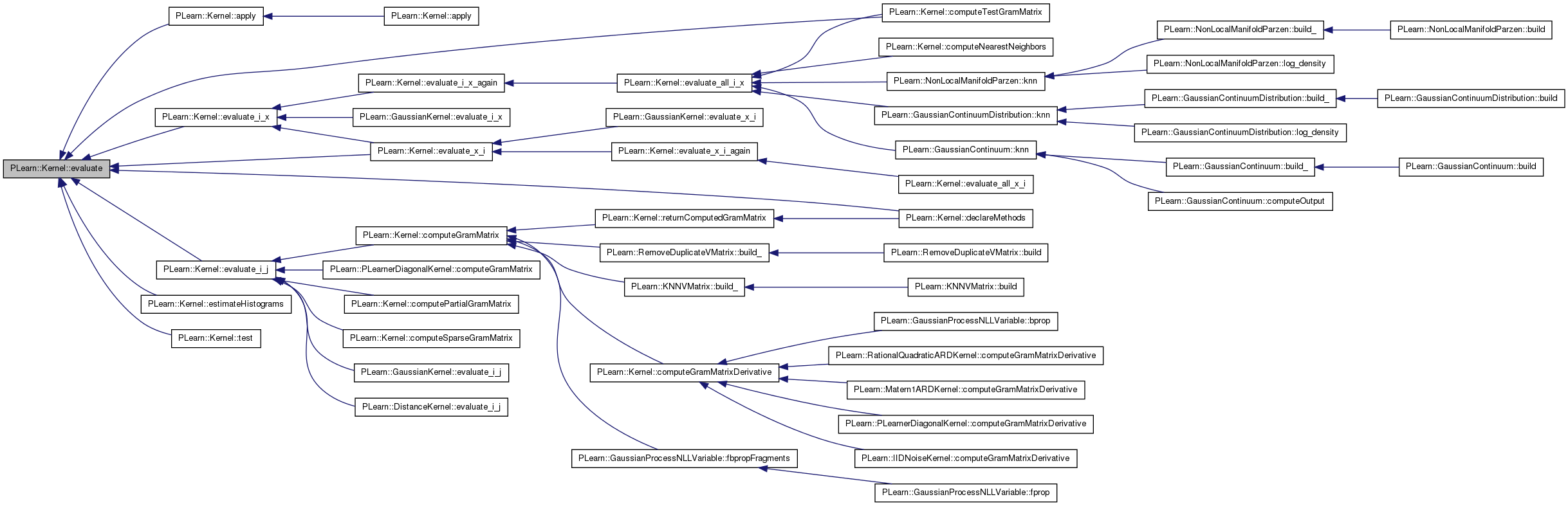
| void PLearn::Kernel::evaluate_all_i_x | ( | const Vec & | x, |
| const Vec & | k_xi_x, | ||
| real | squared_norm_of_x = -1, |
||
| int | istart = 0 |
||
| ) | const [virtual] |
Fill k_xi_x with K(x_i, x), for all i from istart to istart + k_xi_x.length() - 1.
Reimplemented in PLearn::IIDNoiseKernel, PLearn::LinearARDKernel, PLearn::Matern1ARDKernel, PLearn::NeuralNetworkARDKernel, PLearn::PLearnerDiagonalKernel, PLearn::RationalQuadraticARDKernel, PLearn::SquaredExponentialARDKernel, and PLearn::SummationKernel.
Definition at line 304 of file Kernel.cc.
References evaluate_i_x_again(), i, and PLearn::TVec< T >::length().
Referenced by computeNearestNeighbors(), computeTestGramMatrix(), PLearn::NonLocalManifoldParzen::knn(), PLearn::GaussianContinuumDistribution::knn(), and PLearn::GaussianContinuum::knn().
{
k_xi_x[0] = evaluate_i_x_again(istart, x, squared_norm_of_x, true);
int i_max = istart + k_xi_x.length();
for (int i = istart + 1; i < i_max; i++) {
k_xi_x[i] = evaluate_i_x_again(i, x, squared_norm_of_x);
}
}

| void PLearn::Kernel::evaluate_all_x_i | ( | const Vec & | x, |
| const Vec & | k_x_xi, | ||
| real | squared_norm_of_x = -1, |
||
| int | istart = 0 |
||
| ) | const [virtual] |
Fill k_x_xi with K(x, x_i), for all i from istart to istart + k_x_xi.length() - 1.
Definition at line 315 of file Kernel.cc.
References evaluate_x_i_again(), i, and PLearn::TVec< T >::length().
{
k_x_xi[0] = evaluate_x_i_again(x, istart, squared_norm_of_x, true);
int i_max = istart + k_x_xi.length();
for (int i = istart + 1; i < i_max; i++) {
k_x_xi[i] = evaluate_x_i_again(x, i, squared_norm_of_x);
}
}

returns evaluate(data(i),data(j))
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::CosKernel, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::GaussianKernel, PLearn::GeodesicDistanceKernel, PLearn::LLEKernel, PLearn::ManifoldParzenKernel, PLearn::PolynomialKernel, PLearn::PrecomputedKernel, PLearn::ReconstructionWeightsKernel, PLearn::SourceKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, and PLearn::WeightedDistance.
Definition at line 221 of file Kernel.cc.
References data, data_inputsize, evaluate(), evaluate_xi, evaluate_xj, PLearn::VMat::getSubRow(), lock_xi, lock_xj, and PLearn::TVec< T >::resize().
Referenced by computeGramMatrix(), PLearn::PLearnerDiagonalKernel::computeGramMatrix(), computePartialGramMatrix(), computeSparseGramMatrix(), PLearn::GaussianKernel::evaluate_i_j(), and PLearn::DistanceKernel::evaluate_i_j().
{
static real result;
if (lock_xi || lock_xj) {
// This should not happen often, but you never know...
Vec xi(data_inputsize);
Vec xj(data_inputsize);
data->getSubRow(i, 0, xi);
data->getSubRow(j, 0, xj);
return evaluate(xi, xj);
} else {
lock_xi = true;
lock_xj = true;
evaluate_xi.resize(data_inputsize);
evaluate_xj.resize(data_inputsize);
data->getSubRow(i, 0, evaluate_xi);
data->getSubRow(j, 0, evaluate_xj);
result = evaluate(evaluate_xi, evaluate_xj);
lock_xi = false;
lock_xj = false;
return result;
}
}
| real PLearn::Kernel::evaluate_i_x | ( | int | i, |
| const Vec & | x, | ||
| real | squared_norm_of_x = -1 |
||
| ) | const [virtual] |
Return evaluate(data(i),x).
[squared_norm_of_x is just a hint that may allow to speed up computation if it is already known, but it's optional]
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::GaussianKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::LLEKernel, PLearn::PolynomialKernel, PLearn::PrecomputedKernel, PLearn::ReconstructionWeightsKernel, PLearn::SourceKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, and PLearn::VMatKernel.
Definition at line 248 of file Kernel.cc.
References data, data_inputsize, evaluate(), evaluate_xi, PLearn::VMat::getSubRow(), lock_xi, and PLearn::TVec< T >::resize().
Referenced by PLearn::GaussianKernel::evaluate_i_x(), evaluate_i_x_again(), and evaluate_x_i().
{
static real result;
if (lock_xi) {
Vec xi(data_inputsize);
data->getSubRow(i, 0, xi);
return evaluate(xi, x);
} else {
lock_xi = true;
evaluate_xi.resize(data_inputsize);
data->getSubRow(i, 0, evaluate_xi);
result = evaluate(evaluate_xi, x);
lock_xi = false;
return result;
}
}

| real PLearn::Kernel::evaluate_i_x_again | ( | int | i, |
| const Vec & | x, | ||
| real | squared_norm_of_x = -1, |
||
| bool | first_time = false |
||
| ) | const [virtual] |
Return evaluate(data(i),x), where x is the same as in the precedent call to this same function (except if 'first_time' is true).
This can be used to speed up successive computations of K(x_i, x) (default version just calls evaluate_i_x).
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::DivisiveNormalizationKernel, PLearn::GeodesicDistanceKernel, PLearn::LLEKernel, and PLearn::ThresholdedKernel.
Definition at line 290 of file Kernel.cc.
References evaluate_i_x().
Referenced by evaluate_all_i_x().
{
return evaluate_i_x(i, x, squared_norm_of_x);
}

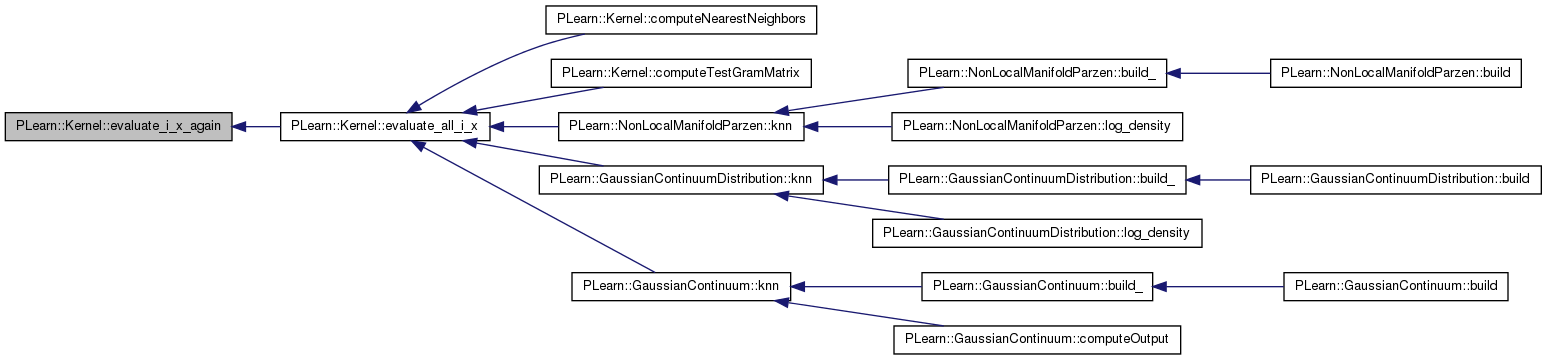
| real PLearn::Kernel::evaluate_x_i | ( | const Vec & | x, |
| int | i, | ||
| real | squared_norm_of_x = -1 |
||
| ) | const [virtual] |
returns evaluate(x,data(i)) [default version calls evaluate_i_x if kernel is_symmetric]
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::GaussianKernel, PLearn::PolynomialKernel, PLearn::PrecomputedKernel, PLearn::ReconstructionWeightsKernel, PLearn::SourceKernel, PLearn::ThresholdedKernel, and PLearn::VMatKernel.
Definition at line 267 of file Kernel.cc.
References data, data_inputsize, evaluate(), evaluate_i_x(), evaluate_xi, PLearn::VMat::getSubRow(), is_symmetric, lock_xi, and PLearn::TVec< T >::resize().
Referenced by PLearn::GaussianKernel::evaluate_x_i(), and evaluate_x_i_again().
{
static real result;
if(is_symmetric)
return evaluate_i_x(i,x,squared_norm_of_x);
else {
if (lock_xi) {
Vec xi(data_inputsize);
data->getSubRow(i, 0, xi);
return evaluate(x, xi);
} else {
lock_xi = true;
evaluate_xi.resize(data_inputsize);
data->getSubRow(i, 0, evaluate_xi);
result = evaluate(x, evaluate_xi);
lock_xi = false;
return result;
}
}
}
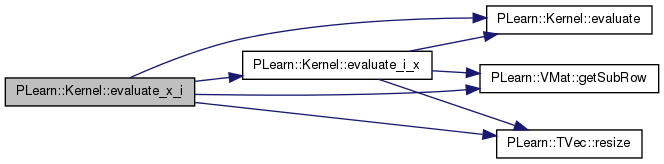

| real PLearn::Kernel::evaluate_x_i_again | ( | const Vec & | x, |
| int | i, | ||
| real | squared_norm_of_x = -1, |
||
| bool | first_time = false |
||
| ) | const [virtual] |
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::DivisiveNormalizationKernel, PLearn::ReconstructionWeightsKernel, and PLearn::ThresholdedKernel.
Definition at line 297 of file Kernel.cc.
References evaluate_x_i().
Referenced by evaluate_all_x_i().
{
return evaluate_x_i(x, i, squared_norm_of_x);
}


| VMat PLearn::Kernel::getData | ( | ) | [inline] |
| Vec PLearn::Kernel::getParameters | ( | ) | const [virtual] |
default version returns an empty Vec
Reimplemented in PLearn::SourceKernel.
Definition at line 639 of file Kernel.cc.
{ return Vec(); }
| bool PLearn::Kernel::hasData | ( | ) |
Return true iif there is a data matrix set for this kernel.
Definition at line 645 of file Kernel.cc.
References data, and PLearn::PP< T >::isNotNull().
{
return data.isNotNull();
}

Return true iff the point x is in the kernel dataset.
If provided, i will be filled with the index of the point if it is in the dataset, and with -1 otherwise.
Definition at line 326 of file Kernel.cc.
References data.
Referenced by PLearn::LLEKernel::evaluate(), PLearn::ReconstructionWeightsKernel::evaluate(), PLearn::ReconstructionWeightsKernel::evaluate_i_x(), and PLearn::LLEKernel::evaluate_i_x_again().

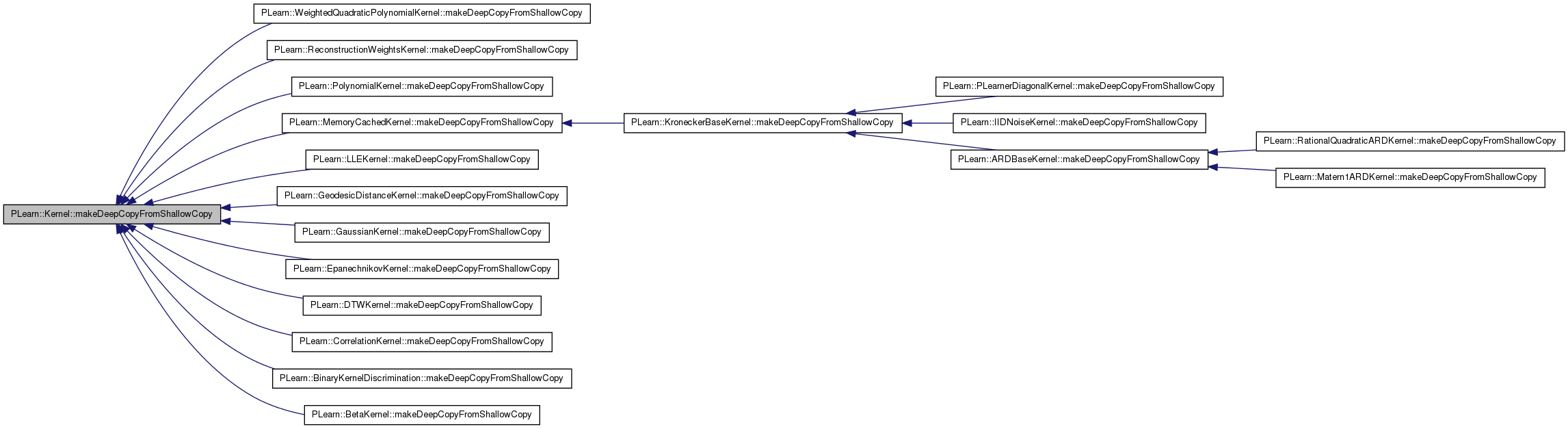
| void PLearn::Kernel::makeDeepCopyFromShallowCopy | ( | CopiesMap & | copies | ) | [virtual] |
Does the necessary operations to transform a shallow copy (this) into a deep copy by deep-copying all the members that need to be.
This needs to be overridden by every class that adds "complex" data members to the class, such as Vec, Mat, PP<Something>, etc. Typical implementation:
void CLASS_OF_THIS::makeDeepCopyFromShallowCopy(CopiesMap& copies) { inherited::makeDeepCopyFromShallowCopy(copies); deepCopyField(complex_data_member1, copies); deepCopyField(complex_data_member2, copies); ... }
| copies | A map used by the deep-copy mechanism to keep track of already-copied objects. |
Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::CorrelationKernel, PLearn::DivisiveNormalizationKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::GaussianKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::NegKernel, PLearn::NeuralNetworkARDKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PrecomputedKernel, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::ScaledLaplacianKernel, PLearn::SelectedOutputCostFunction, PLearn::SourceKernel, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedQuadraticPolynomialKernel, and PLearn::BinaryKernelDiscrimination.
Definition at line 164 of file Kernel.cc.
References data, PLearn::deepCopyField(), evaluate_xi, evaluate_xj, gram_matrix, k_xi_x, PLearn::Object::makeDeepCopyFromShallowCopy(), sparse_gram_matrix, and specify_dataset.
Referenced by PLearn::WeightedQuadraticPolynomialKernel::makeDeepCopyFromShallowCopy(), PLearn::ReconstructionWeightsKernel::makeDeepCopyFromShallowCopy(), PLearn::PolynomialKernel::makeDeepCopyFromShallowCopy(), PLearn::MemoryCachedKernel::makeDeepCopyFromShallowCopy(), PLearn::LLEKernel::makeDeepCopyFromShallowCopy(), PLearn::GeodesicDistanceKernel::makeDeepCopyFromShallowCopy(), PLearn::GaussianKernel::makeDeepCopyFromShallowCopy(), PLearn::EpanechnikovKernel::makeDeepCopyFromShallowCopy(), PLearn::DTWKernel::makeDeepCopyFromShallowCopy(), PLearn::CorrelationKernel::makeDeepCopyFromShallowCopy(), PLearn::BinaryKernelDiscrimination::makeDeepCopyFromShallowCopy(), and PLearn::BetaKernel::makeDeepCopyFromShallowCopy().
{
inherited::makeDeepCopyFromShallowCopy(copies);
deepCopyField(evaluate_xi, copies);
deepCopyField(evaluate_xj, copies);
deepCopyField(k_xi_x, copies);
deepCopyField(data, copies);
deepCopyField(gram_matrix, copies);
deepCopyField(sparse_gram_matrix, copies);
deepCopyField(specify_dataset, copies);
}

| int PLearn::Kernel::nExamples | ( | ) | const [inline] |
Return n_examples.
Definition at line 129 of file Kernel.h.
Referenced by computeGramMatrixDerivative(), and PLearn::IIDNoiseKernel::computeGramMatrixDerivative().
{
return n_examples;
}
| Mat PLearn::Kernel::returnComputedGramMatrix | ( | ) | const [virtual] |
Definition at line 408 of file Kernel.cc.
References computeGramMatrix(), data, PLearn::VMat::length(), and PLERROR.
Referenced by declareMethods().
{
if (!data)
PLERROR("Kernel::returnComputedGramMatrix should be called only after setDataForKernelMatrix");
int l=data.length();
Mat K(l,l);
computeGramMatrix(K);
return K;
}

| void PLearn::Kernel::setDataForKernelMatrix | ( | VMat | the_data | ) | [virtual] |
** Subclasses may override these methods to provide efficient kernel matrix access **
This method sets the data VMat that will be used to define the kernel matrix. It may precompute values from this that may later accelerate the evaluation of a kernel matrix element
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::CorrelationKernel, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::GaussianKernel, PLearn::GeodesicDistanceKernel, PLearn::LLEKernel, PLearn::ManifoldParzenKernel, PLearn::MemoryCachedKernel, PLearn::NonLocalManifoldParzenKernel, PLearn::PrecomputedKernel, PLearn::ReconstructionWeightsKernel, PLearn::SourceKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, and PLearn::WeightedDistance.
Definition at line 185 of file Kernel.cc.
References data, data_inputsize, gram_matrix_is_cached, PLearn::VMat::length(), n_examples, sparse_gram_matrix_is_cached, and PLearn::VMat::width().
Referenced by build_(), declareMethods(), PLearn::GaussianProcessNLLVariable::fbpropFragments(), PLearn::GaussianKernel::setDataForKernelMatrix(), PLearn::LLEKernel::setDataForKernelMatrix(), PLearn::ReconstructionWeightsKernel::setDataForKernelMatrix(), PLearn::GeodesicDistanceKernel::setDataForKernelMatrix(), PLearn::PrecomputedKernel::setDataForKernelMatrix(), PLearn::MemoryCachedKernel::setDataForKernelMatrix(), PLearn::DistanceKernel::setDataForKernelMatrix(), and PLearn::CorrelationKernel::setDataForKernelMatrix().
{
data = the_data;
if (data) {
data_inputsize = data->inputsize();
if (data_inputsize == -1) {
// Default value when no inputsize is specified.
data_inputsize = data->width();
}
n_examples = data->length();
} else {
data_inputsize = 0;
n_examples = 0;
}
gram_matrix_is_cached = false;
sparse_gram_matrix_is_cached = false;
}

| void PLearn::Kernel::setParameters | ( | Vec | paramvec | ) | [virtual] |
** Subclasses may override these methods ** They provide a generic way to set and retrieve kernel parameters
default version produces an error
Reimplemented in PLearn::CompactVMatrixGaussianKernel, PLearn::GaussianKernel, and PLearn::SourceKernel.
Definition at line 633 of file Kernel.cc.
References PLERROR.
{ PLERROR("setParameters(Vec paramvec) not implemented for this kernel"); }
| real PLearn::Kernel::test | ( | VMat | d, |
| real | threshold, | ||
| real | sameness_below_threshold, | ||
| real | sameness_above_threshold | ||
| ) | const |
Definition at line 758 of file Kernel.cc.
References d, evaluate(), PLearn::fast_exact_is_equal(), i, PLearn::TVec< T >::length(), PLearn::VMat::length(), PLearn::TVec< T >::subVec(), and PLearn::VMat::width().
{
int nerrors = 0;
int inputsize = (d->width()-1)/2;
for(int i=0; i<d->length(); i++)
{
Vec inputs = d(i);
Vec input1 = inputs.subVec(0,inputsize);
Vec input2 = inputs.subVec(inputsize,inputsize);
real sameness = inputs[inputs.length()-1];
real kernelvalue = evaluate(input1,input2);
cerr << "[" << kernelvalue << " " << sameness << "]\n";
if(kernelvalue<threshold)
{
if(fast_exact_is_equal(sameness, sameness_above_threshold))
nerrors++;
}
else // kernelvalue>=threshold
{
if(fast_exact_is_equal(sameness, sameness_below_threshold))
nerrors++;
}
}
return real(nerrors)/d->length();
}
| void PLearn::Kernel::train | ( | VMat | data | ) | [virtual] |
Subclasses may override this method for kernels that can be trained on a dataset prior to being used (e.g.
a Mahalanobis distance which could learn the empirical covariance) Note: in general only the input and weight part of the vmat are used
Reimplemented in PLearn::PartsDistanceKernel.
Definition at line 179 of file Kernel.cc.
{}
Reimplemented from PLearn::Object.
Reimplemented in PLearn::AdditiveNormalizationKernel, PLearn::ARDBaseKernel, PLearn::BetaKernel, PLearn::ClassDistanceProportionCostFunction, PLearn::ClassErrorCostFunction, PLearn::ClassMarginCostFunction, PLearn::CompactVMatrixGaussianKernel, PLearn::CompactVMatrixPolynomialKernel, PLearn::ConvexBasisKernel, PLearn::CorrelationKernel, PLearn::CosKernel, PLearn::DifferenceKernel, PLearn::DirectNegativeCostFunction, PLearn::DistanceKernel, PLearn::DivisiveNormalizationKernel, PLearn::DotProductKernel, PLearn::DTWKernel, PLearn::EpanechnikovKernel, PLearn::PartsDistanceKernel, PLearn::GaussianDensityKernel, PLearn::GaussianKernel, PLearn::GeneralizedDistanceRBFKernel, PLearn::GeodesicDistanceKernel, PLearn::IIDNoiseKernel, PLearn::KroneckerBaseKernel, PLearn::LaplacianKernel, PLearn::LiftBinaryCostFunction, PLearn::LinearARDKernel, PLearn::LLEKernel, PLearn::LogOfGaussianDensityKernel, PLearn::ManifoldParzenKernel, PLearn::Matern1ARDKernel, PLearn::MemoryCachedKernel, PLearn::MulticlassErrorCostFunction, PLearn::NegKernel, PLearn::NegLogProbCostFunction, PLearn::NegOutputCostFunction, PLearn::NeuralNetworkARDKernel, PLearn::NonLocalManifoldParzenKernel, PLearn::NormalizedDotProductKernel, PLearn::PLearnerDiagonalKernel, PLearn::PolynomialKernel, PLearn::PowDistanceKernel, PLearn::PrecomputedKernel, PLearn::PricingTransactionPairProfitFunction, PLearn::QuadraticUtilityCostFunction, PLearn::RationalQuadraticARDKernel, PLearn::ReconstructionWeightsKernel, PLearn::ScaledGaussianKernel, PLearn::ScaledGeneralizedDistanceRBFKernel, PLearn::ScaledLaplacianKernel, PLearn::SelectedOutputCostFunction, PLearn::SigmoidalKernel, PLearn::SigmoidPrimitiveKernel, PLearn::SourceKernel, PLearn::SquaredErrorCostFunction, PLearn::SquaredExponentialARDKernel, PLearn::SummationKernel, PLearn::ThresholdedKernel, PLearn::VMatKernel, PLearn::WeightedCostFunction, PLearn::WeightedQuadraticPolynomialKernel, PLearn::WeightedDistance, and PLearn::BinaryKernelDiscrimination.
Build options.
Definition at line 84 of file Kernel.h.
Referenced by computeGramMatrix(), PLearn::ThresholdedKernel::computeGramMatrix(), PLearn::IIDNoiseKernel::computeGramMatrix(), PLearn::Matern1ARDKernel::computeGramMatrix(), PLearn::PLearnerDiagonalKernel::computeGramMatrix(), PLearn::RationalQuadraticARDKernel::computeGramMatrix(), computeGramMatrixDerivative(), PLearn::MemoryCachedKernel::computeGramMatrixNV(), computeSparseGramMatrix(), declareOptions(), PLearn::MemoryCachedKernel::MemoryCachedKernel(), and PLearn::ThresholdedKernel::setDataForKernelMatrix().
VMat PLearn::Kernel::data [protected] |
data for kernel matrix, which will be used for calls to evaluate_i_j and the like
Definition at line 68 of file Kernel.h.
Referenced by addDataForKernelMatrix(), PLearn::GaussianKernel::addDataForKernelMatrix(), PLearn::RationalQuadraticARDKernel::computeGramMatrix(), PLearn::Matern1ARDKernel::computeGramMatrix(), PLearn::KroneckerBaseKernel::computeGramMatrix(), computeGramMatrix(), PLearn::IIDNoiseKernel::computeGramMatrix(), computeGramMatrixDerivative(), PLearn::IIDNoiseKernel::computeGramMatrixDerivative(), PLearn::RationalQuadraticARDKernel::computeGramMatrixDerivIspAlpha(), PLearn::RationalQuadraticARDKernel::computeGramMatrixDerivIspInputSigma(), PLearn::Matern1ARDKernel::computeGramMatrixDerivIspInputSigma(), PLearn::RationalQuadraticARDKernel::computeGramMatrixDerivIspSignalSigma(), PLearn::PLearnerDiagonalKernel::computeGramMatrixDerivIspSignalSigma(), PLearn::Matern1ARDKernel::computeGramMatrixDerivIspSignalSigma(), PLearn::IIDNoiseKernel::computeGramMatrixDerivKronecker(), PLearn::MemoryCachedKernel::computeGramMatrixNV(), computePartialGramMatrix(), computeSparseGramMatrix(), computeTestGramMatrix(), PLearn::ReconstructionWeightsKernel::computeWeights(), PLearn::MemoryCachedKernel::dataRow(), PLearn::RationalQuadraticARDKernel::evaluate_all_i_x(), PLearn::IIDNoiseKernel::evaluate_all_i_x(), PLearn::PolynomialKernel::evaluate_i_j(), evaluate_i_j(), PLearn::GaussianKernel::evaluate_i_j(), PLearn::DistanceKernel::evaluate_i_j(), PLearn::PolynomialKernel::evaluate_i_x(), evaluate_i_x(), PLearn::GaussianKernel::evaluate_i_x(), PLearn::PolynomialKernel::evaluate_x_i(), evaluate_x_i(), PLearn::GaussianKernel::evaluate_x_i(), PLearn::MemoryCachedKernel::evaluateAllIXNV(), hasData(), isInData(), makeDeepCopyFromShallowCopy(), returnComputedGramMatrix(), setDataForKernelMatrix(), PLearn::GaussianKernel::setDataForKernelMatrix(), PLearn::DivisiveNormalizationKernel::setDataForKernelMatrix(), PLearn::DistanceKernel::setDataForKernelMatrix(), and PLearn::AdditiveNormalizationKernel::setDataForKernelMatrix().
int PLearn::Kernel::data_inputsize [protected] |
Definition at line 69 of file Kernel.h.
Referenced by PLearn::ReconstructionWeightsKernel::computeWeights(), declareOptions(), PLearn::GaussianKernel::evaluate_i_j(), PLearn::DistanceKernel::evaluate_i_j(), evaluate_i_j(), evaluate_i_x(), evaluate_x_i(), PLearn::GaussianKernel::setDataForKernelMatrix(), setDataForKernelMatrix(), and PLearn::DistanceKernel::setDataForKernelMatrix().
Vec PLearn::Kernel::evaluate_xi [mutable, private] |
Used to store data to save memory allocation.
Definition at line 61 of file Kernel.h.
Referenced by evaluate_i_j(), evaluate_i_x(), evaluate_x_i(), and makeDeepCopyFromShallowCopy().
Vec PLearn::Kernel::evaluate_xj [mutable, private] |
Definition at line 61 of file Kernel.h.
Referenced by evaluate_i_j(), and makeDeepCopyFromShallowCopy().
Mat PLearn::Kernel::gram_matrix [mutable, protected] |
Cached Gram matrix.
Definition at line 70 of file Kernel.h.
Referenced by computeGramMatrix(), PLearn::ThresholdedKernel::computeGramMatrix(), PLearn::IIDNoiseKernel::computeGramMatrix(), PLearn::Matern1ARDKernel::computeGramMatrix(), PLearn::PLearnerDiagonalKernel::computeGramMatrix(), PLearn::RationalQuadraticARDKernel::computeGramMatrix(), PLearn::RationalQuadraticARDKernel::computeGramMatrixDerivIspAlpha(), PLearn::Matern1ARDKernel::computeGramMatrixDerivIspInputSigma(), PLearn::PLearnerDiagonalKernel::computeGramMatrixDerivIspSignalSigma(), PLearn::Matern1ARDKernel::computeGramMatrixDerivIspSignalSigma(), PLearn::RationalQuadraticARDKernel::computeGramMatrixDerivIspSignalSigma(), PLearn::IIDNoiseKernel::computeGramMatrixDerivKronecker(), PLearn::MemoryCachedKernel::computeGramMatrixNV(), computeSparseGramMatrix(), makeDeepCopyFromShallowCopy(), and PLearn::ThresholdedKernel::setDataForKernelMatrix().
bool PLearn::Kernel::gram_matrix_is_cached [mutable, protected] |
Definition at line 72 of file Kernel.h.
Referenced by computeGramMatrix(), PLearn::ThresholdedKernel::computeGramMatrix(), PLearn::IIDNoiseKernel::computeGramMatrix(), PLearn::Matern1ARDKernel::computeGramMatrix(), PLearn::PLearnerDiagonalKernel::computeGramMatrix(), PLearn::RationalQuadraticARDKernel::computeGramMatrix(), PLearn::MemoryCachedKernel::computeGramMatrixNV(), computeSparseGramMatrix(), PLearn::ThresholdedKernel::setDataForKernelMatrix(), and setDataForKernelMatrix().
Definition at line 85 of file Kernel.h.
Referenced by apply(), PLearn::DivisiveNormalizationKernel::computeAverage(), PLearn::AdditiveNormalizationKernel::computeAverage(), computeGramMatrix(), PLearn::KroneckerBaseKernel::computeGramMatrix(), PLearn::IIDNoiseKernel::computeGramMatrix(), PLearn::MemoryCachedKernel::computeGramMatrixNV(), computePartialGramMatrix(), computeSparseGramMatrix(), declareOptions(), evaluate_x_i(), PLearn::GaussianProcessNLLVariable::fbpropFragments(), PLearn::ReconstructionWeightsKernel::ReconstructionWeightsKernel(), PLearn::DivisiveNormalizationKernel::setDataForKernelMatrix(), and PLearn::AdditiveNormalizationKernel::setDataForKernelMatrix().
Vec PLearn::Kernel::k_xi_x [mutable, private] |
Definition at line 61 of file Kernel.h.
Referenced by computeNearestNeighbors(), PLearn::PLearnerDiagonalKernel::evaluate_all_i_x(), PLearn::Matern1ARDKernel::evaluate_all_i_x(), and makeDeepCopyFromShallowCopy().
bool PLearn::Kernel::lock_k_xi_x [mutable, private] |
Definition at line 64 of file Kernel.h.
Referenced by computeNearestNeighbors().
bool PLearn::Kernel::lock_xi [mutable, private] |
Used to make sure we do not accidentally overwrite some global data.
Definition at line 64 of file Kernel.h.
Referenced by evaluate_i_j(), evaluate_i_x(), and evaluate_x_i().
bool PLearn::Kernel::lock_xj [mutable, private] |
Definition at line 64 of file Kernel.h.
Referenced by evaluate_i_j().
int PLearn::Kernel::n_examples [protected] |
Definition at line 74 of file Kernel.h.
Referenced by PLearn::DivisiveNormalizationKernel::computeAverage(), PLearn::AdditiveNormalizationKernel::computeAverage(), PLearn::LLEKernel::computeGramMatrix(), PLearn::ReconstructionWeightsKernel::computeLLEMatrix(), computeNearestNeighbors(), PLearn::ReconstructionWeightsKernel::computeWeights(), declareOptions(), PLearn::ThresholdedKernel::evaluate_random_k_x_i(), setDataForKernelMatrix(), and PLearn::GeodesicDistanceKernel::setDataForKernelMatrix().
Definition at line 86 of file Kernel.h.
Referenced by apply(), PLearn::RemoveDuplicateVMatrix::build_(), PLearn::ReconstructionWeightsKernel::build_(), PLearn::LLEKernel::build_(), PLearn::KNNVMatrix::build_(), PLearn::Isomap::build_(), computeGramMatrix(), PLearn::MemoryCachedKernel::computeGramMatrixNV(), PLearn::ReconstructionWeightsKernel::computeLLEMatrix(), computePartialGramMatrix(), computeSparseGramMatrix(), computeTestGramMatrix(), PLearn::ReconstructionWeightsKernel::computeWeights(), declareOptions(), PLearn::ThresholdedKernel::setDataForKernelMatrix(), PLearn::GeodesicDistanceKernel::setDataForKernelMatrix(), and PLearn::ThresholdedKernel::thresholdGramMatrix().
TVec<Mat> PLearn::Kernel::sparse_gram_matrix [mutable, protected] |
Cached sparse Gram matrix.
Definition at line 71 of file Kernel.h.
Referenced by computeSparseGramMatrix(), makeDeepCopyFromShallowCopy(), and PLearn::ThresholdedKernel::setDataForKernelMatrix().
bool PLearn::Kernel::sparse_gram_matrix_is_cached [mutable, protected] |
Definition at line 73 of file Kernel.h.
Referenced by computeSparseGramMatrix(), PLearn::ThresholdedKernel::setDataForKernelMatrix(), and setDataForKernelMatrix().
Definition at line 87 of file Kernel.h.
Referenced by PLearn::ReconstructionWeightsKernel::build_(), PLearn::LLEKernel::build_(), build_(), declareOptions(), and makeDeepCopyFromShallowCopy().
 1.7.4
1.7.4