|
PLearn 0.1
|
|
PLearn 0.1
|
#include <GeodesicDistanceKernel.h>
Public Member Functions | |
| GeodesicDistanceKernel () | |
| Default constructor. | |
| GeodesicDistanceKernel (Ker the_distance_kernel, int the_knn=10, const PPath &the_geodesic_file="", bool the_pow_distance=false, const string &the_method="floyd", bool call_build_=true) | |
| Convenient constructor. | |
| virtual void | build () |
| Simply calls inherited::build() then build_(). | |
| virtual void | makeDeepCopyFromShallowCopy (CopiesMap &copies) |
| Transforms a shallow copy into a deep copy. | |
| virtual string | classname () const |
| virtual OptionList & | getOptionList () const |
| virtual OptionMap & | getOptionMap () const |
| virtual RemoteMethodMap & | getRemoteMethodMap () const |
| virtual GeodesicDistanceKernel * | deepCopy (CopiesMap &copies) const |
| int | computeNearestGeodesicNeighbour (int i, const Mat &distances_xi_x_sorted, real *dist_i=0) const |
| Return the index j of the data point which satisfies: 1. | |
| real | computeShortestDistance (int i, const Mat &distances_xi_x_sorted) const |
| Return the shortest (geodesic) distance to i from a point x whose (non-geodesic) distance to its knn nearest neighbors in the training set is given by the matrix 'distances_xi_x_sorted', whose first column should contain the sorted distances, and whose second column should contain the corresponding indices. | |
| virtual real | evaluate (const Vec &x1, const Vec &x2) const |
| Compute K(x1,x2). | |
| virtual real | evaluate_i_j (int i, int j) const |
| returns evaluate(data(i),data(j)) | |
| virtual real | evaluate_i_x (int i, const Vec &x, real squared_norm_of_x=-1) const |
| Return evaluate(data(i),x). | |
| virtual real | evaluate_i_x_again (int i, const Vec &x, real squared_norm_of_x=-1, bool first_time=false) const |
| Return evaluate(data(i),x), where x is the same as in the precedent call to this same function (except if 'first_time' is true). | |
| virtual real | evaluate_i_x_from_distances (int i, const Mat &distances_xi_x_sorted) const |
| Evaluate K(x_i,x) where x is not given explicitly, but only by the (sorted and non-geodesic) distances to all training points. | |
| virtual void | setDataForKernelMatrix (VMat the_data) |
| Overridden to precompute inter-points geodesic distance. | |
Static Public Member Functions | |
| static string | _classname_ () |
| static OptionList & | _getOptionList_ () |
| static RemoteMethodMap & | _getRemoteMethodMap_ () |
| static Object * | _new_instance_for_typemap_ () |
| static bool | _isa_ (const Object *o) |
| static void | _static_initialize_ () |
| static const PPath & | declaringFile () |
Public Attributes | |
| Ker | distance_kernel |
| PPath | geodesic_file |
| int | knn |
| bool | pow_distance |
| string | shortest_algo |
| VMat | geo_distances |
Static Public Attributes | |
| static StaticInitializer | _static_initializer_ |
Static Protected Member Functions | |
| static void | declareOptions (OptionList &ol) |
| Declares this class' options. | |
Private Types | |
| typedef Kernel | inherited |
Private Member Functions | |
| void | build_ () |
| This does the actual building. | |
Private Attributes | |
| Mat | dist_xi_x_sorted1 |
| Used to store data and save memory allocation. | |
| Mat | dist_xi_x_sorted2 |
| Mat | dist_xi_x_sorted |
Definition at line 52 of file GeodesicDistanceKernel.h.
typedef Kernel PLearn::GeodesicDistanceKernel::inherited [private] |
Reimplemented from PLearn::Kernel.
Definition at line 57 of file GeodesicDistanceKernel.h.
| PLearn::GeodesicDistanceKernel::GeodesicDistanceKernel | ( | ) |
Default constructor.
Definition at line 54 of file GeodesicDistanceKernel.cc.
References distance_kernel.
: geodesic_file(""), knn(10), pow_distance(false), shortest_algo("floyd") { distance_kernel = new DistanceKernel(2); }
| PLearn::GeodesicDistanceKernel::GeodesicDistanceKernel | ( | Ker | the_distance_kernel, |
| int | the_knn = 10, |
||
| const PPath & | the_geodesic_file = "", |
||
| bool | the_pow_distance = false, |
||
| const string & | the_method = "floyd", |
||
| bool | call_build_ = true |
||
| ) |
Convenient constructor.
Definition at line 63 of file GeodesicDistanceKernel.cc.
References build_(), and distance_kernel.
:
inherited(true, call_build_),
geodesic_file(the_geodesic_file),
knn(the_knn),
pow_distance(the_pow_distance),
shortest_algo(the_method)
{
distance_kernel = the_distance_kernel;
if (call_build_)
build_();
}

| string PLearn::GeodesicDistanceKernel::_classname_ | ( | ) | [static] |
Reimplemented from PLearn::Kernel.
Definition at line 82 of file GeodesicDistanceKernel.cc.
| OptionList & PLearn::GeodesicDistanceKernel::_getOptionList_ | ( | ) | [static] |
Reimplemented from PLearn::Kernel.
Definition at line 82 of file GeodesicDistanceKernel.cc.
| RemoteMethodMap & PLearn::GeodesicDistanceKernel::_getRemoteMethodMap_ | ( | ) | [static] |
Reimplemented from PLearn::Kernel.
Definition at line 82 of file GeodesicDistanceKernel.cc.
Reimplemented from PLearn::Kernel.
Definition at line 82 of file GeodesicDistanceKernel.cc.
| Object * PLearn::GeodesicDistanceKernel::_new_instance_for_typemap_ | ( | ) | [static] |
Reimplemented from PLearn::Object.
Definition at line 82 of file GeodesicDistanceKernel.cc.
| StaticInitializer GeodesicDistanceKernel::_static_initializer_ & PLearn::GeodesicDistanceKernel::_static_initialize_ | ( | ) | [static] |
Reimplemented from PLearn::Kernel.
Definition at line 82 of file GeodesicDistanceKernel.cc.
| void PLearn::GeodesicDistanceKernel::build | ( | ) | [virtual] |
Simply calls inherited::build() then build_().
Reimplemented from PLearn::Kernel.
Definition at line 120 of file GeodesicDistanceKernel.cc.
References PLearn::Kernel::build(), and build_().
{
inherited::build();
build_();
}

| void PLearn::GeodesicDistanceKernel::build_ | ( | ) | [private] |
This does the actual building.
Reimplemented from PLearn::Kernel.
Definition at line 129 of file GeodesicDistanceKernel.cc.
Referenced by build(), and GeodesicDistanceKernel().
{
}

| string PLearn::GeodesicDistanceKernel::classname | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 82 of file GeodesicDistanceKernel.cc.
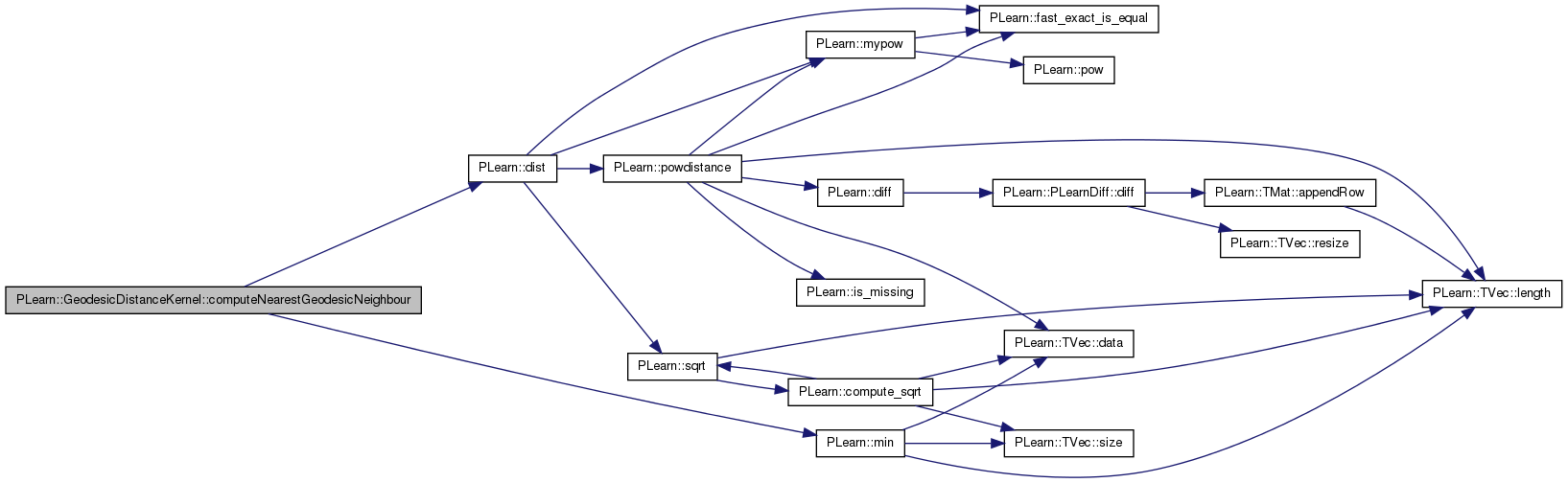
| int PLearn::GeodesicDistanceKernel::computeNearestGeodesicNeighbour | ( | int | i, |
| const Mat & | distances_xi_x_sorted, | ||
| real * | dist_i = 0 |
||
| ) | const |
Return the index j of the data point which satisfies: 1.
j is among the knn nearest neighbors of the point x from which was computed 'distances_xi_x_sorted' 2. it is such that dist(x,j) + geodesic_dist(j,x_i) is minimum If provided, the 'dist_i' parameter is filled with the geodesic distance from x to x_i.
Definition at line 136 of file GeodesicDistanceKernel.cc.
References PLearn::dist(), geo_distances, j, knn, and PLearn::min().
Referenced by computeShortestDistance().
{
real min = distances_xi_x_sorted(0,0) + geo_distances->get(i, int(distances_xi_x_sorted(0,1)));
real dist;
int indice = 0;
for (int j = 1; j < knn; j++) {
dist = distances_xi_x_sorted(j,0) + geo_distances->get(i, int(distances_xi_x_sorted(j,1)));
if (dist < min) {
min = dist;
indice = j;
}
}
if (dist_i)
*dist_i = min;
return int(distances_xi_x_sorted(indice,1));
}

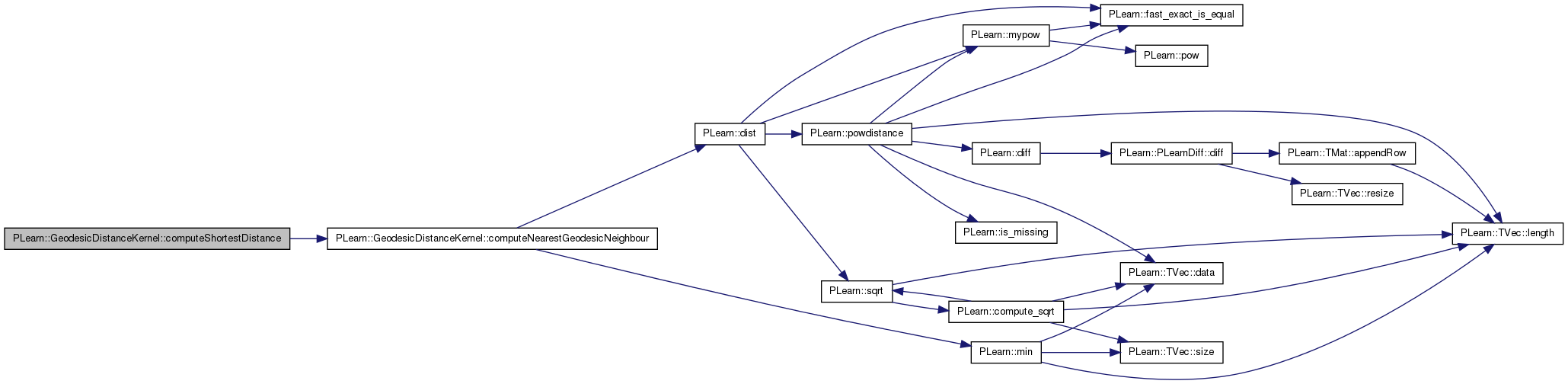
| real PLearn::GeodesicDistanceKernel::computeShortestDistance | ( | int | i, |
| const Mat & | distances_xi_x_sorted | ||
| ) | const |
Return the shortest (geodesic) distance to i from a point x whose (non-geodesic) distance to its knn nearest neighbors in the training set is given by the matrix 'distances_xi_x_sorted', whose first column should contain the sorted distances, and whose second column should contain the corresponding indices.
Definition at line 155 of file GeodesicDistanceKernel.cc.
References computeNearestGeodesicNeighbour().
Referenced by evaluate_i_x_again(), and evaluate_i_x_from_distances().
{
static real result;
computeNearestGeodesicNeighbour(i, distances_xi_x_sorted, &result);
return result;
}

| void PLearn::GeodesicDistanceKernel::declareOptions | ( | OptionList & | ol | ) | [static, protected] |
Declares this class' options.
Reimplemented from PLearn::Kernel.
Definition at line 87 of file GeodesicDistanceKernel.cc.
References PLearn::OptionBase::buildoption, PLearn::declareOption(), PLearn::Kernel::declareOptions(), distance_kernel, geo_distances, geodesic_file, knn, PLearn::OptionBase::learntoption, pow_distance, and shortest_algo.
{
// Build options.
declareOption(ol, "knn", &GeodesicDistanceKernel::knn, OptionBase::buildoption,
"The number of nearest neighbors considered.");
declareOption(ol, "distance_kernel", &GeodesicDistanceKernel::distance_kernel, OptionBase::buildoption,
"The kernel giving the distance between two points.");
declareOption(ol, "pow_distance", &GeodesicDistanceKernel::pow_distance, OptionBase::buildoption,
"If set to 1, then it will compute the squared geodesic distance.");
declareOption(ol, "geodesic_file", &GeodesicDistanceKernel::geodesic_file, OptionBase::buildoption,
"If provided, the geodesic distances will be saved in this file in binary format.");
declareOption(ol, "shortest_algo", &GeodesicDistanceKernel::shortest_algo, OptionBase::buildoption,
"The algorithm used to compute the geodesic distances:\n"
" - floyd : Floyd's algorithm\n"
" - dijkstra : Dijkstra's algorithm");
// Learnt options.
declareOption(ol, "geo_distances", &GeodesicDistanceKernel::geo_distances, OptionBase::learntoption,
"The geodesic distances between training points.");
// Now call the parent class' declareOptions
inherited::declareOptions(ol);
}

| static const PPath& PLearn::GeodesicDistanceKernel::declaringFile | ( | ) | [inline, static] |
Reimplemented from PLearn::Kernel.
Definition at line 124 of file GeodesicDistanceKernel.h.
| GeodesicDistanceKernel * PLearn::GeodesicDistanceKernel::deepCopy | ( | CopiesMap & | copies | ) | const [virtual] |
Reimplemented from PLearn::Kernel.
Definition at line 82 of file GeodesicDistanceKernel.cc.
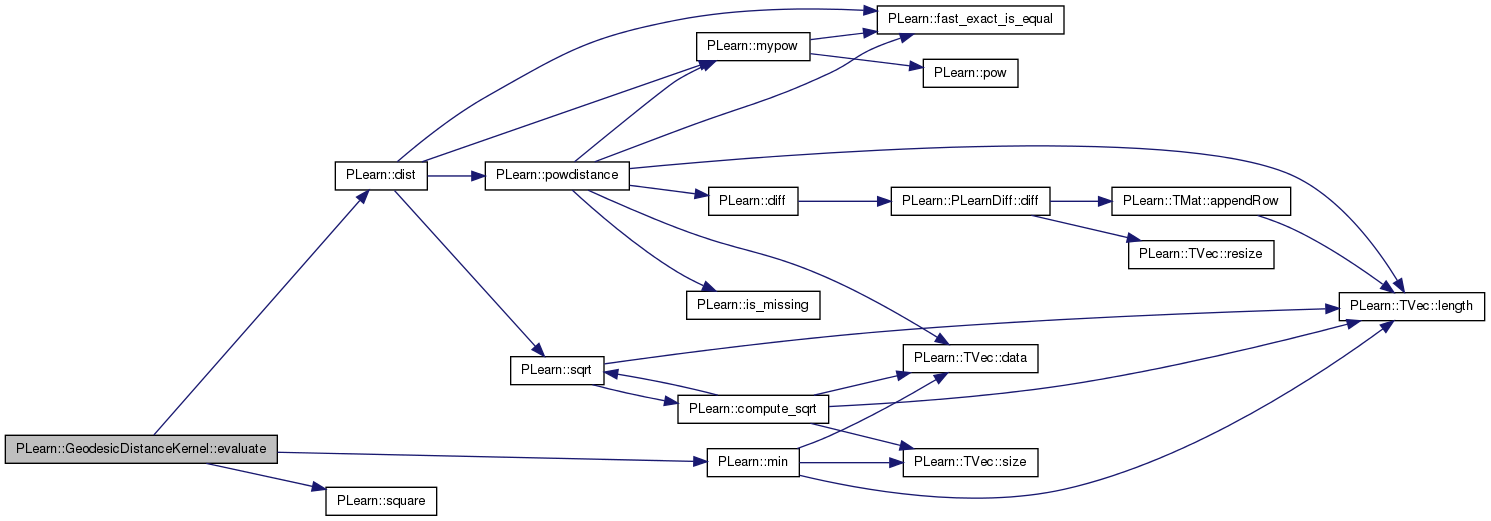
Compute K(x1,x2).
Implements PLearn::Kernel.
Definition at line 164 of file GeodesicDistanceKernel.cc.
References PLearn::dist(), dist_xi_x_sorted1, dist_xi_x_sorted2, distance_kernel, geo_distances, j, knn, PLearn::min(), pow_distance, and PLearn::square().
{
distance_kernel->computeNearestNeighbors(x1, dist_xi_x_sorted1, knn);
distance_kernel->computeNearestNeighbors(x2, dist_xi_x_sorted2, knn);
real min = REAL_MAX;
real dist;
for (int j = 0; j < knn; j++) {
for (int k = 0; k < knn; k++) {
dist = dist_xi_x_sorted1(j,0) + dist_xi_x_sorted2(k,0)
+ geo_distances->get(int(dist_xi_x_sorted1(j,1)), int(dist_xi_x_sorted2(k,1)));
if (dist < min) {
min = dist;
}
}
}
if (pow_distance) {
return square(min);
} else {
return min;
}
}
returns evaluate(data(i),data(j))
Reimplemented from PLearn::Kernel.
Definition at line 188 of file GeodesicDistanceKernel.cc.
References geo_distances, pow_distance, and PLearn::square().
{
if (pow_distance) {
return square(geo_distances->get(i,j));
} else {
return geo_distances->get(i,j);
}
}

| real PLearn::GeodesicDistanceKernel::evaluate_i_x | ( | int | i, |
| const Vec & | x, | ||
| real | squared_norm_of_x = -1 |
||
| ) | const [virtual] |
Return evaluate(data(i),x).
[squared_norm_of_x is just a hint that may allow to speed up computation if it is already known, but it's optional]
Reimplemented from PLearn::Kernel.
Definition at line 199 of file GeodesicDistanceKernel.cc.
References evaluate_i_x_again().
{
return evaluate_i_x_again(i, x, squared_norm_of_x, true);
}

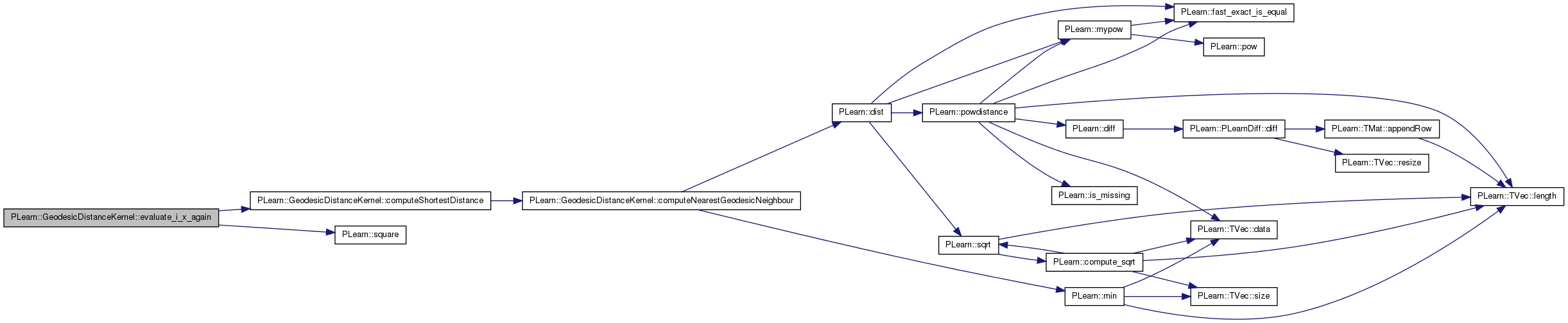
| real PLearn::GeodesicDistanceKernel::evaluate_i_x_again | ( | int | i, |
| const Vec & | x, | ||
| real | squared_norm_of_x = -1, |
||
| bool | first_time = false |
||
| ) | const [virtual] |
Return evaluate(data(i),x), where x is the same as in the precedent call to this same function (except if 'first_time' is true).
This can be used to speed up successive computations of K(x_i, x) (default version just calls evaluate_i_x).
Reimplemented from PLearn::Kernel.
Definition at line 217 of file GeodesicDistanceKernel.cc.
References computeShortestDistance(), dist_xi_x_sorted, distance_kernel, knn, pow_distance, and PLearn::square().
Referenced by evaluate_i_x().
{
if (first_time) {
distance_kernel->computeNearestNeighbors(x, dist_xi_x_sorted, knn);
}
if (pow_distance) {
return square(computeShortestDistance(i, dist_xi_x_sorted));
} else {
return computeShortestDistance(i, dist_xi_x_sorted);
}
}

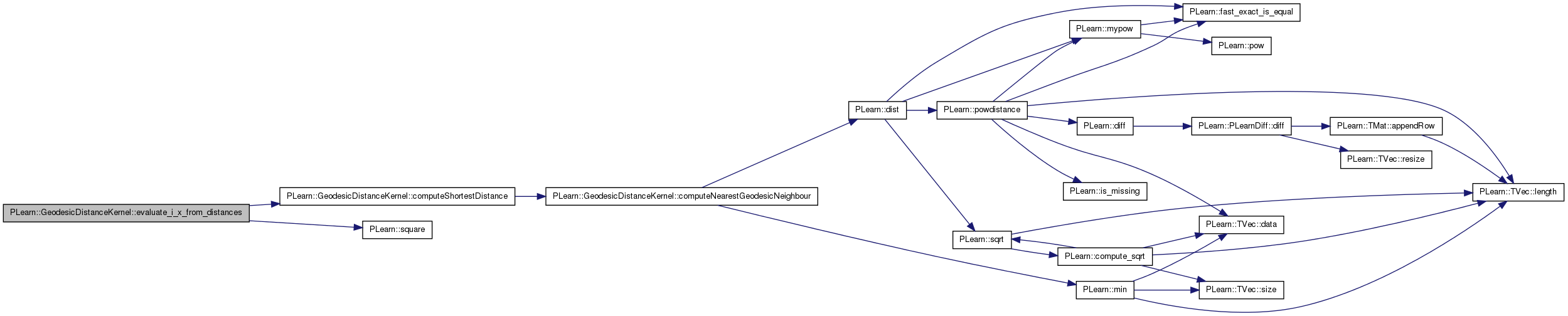
| real PLearn::GeodesicDistanceKernel::evaluate_i_x_from_distances | ( | int | i, |
| const Mat & | distances_xi_x_sorted | ||
| ) | const [virtual] |
Evaluate K(x_i,x) where x is not given explicitly, but only by the (sorted and non-geodesic) distances to all training points.
Definition at line 206 of file GeodesicDistanceKernel.cc.
References computeShortestDistance(), pow_distance, and PLearn::square().
{
if (pow_distance) {
return square(computeShortestDistance(i, distances_xi_x_sorted));
} else {
return computeShortestDistance(i, distances_xi_x_sorted);
}
}
| OptionList & PLearn::GeodesicDistanceKernel::getOptionList | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 82 of file GeodesicDistanceKernel.cc.
| OptionMap & PLearn::GeodesicDistanceKernel::getOptionMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 82 of file GeodesicDistanceKernel.cc.
| RemoteMethodMap & PLearn::GeodesicDistanceKernel::getRemoteMethodMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 82 of file GeodesicDistanceKernel.cc.
| void PLearn::GeodesicDistanceKernel::makeDeepCopyFromShallowCopy | ( | CopiesMap & | copies | ) | [virtual] |
Transforms a shallow copy into a deep copy.
Reimplemented from PLearn::Kernel.
Definition at line 231 of file GeodesicDistanceKernel.cc.
References PLearn::deepCopyField(), dist_xi_x_sorted, dist_xi_x_sorted1, dist_xi_x_sorted2, distance_kernel, geo_distances, and PLearn::Kernel::makeDeepCopyFromShallowCopy().
{
inherited::makeDeepCopyFromShallowCopy(copies);
deepCopyField(dist_xi_x_sorted1, copies);
deepCopyField(dist_xi_x_sorted2, copies);
deepCopyField(dist_xi_x_sorted, copies);
deepCopyField(distance_kernel, copies);
deepCopyField(geo_distances, copies);
}

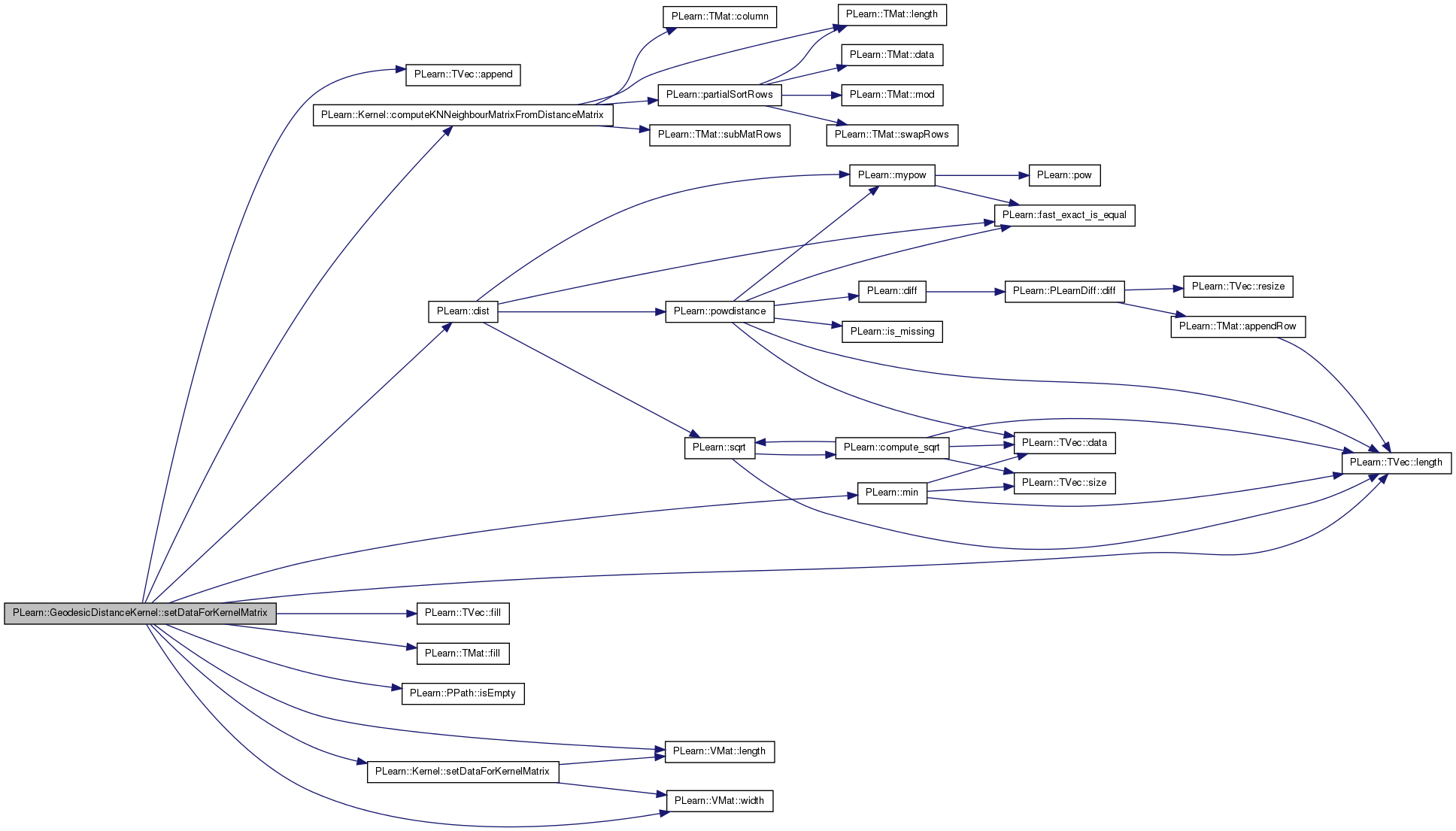
| void PLearn::GeodesicDistanceKernel::setDataForKernelMatrix | ( | VMat | the_data | ) | [virtual] |
Overridden to precompute inter-points geodesic distance.
Reimplemented from PLearn::Kernel.
Definition at line 244 of file GeodesicDistanceKernel.cc.
References PLearn::TVec< T >::append(), PLearn::Kernel::computeKNNeighbourMatrixFromDistanceMatrix(), d, PLearn::dist(), distance_kernel, PLearn::TVec< T >::fill(), PLearn::TMat< T >::fill(), geo_distances, geodesic_file, i, PLearn::PPath::isEmpty(), j, knn, PLearn::TVec< T >::length(), PLearn::VMat::length(), m, PLearn::min(), n, PLearn::Kernel::n_examples, PLERROR, PLearn::Kernel::report_progress, PLearn::Kernel::setDataForKernelMatrix(), shortest_algo, and PLearn::VMat::width().
{
inherited::setDataForKernelMatrix(the_data);
distance_kernel->setDataForKernelMatrix(the_data);
int n = n_examples;
// Check whether we have already compute the geodesic distances.
if (geo_distances && geo_distances->length() == n && geo_distances->width() == n) {
return;
}
// Compute pair distances.
Mat distances(n,n);
distance_kernel->computeGramMatrix(distances);
// Compute knn - nearest neighbors.
TMat<int> neighborhoods =
Kernel::computeKNNeighbourMatrixFromDistanceMatrix(
distances, knn, true, report_progress != 0);
// Compute geodesic distance by Floyd or Dijkstra's algorithm.
Mat geodesic(n,n);
real big_value = REAL_MAX / 3.0; // To make sure no overflow.
PP<ProgressBar> pb;
if (report_progress)
pb = new ProgressBar("Computing geodesic distances", n);
if (shortest_algo == "floyd") {
// First initialize the geodesic distances matrix.
geodesic.fill(big_value);
int neighbor;
real d;
for (int i = 0; i < n; i++) {
geodesic(i,i) = 0;
for (int j = 1; j < knn; j++) {
neighbor = neighborhoods(i,j);
d = distances(i, neighbor);
geodesic(i, neighbor) = d;
geodesic(neighbor, i) = d;
}
}
// And iterate to find geodesic distances.
real dist;
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dist = geodesic(i,k) + geodesic(k,j);
if (geodesic(i,j) > dist) {
geodesic(i,j) = dist;
}
}
}
if (report_progress)
pb->update(k + 1);
}
} else if (shortest_algo == "dijkstra") {
// First build a symmetric neighborhoods matrix
// (j is a neighbor of i if it was already a neighbor, or if i was a
// neighbor of j).
TVec< TVec<int> > sym_neighborhoods(n);
int neighb, i;
for (i = 0; i < n; i++) {
for (int j = 1; j < knn; j++) {
neighb = neighborhoods(i, j);
sym_neighborhoods[i].append(neighb);
sym_neighborhoods[neighb].append(i);
}
}
Vec d;
TVec<bool> T(n);
int t, min, j, m, k;
real dist;
for (k = 0; k < n; k++) {
d = geodesic(k);
d.fill(big_value);
d[k] = 0;
T.fill(true);
for (i = 0; i < n; i++) {
min = 0;
while (!T[min])
min++;
for (m = min + 1; m < n; m++) {
if (T[m] && d[m] < d[min]) {
min = m;
}
}
for (j = 0; j < sym_neighborhoods[min].length(); j++) {
t = sym_neighborhoods[min][j];
if (T[t]) {
dist = d[min] + distances(min, t);
if (d[t] > dist) {
d[t] = dist;
}
}
}
T[min] = false;
}
if (report_progress)
pb->update(k+1);
}
} else {
PLERROR("In GeodesicDistanceKernel::setDataForKernelMatrix - Unknown "
"value for 'shortest_algo': %s",
shortest_algo.c_str());
}
// Save the result in geo_distances.
if (geodesic_file.isEmpty()) {
geo_distances = VMat(geodesic);
} else {
// Use a FileVMatrix to save on disk.
geo_distances = new FileVMatrix(geodesic_file, n, n);
geo_distances->putMat(0, 0, geodesic);
}
}
Reimplemented from PLearn::Kernel.
Definition at line 124 of file GeodesicDistanceKernel.h.
Mat PLearn::GeodesicDistanceKernel::dist_xi_x_sorted [mutable, private] |
Definition at line 60 of file GeodesicDistanceKernel.h.
Referenced by evaluate_i_x_again(), and makeDeepCopyFromShallowCopy().
Mat PLearn::GeodesicDistanceKernel::dist_xi_x_sorted1 [mutable, private] |
Used to store data and save memory allocation.
Definition at line 60 of file GeodesicDistanceKernel.h.
Referenced by evaluate(), and makeDeepCopyFromShallowCopy().
Mat PLearn::GeodesicDistanceKernel::dist_xi_x_sorted2 [mutable, private] |
Definition at line 60 of file GeodesicDistanceKernel.h.
Referenced by evaluate(), and makeDeepCopyFromShallowCopy().
Definition at line 74 of file GeodesicDistanceKernel.h.
Referenced by declareOptions(), evaluate(), evaluate_i_x_again(), GeodesicDistanceKernel(), makeDeepCopyFromShallowCopy(), and setDataForKernelMatrix().
Definition at line 79 of file GeodesicDistanceKernel.h.
Referenced by computeNearestGeodesicNeighbour(), declareOptions(), evaluate(), evaluate_i_j(), makeDeepCopyFromShallowCopy(), and setDataForKernelMatrix().
Definition at line 75 of file GeodesicDistanceKernel.h.
Referenced by declareOptions(), and setDataForKernelMatrix().
Definition at line 76 of file GeodesicDistanceKernel.h.
Referenced by computeNearestGeodesicNeighbour(), declareOptions(), evaluate(), evaluate_i_x_again(), and setDataForKernelMatrix().
Definition at line 77 of file GeodesicDistanceKernel.h.
Referenced by declareOptions(), evaluate(), evaluate_i_j(), evaluate_i_x_again(), and evaluate_i_x_from_distances().
Definition at line 78 of file GeodesicDistanceKernel.h.
Referenced by declareOptions(), and setDataForKernelMatrix().
 1.7.4
1.7.4