|
PLearn 0.1
|
|
PLearn 0.1
|
This class implements the negative log-likelihood cost of a Markov chain that uses semispherical gaussian transition probabilities. More...
#include <NllSemisphericalGaussianVariable.h>
Public Member Functions | |
| NllSemisphericalGaussianVariable () | |
| Default constructor for persistence. | |
| NllSemisphericalGaussianVariable (const VarArray &the_varray, bool that_use_noise, real theepsilon, real min_p_x, int mu_n_neighbors) | |
| virtual string | classname () const |
| virtual OptionList & | getOptionList () const |
| virtual OptionMap & | getOptionMap () const |
| virtual RemoteMethodMap & | getRemoteMethodMap () const |
| virtual NllSemisphericalGaussianVariable * | deepCopy (CopiesMap &copies) const |
| virtual void | build () |
| Post-constructor. | |
| virtual void | recomputeSize (int &l, int &w) const |
| Recomputes the length l and width w that this variable should have, according to its parent variables. | |
| virtual void | fprop () |
| compute output given input | |
| virtual void | bprop () |
| virtual void | symbolicBprop () |
| compute a piece of new Var graph that represents the symbolic derivative of this Var | |
Static Public Member Functions | |
| static string | _classname_ () |
| NllSemisphericalGaussianVariable. | |
| static OptionList & | _getOptionList_ () |
| static RemoteMethodMap & | _getRemoteMethodMap_ () |
| static Object * | _new_instance_for_typemap_ () |
| static bool | _isa_ (const Object *o) |
| static void | _static_initialize_ () |
| static const PPath & | declaringFile () |
Public Attributes | |
| int | n |
| bool | use_subspace_distance |
| bool | use_noise |
| real | epsilon |
| real | min_p_x |
| int | n_dim |
| int | n_neighbors |
| int | mu_n_neighbors |
| Vec | mu |
| Vec | sm |
| Vec | sn |
| Vec | S |
| Vec | noise |
| Vec | mu_noisy |
| Mat | F |
| Mat | diff_y_x |
| Mat | z |
| Mat | B |
| Mat | Ut |
| Mat | V |
| Mat | zn |
| Mat | zm |
| Mat | z_noisy |
| Mat | zn_noisy |
| Mat | zm_noisy |
| Vec | p_neighbors |
| Vec | p_target |
| Mat | w |
Static Public Attributes | |
| static StaticInitializer | _static_initializer_ |
Protected Member Functions | |
| void | build_ () |
| Object-specific post-constructor. | |
Private Types | |
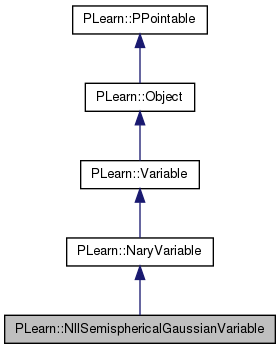
| typedef NaryVariable | inherited |
This class implements the negative log-likelihood cost of a Markov chain that uses semispherical gaussian transition probabilities.
The parameters of the semispherical gaussians are a tangent plane, two variances, one mean and the distance of the point with its nearest neighbors. The two variances correspond to the shared variance of every manifold directions and of every noise directions. This variable is used to do gradient descent on the parameters, but not to estimate de likelihood of the Markov chain a some point, which is more complex to estimate.
Definition at line 56 of file NllSemisphericalGaussianVariable.h.
typedef NaryVariable PLearn::NllSemisphericalGaussianVariable::inherited [private] |
Reimplemented from PLearn::NaryVariable.
Definition at line 58 of file NllSemisphericalGaussianVariable.h.
| PLearn::NllSemisphericalGaussianVariable::NllSemisphericalGaussianVariable | ( | ) | [inline] |
Default constructor for persistence.
Definition at line 75 of file NllSemisphericalGaussianVariable.h.
{}
| PLearn::NllSemisphericalGaussianVariable::NllSemisphericalGaussianVariable | ( | const VarArray & | the_varray, |
| bool | that_use_noise, | ||
| real | theepsilon, | ||
| real | min_p_x, | ||
| int | mu_n_neighbors | ||
| ) |
Definition at line 66 of file NllSemisphericalGaussianVariable.cc.
References build_().
: inherited(the_varray,the_varray[4]->length(),1), n(varray[0]->width()), use_noise(that_use_noise),epsilon(theepsilon), min_p_x(themin_p_x), n_dim(varray[0]->length()), n_neighbors(varray[4]->length()), mu_n_neighbors(the_mu_n_neighbors) { build_(); }

| string PLearn::NllSemisphericalGaussianVariable::_classname_ | ( | ) | [static] |
NllSemisphericalGaussianVariable.
Reimplemented from PLearn::NaryVariable.
Definition at line 64 of file NllSemisphericalGaussianVariable.cc.
| OptionList & PLearn::NllSemisphericalGaussianVariable::_getOptionList_ | ( | ) | [static] |
Reimplemented from PLearn::NaryVariable.
Definition at line 64 of file NllSemisphericalGaussianVariable.cc.
| RemoteMethodMap & PLearn::NllSemisphericalGaussianVariable::_getRemoteMethodMap_ | ( | ) | [static] |
Reimplemented from PLearn::NaryVariable.
Definition at line 64 of file NllSemisphericalGaussianVariable.cc.
Reimplemented from PLearn::NaryVariable.
Definition at line 64 of file NllSemisphericalGaussianVariable.cc.
| Object * PLearn::NllSemisphericalGaussianVariable::_new_instance_for_typemap_ | ( | ) | [static] |
Reimplemented from PLearn::Object.
Definition at line 64 of file NllSemisphericalGaussianVariable.cc.
| StaticInitializer NllSemisphericalGaussianVariable::_static_initializer_ & PLearn::NllSemisphericalGaussianVariable::_static_initialize_ | ( | ) | [static] |
Reimplemented from PLearn::NaryVariable.
Definition at line 64 of file NllSemisphericalGaussianVariable.cc.
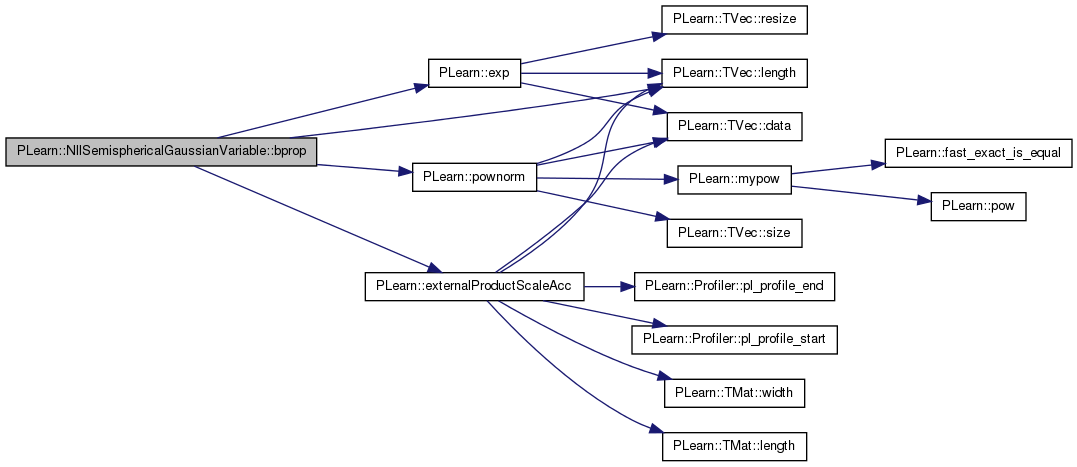
| void PLearn::NllSemisphericalGaussianVariable::bprop | ( | ) | [virtual] |
Implements PLearn::Variable.
Definition at line 237 of file NllSemisphericalGaussianVariable.cc.
References PLearn::exp(), PLearn::externalProductScaleAcc(), PLearn::Variable::gradient, i, PLearn::TVec< T >::length(), PLearn::Variable::matGradient, mu, mu_n_neighbors, mu_noisy, n, n_dim, n_neighbors, p_neighbors, p_target, PLearn::pownorm(), sm, sn, use_noise, PLearn::Variable::value, PLearn::NaryVariable::varray, w, zm, zm_noisy, zn, and zn_noisy.
{
if(n_neighbors < mu_n_neighbors) mu_n_neighbors = n_neighbors;
for(int neighbor=0; neighbor<n_neighbors; neighbor++)
{
// dNLL/dF
/*
for(int i=0; i<F.length(); i++)
for(int j=0; j<F.width(); j++)
//varray[0]->matGradient(i,j) += gradient[neighbor]*exp(-1.0*value[neighbor] + p_target[0] - p_neighbors[neighbor]) * (1/sm[0] - 1/sn[0]) * w(neighbor,i) * zn(neighbor,j);
varray[0]->matGradient(i,j) += gradient[neighbor]*exp(p_target[0]) * (1/sm[0] - 1/sn[0]) * w(neighbor,i) * zn(neighbor,j);
*/
externalProductScaleAcc(varray[0]->matGradient,w(neighbor),zn(neighbor),gradient[neighbor]*exp(p_target[0]) * (1/sm[0] - 1/sn[0]));
if(neighbor < mu_n_neighbors)
{
// dNLL/dmu
if(!use_noise)
{
for(int i=0; i<mu.length(); i++)
//varray[1]->gradient[i] -= ((real)n_neighbors)/(mu_n_neighbors)*gradient[neighbor]*exp(-1.0*value[neighbor] + p_target[0] - p_neighbors[neighbor])*( 1/sm[0] * zm(neighbor,i) + 1/sn[0] * zn(neighbor,i));
varray[1]->gradient[i] -= ((real)n_neighbors)/(mu_n_neighbors)*gradient[neighbor]*exp(p_target[0])*( 1/sm[0] * zm(neighbor,i) + 1/sn[0] * zn(neighbor,i));
}
else
{
// dNLL/dmu with noisy data
for(int i=0; i<mu_noisy.length(); i++)
varray[8]->gradient[i] -= ((real)n_neighbors)/(mu_n_neighbors)*gradient[neighbor]*exp(-1.0*value[neighbor] + p_target[0] - p_neighbors[neighbor])* ( 1/sm[0] * zm_noisy(neighbor,i) + 1/sn[0] * zn_noisy(neighbor,i));
}
}
// dNLL/dsm
//varray[2]->gradient[0] += gradient[neighbor]*exp(-1.0*value[neighbor] + p_target[0] - p_neighbors[neighbor])* (0.5 * n_dim/sm[0] - pownorm(zm(neighbor),2)/(sm[0]*sm[0]))/(n_dim*n_dim);
varray[2]->gradient[0] += gradient[neighbor]*exp(p_target[0])* (0.5 * n_dim/sm[0] - pownorm(zm(neighbor),2)/(sm[0]*sm[0]));
// dNLL/dsn
// varray[3]->gradient[0] += gradient[neighbor]*exp(-1.0*value[neighbor] + p_target[0] - p_neighbors[neighbor])* (0.5 * (n-n_dim)/sn[0] - pownorm(zn(neighbor),2)/(sn[0]*sn[0]))/(n*n);
varray[3]->gradient[0] += gradient[neighbor]*exp(p_target[0])* (0.5 * (n-n_dim)/sn[0] - pownorm(zn(neighbor),2)/(sn[0]*sn[0]));
}
//cout << "value = " << value << " p_neighbors = " << p_neighbors << endl;
}
| void PLearn::NllSemisphericalGaussianVariable::build | ( | ) | [virtual] |
Post-constructor.
The normal implementation should call simply inherited::build(), then this class's build_(). This method should be callable again at later times, after modifying some option fields to change the "architecture" of the object.
Reimplemented from PLearn::NaryVariable.
Definition at line 75 of file NllSemisphericalGaussianVariable.cc.
References PLearn::NaryVariable::build(), and build_().
{
inherited::build();
build_();
}
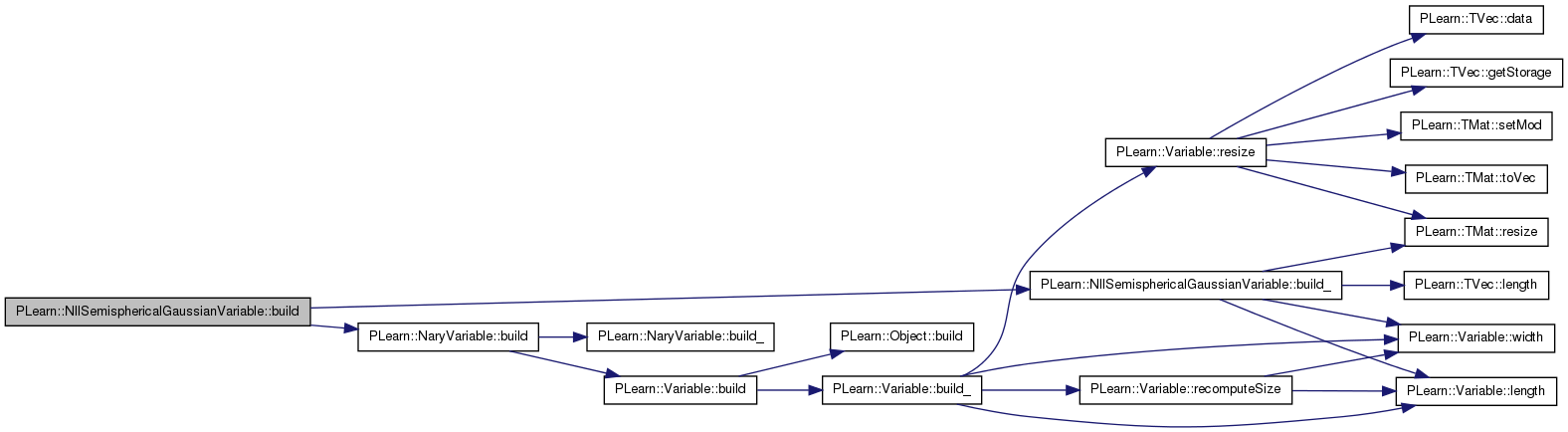
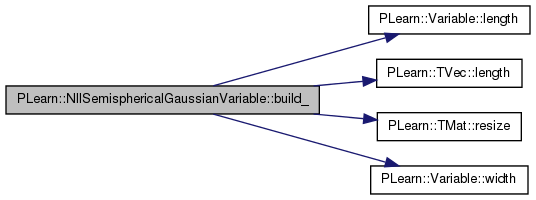
| void PLearn::NllSemisphericalGaussianVariable::build_ | ( | ) | [protected] |
Object-specific post-constructor.
This method should be redefined in subclasses and do the actual building of the object according to previously set option fields. Constructors can just set option fields, and then call build_. This method is NOT virtual, and will typically be called only from three places: a constructor, the public virtual build() method, and possibly the public virtual read method (which calls its parent's read). build_() can assume that its parent's build_() has already been called.
Reimplemented from PLearn::NaryVariable.
Definition at line 82 of file NllSemisphericalGaussianVariable.cc.
References B, diff_y_x, F, PLearn::Variable::length(), PLearn::TVec< T >::length(), mu, mu_n_neighbors, mu_noisy, n, n_dim, n_neighbors, noise, p_neighbors, p_target, PLERROR, PLearn::TMat< T >::resize(), sm, sn, Ut, V, PLearn::NaryVariable::varray, w, PLearn::Variable::width(), z, z_noisy, zm, zm_noisy, zn, and zn_noisy.
Referenced by build(), and NllSemisphericalGaussianVariable().
{
// The VarArray constaints the following variables:
// - varray[0] = the tangent plane (n_dim x n)
// - varray[1] = mu(data_point) (n x 1)
// - varray[2] = sigma_manifold (1 x 1)
// - varray[3] = sigma_noise (1 x 1)
// - varray[4] = neighbor_distances (n_neighbors x n)
// - varray[5] = p_target (1 x 1)
// - varray[6] = p_neighbors (n_neighbors x 1)
// - varray[7] = noisy x (n x 1)
if(varray.length() != 9)
PLERROR("In NllSemisphericalGaussianVariable constructor: varray is of length %d but should be of length %d", varray.length(), 7);
if(varray[1]->length() != n || varray[1]->width() != 1) PLERROR("In NllSemisphericalGaussianVariable constructor: varray[1] is of size (%d,%d), but should be of size (%d,%d)",
varray[1]->length(), varray[1]->width(),
n_dim, 1);
if(varray[2]->length() != 1 || varray[2]->width() != 1) PLERROR("In NllSemisphericalGaussianVariable constructor: varray[2] is of size (%d,%d), but should be of size (%d,%d)",
varray[2]->length(), varray[2]->width(),
1, 1);
if(varray[3]->length() != 1 || varray[3]->width() != 1) PLERROR("In NllSemisphericalGaussianVariable constructor: varray[3] is of size (%d,%d), but should be of size (%d,%d)",
varray[3]->length(), varray[3]->width(),
1, 1);
if(varray[4]->width() != n) PLERROR("In NllSemisphericalGaussianVariable constructor: varray[4] is of size (%d,%d), but should be of size (%d,%d)",
varray[4]->length(), varray[4]->width(),
n_neighbors, n);
if(varray[5]->length() != 1 || varray[5]->width() != 1) PLERROR("In NllSemisphericalGaussianVariable constructor: varray[5] is of size (%d,%d), but should be of size (%d,%d)",
varray[5]->length(), varray[5]->width(),
1, 1);
if(varray[6]->length() != n_neighbors || varray[6]->width() != 1) PLERROR("In NllSemisphericalGaussianVariable constructor: varray[6] is of size (%d,%d), but should be of size (%d,%d)",
varray[6]->length(), varray[6]->width(), n_neighbors, 1);
if(varray[7]->length() != n || varray[7]->width() != 1) PLERROR("In NllSemisphericalGaussianVariable constructor: varray[7] is of size (%d,%d), but should be of size (%d,%d)",
varray[7]->length(), varray[7]->width(), n, 1);
if(varray[8]->length() != n || varray[8]->width() != 1) PLERROR("In NllSemisphericalGaussianVariable constructor: varray[8] is of size (%d,%d), but should be of size (%d,%d)",
varray[8]->length(), varray[8]->width(), n, 1);
if(mu_n_neighbors < 0)
mu_n_neighbors = n_neighbors;
F = varray[0]->matValue;
mu = varray[1]->value;
sm = varray[2]->value;
sn = varray[3]->value;
diff_y_x = varray[4]->matValue;
z.resize(n_neighbors,n);
zm.resize(n_neighbors,n);
zn.resize(n_neighbors,n);
z_noisy.resize(n_neighbors,n);
zm_noisy.resize(n_neighbors,n);
zn_noisy.resize(n_neighbors,n);
B.resize(n_dim,n);
Ut.resize(n,n);
V.resize(n_dim,n_dim);
w.resize(n_neighbors,n_dim);
p_target = varray[5]->value;
p_neighbors = varray[6]->value;
noise = varray[7]->value;
mu_noisy = varray[8]->value;
}

| string PLearn::NllSemisphericalGaussianVariable::classname | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 64 of file NllSemisphericalGaussianVariable.cc.
| static const PPath& PLearn::NllSemisphericalGaussianVariable::declaringFile | ( | ) | [inline, static] |
Reimplemented from PLearn::NaryVariable.
Definition at line 78 of file NllSemisphericalGaussianVariable.h.
:
void build_();
| NllSemisphericalGaussianVariable * PLearn::NllSemisphericalGaussianVariable::deepCopy | ( | CopiesMap & | copies | ) | const [virtual] |
Reimplemented from PLearn::NaryVariable.
Definition at line 64 of file NllSemisphericalGaussianVariable.cc.
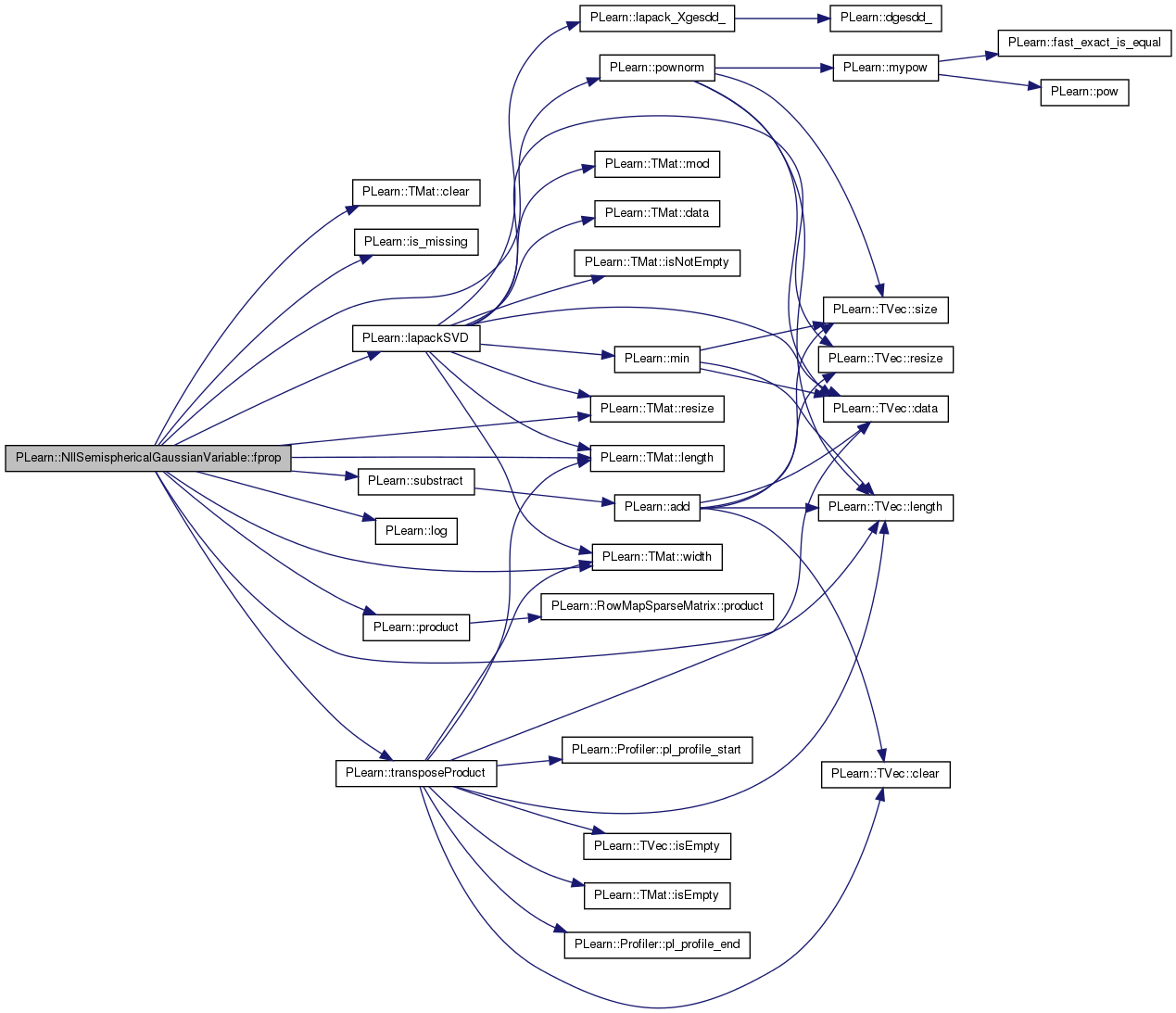
| void PLearn::NllSemisphericalGaussianVariable::fprop | ( | ) | [virtual] |
compute output given input
Implements PLearn::Variable.
Definition at line 153 of file NllSemisphericalGaussianVariable.cc.
References B, PLearn::TMat< T >::clear(), diff_y_x, epsilon, F, i, PLearn::is_missing(), j, PLearn::lapackSVD(), PLearn::TVec< T >::length(), PLearn::TMat< T >::length(), PLearn::log(), Log2Pi, mu, mu_noisy, n, n_dim, n_neighbors, noise, p_neighbors, PLearn::pownorm(), PLearn::product(), PLearn::TMat< T >::resize(), S, sm, sn, PLearn::substract(), PLearn::transposeProduct(), Ut, V, PLearn::Variable::value, w, PLearn::TMat< T >::width(), z, z_noisy, zm, zm_noisy, zn, and zn_noisy.
{
// Let F the tangent plan matrix with rows f_i.
// We need to solve the system
// F F' w_j = F z_j
// where z_j is the distance between the data point and the j_th neighbor,
// to find the solution w_j of
// min_{w_j} || z_j - sum_i w_{ji} f_i ||^2
// for each j. Then sum over j the above square errors.
// Let F' = U D V' the SVD of F'. Then
// w_j = (F F')^{-1} F t_j = (V D U' U D V')^{-1} F t_j = V D^{-2} V' V D U' z_j
// = V D^{-1} U' z_j
// = B z_j
//
// Compute w
static Mat F_copy;
F_copy.resize(F.length(),F.width());
F_copy << F;
// N.B. this is the SVD of F'
lapackSVD(F_copy, Ut, S, V,'A',1.5);
B.clear();
for (int k=0;k<S.length();k++)
{
real s_k = S[k];
if (s_k>epsilon) // ignore the components that have too small singular value (more robust solution)
{
real coef = 1/s_k;
for (int i=0;i<n_dim;i++)
{
real* Bi = B[i];
for (int j=0;j<n;j++)
Bi[j] += V(i,k)*Ut(k,j)*coef;
}
}
}
// now that we have B, we can compute the w's and the nll for every neighbors
/*
Vec mean_diff(n); mean_diff.clear();
for(int j=0; j<n_neighbors;j++)
{
mean_diff += diff_y_x(j);
}
mean_diff /= n_neighbors;
*/
for(int j=0; j<n_neighbors;j++)
{
Vec zj = z(j);
//substract(diff_y_x(j),mean_diff,zj); // z = y - x - mean_diff
substract(diff_y_x(j),mu,zj); // z = y - x - mu(x)
Vec zmj = zm(j);
Vec znj = zn(j);
Vec wj = w(j);
product(wj, B, zj); // w = B * z = projection weights for neighbor j
transposeProduct(zmj, F, wj); // F' w = z_m
substract(zj,zmj,znj); // z_n = z - zm
value[j] = 0.5*(pownorm(zmj,2)/sm[0] + pownorm(znj,2)/sn[0] + n_dim*log(sm[0]) + (n-n_dim)*log(sn[0])) + n/2.0 * Log2Pi; // This value is not really -log(p(y))
if(is_missing(p_neighbors[j]))
p_neighbors[j] = -1.0*value[j];
}
// and we can make the noisy zm and zn
for(int j=0; j<n_neighbors;j++)
{
Vec zj_noisy = z_noisy(j);
Vec diff_noisy(n);
substract(diff_y_x(j),noise,diff_noisy);
substract(diff_noisy,mu_noisy,zj_noisy); // z = y - x - mu(x)
Vec zmj_noisy = zm_noisy(j);
Vec znj_noisy = zn_noisy(j);
Vec wj_noisy(n_dim);
product(wj_noisy, B, zj_noisy); // w = B * z = projection weights for neighbor j
transposeProduct(zmj_noisy, F, wj_noisy); // F' w = z_m
substract(zj_noisy,zmj_noisy,znj_noisy); // z_n = z - zm
}
}
| OptionList & PLearn::NllSemisphericalGaussianVariable::getOptionList | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 64 of file NllSemisphericalGaussianVariable.cc.
| OptionMap & PLearn::NllSemisphericalGaussianVariable::getOptionMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 64 of file NllSemisphericalGaussianVariable.cc.
| RemoteMethodMap & PLearn::NllSemisphericalGaussianVariable::getRemoteMethodMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 64 of file NllSemisphericalGaussianVariable.cc.
Recomputes the length l and width w that this variable should have, according to its parent variables.
This is used for ex. by sizeprop() The default version stupidly returns the current dimensions, so make sure to overload it in subclasses if this is not appropriate.
Reimplemented from PLearn::Variable.
Definition at line 147 of file NllSemisphericalGaussianVariable.cc.
References PLearn::TVec< T >::length(), and PLearn::NaryVariable::varray.
{
len = varray[4]->length();
wid = 1;
}

| void PLearn::NllSemisphericalGaussianVariable::symbolicBprop | ( | ) | [virtual] |
compute a piece of new Var graph that represents the symbolic derivative of this Var
Reimplemented from PLearn::Variable.
Definition at line 288 of file NllSemisphericalGaussianVariable.cc.
References PLERROR.
{
PLERROR("Not implemented");
}
Reimplemented from PLearn::NaryVariable.
Definition at line 78 of file NllSemisphericalGaussianVariable.h.
Definition at line 70 of file NllSemisphericalGaussianVariable.h.
Definition at line 70 of file NllSemisphericalGaussianVariable.h.
Definition at line 64 of file NllSemisphericalGaussianVariable.h.
Referenced by fprop().
Definition at line 70 of file NllSemisphericalGaussianVariable.h.
Definition at line 65 of file NllSemisphericalGaussianVariable.h.
Definition at line 69 of file NllSemisphericalGaussianVariable.h.
Definition at line 68 of file NllSemisphericalGaussianVariable.h.
Definition at line 69 of file NllSemisphericalGaussianVariable.h.
Definition at line 61 of file NllSemisphericalGaussianVariable.h.
Definition at line 66 of file NllSemisphericalGaussianVariable.h.
Definition at line 67 of file NllSemisphericalGaussianVariable.h.
Definition at line 69 of file NllSemisphericalGaussianVariable.h.
Definition at line 71 of file NllSemisphericalGaussianVariable.h.
Definition at line 71 of file NllSemisphericalGaussianVariable.h.
Definition at line 69 of file NllSemisphericalGaussianVariable.h.
Referenced by fprop().
Definition at line 69 of file NllSemisphericalGaussianVariable.h.
Definition at line 69 of file NllSemisphericalGaussianVariable.h.
Definition at line 63 of file NllSemisphericalGaussianVariable.h.
Referenced by bprop().
Definition at line 62 of file NllSemisphericalGaussianVariable.h.
Definition at line 70 of file NllSemisphericalGaussianVariable.h.
Definition at line 70 of file NllSemisphericalGaussianVariable.h.
Definition at line 72 of file NllSemisphericalGaussianVariable.h.
Definition at line 70 of file NllSemisphericalGaussianVariable.h.
Definition at line 70 of file NllSemisphericalGaussianVariable.h.
Definition at line 70 of file NllSemisphericalGaussianVariable.h.
Definition at line 70 of file NllSemisphericalGaussianVariable.h.
Definition at line 70 of file NllSemisphericalGaussianVariable.h.
Definition at line 70 of file NllSemisphericalGaussianVariable.h.
 1.7.4
1.7.4