|
PLearn 0.1
|
|
PLearn 0.1
|
#include <NllGeneralGaussianVariable.h>
Public Member Functions | |
| NllGeneralGaussianVariable () | |
| Default constructor for persistence. | |
| NllGeneralGaussianVariable (const VarArray &the_varray, real thelogL, bool use_mu, int mu_nneighbors) | |
| virtual string | classname () const |
| virtual OptionList & | getOptionList () const |
| virtual OptionMap & | getOptionMap () const |
| virtual RemoteMethodMap & | getRemoteMethodMap () const |
| virtual NllGeneralGaussianVariable * | deepCopy (CopiesMap &copies) const |
| virtual void | build () |
| Post-constructor. | |
| virtual void | recomputeSize (int &l, int &w) const |
| Recomputes the length l and width w that this variable should have, according to its parent variables. | |
| virtual void | fprop () |
| compute output given input | |
| virtual void | bprop () |
| virtual void | symbolicBprop () |
| compute a piece of new Var graph that represents the symbolic derivative of this Var | |
| virtual void | makeDeepCopyFromShallowCopy (CopiesMap &copies) |
| Does the necessary operations to transform a shallow copy (this) into a deep copy by deep-copying all the members that need to be. | |
Static Public Member Functions | |
| static string | _classname_ () |
| NllGeneralGaussianVariable. | |
| static OptionList & | _getOptionList_ () |
| static RemoteMethodMap & | _getRemoteMethodMap_ () |
| static Object * | _new_instance_for_typemap_ () |
| static bool | _isa_ (const Object *o) |
| static void | _static_initialize_ () |
| static const PPath & | declaringFile () |
Public Attributes | |
| real | log_L |
| Log of number of components L. | |
| bool | use_mu |
| Indication that a parameter corresponding to the difference between the Gaussian center and the input data point position should be used. | |
| int | mu_nneighbors |
| Number of nearest neighbors to learn mu, which must be < then nneighbors. | |
Static Public Attributes | |
| static StaticInitializer | _static_initializer_ |
Protected Member Functions | |
| void | build_ () |
| Object-specific post-constructor. | |
Protected Attributes | |
| int | n |
| Dimensionality of the input vectors. | |
| int | ncomponents |
| Number of components (i.e. number of vectors in f) | |
| int | nneighbors |
| Number of nearest neighbors. | |
| real | tr_inv_Sigma |
| Trace of the inverse of the covariance matrix. | |
| Vec | input |
| Temporary storage variables. | |
| Vec | diff_neighbor_input |
| Vec | mu |
| Vec | sm_svd |
| Vec | sn |
| Vec | S |
| Vec | uk |
| Vec | fk |
| Vec | uk2 |
| Vec | inv_sigma_zj |
| Vec | zj |
| Vec | inv_sigma_fk |
| Vec | temp_ncomp |
| Mat | neighbors |
| Mat | F |
| Mat | F_copy |
| Mat | z |
| Mat | U |
| Mat | Ut |
| Mat | V |
| Mat | inv_Sigma_F |
| Mat | inv_Sigma_z |
Private Types | |
| typedef NaryVariable | inherited |
Private Member Functions | |
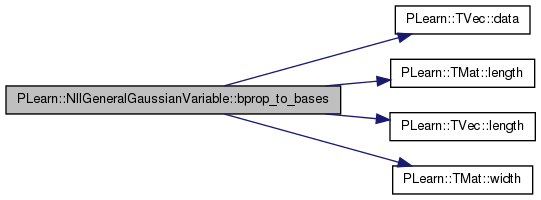
| void | bprop_to_bases (const Mat &R, const Mat &M, const Vec &v1, const Vec &v2, real alpha) |
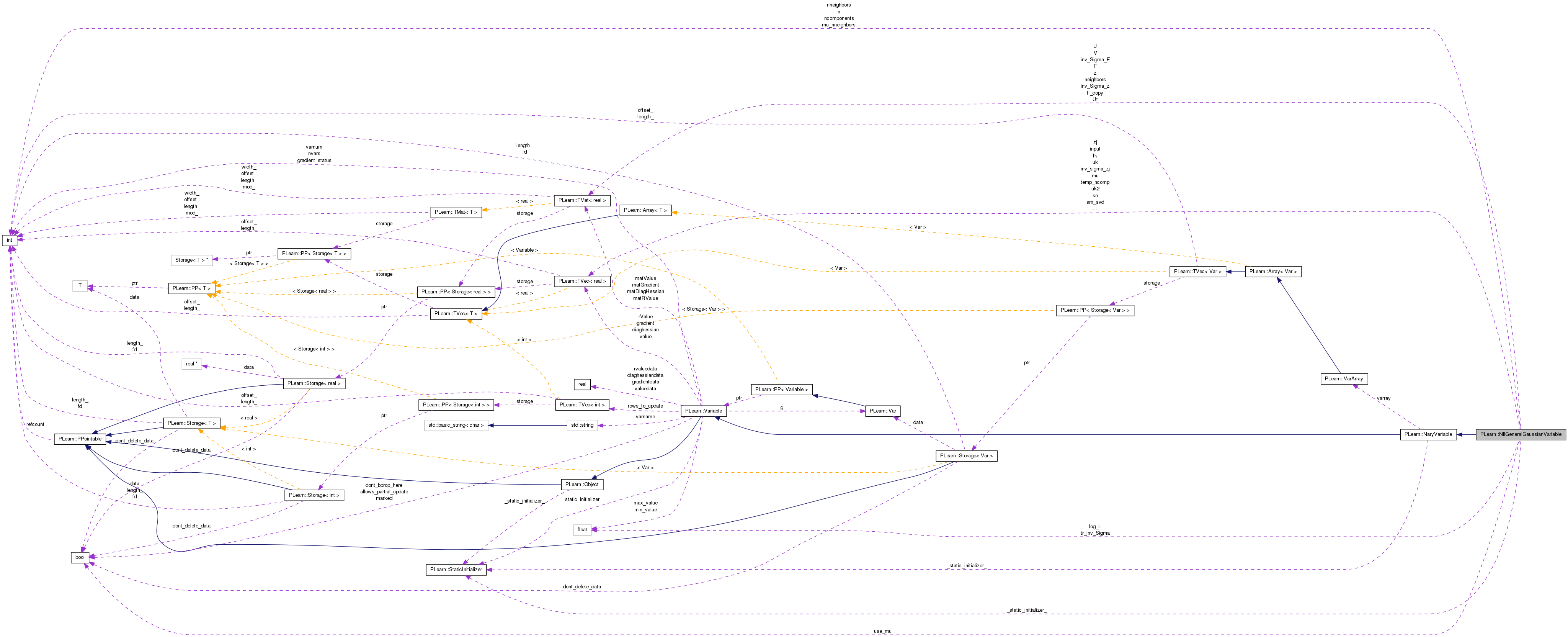
Definition at line 46 of file NllGeneralGaussianVariable.h.
typedef NaryVariable PLearn::NllGeneralGaussianVariable::inherited [private] |
Reimplemented from PLearn::NaryVariable.
Definition at line 48 of file NllGeneralGaussianVariable.h.
| PLearn::NllGeneralGaussianVariable::NllGeneralGaussianVariable | ( | ) | [inline] |
| PLearn::NllGeneralGaussianVariable::NllGeneralGaussianVariable | ( | const VarArray & | the_varray, |
| real | thelogL, | ||
| bool | use_mu, | ||
| int | mu_nneighbors | ||
| ) |
Definition at line 73 of file NllGeneralGaussianVariable.cc.
References build_().
: inherited(the_varray,the_varray[3]->length(),1), n(varray[3]->size()), ncomponents(varray[0]->length()%varray[3]->size()), nneighbors(varray[4]->length()), log_L(thelogL), use_mu(the_use_mu), mu_nneighbors(the_mu_nneighbors) { build_(); }
| string PLearn::NllGeneralGaussianVariable::_classname_ | ( | ) | [static] |
Reimplemented from PLearn::NaryVariable.
Definition at line 71 of file NllGeneralGaussianVariable.cc.
| OptionList & PLearn::NllGeneralGaussianVariable::_getOptionList_ | ( | ) | [static] |
Reimplemented from PLearn::NaryVariable.
Definition at line 71 of file NllGeneralGaussianVariable.cc.
| RemoteMethodMap & PLearn::NllGeneralGaussianVariable::_getRemoteMethodMap_ | ( | ) | [static] |
Reimplemented from PLearn::NaryVariable.
Definition at line 71 of file NllGeneralGaussianVariable.cc.
Reimplemented from PLearn::NaryVariable.
Definition at line 71 of file NllGeneralGaussianVariable.cc.
| Object * PLearn::NllGeneralGaussianVariable::_new_instance_for_typemap_ | ( | ) | [static] |
Reimplemented from PLearn::Object.
Definition at line 71 of file NllGeneralGaussianVariable.cc.
| StaticInitializer NllGeneralGaussianVariable::_static_initializer_ & PLearn::NllGeneralGaussianVariable::_static_initialize_ | ( | ) | [static] |
Reimplemented from PLearn::NaryVariable.
Definition at line 71 of file NllGeneralGaussianVariable.cc.
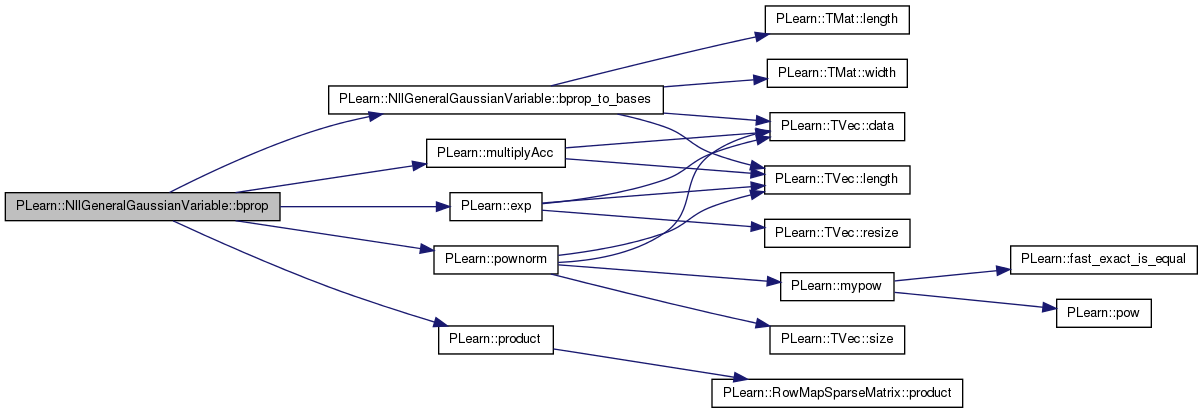
| void PLearn::NllGeneralGaussianVariable::bprop | ( | ) | [virtual] |
Implements PLearn::Variable.
Definition at line 257 of file NllGeneralGaussianVariable.cc.
References bprop_to_bases(), PLearn::exp(), F, PLearn::Variable::gradient, inv_Sigma_F, inv_Sigma_z, log_L, PLearn::Variable::matGradient, mu_nneighbors, PLearn::multiplyAcc(), nneighbors, PLearn::pownorm(), PLearn::product(), temp_ncomp, tr_inv_Sigma, use_mu, and PLearn::NaryVariable::varray.
{
real coef = exp(-log_L);
for(int neighbor=0; neighbor<nneighbors; neighbor++)
{
// dNLL/dF
product(temp_ncomp,F,inv_Sigma_z(neighbor));
bprop_to_bases(varray[0]->matGradient,inv_Sigma_F,
temp_ncomp,inv_Sigma_z(neighbor),
gradient[neighbor]*coef);
if(use_mu && neighbor < mu_nneighbors)
{
// dNLL/dmu
multiplyAcc(varray[1]->gradient, inv_Sigma_z(neighbor),
-1.0*gradient[neighbor] *coef) ;
}
// dNLL/dsn
varray[2]->gradient[0] += gradient[neighbor]*coef*
0.5*(tr_inv_Sigma - pownorm(inv_Sigma_z(neighbor)));
}
}
| void PLearn::NllGeneralGaussianVariable::bprop_to_bases | ( | const Mat & | R, |
| const Mat & | M, | ||
| const Vec & | v1, | ||
| const Vec & | v2, | ||
| real | alpha | ||
| ) | [private] |
Definition at line 234 of file NllGeneralGaussianVariable.cc.
References PLearn::TVec< T >::data(), i, j, PLearn::TMat< T >::length(), PLearn::TVec< T >::length(), PLERROR, and PLearn::TMat< T >::width().
Referenced by bprop().
{
#ifdef BOUNDCHECK
if (M.length() != R.length() || M.width() != R.width()
|| v1.length()!=M.length() || M.width()!=v2.length() )
PLERROR("NllGeneralGaussianVariable::bprop_to_bases(): incompatible "
"arguments' sizes");
#endif
const real* v_1=v1.data();
const real* v_2=v2.data();
for (int i=0;i<M.length();i++)
{
real* mi = M[i];
real* ri = R[i];
real v1i = v_1[i];
for (int j=0;j<M.width();j++)
ri[j] += alpha*(mi[j] - v1i * v_2[j]);
}
}

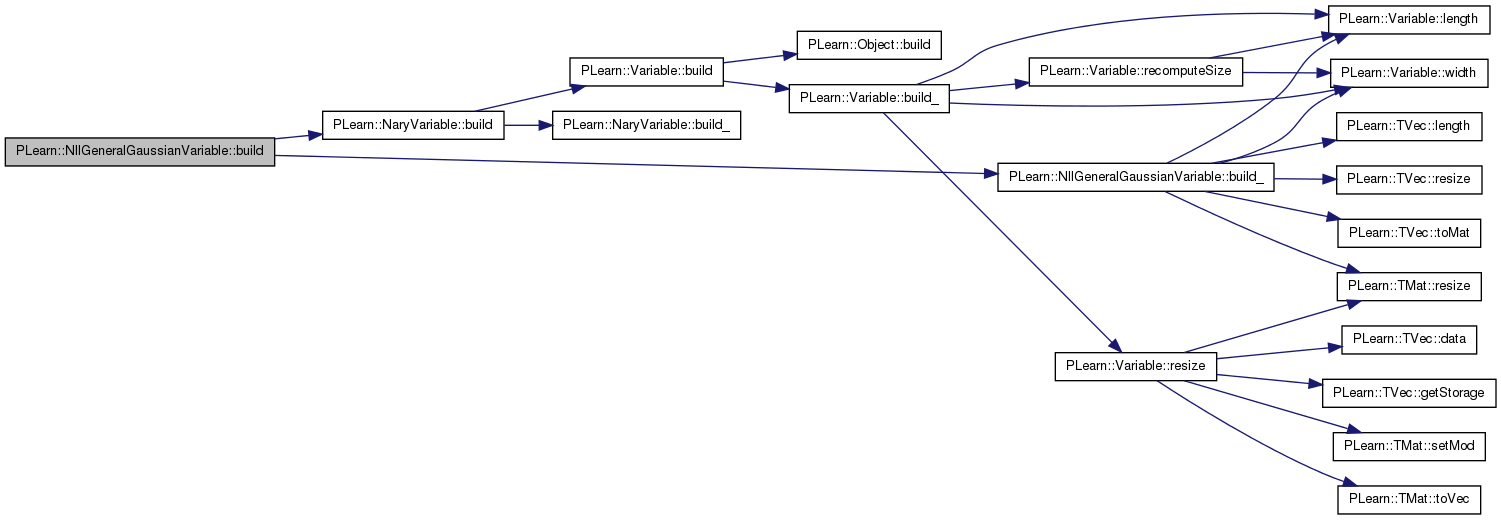
| void PLearn::NllGeneralGaussianVariable::build | ( | ) | [virtual] |
Post-constructor.
The normal implementation should call simply inherited::build(), then this class's build_(). This method should be callable again at later times, after modifying some option fields to change the "architecture" of the object.
Reimplemented from PLearn::NaryVariable.
Definition at line 87 of file NllGeneralGaussianVariable.cc.
References PLearn::NaryVariable::build(), and build_().
{
inherited::build();
build_();
}
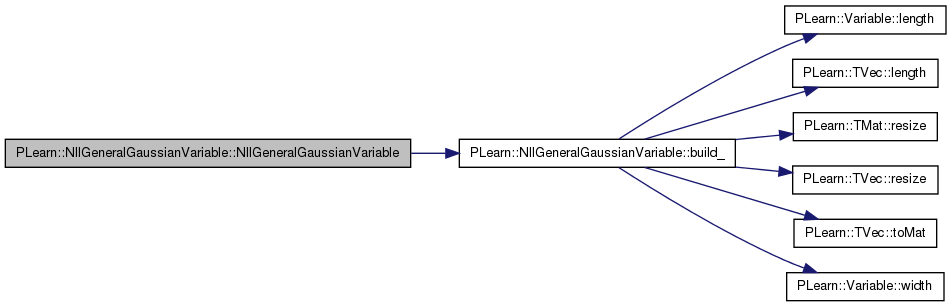
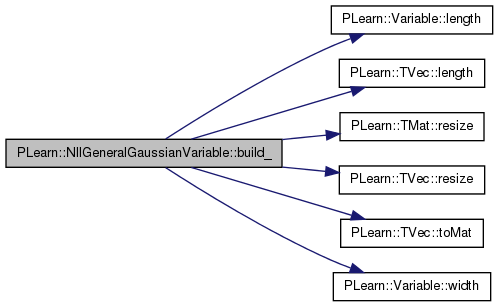
| void PLearn::NllGeneralGaussianVariable::build_ | ( | ) | [protected] |
Object-specific post-constructor.
This method should be redefined in subclasses and do the actual building of the object according to previously set option fields. Constructors can just set option fields, and then call build_. This method is NOT virtual, and will typically be called only from three places: a constructor, the public virtual build() method, and possibly the public virtual read method (which calls its parent's read). build_() can assume that its parent's build_() has already been called.
Reimplemented from PLearn::NaryVariable.
Definition at line 94 of file NllGeneralGaussianVariable.cc.
References diff_neighbor_input, F, input, inv_Sigma_F, inv_Sigma_z, PLearn::Variable::length(), PLearn::TVec< T >::length(), mu, mu_nneighbors, n, ncomponents, neighbors, nneighbors, PLERROR, PLearn::TMat< T >::resize(), PLearn::TVec< T >::resize(), sn, temp_ncomp, PLearn::TVec< T >::toMat(), U, use_mu, Ut, V, PLearn::NaryVariable::varray, PLearn::Variable::width(), and z.
Referenced by build(), and NllGeneralGaussianVariable().
{
// The VarArray constaints the following variables:
// - varray[0] = the tangent plane (ncomponents x n sized vector)
// - varray[1] = mu(data_point) (n x 1)
// - varray[2] = sigma_noise (1 x 1)
// - varray[3] = input data point around which the Gaussian is centered
// - varray[4] = nearest neighbors (nneighbors x n)
if(varray.length() != 5)
PLERROR("In NllGeneralGaussianVariable::build_(): varray is of "
"length %d but should be of length %d", varray.length(), 5);
if(varray[1]->length() != n || varray[1]->width() != 1)
PLERROR("In NllGeneralGaussianVariable::build_(): varray[1] "
"is of size (%d,%d), but should be of size (%d,%d)",
varray[1]->length(), varray[1]->width(),
ncomponents, 1);
if(varray[2]->length() != 1 || varray[2]->width() != 1)
PLERROR("In NllGeneralGaussianVariable::build_(): varray[2] "
"is of size (%d,%d), but should be of size (%d,%d)",
varray[2]->length(), varray[2]->width(),
1, 1);
if(varray[3]->length() != n || varray[3]->width() != 1)
PLERROR("In NllGeneralGaussianVariable::build_(): varray[3] "
"is of size (%d,%d), but should be of size (%d,%d)",
varray[3]->length(), varray[3]->width(),
n,1);
if(varray[4]->width() != n)
PLERROR("In NllGeneralGaussianVariable::build_(): varray[4] "
"is of size (%d,%d), but should be of size (%d,%d)",
varray[3]->length(), varray[3]->width(),
nneighbors, n);
if(mu_nneighbors < 0) mu_nneighbors = nneighbors;
if(mu_nneighbors > nneighbors)
PLERROR("In NllGeneralGaussianVariable::build_(): mu_nneighbors "
"cannot be > than number of provided neighbors");
F = varray[0]->value.toMat(ncomponents,n);
if(use_mu) mu = varray[1]->value;
sn = varray[2]->value;
input = varray[3]->value;
neighbors = varray[4]->matValue;
diff_neighbor_input.resize(n);
z.resize(nneighbors,n);
U.resize(ncomponents,n);
Ut.resize(n,n);
V.resize(ncomponents,ncomponents);
inv_Sigma_F.resize(ncomponents,n);
inv_Sigma_z.resize(nneighbors,n);
temp_ncomp.resize(ncomponents);
}

| string PLearn::NllGeneralGaussianVariable::classname | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 71 of file NllGeneralGaussianVariable.cc.
| static const PPath& PLearn::NllGeneralGaussianVariable::declaringFile | ( | ) | [inline, static] |
Reimplemented from PLearn::NaryVariable.
Definition at line 83 of file NllGeneralGaussianVariable.h.
:
void build_();
| NllGeneralGaussianVariable * PLearn::NllGeneralGaussianVariable::deepCopy | ( | CopiesMap & | copies | ) | const [virtual] |
Reimplemented from PLearn::NaryVariable.
Definition at line 71 of file NllGeneralGaussianVariable.cc.
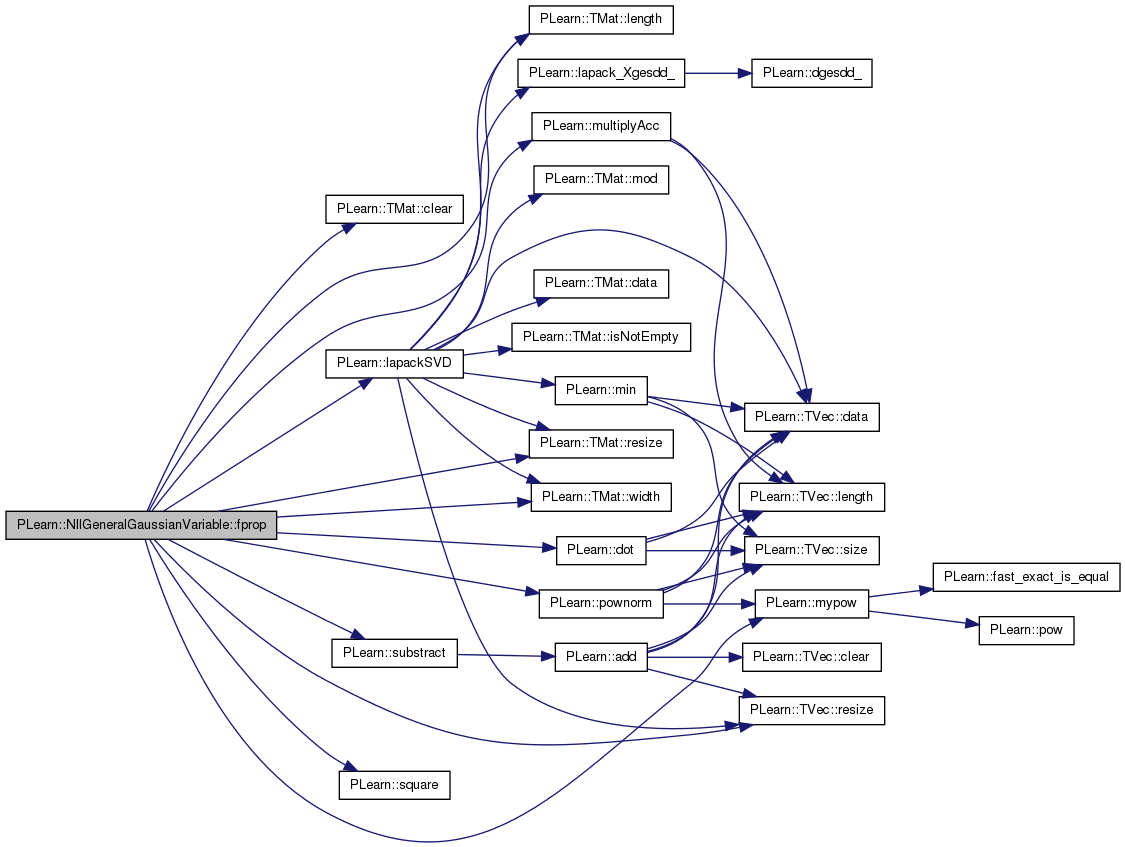
| void PLearn::NllGeneralGaussianVariable::fprop | ( | ) | [virtual] |
compute output given input
Implements PLearn::Variable.
Definition at line 160 of file NllGeneralGaussianVariable.cc.
References PLearn::TMat< T >::clear(), diff_neighbor_input, PLearn::dot(), F, F_copy, fk, input, inv_Sigma_F, inv_sigma_fk, inv_Sigma_z, inv_sigma_zj, j, PLearn::lapackSVD(), PLearn::TMat< T >::length(), Log2Pi, mu, PLearn::multiplyAcc(), PLearn::mypow(), n, ncomponents, neighbors, nneighbors, pl_log, PLearn::pownorm(), PLearn::TVec< T >::resize(), PLearn::TMat< T >::resize(), S, sm_svd, sn, PLearn::square(), PLearn::substract(), tr_inv_Sigma, U, uk, uk2, use_mu, Ut, V, PLearn::Variable::value, PLearn::TMat< T >::width(), z, and zj.
{
F_copy.resize(F.length(),F.width());
sm_svd.resize(ncomponents);
// N.B. this is the SVD of F'
F_copy << F;
lapackSVD(F_copy, Ut, S, V,'A',1.5);
for (int k=0;k<ncomponents;k++)
{
sm_svd[k] = mypow(S[k],2);
U(k) << Ut(k);
}
real mahal = 0;
real norm_term = 0;
real dotp = 0;
real coef = 0;
inv_Sigma_z.clear();
tr_inv_Sigma = 0;
for(int j=0; j<nneighbors;j++)
{
zj = z(j);
if(use_mu)
{
substract(neighbors(j),input,diff_neighbor_input);
substract(diff_neighbor_input,mu,zj);
}
else
{
substract(neighbors(j),input,zj);
}
mahal = -0.5*pownorm(zj)/sn[0];
norm_term = - n/2.0 * Log2Pi - 0.5*(n-ncomponents)*pl_log(sn[0]);
inv_sigma_zj = inv_Sigma_z(j);
inv_sigma_zj << zj;
inv_sigma_zj /= sn[0];
if(j==0)
tr_inv_Sigma = n/sn[0];
for(int k=0; k<ncomponents; k++)
{
uk = U(k);
dotp = dot(zj,uk);
coef = (1.0/(sm_svd[k]+sn[0]) - 1.0/sn[0]);
multiplyAcc(inv_sigma_zj,uk,dotp*coef);
mahal -= square(dotp)*0.5*coef;
norm_term -= 0.5*pl_log(sm_svd[k]);
if(j==0)
tr_inv_Sigma += coef;
}
value[j] = -1*(norm_term + mahal);
}
inv_Sigma_F.clear();
for(int k=0; k<ncomponents; k++)
{
fk = F(k);
inv_sigma_fk = inv_Sigma_F(k);
inv_sigma_fk << fk;
inv_sigma_fk /= sn[0];
for(int k2=0; k2<ncomponents;k2++)
{
uk2 = U(k2);
multiplyAcc(inv_sigma_fk,uk2,
(1.0/(sm_svd[k2]+sn[0]) - 1.0/sn[0])*dot(fk,uk2));
}
}
}
| OptionList & PLearn::NllGeneralGaussianVariable::getOptionList | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 71 of file NllGeneralGaussianVariable.cc.
| OptionMap & PLearn::NllGeneralGaussianVariable::getOptionMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 71 of file NllGeneralGaussianVariable.cc.
| RemoteMethodMap & PLearn::NllGeneralGaussianVariable::getRemoteMethodMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 71 of file NllGeneralGaussianVariable.cc.
| void PLearn::NllGeneralGaussianVariable::makeDeepCopyFromShallowCopy | ( | CopiesMap & | copies | ) | [virtual] |
Does the necessary operations to transform a shallow copy (this) into a deep copy by deep-copying all the members that need to be.
This needs to be overridden by every class that adds "complex" data members to the class, such as Vec, Mat, PP<Something>, etc. Typical implementation:
void CLASS_OF_THIS::makeDeepCopyFromShallowCopy(CopiesMap& copies) { inherited::makeDeepCopyFromShallowCopy(copies); deepCopyField(complex_data_member1, copies); deepCopyField(complex_data_member2, copies); ... }
| copies | A map used by the deep-copy mechanism to keep track of already-copied objects. |
Reimplemented from PLearn::NaryVariable.
Definition at line 291 of file NllGeneralGaussianVariable.cc.
References PLearn::deepCopyField(), diff_neighbor_input, F, F_copy, fk, input, inv_Sigma_F, inv_sigma_fk, inv_Sigma_z, inv_sigma_zj, mu, neighbors, S, sm_svd, sn, temp_ncomp, U, uk, uk2, Ut, V, z, and zj.
{
NaryVariable::makeDeepCopyFromShallowCopy(copies);
deepCopyField(input, copies);
deepCopyField(neighbors, copies);
deepCopyField(diff_neighbor_input, copies);
deepCopyField(mu, copies);
deepCopyField(sm_svd, copies);
deepCopyField(sn, copies);
deepCopyField(S, copies);
deepCopyField(uk, copies);
deepCopyField(fk, copies);
deepCopyField(uk2, copies);
deepCopyField(inv_sigma_zj, copies);
deepCopyField(zj, copies);
deepCopyField(inv_sigma_fk, copies);
deepCopyField(temp_ncomp, copies);
deepCopyField(F, copies);
deepCopyField(F_copy, copies);
deepCopyField(z, copies);
deepCopyField(U, copies);
deepCopyField(Ut, copies);
deepCopyField(V, copies);
deepCopyField(inv_Sigma_F, copies);
deepCopyField(inv_Sigma_z, copies);
}

Recomputes the length l and width w that this variable should have, according to its parent variables.
This is used for ex. by sizeprop() The default version stupidly returns the current dimensions, so make sure to overload it in subclasses if this is not appropriate.
Reimplemented from PLearn::Variable.
Definition at line 154 of file NllGeneralGaussianVariable.cc.
References PLearn::TVec< T >::length(), and PLearn::NaryVariable::varray.
{
len = varray[4]->length();
wid = 1;
}

| void PLearn::NllGeneralGaussianVariable::symbolicBprop | ( | ) | [virtual] |
compute a piece of new Var graph that represents the symbolic derivative of this Var
Reimplemented from PLearn::Variable.
Definition at line 286 of file NllGeneralGaussianVariable.cc.
References PLERROR.
{
PLERROR("In NllGeneralGaussianVariable::symbolicBprop(): Not implemented");
}
Reimplemented from PLearn::NaryVariable.
Definition at line 83 of file NllGeneralGaussianVariable.h.
Definition at line 61 of file NllGeneralGaussianVariable.h.
Referenced by build_(), fprop(), and makeDeepCopyFromShallowCopy().
Mat PLearn::NllGeneralGaussianVariable::F [protected] |
Definition at line 64 of file NllGeneralGaussianVariable.h.
Referenced by bprop(), build_(), fprop(), and makeDeepCopyFromShallowCopy().
Mat PLearn::NllGeneralGaussianVariable::F_copy [protected] |
Definition at line 64 of file NllGeneralGaussianVariable.h.
Referenced by fprop(), and makeDeepCopyFromShallowCopy().
Vec PLearn::NllGeneralGaussianVariable::fk [protected] |
Definition at line 62 of file NllGeneralGaussianVariable.h.
Referenced by fprop(), and makeDeepCopyFromShallowCopy().
Vec PLearn::NllGeneralGaussianVariable::input [protected] |
Temporary storage variables.
Definition at line 61 of file NllGeneralGaussianVariable.h.
Referenced by build_(), fprop(), and makeDeepCopyFromShallowCopy().
Mat PLearn::NllGeneralGaussianVariable::inv_Sigma_F [protected] |
Definition at line 64 of file NllGeneralGaussianVariable.h.
Referenced by bprop(), build_(), fprop(), and makeDeepCopyFromShallowCopy().
Vec PLearn::NllGeneralGaussianVariable::inv_sigma_fk [protected] |
Definition at line 62 of file NllGeneralGaussianVariable.h.
Referenced by fprop(), and makeDeepCopyFromShallowCopy().
Mat PLearn::NllGeneralGaussianVariable::inv_Sigma_z [protected] |
Definition at line 64 of file NllGeneralGaussianVariable.h.
Referenced by bprop(), build_(), fprop(), and makeDeepCopyFromShallowCopy().
Vec PLearn::NllGeneralGaussianVariable::inv_sigma_zj [protected] |
Definition at line 62 of file NllGeneralGaussianVariable.h.
Referenced by fprop(), and makeDeepCopyFromShallowCopy().
Log of number of components L.
Definition at line 68 of file NllGeneralGaussianVariable.h.
Referenced by bprop().
Vec PLearn::NllGeneralGaussianVariable::mu [protected] |
Definition at line 61 of file NllGeneralGaussianVariable.h.
Referenced by build_(), fprop(), and makeDeepCopyFromShallowCopy().
Number of nearest neighbors to learn mu, which must be < then nneighbors.
Definition at line 75 of file NllGeneralGaussianVariable.h.
int PLearn::NllGeneralGaussianVariable::n [protected] |
Dimensionality of the input vectors.
Definition at line 52 of file NllGeneralGaussianVariable.h.
int PLearn::NllGeneralGaussianVariable::ncomponents [protected] |
Number of components (i.e. number of vectors in f)
Definition at line 54 of file NllGeneralGaussianVariable.h.
Mat PLearn::NllGeneralGaussianVariable::neighbors [protected] |
Definition at line 64 of file NllGeneralGaussianVariable.h.
Referenced by build_(), fprop(), and makeDeepCopyFromShallowCopy().
int PLearn::NllGeneralGaussianVariable::nneighbors [protected] |
Number of nearest neighbors.
Definition at line 56 of file NllGeneralGaussianVariable.h.
Vec PLearn::NllGeneralGaussianVariable::S [protected] |
Definition at line 61 of file NllGeneralGaussianVariable.h.
Referenced by fprop(), and makeDeepCopyFromShallowCopy().
Vec PLearn::NllGeneralGaussianVariable::sm_svd [protected] |
Definition at line 61 of file NllGeneralGaussianVariable.h.
Referenced by fprop(), and makeDeepCopyFromShallowCopy().
Vec PLearn::NllGeneralGaussianVariable::sn [protected] |
Definition at line 61 of file NllGeneralGaussianVariable.h.
Referenced by build_(), fprop(), and makeDeepCopyFromShallowCopy().
Vec PLearn::NllGeneralGaussianVariable::temp_ncomp [protected] |
Definition at line 63 of file NllGeneralGaussianVariable.h.
Referenced by bprop(), build_(), and makeDeepCopyFromShallowCopy().
real PLearn::NllGeneralGaussianVariable::tr_inv_Sigma [protected] |
Trace of the inverse of the covariance matrix.
Definition at line 58 of file NllGeneralGaussianVariable.h.
Mat PLearn::NllGeneralGaussianVariable::U [protected] |
Definition at line 64 of file NllGeneralGaussianVariable.h.
Referenced by build_(), fprop(), and makeDeepCopyFromShallowCopy().
Vec PLearn::NllGeneralGaussianVariable::uk [protected] |
Definition at line 62 of file NllGeneralGaussianVariable.h.
Referenced by fprop(), and makeDeepCopyFromShallowCopy().
Vec PLearn::NllGeneralGaussianVariable::uk2 [protected] |
Definition at line 62 of file NllGeneralGaussianVariable.h.
Referenced by fprop(), and makeDeepCopyFromShallowCopy().
Indication that a parameter corresponding to the difference between the Gaussian center and the input data point position should be used.
Definition at line 72 of file NllGeneralGaussianVariable.h.
Mat PLearn::NllGeneralGaussianVariable::Ut [protected] |
Definition at line 64 of file NllGeneralGaussianVariable.h.
Referenced by build_(), fprop(), and makeDeepCopyFromShallowCopy().
Mat PLearn::NllGeneralGaussianVariable::V [protected] |
Definition at line 64 of file NllGeneralGaussianVariable.h.
Referenced by build_(), fprop(), and makeDeepCopyFromShallowCopy().
Mat PLearn::NllGeneralGaussianVariable::z [protected] |
Definition at line 64 of file NllGeneralGaussianVariable.h.
Referenced by build_(), fprop(), and makeDeepCopyFromShallowCopy().
Vec PLearn::NllGeneralGaussianVariable::zj [protected] |
Definition at line 62 of file NllGeneralGaussianVariable.h.
Referenced by fprop(), and makeDeepCopyFromShallowCopy().
 1.7.4
1.7.4