|
PLearn 0.1
|
|
PLearn 0.1
|
Computes a cost function for a (hidden) representation. More...
#include <LayerCostModule.h>
Public Member Functions | |
| LayerCostModule () | |
| Default constructor. | |
| virtual void | fprop (const Vec &input, real &cost) const |
| given the input and target, compute the cost | |
| virtual void | fprop (const Mat &inputs, Mat &costs) const |
| virtual void | fprop (const Mat &inputs, const Mat &targets, Mat &costs) const |
| Mini-batch version with several costs.. | |
| virtual void | fprop (const TVec< Mat * > &ports_value) |
| Overridden to try to use the standard mini-batch fprop when possible. | |
| virtual void | bpropUpdate (const Mat &inputs, const Mat &targets, const Vec &costs, Mat &input_gradients, bool accumulate=false) |
| backpropagate the derivative w.r.t. activation | |
| virtual void | bpropUpdate (const Mat &inputs, Mat &inputs_grad) |
| important NOTE: the normalization by one_count = 1 / n_samples is supposed to be done in the OnlineLearningModules updates ( cf. | |
| virtual void | bpropAccUpdate (const TVec< Mat * > &ports_value, const TVec< Mat * > &ports_gradient) |
| Overridden to try to use the standard mini-batch bprop when possible. | |
| virtual void | computeHisto (const Mat &inputs) |
| Some auxiliary function to deal with empirical histograms. | |
| virtual void | computeHisto (const Mat &inputs, Mat &histo) const |
| virtual real | delta_KLdivTerm (int i, int j, int index_i, real over_dq) |
| virtual real | KLdivTerm (real pi, real pj) const |
| virtual real | computeKLdiv (bool store_in_cache) |
| virtual real | computeKLdiv (const Mat &histo) const |
| virtual int | histo_index (real q) const |
| virtual real | dq (real q) const |
| virtual void | computeSafeHisto (const Mat &inputs) |
| Auxiliary functions for kl_div_simple cost function. | |
| virtual void | computeSafeHisto (const Mat &inputs, Mat &histo) const |
| virtual real | delta_SafeKLdivTerm (int i, int j, int index_i, real over_dq) |
| virtual void | computePascalStatistics (const Mat &inputs) |
| Auxiliary function for the pascal's cost function. | |
| virtual void | computePascalStatistics (const Mat &inputs, Vec &expectation, Mat &cross_quadratic_mean) const |
| virtual real | func_ (real correlation) const |
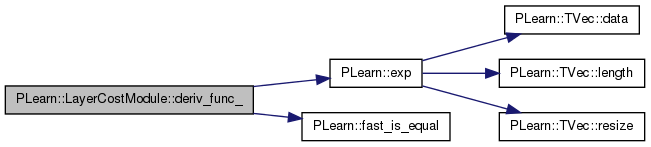
| virtual real | deriv_func_ (real correlation) const |
| virtual void | computeCorrelationStatistics (const Mat &inputs) |
| Auxiliary function for the correlation's cost function. | |
| virtual void | computeCorrelationStatistics (const Mat &inputs, Vec &expectation, Mat &cross_quadratic_mean, Vec &stds, Mat &correlations) const |
| CAUTION: Be careful 'cross_quadratic_mean' and 'correlations' matrices are computed ONLY on the triangle subpart 'i'>='j' if we note 'i' (resp. | |
| virtual const TVec< string > & | getPorts () |
| Returns all ports in a RBMModule. | |
| virtual const TMat< int > & | getPortSizes () |
| The ports' sizes are given by the corresponding RBM layers. | |
| virtual int | getPortIndex (const string &port) |
| Return the index (as in the list of ports returned by getPorts()) of a given port. | |
| virtual void | setLearningRate (real dynamic_learning_rate) |
| Overridden to do nothing (in particular, no warning). | |
| virtual TVec< string > | costNames () |
| Indicates the name of the computed costs. | |
| virtual string | classname () const |
| virtual OptionList & | getOptionList () const |
| virtual OptionMap & | getOptionMap () const |
| virtual RemoteMethodMap & | getRemoteMethodMap () const |
| virtual LayerCostModule * | deepCopy (CopiesMap &copies) const |
| virtual void | build () |
| Post-constructor. | |
| virtual void | makeDeepCopyFromShallowCopy (CopiesMap &copies) |
| Transforms a shallow copy into a deep copy. | |
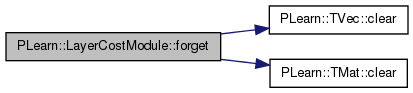
| virtual void | forget () |
| reset the parameters to the state they would be BEFORE starting training. | |
Static Public Member Functions | |
| static string | _classname_ () |
| static OptionList & | _getOptionList_ () |
| static RemoteMethodMap & | _getRemoteMethodMap_ () |
| static Object * | _new_instance_for_typemap_ () |
| static bool | _isa_ (const Object *o) |
| static void | _static_initialize_ () |
| static const PPath & | declaringFile () |
Public Attributes | |
| string | cost_function |
| Generic name of the cost function. | |
| int | nstages_max |
| Maximum number of stages we want to propagate the gradient. | |
| real | momentum |
| Parameter to compute moving means in non stochastic cost functions. | |
| string | optimization_strategy |
| Kind of optimization. | |
| real | alpha |
| Parameter in pascal's cost function. | |
| int | histo_size |
| For non stochastic KL divergence cost function. | |
| Mat | inputs_histo |
| Histograms of inputs (estimated empiricially on some data) Computed only when cost_function == 'kl_div' or 'kl_div_simpe'. | |
| Vec | inputs_expectation |
| Statistics on inputs (estimated empiricially on some data) Computed only when cost_function == 'correlation' or (for some) 'pascal'. | |
| Vec | inputs_stds |
| Mat | inputs_cross_quadratic_mean |
| only for 'correlation' cost function | |
| Mat | inputs_correlations |
| Vec | inputs_expectation_trainMemory |
| only for 'correlation' cost function | |
| Mat | inputs_cross_quadratic_mean_trainMemory |
| string | penalty_function |
| The function applied to the local cost between 2 inputs to obtain the global cost (after averaging) | |
| string | cost_function_completename |
| The generic name of the cost function. | |
Static Public Attributes | |
| static StaticInitializer | _static_initializer_ |
Protected Member Functions | |
| void | addPortName (const string &name) |
| Add a new port to the 'portname_to_index' map and 'ports' vector. | |
Static Protected Member Functions | |
| static void | declareOptions (OptionList &ol) |
| Declares the class options. | |
Protected Attributes | |
| bool | LINEAR_FUNC |
| bool | SQUARE_FUNC |
| bool | POW4_FUNC |
| bool | EXP_FUNC |
| bool | LOG_FUNC |
| int | stage |
| Number of stage the BPropAccUpdate function was called. | |
| bool | bprop_all_terms |
| Boolean determined by the optimization_strategy. | |
| bool | random_index_during_bprop |
| bool | is_cost_function_stochastic |
| Does stochastic gradient (without memory of the past) makes sense with our cost function? | |
| real | norm_factor |
| Normalizing factor applied to the cost function to take into acount the number of weights. | |
| real | average_deriv |
| real | HISTO_STEP |
| Variables for (non stochastic) KL Div cost function. | |
| real | one_count |
| the weight of a sample within a batch (usually, 1/n_samples) | |
| TVec< TVec< Vec > > | cache_differ_count_i |
| TVec< TVec< Vec > > | cache_differ_count_j |
| TVec< TVec< Vec > > | cache_n_differ |
| map< string, int > | portname_to_index |
| Map from a port name to its index in the 'ports' vector. | |
| TVec< string > | ports |
| List of port names. | |
Private Types | |
| typedef CostModule | inherited |
Private Member Functions | |
| void | build_ () |
| This does the actual building. | |
Computes a cost function for a (hidden) representation.
Backpropagates it.
Definition at line 51 of file LayerCostModule.h.
typedef CostModule PLearn::LayerCostModule::inherited [private] |
Reimplemented from PLearn::CostModule.
Definition at line 53 of file LayerCostModule.h.
| PLearn::LayerCostModule::LayerCostModule | ( | ) |
Default constructor.
Definition at line 56 of file LayerCostModule.cc.
References PLearn::OnlineLearningModule::output_size.
:
cost_function("correlation"),
nstages_max(-1),
momentum(0.),
optimization_strategy("standard"),
alpha(0.),
histo_size(10),
penalty_function("square"),
cost_function_completename(""),
stage(0),
bprop_all_terms(true),
random_index_during_bprop(false),
average_deriv(0.)
{
output_size = 1;
}
| string PLearn::LayerCostModule::_classname_ | ( | ) | [static] |
Reimplemented from PLearn::CostModule.
Definition at line 54 of file LayerCostModule.cc.
: some are valid only for binomial layers. \n");
| OptionList & PLearn::LayerCostModule::_getOptionList_ | ( | ) | [static] |
Reimplemented from PLearn::CostModule.
Definition at line 54 of file LayerCostModule.cc.
: some are valid only for binomial layers. \n");
| RemoteMethodMap & PLearn::LayerCostModule::_getRemoteMethodMap_ | ( | ) | [static] |
Reimplemented from PLearn::CostModule.
Definition at line 54 of file LayerCostModule.cc.
: some are valid only for binomial layers. \n");
Reimplemented from PLearn::CostModule.
Definition at line 54 of file LayerCostModule.cc.
: some are valid only for binomial layers. \n");
| Object * PLearn::LayerCostModule::_new_instance_for_typemap_ | ( | ) | [static] |
Reimplemented from PLearn::CostModule.
Definition at line 54 of file LayerCostModule.cc.
: some are valid only for binomial layers. \n");
| StaticInitializer LayerCostModule::_static_initializer_ & PLearn::LayerCostModule::_static_initialize_ | ( | ) | [static] |
Reimplemented from PLearn::CostModule.
Definition at line 54 of file LayerCostModule.cc.
: some are valid only for binomial layers. \n");
| void PLearn::LayerCostModule::addPortName | ( | const string & | name | ) | [protected] |
Add a new port to the 'portname_to_index' map and 'ports' vector.
Definition at line 1594 of file LayerCostModule.cc.
References PLearn::TVec< T >::append(), PLearn::TVec< T >::length(), PLearn::OnlineLearningModule::name, PLASSERT, portname_to_index, and ports.
Referenced by build_().
{
PLASSERT( portname_to_index.find(name) == portname_to_index.end() );
portname_to_index[name] = ports.length();
ports.append(name);
}


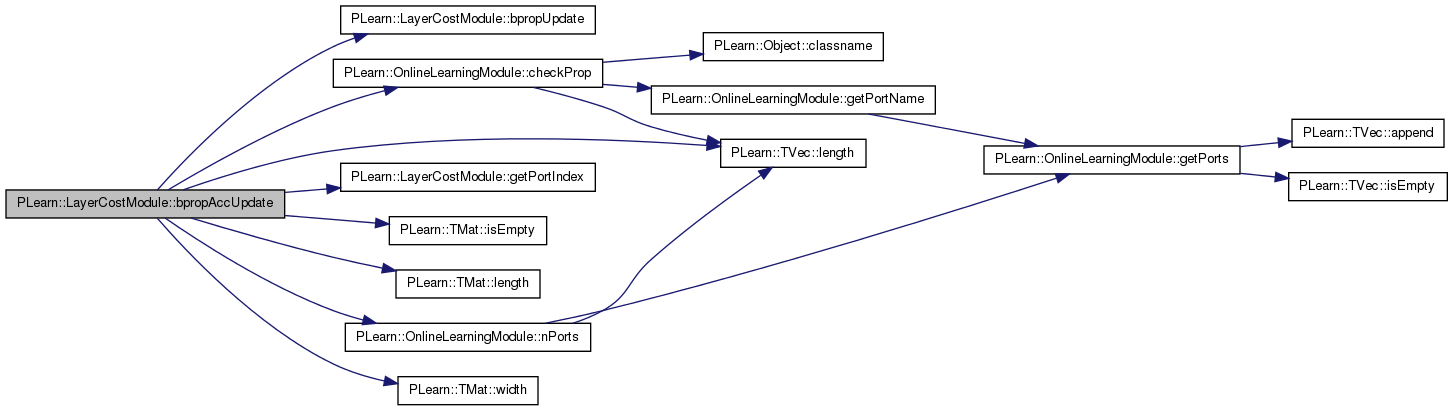
| void PLearn::LayerCostModule::bpropAccUpdate | ( | const TVec< Mat * > & | ports_value, |
| const TVec< Mat * > & | ports_gradient | ||
| ) | [virtual] |
Overridden to try to use the standard mini-batch bprop when possible.
Reimplemented from PLearn::CostModule.
Definition at line 594 of file LayerCostModule.cc.
References bpropUpdate(), PLearn::OnlineLearningModule::checkProp(), getPortIndex(), i, PLearn::OnlineLearningModule::input_size, PLearn::TMat< T >::isEmpty(), PLearn::TMat< T >::length(), PLearn::TVec< T >::length(), PLearn::OnlineLearningModule::nPorts(), PLASSERT, PLERROR, and PLearn::TMat< T >::width().
{
PLASSERT( input_size > 1 );
PLASSERT( ports_value.length() == nPorts() );
PLASSERT( ports_gradient.length() == nPorts() );
const Mat* p_inputs = ports_value[getPortIndex("input")];
Mat* p_inputs_grad = ports_gradient[getPortIndex("input")];
Mat* p_cost_grad = ports_gradient[getPortIndex("cost")];
if( p_inputs_grad && p_inputs_grad->isEmpty()
&& p_cost_grad && !p_cost_grad->isEmpty() )
{
PLASSERT( p_inputs && !p_inputs->isEmpty());
int n_samples = p_inputs->length();
PLASSERT( p_cost_grad->length() == n_samples );
PLASSERT( p_cost_grad->width() == 1 );
bpropUpdate( *p_inputs, *p_inputs_grad);
for( int isample = 0; isample < n_samples; isample++ )
for( int i = 0; i < input_size; i++ )
(*p_inputs_grad)(isample, i) *= (*p_cost_grad)(isample,0);
checkProp(ports_gradient);
}
else if( !p_inputs_grad && !p_cost_grad )
return;
else
PLERROR("In LayerCostModule::bpropAccUpdate - Port configuration not implemented.");
}
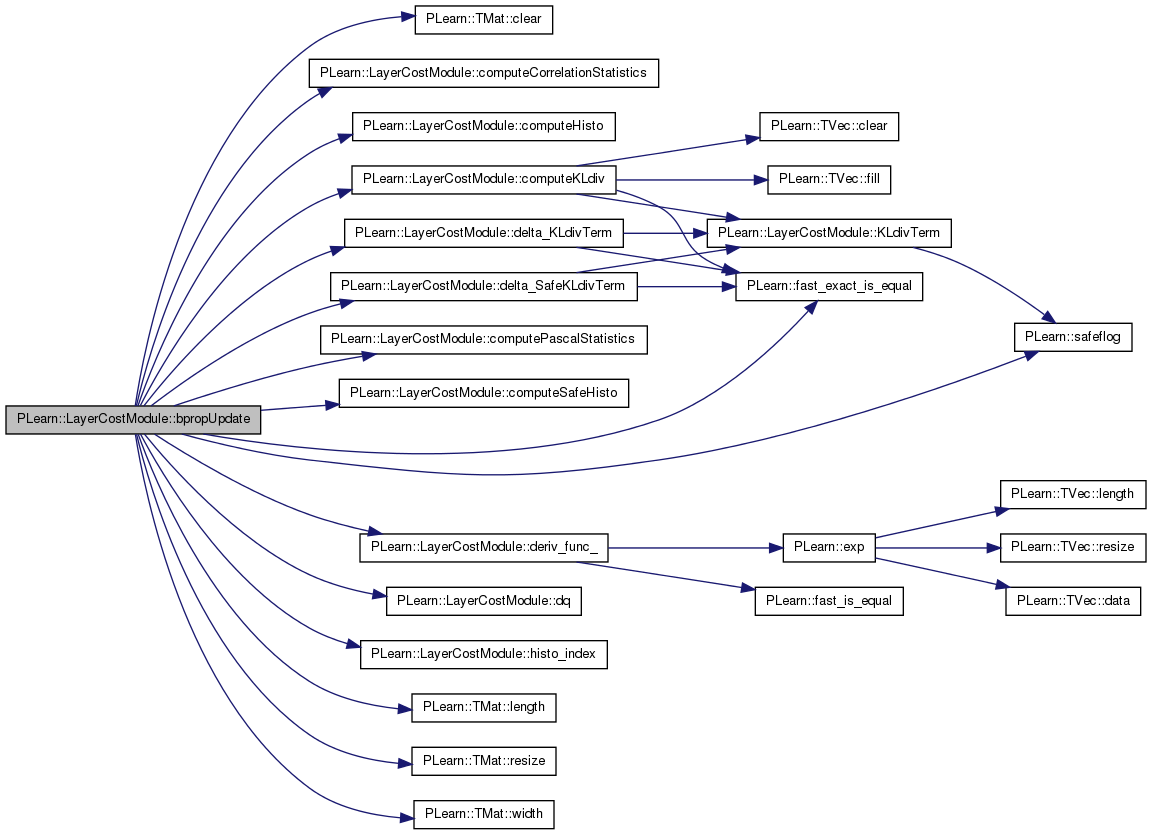
| void PLearn::LayerCostModule::bpropUpdate | ( | const Mat & | inputs, |
| const Mat & | targets, | ||
| const Vec & | costs, | ||
| Mat & | input_gradients, | ||
| bool | accumulate = false |
||
| ) | [virtual] |
backpropagate the derivative w.r.t. activation
Reimplemented from PLearn::CostModule.
Definition at line 586 of file LayerCostModule.cc.
Referenced by bpropAccUpdate().
{
bpropUpdate( inputs, inputs_grad);
}

important NOTE: the normalization by one_count = 1 / n_samples is supposed to be done in the OnlineLearningModules updates ( cf.
RBMMatrixConnection::bpropUpdate(), RBMBinomialLayer::bpropUpdate() in the batch version, etc. )
dCROSSij_dqj[i] = d[ E(QiQj)-E(Qi)E(Qj) ]/d[qj(t)] = ( qi(t) - E(Qi) ) / n_samples
dSTDi_dqi[i] = d[ STD(Qi) ]/d[qi(t)] = d[ sqrt( E(Qi^2) -E(Qi)^2 ]/d[qi(t)] = 1 / [ 2.STD(Qi) ] * d[ E(Qi^2) -E(Qi)^2 ]/d[qi(t)] = 1 / [ 2.STD(Qi) ] * [ 2*qi(t) / n_samples - 2*E(Qi) / n_samples ] = ( qi(t) - E(Qi) ) / ( n_samples * STD(Qi) ) = dCROSSij_dqj[i] / STD(Qi)
Definition at line 631 of file LayerCostModule.cc.
References alpha, average_deriv, bprop_all_terms, PLearn::TMat< T >::clear(), computeCorrelationStatistics(), computeHisto(), computeKLdiv(), computePascalStatistics(), computeSafeHisto(), cost_function, delta_KLdivTerm(), delta_SafeKLdivTerm(), deriv_func_(), dq(), PLearn::fast_exact_is_equal(), histo_index(), histo_size, i, PLearn::OnlineLearningModule::input_size, inputs_correlations, inputs_cross_quadratic_mean, inputs_expectation, inputs_stds, j, PLearn::TMat< T >::length(), momentum, norm_factor, nstages_max, PLASSERT, PLERROR, PLWARNING, random_index_during_bprop, PLearn::TMat< T >::resize(), PLearn::safeflog(), stage, and PLearn::TMat< T >::width().
{
if( random_index_during_bprop )
PLERROR("LayerCostModule::bpropUpdate with random_index_during_bprop not implemented yet.");
PLASSERT( inputs.width() == input_size );
inputs_grad.resize(inputs.length(), input_size );
inputs_grad.clear();
int n_samples = inputs.length();
inputs_grad.resize(n_samples, input_size);
inputs_grad.clear();
stage += n_samples;
if( (nstages_max>0) && (stage > nstages_max) )
return;
//cout << "bpropAccUpdate" << endl;
if( cost_function == "stochastic_cross_entropy" )
{
for (int isample = 0; isample < n_samples; isample++)
{
real qi, qj, comp_qi, comp_qj;
Vec comp_q(input_size), log_term(input_size);
for (int i = 0 ; i < input_size ; i++ )
{
qi = inputs(isample,i);
comp_qi = 1.0 - qi;
comp_q[i] = comp_qi;
log_term[i] = safeflog(qi) - safeflog(comp_qi);
}
for (int i = 0; i < input_size; i++ )
{
qi = inputs(isample,i);
comp_qi = comp_q[i];
for (int j = 0; j < i; j++ )
{
qj = inputs(isample,j);
comp_qj=comp_q[j];
// log(pj) - log(1-pj) + pj/pi - (1-pj)/(1-pi)
inputs(isample,i) += log_term[j] + qj/qi - comp_qi/comp_qj;
// The symetric part (loop j=i+1...input_size)
if( bprop_all_terms )
inputs(isample,j) += log_term[i] + qi/qj - comp_qj/comp_qi;
}
}
for (int i = 0; i < input_size; i++ )
inputs_grad(isample, i) *= norm_factor;
}
} // END cost_function == "stochastic_cross_entropy"
else if( cost_function == "stochastic_kl_div" )
{
for (int isample = 0; isample < n_samples; isample++)
{
real qi, qj, comp_qi, comp_qj;
Vec comp_q(input_size), log_term(input_size);
for (int i = 0; i < input_size; i++ )
{
qi = inputs(isample,i);
comp_qi = 1.0 - qi;
if(fast_exact_is_equal(qi, 1.0) || fast_exact_is_equal(qi, 0.0))
comp_q[i] = REAL_MAX;
else
comp_q[i] = 1.0/(qi*comp_qi);
log_term[i] = safeflog(qi) - safeflog(comp_qi);
}
for (int i = 0; i < input_size; i++ )
{
qi = inputs(isample,i);
comp_qi = comp_q[i];
for (int j = 0; j < i ; j++ )
{
qj = inputs(isample,j);
comp_qj=comp_q[j];
// [qj - qi]/[qi (1-qi)] - log[ qi/(1-qi) * (1-qj)/qj]
inputs_grad(isample,i) += (qj - qi)*comp_qi - log_term[i] + log_term[j];
// The symetric part (loop j=i+1...input_size)
if( bprop_all_terms )
inputs_grad(isample,j) += (qi - qj)*comp_qj - log_term[j] + log_term[i];
}
}
for (int i = 0; i < input_size; i++ )
inputs_grad(isample, i) *= norm_factor;
}
} // END cost_function == "stochastic_kl_div"
else if( cost_function == "kl_div" )
{
computeHisto(inputs);
real cost_before = computeKLdiv( true );
if( !bprop_all_terms )
PLERROR("kl_div with bprop_all_terms=false not implemented yet");
for (int isample = 0; isample < n_samples; isample++)
{
real qi, qj;
// Computing the difference of KL divergence
// for d_q
for (int i = 0; i < input_size; i++)
{
qi=inputs(isample,i);
if( histo_index(qi) < histo_size-1 )
{
inputs(isample,i) += dq(qi);
computeHisto(inputs);
real cost_after = computeKLdiv( false );
inputs(isample,i) -= dq(qi);
inputs_grad(isample, i) = (cost_after - cost_before)*1./dq(qi);
}
//else inputs_grad(isample, i) = 0.;
continue;
inputs_grad(isample, i) = 0.;
qi = inputs(isample,i);
int index_i = histo_index(qi);
if( ( index_i == histo_size-1 ) ) // we do not care about this...
continue;
real over_dqi=1.0/dq(qi);
// qi + dq(qi) ==> | p_inputs_histo(i,index_i) - one_count
// \ p_inputs_histo(i,index_i+shift_i) + one_count
for (int j = 0; j < i; j++)
{
inputs_grad(isample, i) += delta_KLdivTerm(i, j, index_i, over_dqi);
qj = inputs(isample,j);
int index_j = histo_index(qj);
if( ( index_j == histo_size-1 ) )
continue;
real over_dqj=1.0/dq(qj);
// qj + dq(qj) ==> | p_inputs_histo(j,index_j) - one_count
// \ p_inputs_histo(j,index_j+shift_j) + one_count
inputs_grad(isample, j) += delta_KLdivTerm(j, i, index_j, over_dqj);
}
}
}
} // END cost_function == "kl_div"
else if( cost_function == "kl_div_simple" )
{
computeSafeHisto(inputs);
for (int isample = 0; isample < n_samples; isample++)
{
// Computing the difference of KL divergence
// for d_q
real qi, qj;
for (int i = 0; i < input_size; i++)
{
inputs_grad(isample, i) = 0.0;
qi = inputs(isample,i);
int index_i = histo_index(qi);
if( ( index_i == histo_size-1 ) ) // we do not care about this...
continue;
real over_dqi=1.0/dq(qi);
// qi + dq(qi) ==> | p_inputs_histo(i,index_i) - one_count
// \ p_inputs_histo(i,index_i+shift_i) + one_count
for (int j = 0; j < i; j++)
{
inputs_grad(isample, i) += delta_SafeKLdivTerm(i, j, index_i, over_dqi);
if( bprop_all_terms )
{
qj = inputs(isample,j);
int index_j = histo_index(qj);
if( ( index_j == histo_size-1 ) || ( index_j == 0 ) )
continue;
real over_dqj=1.0/dq(qj);
// qj + dq(qj) ==> | p_inputs_histo(j,index_j) - one_count
// \ p_inputs_histo(j,index_j+shift_j) + one_count
inputs_grad(isample, j) += delta_SafeKLdivTerm(j, i, index_j, over_dqj);
}
}
}
// Normalization
for (int i = 0; i < input_size; i++ )
inputs_grad(isample, i) *= norm_factor;
}
} // END cost_function == "kl_div simple"
else if( cost_function == "pascal" )
{
computePascalStatistics( inputs );
for (int isample = 0; isample < n_samples; isample++)
{
real qi, qj;
for (int i = 0; i < input_size; i++)
{
qi = inputs(isample, i);
if (alpha > 0.0 )
inputs_grad(isample, i) -= alpha*deriv_func_(inputs_expectation[i])
*(real)(input_size-1);
for (int j = 0; j < i; j++)
{
real d_temp = deriv_func_(inputs_cross_quadratic_mean(i,j));
qj = inputs(isample,j);
inputs_grad(isample, i) += d_temp *qj;
if( bprop_all_terms )
inputs_grad(isample, j) += d_temp *qi;
}
}
for (int i = 0; i < input_size; i++)
inputs_grad(isample, i) *= norm_factor * (1.-momentum);
}
} // END cost_function == "pascal"
else if( cost_function == "correlation")
{
computeCorrelationStatistics( inputs );
real average_deriv_tmp = 0.;
for (int isample = 0; isample < n_samples; isample++)
{
real qi, qj;
Vec dSTDi_dqi( input_size ), dCROSSij_dqj( input_size );
for (int i = 0; i < input_size; i++)
{
if( fast_exact_is_equal( inputs_stds[i], 0. ) )
{
if( isample == 0 )
PLWARNING("wired phenomenon: the %dth output have always expectation %f ( at stage=%d )",
i, inputs_expectation[i], stage);
if( inputs_expectation[i] < 0.1 )
{
// We force to switch on the neuron
// (the cost increase much when the expectation is decreased \ 0)
if( ( isample > 0 ) || ( n_samples == 1 ) )
inputs_grad(isample, i) -= average_deriv;
}
else if( inputs_expectation[i] > 0.9 )
{
// We force to switch off the neuron
// (the cost increase much when we the expectation is increased / 1)
// except for the first sample
if( ( isample > 0 ) || ( n_samples == 1 ) )
inputs_grad(isample, i) += average_deriv;
}
else
if ( !(inputs_expectation[i]>-REAL_MAX) || !(inputs_expectation[i]<REAL_MAX) )
PLERROR("The %dth output have always value %f ( at stage=%d )",
i, inputs_expectation[i], stage);
continue;
}
qi = inputs(isample, i);
dCROSSij_dqj[i] = ( qi - inputs_expectation[i] ); //*one_count;
dSTDi_dqi[i] = dCROSSij_dqj[i] / inputs_stds[i];
for (int j = 0; j < i; j++)
{
if( fast_exact_is_equal( inputs_correlations(i,j), 0.) )
{
if (isample == 0)
PLWARNING("correlation(i,j)=0 for i=%d, j=%d", i, j);
continue;
}
qj = inputs(isample,j);
real correlation_denum = inputs_stds[i]*inputs_stds[j];
real squared_correlation_denum = correlation_denum * correlation_denum;
if( fast_exact_is_equal( squared_correlation_denum, 0. ) )
continue;
real dfunc_dCorr = deriv_func_( inputs_correlations(i,j) );
real correlation_num = ( inputs_cross_quadratic_mean(i,j)
- inputs_expectation[i]*inputs_expectation[j] );
if( correlation_num/correlation_denum - inputs_correlations(i,j) > 0.0000001 )
PLERROR( "num/denum (%f) <> correlation (%f) for (i,j)=(%d,%d)",
correlation_num/correlation_denum, inputs_correlations(i,j),i,j);
inputs_grad(isample, i) += dfunc_dCorr * (
correlation_denum * dCROSSij_dqj[j]
- correlation_num * dSTDi_dqi[i] * inputs_stds[j]
) / squared_correlation_denum;
if( bprop_all_terms )
inputs_grad(isample, j) += dfunc_dCorr * (
correlation_denum * dCROSSij_dqj[i]
- correlation_num * dSTDi_dqi[j] * inputs_stds[i]
) / squared_correlation_denum;
}
}
for (int i = 0; i < input_size; i++)
{
average_deriv_tmp += fabs( inputs_grad(isample, i) );
inputs_grad(isample, i) *= norm_factor * (1.-momentum);
}
}
average_deriv = average_deriv_tmp / (real)( input_size * n_samples );
PLASSERT( average_deriv >= 0.);
} // END cost_function == "correlation"
else
PLERROR("LayerCostModule::bpropAccUpdate() not implemented for cost function %s",
cost_function.c_str());
}
| void PLearn::LayerCostModule::build | ( | ) | [virtual] |
Post-constructor.
The normal implementation should call simply inherited::build(), then this class's build_(). This method should be callable again at later times, after modifying some option fields to change the "architecture" of the object.
Reimplemented from PLearn::CostModule.
Definition at line 270 of file LayerCostModule.cc.
References PLearn::CostModule::build(), and build_().
{
inherited::build();
build_();
}
| void PLearn::LayerCostModule::build_ | ( | ) | [private] |
This does the actual building.
Reimplemented from PLearn::CostModule.
Definition at line 160 of file LayerCostModule.cc.
References addPortName(), PLearn::addprepostfix(), bprop_all_terms, cache_differ_count_i, cache_differ_count_j, cache_n_differ, cost_function, cost_function_completename, EXP_FUNC, PLearn::TMat< T >::fill(), getPortIndex(), histo_size, HISTO_STEP, i, PLearn::OnlineLearningModule::input_size, inputs_cross_quadratic_mean_trainMemory, inputs_expectation_trainMemory, inputs_histo, is_cost_function_stochastic, j, LINEAR_FUNC, LOG_FUNC, PLearn::lowerstring(), momentum, norm_factor, PLearn::OnlineLearningModule::nPorts(), optimization_strategy, penalty_function, PLASSERT, PLERROR, PLearn::OnlineLearningModule::port_sizes, portname_to_index, ports, POW4_FUNC, random_index_during_bprop, PLearn::TVec< T >::resize(), PLearn::TMat< T >::resize(), SQUARE_FUNC, and PLearn::string_ends_with().
Referenced by build().
{
PLASSERT( histo_size > 1 );
PLASSERT( momentum >= 0.);
PLASSERT( momentum < 1.);
if( input_size > 1 )
norm_factor = 1./(real)(input_size*(input_size-1));
optimization_strategy = lowerstring( optimization_strategy );
if( optimization_strategy == "" )
optimization_strategy = "standard";
if ( optimization_strategy == "half" )
bprop_all_terms = false;
else if ( optimization_strategy == "random_half" )
{
bprop_all_terms = false;
random_index_during_bprop = true;
}
else if ( optimization_strategy != "standard" )
PLERROR( "LayerCostModule::build() does not recognize"
"optimization_strategy '%s'", optimization_strategy.c_str() );
cost_function = lowerstring( cost_function );
// choose HERE the *default* cost function
if( cost_function == "" )
cost_function = "pascal";
if( ( cost_function_completename == "" ) || !string_ends_with(cost_function_completename, cost_function) )
cost_function_completename = string(cost_function);
// list HERE all *stochastic* cost functions
if( ( cost_function == "stochastic_cross_entropy" )
|| ( cost_function == "stochastic_kl_div" ) )
is_cost_function_stochastic = true;
// list HERE all *non stochastic* cost functions
// and the specific initialization
else if( ( cost_function == "kl_div" )
|| ( cost_function == "kl_div_simple" ) )
{
is_cost_function_stochastic = false;
if( input_size > 0 )
inputs_histo.resize(input_size,histo_size);
HISTO_STEP = 1.0/(real)histo_size;
if( cost_function == "kl_div" )
{
cache_differ_count_i.resize(input_size);
cache_differ_count_j.resize(input_size);
cache_n_differ.resize(input_size);
for( int i = 0; i < input_size; i ++)
{
cache_differ_count_i[i].resize(i);
cache_differ_count_j[i].resize(i);
cache_n_differ[i].resize(i);
for( int j = 0; j < i; j ++)
{
cache_differ_count_i[i][j].resize(histo_size);
cache_differ_count_j[i][j].resize(histo_size);
cache_n_differ[i][j].resize(histo_size);
}
}
}
}
else if( ( cost_function == "pascal" )
|| ( cost_function == "correlation" ) )
{
is_cost_function_stochastic = false;
if( ( input_size > 0 ) && (momentum > 0.0) )
{
inputs_expectation_trainMemory.resize(input_size);
inputs_cross_quadratic_mean_trainMemory.resize(input_size,input_size);
}
cost_function_completename = addprepostfix( penalty_function, "_", cost_function );
LINEAR_FUNC = false;
SQUARE_FUNC = false;
POW4_FUNC = false;
EXP_FUNC = false;
LOG_FUNC = false;
penalty_function = lowerstring( penalty_function );
if( penalty_function == "linear" )
LINEAR_FUNC = true;
else if( penalty_function == "square" )
SQUARE_FUNC = true;
else if( penalty_function == "pow4" )
POW4_FUNC = true;
else if( penalty_function == "exp" )
EXP_FUNC = true;
else if( penalty_function == "log" )
LOG_FUNC = true;
else
PLERROR("LayerCostModule::build_() does not recognize penalty function '%s'",
penalty_function.c_str());
}
else
PLERROR("LayerCostModule::build_() does not recognize cost function '%s'",
cost_function.c_str());
// The port story...
ports.resize(0);
portname_to_index.clear();
addPortName("input");
addPortName("cost");
port_sizes.resize(nPorts(), 2);
port_sizes.fill(-1);
port_sizes(getPortIndex("input"), 1) = input_size;
port_sizes(getPortIndex("cost"), 1) = 1;
}

| string PLearn::LayerCostModule::classname | ( | ) | const [virtual] |
Reimplemented from PLearn::CostModule.
Definition at line 54 of file LayerCostModule.cc.
: some are valid only for binomial layers. \n");
| void PLearn::LayerCostModule::computeCorrelationStatistics | ( | const Mat & | inputs | ) | [virtual] |
Auxiliary function for the correlation's cost function.
Definition at line 1048 of file LayerCostModule.cc.
References inputs_correlations, inputs_cross_quadratic_mean, inputs_expectation, and inputs_stds.
Referenced by bpropUpdate(), and fprop().
{
computeCorrelationStatistics(inputs,
inputs_expectation, inputs_cross_quadratic_mean,
inputs_stds, inputs_correlations);
}

| void PLearn::LayerCostModule::computeCorrelationStatistics | ( | const Mat & | inputs, |
| Vec & | expectation, | ||
| Mat & | cross_quadratic_mean, | ||
| Vec & | stds, | ||
| Mat & | correlations | ||
| ) | const [virtual] |
CAUTION: Be careful 'cross_quadratic_mean' and 'correlations' matrices are computed ONLY on the triangle subpart 'i'>='j' if we note 'i' (resp.
'j') the first (reps.second) coordinate
Normalization (1/2)
Computation of the standard deviations requires temporary variable because of numerical imprecision
Normalization (2/2)
Correlations
Definition at line 1059 of file LayerCostModule.cc.
References PLearn::TMat< T >::clear(), PLearn::TVec< T >::clear(), PLearn::correlations(), PLearn::OnlineLearningModule::during_training, PLearn::fast_is_equal(), PLearn::TMat< T >::fill(), i, PLearn::OnlineLearningModule::input_size, inputs_cross_quadratic_mean_trainMemory, inputs_expectation_trainMemory, j, PLearn::TMat< T >::length(), momentum, one_count, PLearn::TMat< T >::resize(), PLearn::TVec< T >::resize(), and PLearn::sqrt().
{
int n_samples = inputs.length();
one_count = 1. / (real)n_samples;
Vec input;
expectation.resize( input_size );
expectation.clear();
cross_quadratic_mean.resize(input_size,input_size);
cross_quadratic_mean.clear();
stds.resize( input_size );
stds.clear();
correlations.resize(input_size,input_size);
correlations.fill(1.); // The default correlation is 1
for (int isample = 0; isample < n_samples; isample++)
{
input = inputs(isample);
for (int i = 0; i < input_size; i++)
{
expectation[i] += input[i];
cross_quadratic_mean(i,i) += input[i] * input[i];
for (int j = 0; j < i; j++)
cross_quadratic_mean(i,j) += input[i] * input[j];
}
}
for (int i = 0; i < input_size; i++)
{
expectation[i] *= one_count;
cross_quadratic_mean(i,i) *= one_count;
if( fast_is_equal(momentum, 0.)
|| !during_training )
{
real tmp = cross_quadratic_mean(i,i) - expectation[i] * expectation[i];
if( tmp > 0. ) // std[i] = 0 by default
stds[i] = sqrt( tmp );
}
for (int j = 0; j < i; j++)
{
cross_quadratic_mean(i,j) *= one_count;
if( fast_is_equal(momentum, 0.)
|| !during_training )
{
real tmp = stds[i] * stds[j];
if( !fast_is_equal(tmp, 0.) ) // correlations(i,j) = 1 by default
correlations(i,j) = ( cross_quadratic_mean(i,j)
- expectation[i]*expectation[j] ) / tmp;
}
}
}
if( !fast_is_equal(momentum, 0.) && during_training )
{
for (int i = 0; i < input_size; i++)
{
expectation[i] = momentum*inputs_expectation_trainMemory[i]
+(1.0-momentum)*expectation[i];
inputs_expectation_trainMemory[i] = expectation[i];
cross_quadratic_mean(i,i) = momentum*inputs_cross_quadratic_mean_trainMemory(i,i)
+(1.0-momentum)*cross_quadratic_mean(i,i);
inputs_cross_quadratic_mean_trainMemory(i,i) = cross_quadratic_mean(i,i);
real tmp = cross_quadratic_mean(i,i) - expectation[i] * expectation[i];
if( tmp > 0. ) // std[i] = 0 by default
stds[i] = sqrt( tmp );
for (int j = 0; j < i; j++)
{
cross_quadratic_mean(i,j) = momentum*inputs_cross_quadratic_mean_trainMemory(i,j)
+(1.0-momentum)*cross_quadratic_mean(i,j);
inputs_cross_quadratic_mean_trainMemory(i,j) = cross_quadratic_mean(i,j);
tmp = stds[i] * stds[j];
if( !fast_is_equal(tmp, 0.) ) // correlations(i,j) = 1 by default
correlations(i,j) = ( cross_quadratic_mean(i,j)
- expectation[i]*expectation[j] ) / tmp;
}
}
}
}
Definition at line 1503 of file LayerCostModule.cc.
References PLearn::TMat< T >::clear(), histo_index(), histo_size, i, PLearn::OnlineLearningModule::input_size, PLearn::TMat< T >::length(), one_count, PLASSERT, and PLearn::TMat< T >::resize().
{
int n_samples = inputs.length();
one_count = 1. / (real)n_samples;
histo.resize(input_size,histo_size);
histo.clear();
for (int isample = 0; isample < n_samples; isample++)
{
Vec input = inputs(isample);
for (int i = 0; i < input_size; i++)
{
PLASSERT( histo_index(input[i]) < histo_size);
histo( i, histo_index(input[i]) ) += one_count;
}
}
}
| void PLearn::LayerCostModule::computeHisto | ( | const Mat & | inputs | ) | [virtual] |
Some auxiliary function to deal with empirical histograms.
Definition at line 1498 of file LayerCostModule.cc.
References inputs_histo.
Referenced by bpropUpdate(), and fprop().
{
computeHisto(inputs,
inputs_histo);
}

Definition at line 1221 of file LayerCostModule.cc.
References cache_differ_count_i, cache_differ_count_j, cache_n_differ, PLearn::TVec< T >::clear(), PLearn::fast_exact_is_equal(), PLearn::TVec< T >::fill(), histo_size, HISTO_STEP, i, PLearn::OnlineLearningModule::input_size, inputs_histo, j, KLdivTerm(), and norm_factor.
Referenced by bpropUpdate(), and fprop().
{
if( store_in_cache )
{
real cost = 0.;
for (int i = 0; i < input_size; i++)
for (int j = 0; j < i; j++)
{
// These variables are used in case one bin of
// the histogram is empty for one unit
// and not for another one ( (Nj-Ni).log(Ni/Nj) = nan ).
// In such case, we ''differ'' the count for the next bin and so on.
cache_differ_count_i[ i ][ j ].clear();
cache_differ_count_j[ i ][ j ].clear();
cache_n_differ[i][j].fill( 0. );
// real last_positive_Ni_k, last_positive_Nj_k;
// real last_n_differ;
for (int k = 0; k < histo_size; k++)
{
real Ni_k = inputs_histo(i,k) + cache_differ_count_i[i][j][ k ];
real Nj_k = inputs_histo(j,k) + cache_differ_count_j[i][j][ k ];
if( fast_exact_is_equal(Ni_k, 0.0) )
{
if( k < histo_size - 1 ) // "cas ou on regroupe avec le dernier";
{
cache_differ_count_j[i][j][ k+1 ] = Nj_k;
cache_n_differ[i][j][ k+1 ] = cache_n_differ[i][j][ k ] + 1;
}
}
else if( fast_exact_is_equal(Nj_k, 0.0) )
{
if( k < histo_size - 1 ) // "cas ou on regroupe avec le dernier";
{
cache_differ_count_i[i][j][ k+1 ] = Ni_k;
cache_n_differ[i][j][ k+1 ] = cache_n_differ[i][j][ k ] + 1;
}
}
else
{
cost += KLdivTerm( Ni_k, Nj_k ) *(real)(1 + cache_n_differ[i][j][ k ]) *HISTO_STEP;
// last_positive_Ni_k = Ni_k;
// last_positive_Nj_k = Nj_k;
// last_n_differ = cache_n_differ[i][j][ k ];
}
// if( cache_differ_count_i[i][j][ histo_size - 1 ] > 0.0 )
// "cas ou on regroupe avec le dernier";
// else if ( cache_differ_count_j[i][j][ histo_size - 1 ] > 0.0 )
// "cas ou on regroupe avec le dernier";
}
}
// Normalization w.r.t. number of units
return cost *norm_factor;
}
else
return computeKLdiv(inputs_histo);
}

Definition at line 1157 of file LayerCostModule.cc.
References PLearn::fast_exact_is_equal(), histo_size, HISTO_STEP, i, PLearn::OnlineLearningModule::input_size, j, KLdivTerm(), PLearn::TMat< T >::length(), norm_factor, PLASSERT, and PLearn::TMat< T >::width().
{
PLASSERT( histo.length() == input_size );
PLASSERT( histo.width() == histo_size );
real cost = 0.;
for (int i = 0; i < input_size; i++)
for (int j = 0; j < i; j++)
{
// These variables are used in case one bin of
// the histogram is empty for one unit
// and not for another one ( (Nj-Ni).log(Ni/Nj) = nan ).
// In such case, we ''differ'' the count for the next bin and so on.
real differ_count_i = 0.;
real differ_count_j = 0.;
int n_differ = 0;
// real last_positive_Ni_k, last_positive_Nj_k;
// int last_n_differ;
for (int k = 0; k < histo_size; k++)
{
real Ni_k = histo( i, k ) + differ_count_i;
real Nj_k = histo( j, k ) + differ_count_j;
if( fast_exact_is_equal(Ni_k, 0.0) )
{
differ_count_j = Nj_k;
n_differ += 1;
}
else if( fast_exact_is_equal(Nj_k, 0.0) )
{
differ_count_i = Ni_k;
n_differ += 1;
}
else
{
cost += KLdivTerm( Ni_k, Nj_k ) *(real)(1+n_differ) *HISTO_STEP;
differ_count_i = 0.0;
differ_count_j = 0.0;
n_differ = 0;
// last_positive_Ni_k = Ni_k;
// last_positive_Nj_k = Nj_k;
// last_n_differ = n_differ;
}
}
// if( differ_count_i > 0.0 )
// {
// "cas ou on regroupe avec le dernier";
// cost -= KLdivTerm(last_positive_Ni_k,last_positive_Nj_k)
// *(real)(1+last_n_differ) *HISTO_STEP;
// cost += KLdivTerm(last_positive_Ni_k+differ_count_i,last_positive_Nj_k)
// *(real)(1+last_n_differ+n_differ) *HISTO_STEP;
// }
//
// else if ( differ_count_j > 0.0 )
// {
// "cas ou on regroupe avec le dernier";
// cost -= KLdivTerm(last_positive_Ni_k,last_positive_Nj_k)
// *(real)(1+last_n_differ) *HISTO_STEP;
// cost += KLdivTerm(last_positive_Ni_k,last_positive_Nj_k+differ_count_j)
// *(real)(1+last_n_differ+n_differ) *HISTO_STEP;
// }
}
// Normalization w.r.t. number of units
return cost *norm_factor;
}
| void PLearn::LayerCostModule::computePascalStatistics | ( | const Mat & | inputs | ) | [virtual] |
Auxiliary function for the pascal's cost function.
Definition at line 953 of file LayerCostModule.cc.
References inputs_cross_quadratic_mean, and inputs_expectation.
Referenced by bpropUpdate(), and fprop().
{
computePascalStatistics( inputs,
inputs_expectation, inputs_cross_quadratic_mean);
}

| void PLearn::LayerCostModule::computePascalStatistics | ( | const Mat & | inputs, |
| Vec & | expectation, | ||
| Mat & | cross_quadratic_mean | ||
| ) | const [virtual] |
Definition at line 959 of file LayerCostModule.cc.
References PLearn::TMat< T >::clear(), PLearn::TVec< T >::clear(), PLearn::OnlineLearningModule::during_training, i, PLearn::OnlineLearningModule::input_size, inputs_cross_quadratic_mean, inputs_cross_quadratic_mean_trainMemory, inputs_expectation, inputs_expectation_trainMemory, j, PLearn::TMat< T >::length(), momentum, one_count, PLearn::TMat< T >::resize(), and PLearn::TVec< T >::resize().
{
int n_samples = inputs.length();
one_count = 1. / (real)n_samples;
Vec input;
expectation.resize( input_size );
expectation.clear();
cross_quadratic_mean.resize(input_size,input_size);
cross_quadratic_mean.clear();
inputs_expectation.clear();
inputs_cross_quadratic_mean.clear();
for (int isample = 0; isample < n_samples; isample++)
{
input = inputs(isample);
for (int i = 0; i < input_size; i++)
{
expectation[i] += input[i];
for (int j = 0; j < i; j++)
cross_quadratic_mean(i,j) += input[i] * input[j];
}
}
for (int i = 0; i < input_size; i++)
{
expectation[i] *= one_count;
for (int j = 0; j < i; j++)
cross_quadratic_mean(i,j) *= one_count;
}
if( ( momentum > 0.0 ) && during_training )
{
for (int i = 0; i < input_size; i++)
{
expectation[i] = momentum*inputs_expectation_trainMemory[i]
+(1.0-momentum)*expectation[i];
inputs_expectation_trainMemory[i] = expectation[i];
for (int j = 0; j < i; j++)
{
cross_quadratic_mean(i,j) = momentum*inputs_cross_quadratic_mean_trainMemory(i,j)
+(1.0-momentum)*cross_quadratic_mean(i,j);
inputs_cross_quadratic_mean_trainMemory(i,j) = cross_quadratic_mean(i,j);
}
}
}
}
| void PLearn::LayerCostModule::computeSafeHisto | ( | const Mat & | inputs | ) | [virtual] |
Auxiliary functions for kl_div_simple cost function.
Definition at line 1523 of file LayerCostModule.cc.
References inputs_histo.
Referenced by bpropUpdate(), and fprop().
{
computeSafeHisto(inputs,
inputs_histo);
}

Definition at line 1528 of file LayerCostModule.cc.
References PLearn::TMat< T >::fill(), histo_index(), histo_size, i, PLearn::OnlineLearningModule::input_size, PLearn::TMat< T >::length(), one_count, and PLearn::TMat< T >::resize().
{
int n_samples = inputs.length();
one_count = 1. / (real)(n_samples+histo_size);
histo.resize(input_size,histo_size);
histo.fill(one_count);
for (int isample = 0; isample < n_samples; isample++)
{
Vec input = inputs(isample);
for (int i = 0; i < input_size; i++)
histo(i, histo_index(input[i])) += one_count;
}
}
| TVec< string > PLearn::LayerCostModule::costNames | ( | ) | [virtual] |
Indicates the name of the computed costs.
Reimplemented from PLearn::CostModule.
Definition at line 1586 of file LayerCostModule.cc.
References PLearn::OnlineLearningModule::name.
{
return TVec<string>(1, name);
}
| void PLearn::LayerCostModule::declareOptions | ( | OptionList & | ol | ) | [static, protected] |
Declares the class options.
Reimplemented from PLearn::CostModule.
Definition at line 73 of file LayerCostModule.cc.
References alpha, PLearn::OptionBase::buildoption, cost_function, cost_function_completename, PLearn::declareOption(), PLearn::CostModule::declareOptions(), histo_size, inputs_cross_quadratic_mean_trainMemory, inputs_expectation_trainMemory, PLearn::OptionBase::learntoption, momentum, PLearn::OptionBase::nosave, nstages_max, optimization_strategy, penalty_function, and stage.
{
// Now call the parent class' declareOptions
inherited::declareOptions(ol);
declareOption(ol, "cost_function", &LayerCostModule::cost_function,
OptionBase::buildoption,
"The cost function applied to the layer:\n"
"- \"pascal\" :"
" Pascal Vincent's God given cost function.\n"
"- \"correlation\":"
" average of a function applied to the correlations between outputs.\n"
"- \"kl_div\":"
" KL divergence between distrubution of outputs (sampled with x)\n"
"- \"kl_div_simple\":"
" simple version of kl_div where we count at least one sample per histogram's bin\n"
"- \"stochastic_cross_entropy\" [default]:"
" average cross-entropy between pairs of binomial units\n"
"- \"stochastic_kl_div\":"
" average KL divergence between pairs of binomial units\n"
);
declareOption(ol, "nstages_max", &LayerCostModule::nstages_max,
OptionBase::buildoption,
"Maximal number of updates for which the gradient of the cost function will be propagated.\n"
"-1 means: always train without limit.\n"
);
declareOption(ol, "optimization_strategy", &LayerCostModule::optimization_strategy,
OptionBase::buildoption,
"Strategy to compute the gradient:\n"
"- \"standard\": standard computation\n"
"- \"half\": we will propagate the gradient only on units tagged as i < j.\n"
"- \"random_half\": idem than 'half' with the order of the indices that changes randomly during training.\n"
);
declareOption(ol, "momentum", &LayerCostModule::momentum,
OptionBase::buildoption,
"(in [0,1[) For non stochastic cost functions, momentum to compute the moving means.\n"
);
declareOption(ol, "histo_size", &LayerCostModule::histo_size,
OptionBase::buildoption,
"For \"kl_div\" cost functions,\n"
"number of bins for the histograms (to estimate distributions of outputs).\n"
"The higher is histo_size, the more precise is the estimation.\n"
);
declareOption(ol, "alpha", &LayerCostModule::alpha,
OptionBase::buildoption,
"(>=0) For \"pascal\" cost function,\n"
"number of bins for the histograms (to estimate distributions of outputs).\n"
"The higher is histo_size, the more precise is the estimation.\n"
);
declareOption(ol, "penalty_function", &LayerCostModule::penalty_function,
OptionBase::buildoption,
"(For non-stochastic cost functions)\n"
"Function applied to the local cost between two inputs to compute\n"
"the global cost on the whole set of inputs (by averaging).\n"
"- \"square\": f(x)= x^2 \n"
"- \"log\": f(x)= -log( 1 - x) \n"
"- \"exp\": f(x)= exp( x ) \n"
"- \"linear\": f(x)= x \n"
);
declareOption(ol, "cost_function_completename", &LayerCostModule::cost_function_completename,
OptionBase::learntoption,
"complete name of cost_function (take into account some internal settings).\n"
);
declareOption(ol, "stage", &LayerCostModule::stage,
OptionBase::learntoption,
"number of stages that has been done during the training.\n"
);
declareOption(ol, "inputs_expectation_trainMemory", &LayerCostModule::inputs_expectation_trainMemory,
OptionBase::nosave,
"Correlation of the outputs, for all pairs of units.\n"
);
declareOption(ol, "inputs_cross_quadratic_mean_trainMemory", &LayerCostModule::inputs_cross_quadratic_mean_trainMemory,
OptionBase::nosave,
"Expectation of the cross products between outputs, for all pairs of units.\n"
);
}

| static const PPath& PLearn::LayerCostModule::declaringFile | ( | ) | [inline, static] |
| LayerCostModule * PLearn::LayerCostModule::deepCopy | ( | CopiesMap & | copies | ) | const [virtual] |
Reimplemented from PLearn::CostModule.
Definition at line 54 of file LayerCostModule.cc.
: some are valid only for binomial layers. \n");
Definition at line 1280 of file LayerCostModule.cc.
References cache_differ_count_i, cache_differ_count_j, cache_n_differ, PLearn::fast_exact_is_equal(), histo_size, HISTO_STEP, i, inputs_histo, j, KLdivTerm(), norm_factor, one_count, and PLASSERT.
Referenced by bpropUpdate().
{
PLASSERT( index_i < histo_size - 1 );
// already tested in the code of BackPropAccUpdate()
PLASSERT( over_dq > 0. );
PLASSERT( inputs_histo( i, index_i ) > 0. );
// Verifies that:
// ( inputs_histo is up to date
// => ) the input(isample,i) has been counted
real grad_update = 0.0;
real Ni_ki, Nj_ki, Ni_ki_shift1, Nj_ki_shift1;
real n_differ_before_ki, n_differ_before_ki_shift1;
if( i > j ) // Because cache memory matrix are symmetric but not completely filled
{
Ni_ki = inputs_histo( i, index_i ) + cache_differ_count_i[ i ][ j ][ index_i ];
Nj_ki = inputs_histo( j, index_i ) + cache_differ_count_j[ i ][ j ][ index_i ];
Ni_ki_shift1 = inputs_histo( i, index_i + 1 ) + cache_differ_count_i[ i ][ j ][ index_i + 1 ];
Nj_ki_shift1 = inputs_histo( j, index_i + 1 ) + cache_differ_count_j[ i ][ j ][ index_i + 1 ];
n_differ_before_ki = cache_n_differ[ i ][ j ][ index_i ];
n_differ_before_ki_shift1 = cache_n_differ[ i ][ j ][ index_i + 1 ];
}
else // ( i < j ) // Be very careful with indices here!
{
Ni_ki = inputs_histo( i, index_i ) + cache_differ_count_j[ j ][ i ][ index_i ];
Nj_ki = inputs_histo( j, index_i ) + cache_differ_count_i[ j ][ i ][ index_i ];
Ni_ki_shift1 = inputs_histo( i, index_i + 1 ) + cache_differ_count_j[ j ][ i ][ index_i + 1 ];
Nj_ki_shift1 = inputs_histo( j, index_i + 1 ) + cache_differ_count_i[ j ][ i ][ index_i + 1 ];
n_differ_before_ki = cache_n_differ[ j ][ i ][ index_i ];
n_differ_before_ki_shift1 = cache_n_differ[ j ][ i ][ index_i + 1 ];
}
real additional_differ_count_j_after = 0.;
real n_differ_after_ki = n_differ_before_ki;
real n_differ_after_ki_shift1 = n_differ_before_ki_shift1;
// What follows is only valuable when the qi's are increased (dq>0).
if( !fast_exact_is_equal(Nj_ki, 0.0) )
// if it is zero, then INCREASING qi will not change anything
// (it was already counted in the next histograms's bin
{
// removing the term of the sum that will be modified
grad_update -= KLdivTerm( Ni_ki,
Nj_ki )
* ( 1 + n_differ_before_ki);
if( fast_exact_is_equal(Ni_ki, one_count) )
{
additional_differ_count_j_after = Nj_ki;
n_differ_after_ki_shift1 = n_differ_after_ki + 1;
// = n_differ_before_ki + 1;
}
else
{
// adding the term of the sum with its modified value
grad_update += KLdivTerm( Ni_ki - one_count,
Nj_ki )
* ( 1 + n_differ_after_ki );
}
if( !fast_exact_is_equal(Nj_ki_shift1,0.0) )
{
// adding the term of the sum with its modified value
grad_update += KLdivTerm( Ni_ki_shift1 + one_count,
Nj_ki_shift1 + additional_differ_count_j_after )
* ( 1 + n_differ_after_ki_shift1 );
if( !fast_exact_is_equal(Ni_ki_shift1, 0.0) ) // "cas ou on regroupe avec le dernier";
{
// removing the term of the sum that will be modified
grad_update -= KLdivTerm( Ni_ki_shift1,
Nj_ki_shift1 )
* ( 1 + n_differ_before_ki_shift1 );
}
else // ( Ni_ki_shift1 == 0.0 )
{
// We search ki' > k(i)+1 such that n(i,ki') > 0
real additional_differ_count_j_before = 0.;
real additional_n_differ_before_ki_shift1 = 0.;
int ki;
for (ki = index_i+2; ki < histo_size; ki++)
{
additional_differ_count_j_before += inputs_histo( j, ki );
additional_n_differ_before_ki_shift1 += 1;
if( inputs_histo( i, ki )>0 )
break;
}
if( ki < histo_size )
{
grad_update -= KLdivTerm( inputs_histo( i, ki ),
Nj_ki_shift1 + additional_differ_count_j_before )
* ( 1 + n_differ_before_ki_shift1 + additional_n_differ_before_ki_shift1 );
if( additional_differ_count_j_before > 0. )
// We have to report the additional count for unit j
{
grad_update += KLdivTerm( inputs_histo( i, ki ),
additional_differ_count_j_before )
* ( additional_n_differ_before_ki_shift1 );
}
}
}
}
else // ( Nj_ki_shift1 == 0.0 )
{
real additional_differ_count_i_before = 0.;
// We search kj > ki+1 tq inputs_histo( j, kj ) > 0.
int kj;
for( kj = index_i+2; kj < histo_size; kj++)
{
additional_differ_count_i_before += inputs_histo( i, kj );
n_differ_before_ki_shift1 += 1;
if( inputs_histo( j, kj ) > 0. )
break;
}
if ( !fast_exact_is_equal(additional_differ_count_j_after, 0. ) )
n_differ_after_ki_shift1 = n_differ_before_ki_shift1;
if( kj < histo_size )
{
if ( fast_exact_is_equal(n_differ_after_ki_shift1, n_differ_before_ki_shift1) )
{
// ( no qj were differed after we changed count at bin ki )
// OR ( some qj were differed to bin ki+1 AND the bin were not empty )
grad_update += KLdivTerm( Ni_ki_shift1 + additional_differ_count_i_before + one_count,
inputs_histo( j, kj ) + additional_differ_count_j_after )
* ( 1 + n_differ_after_ki_shift1 );
}
else
{
PLASSERT( n_differ_before_ki_shift1 > n_differ_after_ki_shift1 );
grad_update += KLdivTerm( Ni_ki_shift1 + one_count,
additional_differ_count_j_after )
* ( 1 + n_differ_after_ki_shift1 );
grad_update += KLdivTerm( additional_differ_count_i_before,
inputs_histo( j, kj ) )
* ( n_differ_before_ki_shift1 - n_differ_after_ki_shift1 );
}
if( !fast_exact_is_equal(Ni_ki_shift1 + additional_differ_count_i_before,0.0) )
{
grad_update -= KLdivTerm( Ni_ki_shift1 + additional_differ_count_i_before,
inputs_histo( j, kj ) )
* ( 1 + n_differ_before_ki_shift1 );
}
else // ( Ni_ki_shift1' == 0 == Nj_ki_shift1 ) && ( pas de q[i] avant q[j']... )
{
// We search ki' > kj+1 tq inputs_histo( i, ki' ) > 0.
real additional_differ_count_j_before = 0.;
real additional_n_differ_before_ki_shift1 = 0.;
int kj2;
for( kj2 = kj+1; kj2 < histo_size; kj2++)
{
additional_differ_count_j_before += inputs_histo( j, kj2 );
additional_n_differ_before_ki_shift1 += 1;
if( inputs_histo( i, kj2 ) > 0. )
break;
}
if ( fast_exact_is_equal(additional_differ_count_j_before, 0. ) )
n_differ_after_ki_shift1 = n_differ_before_ki_shift1;
if( kj2 < histo_size )
{
grad_update -= KLdivTerm( inputs_histo( i, kj2 ),
Nj_ki_shift1 + additional_differ_count_j_before )
* ( 1 + n_differ_before_ki_shift1 + additional_n_differ_before_ki_shift1 );
if( additional_differ_count_j_before > 0. )
{
grad_update += KLdivTerm( inputs_histo( i, kj2 ),
additional_differ_count_j_before )
* ( additional_n_differ_before_ki_shift1 );
}
}
}
}
}
}
return grad_update *HISTO_STEP *over_dq *norm_factor;
}


| real PLearn::LayerCostModule::delta_SafeKLdivTerm | ( | int | i, |
| int | j, | ||
| int | index_i, | ||
| real | over_dq | ||
| ) | [virtual] |
Definition at line 1461 of file LayerCostModule.cc.
References PLearn::fast_exact_is_equal(), histo_size, inputs_histo, KLdivTerm(), one_count, and PLASSERT.
Referenced by bpropUpdate().
{
//PLASSERT( over_dq > 0.0 )
PLASSERT( index_i < histo_size - 1 );
real grad_update = 0.0;
real Ni_ki = inputs_histo(i,index_i);
PLASSERT( !fast_exact_is_equal(Ni_ki, 0.0) ); // Verification:
// if inputs_histo is up to date,
// the input(isample,i) has been counted
real Ni_ki_shift1 = inputs_histo(i,index_i+1);
real Nj_ki = inputs_histo(j,index_i);
real Nj_ki_shift1 = inputs_histo(j,index_i+1);
// removing the term of the sum that will be modified
grad_update -= KLdivTerm( Ni_ki, Nj_ki );
// adding the term of the sum with its modified value
grad_update += KLdivTerm( Ni_ki-one_count, Nj_ki );
grad_update += KLdivTerm( Ni_ki_shift1+one_count, Nj_ki_shift1 );
grad_update -= KLdivTerm( Ni_ki_shift1, Nj_ki_shift1 );
return grad_update *over_dq;
}


Definition at line 1027 of file LayerCostModule.cc.
References PLearn::exp(), EXP_FUNC, PLearn::fast_is_equal(), LINEAR_FUNC, LOG_FUNC, PLERROR, POW4_FUNC, and SQUARE_FUNC.
Referenced by bpropUpdate().
{
if( SQUARE_FUNC )
return 2. * value;
if( POW4_FUNC )
return 4. * value * value * value;
if( LOG_FUNC )
{
if( fast_is_equal( value, 1. ) )
return REAL_MAX;
return 1. / (1. - value);
}
if( EXP_FUNC )
return exp(value);
if( LINEAR_FUNC )
return 1.;
PLERROR("in LayerCostModule::deriv_func_() no boolean *_FUNC has been set.");
return REAL_MAX;
}

Definition at line 1568 of file LayerCostModule.cc.
References HISTO_STEP.
Referenced by bpropUpdate().
{
// ** Simple version **
return HISTO_STEP;
// ** Elaborated version **
//if( fast_exact_is_equal( round(q*(real)histo_size) , ceil(q*(real)histo_size) ) )
// return HISTO_STEP;
//else
// return -HISTO_STEP;
// ** BAD VERSION: too unstable **
// return (real)histo_index(q+1.0/(real)histo_size)/(real)histo_size - q;
}

| void PLearn::LayerCostModule::forget | ( | ) | [virtual] |
reset the parameters to the state they would be BEFORE starting training.
Note that this method is necessarily called from build().
Reimplemented from PLearn::CostModule.
Definition at line 276 of file LayerCostModule.cc.
References average_deriv, PLearn::TVec< T >::clear(), PLearn::TMat< T >::clear(), inputs_correlations, inputs_cross_quadratic_mean, inputs_cross_quadratic_mean_trainMemory, inputs_expectation, inputs_expectation_trainMemory, inputs_histo, inputs_stds, momentum, one_count, and stage.
{
inputs_histo.clear();
inputs_expectation.clear();
inputs_stds.clear();
inputs_correlations.clear();
inputs_cross_quadratic_mean.clear();
if( momentum > 0.0)
{
inputs_expectation_trainMemory.clear();
inputs_cross_quadratic_mean_trainMemory.clear();
}
one_count = 0.;
stage = 0;
average_deriv = 0.;
}
given the input and target, compute the cost
************************************************************ average *** CROSS ENTROPY *** between pairs of units (given output = sigmoid(act) )
cost = - MEAN_{i,j::i} CrossEntropy[( P(h_{i}|x) | P(h_{j}|x) )]
= - MEAN_{i,j::i} [ q{i}.log(q{j}) + (1-q{i}).log(1-q{j}) ]
where | h_{i}: i^th units of the layer \ P(.|x): output for input data x \ q{i}=P(h{i}=1|v): output of the i^th units of the layer
************************************************************ average SYMETRIC *** K-L DIVERGENCE *** between pairs of units (given outputs = sigmoid(act) )
cost = - MEAN_{i,j::i} Div_{KL} [( P(h_{i}|v) | P(h_{j}|v) )]
= - MEAN_{i,j::i} [ ( q{j} - q{i} ) log( q{i}/(1-q{i})*(1-q{j})/q{j} ) ]
where | h_{i}: i^th units of the layer \ P(.|v): output for input data x \ q{i}=P(h{i}=1|v): output of the i^th units of the layer
Definition at line 482 of file LayerCostModule.cc.
References cost_function, PLearn::fast_exact_is_equal(), i, PLearn::OnlineLearningModule::input_size, is_cost_function_stochastic, j, norm_factor, PLASSERT, PLERROR, PLearn::safeflog(), and PLearn::TVec< T >::size().
Referenced by fprop().
{
PLASSERT( input.size() == input_size );
PLASSERT( is_cost_function_stochastic );
cost = 0.0;
real qi, qj, comp_qi, comp_qj; // The outputs (units i,j)
// and some basic operations on it (e.g.: 1-qi, qi/(1-qi))
if( cost_function == "stochastic_cross_entropy" )
{
for( int i = 0; i < input_size; i++ )
{
qi = input[i];
comp_qi = 1.0 - qi;
for( int j = 0; j < i; j++ )
{
qj = input[j];
comp_qj = 1.0 - qj;
// H(pi||pj) = H(pi) + D_{KL}(pi||pj)
cost += qi*safeflog(qj) + comp_qi*safeflog(comp_qj);
// The symetric part (loop j=i+1...size)
cost += qj*safeflog(qi) + comp_qj*safeflog(comp_qi);
}
}
// Normalization w.r.t. number of units
cost *= norm_factor;
}
else if( cost_function == "stochastic_kl_div" )
{
for( int i = 0; i < input_size; i++ )
{
qi = input[i];
if(fast_exact_is_equal(qi, 1.0))
comp_qi = REAL_MAX;
else
comp_qi = qi/(1.0 - qi);
for( int j = 0; j < i; j++ )
{
qj = input[j];
if(fast_exact_is_equal(qj, 1.0))
comp_qj = REAL_MAX;
else
comp_qj = qj/(1.0 - qj);
// - D_{KL}(pi||pj) - D_{KL}(pj||pi)
cost += (qj-qi)*safeflog(comp_qi/comp_qj);
}
}
// Normalization w.r.t. number of units
cost *= norm_factor;
}
else
PLERROR("LayerCostModule::fprop() not implemented for cost_cfunction '%s'\n"
"- It may be a printing error.\n"
"- You can try to call LayerCostModule::fprop(const Mat& inputs, Mat& costs)"
" if your cost function is non stochastic.\n"
"- Or else write the code corresponding to your cost function.\n",
cost_function.c_str());
}
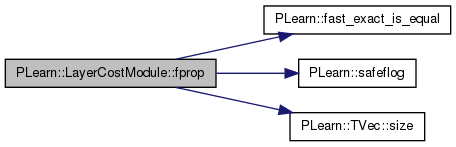

Overridden to try to use the standard mini-batch fprop when possible.
Reimplemented from PLearn::CostModule.
Definition at line 323 of file LayerCostModule.cc.
References fprop(), getPortIndex(), PLearn::TMat< T >::isEmpty(), PLearn::TVec< T >::length(), PLearn::OnlineLearningModule::nPorts(), and PLASSERT.
{
Mat* p_inputs = ports_value[getPortIndex("input")];
Mat* p_costs = ports_value[getPortIndex("cost")];
PLASSERT( ports_value.length() == nPorts() );
if ( p_costs && p_costs->isEmpty() )
{
PLASSERT( p_inputs && !p_inputs->isEmpty() );
//cout << "fprop" << endl;
fprop(*p_inputs, *p_costs);
}
}
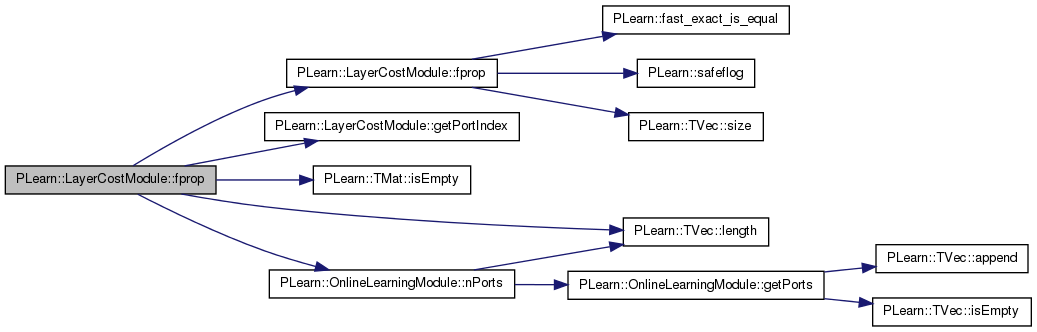
************************************************************ (non stochastic) SYMETRIC *** K-L DIVERGENCE *** between probabilities of outputs vectors for all units
cost = - MEAN_{i,j::i} Div_{KL}[ Px(q{i}) | Px(q{j}) ]
= - MEAN_{i,j::i} SUM_Q (Nx_j(Q) - Nx_j(Q)) log( Nx_i(Q) / Nx_j(Q) )
where q{i} = P(h{i}=1|x): output of the i^th units of the layer. Px(.): empirical probability (given data x, we sample the q's). Q: interval in [0,1] = one bin of the histogram of the outputs q's. Q has size HISTO_STEP Nx_i(Q): proportion of q{i} that belong to Q, given data x.
Note1: one q{i} *entirely* determines one binomial densities of probability. ( Bijection {binomial Proba functions} <-> |R )
Note2: there is a special processing for cases when NO outputs q{i} were observed for a given unit i at a given bin Q of the histograms whereas another q{j} has been observed in Q (normally, KLdiv -> infinity ). SEE function computeKLdiv().
************************************************************ same as above with a very simple version of the KL-div: when computing the histogram of the outputs for all units. we add one count per histogram's bin so as to avoid numerical problems with zeros.
SEE function computeSafeHisto(real ).
************************************************************ a Pascal Vincent's god-given similarity measure between outputs vectors for all units
cost = MEAN_{i,j::i} f( Ex[q{i}.q{j}] ) - alpha. MEAN_{i} f( Ex[q{i}] )
where q{i} = P(h{i}=1|x): output of the i^th units of the layer Ex(.): empirical expectation (given data x)
************************************************************ a correlation measure between outputs for all units
( Ex[q{i}.q{j}] - Ex[q{i}]Ex[q{j}] ) cost = MEAN_{i,j::i} f( -------------------------------- ) ( StDx(q{i}) * StDx(q{j}) )
where q{i} = P(h{i}=1|x): output of the i^th units of the layer Ex(.): empirical esperance (given data x) StDx(.): empirical standard deviation (given data x)
Definition at line 344 of file LayerCostModule.cc.
References alpha, PLearn::TMat< T >::clear(), computeCorrelationStatistics(), computeHisto(), computeKLdiv(), computePascalStatistics(), computeSafeHisto(), PLearn::correlations(), cost_function, PLearn::OnlineLearningModule::during_training, PLearn::TMat< T >::fill(), fprop(), func_(), histo_size, i, PLearn::OnlineLearningModule::input_size, is_cost_function_stochastic, j, KLdivTerm(), PLearn::TMat< T >::length(), MISSING_VALUE, norm_factor, PLearn::OnlineLearningModule::output_size, PLASSERT, PLearn::TMat< T >::resize(), and PLearn::TMat< T >::width().
{
PLASSERT( input_size > 1 );
int n_samples = inputs.length();
costs.resize( n_samples, output_size );
// The fprop will be done during training (only needed computations)
if( during_training )
{
costs.fill( MISSING_VALUE );
return;
}
else
costs.clear();
if( !is_cost_function_stochastic )
{
PLASSERT( inputs.width() == input_size );
if( cost_function == "kl_div" )
{
Mat histo;
computeHisto( inputs, histo );
costs(0,0) = computeKLdiv( histo );
}
else if( cost_function == "kl_div_simple" )
{
Mat histo;
computeSafeHisto( inputs, histo );
// Computing the KL divergence
for (int i = 0; i < input_size; i++)
for (int j = 0; j < i; j++)
for (int k = 0; k < histo_size; k++)
costs(0,0) += KLdivTerm( histo(i,k), histo(j,k));
// Normalization w.r.t. number of units
costs(0,0) *= norm_factor;
}
else if( cost_function == "pascal" )
{
Vec expectation;
Mat cross_quadratic_mean;
computePascalStatistics( inputs, expectation, cross_quadratic_mean );
// Computing the cost
for (int i = 0; i < input_size; i++)
{
if (alpha > 0.0 )
costs(0,0) -= alpha * func_( expectation[i] ) *(real)(input_size-1);
for (int j = 0; j < i; j++)
costs(0,0) += func_( cross_quadratic_mean(i,j) );
}
costs(0,0) *= norm_factor;
}
else if( cost_function == "correlation" )
{
Vec expectation;
Mat cross_quadratic_mean;
Vec stds;
Mat correlations;
computeCorrelationStatistics( inputs, expectation, cross_quadratic_mean, stds, correlations );
// Computing the cost
for (int i = 0; i < input_size; i++)
for (int j = 0; j < i; j++)
costs(0,0) += func_( correlations(i,j) );
costs(0,0) *= norm_factor;
}
}
else // stochastic cost function
for (int isample = 0; isample < n_samples; isample++)
fprop(inputs(isample), costs(isample,0));
}
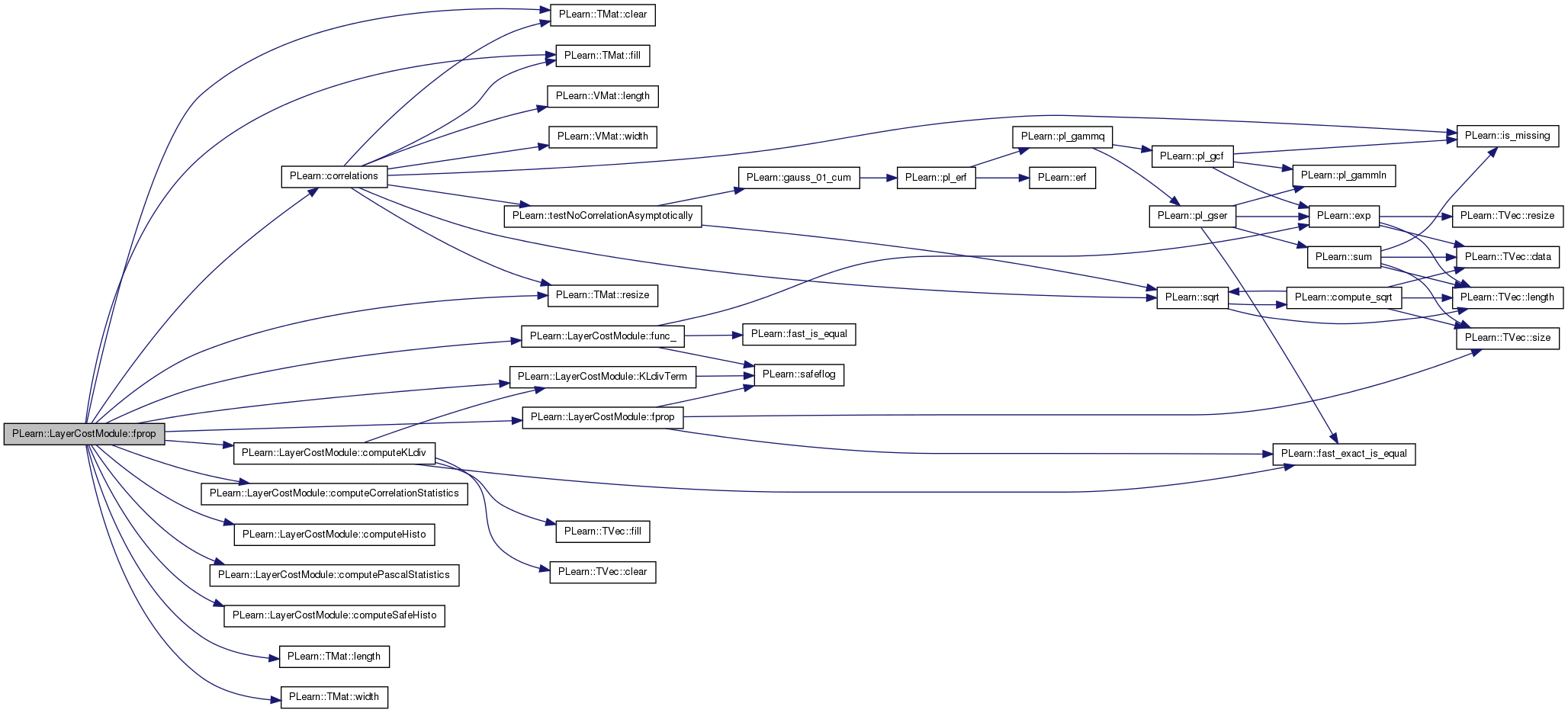
| void PLearn::LayerCostModule::fprop | ( | const Mat & | inputs, |
| const Mat & | targets, | ||
| Mat & | costs | ||
| ) | const [virtual] |
Mini-batch version with several costs..
Reimplemented from PLearn::CostModule.
Definition at line 339 of file LayerCostModule.cc.
References fprop().
{
fprop( inputs, costs );
}

Definition at line 1008 of file LayerCostModule.cc.
References PLearn::exp(), EXP_FUNC, PLearn::fast_is_equal(), LINEAR_FUNC, LOG_FUNC, PLERROR, POW4_FUNC, PLearn::safeflog(), and SQUARE_FUNC.
Referenced by fprop().
{
if( SQUARE_FUNC )
return value * value;
if( POW4_FUNC )
return value * value * value * value;
if( LOG_FUNC )
{
if( fast_is_equal( value, 1. ) || value > 1. )
return REAL_MAX;
return -safeflog( 1.-value );
}
if( EXP_FUNC )
return exp(value);
if( LINEAR_FUNC )
return value;
PLERROR("in LayerCostModule::func_() no boolean *_FUNC has been set.");
return REAL_MAX;
}
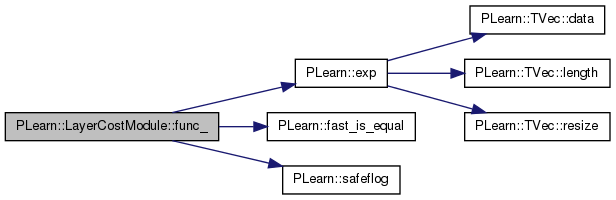

| OptionList & PLearn::LayerCostModule::getOptionList | ( | ) | const [virtual] |
Reimplemented from PLearn::CostModule.
Definition at line 54 of file LayerCostModule.cc.
: some are valid only for binomial layers. \n");
| OptionMap & PLearn::LayerCostModule::getOptionMap | ( | ) | const [virtual] |
Reimplemented from PLearn::CostModule.
Definition at line 54 of file LayerCostModule.cc.
: some are valid only for binomial layers. \n");
| int PLearn::LayerCostModule::getPortIndex | ( | const string & | port | ) | [virtual] |
Return the index (as in the list of ports returned by getPorts()) of a given port.
If 'port' does not exist, -1 is returned.
Reimplemented from PLearn::OnlineLearningModule.
Definition at line 1620 of file LayerCostModule.cc.
References portname_to_index.
Referenced by bpropAccUpdate(), build_(), and fprop().
{
map<string, int>::const_iterator it = portname_to_index.find(port);
if (it == portname_to_index.end())
return -1;
else
return it->second;
}

| const TVec< string > & PLearn::LayerCostModule::getPorts | ( | ) | [virtual] |
Returns all ports in a RBMModule.
Reimplemented from PLearn::CostModule.
Definition at line 1604 of file LayerCostModule.cc.
References ports.
{
return ports;
}
The ports' sizes are given by the corresponding RBM layers.
Reimplemented from PLearn::CostModule.
Definition at line 1612 of file LayerCostModule.cc.
References PLearn::OnlineLearningModule::port_sizes.
{
return port_sizes;
}
| RemoteMethodMap & PLearn::LayerCostModule::getRemoteMethodMap | ( | ) | const [virtual] |
Reimplemented from PLearn::CostModule.
Definition at line 54 of file LayerCostModule.cc.
: some are valid only for binomial layers. \n");
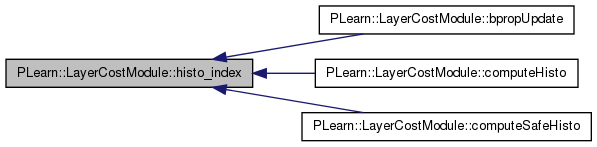
Definition at line 1548 of file LayerCostModule.cc.
References histo_size, and PLASSERT.
Referenced by bpropUpdate(), computeHisto(), and computeSafeHisto().
{
PLASSERT( (q >= 0.) && (q <= 1.) );
if( q >= 1. )
return histo_size - 1;
PLASSERT( (int)floor(q*(real)histo_size) < histo_size );
// LINEAR SCALE
return (int)floor(q*(real)histo_size);
}
Definition at line 1492 of file LayerCostModule.cc.
References PLearn::safeflog().
Referenced by computeKLdiv(), delta_KLdivTerm(), delta_SafeKLdivTerm(), and fprop().
{
return ( pj - pi ) * safeflog( pi/pj );
}


| void PLearn::LayerCostModule::makeDeepCopyFromShallowCopy | ( | CopiesMap & | copies | ) | [virtual] |
Transforms a shallow copy into a deep copy.
Reimplemented from PLearn::CostModule.
Definition at line 295 of file LayerCostModule.cc.
References cache_differ_count_i, cache_differ_count_j, cache_n_differ, PLearn::deepCopyField(), inputs_correlations, inputs_cross_quadratic_mean, inputs_cross_quadratic_mean_trainMemory, inputs_expectation, inputs_expectation_trainMemory, inputs_histo, inputs_stds, PLearn::CostModule::makeDeepCopyFromShallowCopy(), and ports.
{
inherited::makeDeepCopyFromShallowCopy(copies);
deepCopyField(inputs_histo, copies);
deepCopyField(inputs_expectation, copies);
deepCopyField(inputs_stds, copies);
deepCopyField(inputs_correlations, copies);
deepCopyField(inputs_cross_quadratic_mean, copies);
deepCopyField(inputs_expectation_trainMemory, copies);
deepCopyField(inputs_cross_quadratic_mean_trainMemory, copies);
deepCopyField(cache_differ_count_i, copies);
deepCopyField(cache_differ_count_j, copies);
deepCopyField(cache_n_differ, copies);
deepCopyField(ports, copies);
}

| virtual void PLearn::LayerCostModule::setLearningRate | ( | real | dynamic_learning_rate | ) | [inline, virtual] |
Overridden to do nothing (in particular, no warning).
Reimplemented from PLearn::OnlineLearningModule.
Definition at line 162 of file LayerCostModule.h.
{}
Reimplemented from PLearn::CostModule.
Definition at line 172 of file LayerCostModule.h.
Parameter in pascal's cost function.
Definition at line 71 of file LayerCostModule.h.
Referenced by bpropUpdate(), declareOptions(), and fprop().
real PLearn::LayerCostModule::average_deriv [protected] |
Definition at line 205 of file LayerCostModule.h.
Referenced by bpropUpdate(), and forget().
bool PLearn::LayerCostModule::bprop_all_terms [protected] |
Boolean determined by the optimization_strategy.
Definition at line 194 of file LayerCostModule.h.
Referenced by bpropUpdate(), and build_().
TVec< TVec< Vec > > PLearn::LayerCostModule::cache_differ_count_i [protected] |
Definition at line 214 of file LayerCostModule.h.
Referenced by build_(), computeKLdiv(), delta_KLdivTerm(), and makeDeepCopyFromShallowCopy().
TVec< TVec< Vec > > PLearn::LayerCostModule::cache_differ_count_j [protected] |
Definition at line 215 of file LayerCostModule.h.
Referenced by build_(), computeKLdiv(), delta_KLdivTerm(), and makeDeepCopyFromShallowCopy().
TVec< TVec< Vec > > PLearn::LayerCostModule::cache_n_differ [protected] |
Definition at line 216 of file LayerCostModule.h.
Referenced by build_(), computeKLdiv(), delta_KLdivTerm(), and makeDeepCopyFromShallowCopy().
Generic name of the cost function.
Definition at line 59 of file LayerCostModule.h.
Referenced by bpropUpdate(), build_(), declareOptions(), and fprop().
The generic name of the cost function.
Definition at line 103 of file LayerCostModule.h.
Referenced by build_(), and declareOptions().
bool PLearn::LayerCostModule::EXP_FUNC [protected] |
Definition at line 187 of file LayerCostModule.h.
Referenced by build_(), deriv_func_(), and func_().
For non stochastic KL divergence cost function.
Definition at line 74 of file LayerCostModule.h.
Referenced by bpropUpdate(), build_(), computeHisto(), computeKLdiv(), computeSafeHisto(), declareOptions(), delta_KLdivTerm(), delta_SafeKLdivTerm(), fprop(), and histo_index().
real PLearn::LayerCostModule::HISTO_STEP [protected] |
Variables for (non stochastic) KL Div cost function.
--------------------------------------------------- Range of a histogram's bin ( HISTO_STEP = 1/histo_size )
Definition at line 210 of file LayerCostModule.h.
Referenced by build_(), computeKLdiv(), delta_KLdivTerm(), and dq().
Definition at line 90 of file LayerCostModule.h.
Referenced by bpropUpdate(), computeCorrelationStatistics(), forget(), and makeDeepCopyFromShallowCopy().
only for 'correlation' cost function
Definition at line 89 of file LayerCostModule.h.
Referenced by bpropUpdate(), computeCorrelationStatistics(), computePascalStatistics(), forget(), and makeDeepCopyFromShallowCopy().
Definition at line 96 of file LayerCostModule.h.
Referenced by build_(), computeCorrelationStatistics(), computePascalStatistics(), declareOptions(), forget(), and makeDeepCopyFromShallowCopy().
Statistics on inputs (estimated empiricially on some data) Computed only when cost_function == 'correlation' or (for some) 'pascal'.
Definition at line 86 of file LayerCostModule.h.
Referenced by bpropUpdate(), computeCorrelationStatistics(), computePascalStatistics(), forget(), and makeDeepCopyFromShallowCopy().
only for 'correlation' cost function
Variables for (non stochastic) Pascal's/correlation function with momentum ------------------------------------------------------------- Statistics on outputs (estimated empiricially on the data)
Definition at line 95 of file LayerCostModule.h.
Referenced by build_(), computeCorrelationStatistics(), computePascalStatistics(), declareOptions(), forget(), and makeDeepCopyFromShallowCopy().
Histograms of inputs (estimated empiricially on some data) Computed only when cost_function == 'kl_div' or 'kl_div_simpe'.
Definition at line 81 of file LayerCostModule.h.
Referenced by build_(), computeHisto(), computeKLdiv(), computeSafeHisto(), delta_KLdivTerm(), delta_SafeKLdivTerm(), forget(), and makeDeepCopyFromShallowCopy().
Definition at line 87 of file LayerCostModule.h.
Referenced by bpropUpdate(), computeCorrelationStatistics(), forget(), and makeDeepCopyFromShallowCopy().
Does stochastic gradient (without memory of the past) makes sense with our cost function?
Definition at line 199 of file LayerCostModule.h.
bool PLearn::LayerCostModule::LINEAR_FUNC [protected] |
Definition at line 184 of file LayerCostModule.h.
Referenced by build_(), deriv_func_(), and func_().
bool PLearn::LayerCostModule::LOG_FUNC [protected] |
Definition at line 188 of file LayerCostModule.h.
Referenced by build_(), deriv_func_(), and func_().
Parameter to compute moving means in non stochastic cost functions.
Definition at line 65 of file LayerCostModule.h.
Referenced by bpropUpdate(), build_(), computeCorrelationStatistics(), computePascalStatistics(), declareOptions(), and forget().
real PLearn::LayerCostModule::norm_factor [protected] |
Normalizing factor applied to the cost function to take into acount the number of weights.
Definition at line 203 of file LayerCostModule.h.
Referenced by bpropUpdate(), build_(), computeKLdiv(), delta_KLdivTerm(), and fprop().
Maximum number of stages we want to propagate the gradient.
Definition at line 62 of file LayerCostModule.h.
Referenced by bpropUpdate(), and declareOptions().
real PLearn::LayerCostModule::one_count [mutable, protected] |
the weight of a sample within a batch (usually, 1/n_samples)
Definition at line 213 of file LayerCostModule.h.
Referenced by computeCorrelationStatistics(), computeHisto(), computePascalStatistics(), computeSafeHisto(), delta_KLdivTerm(), delta_SafeKLdivTerm(), and forget().
Kind of optimization.
Definition at line 68 of file LayerCostModule.h.
Referenced by build_(), and declareOptions().
The function applied to the local cost between 2 inputs to obtain the global cost (after averaging)
Definition at line 100 of file LayerCostModule.h.
Referenced by build_(), and declareOptions().
map<string, int> PLearn::LayerCostModule::portname_to_index [protected] |
Map from a port name to its index in the 'ports' vector.
Definition at line 219 of file LayerCostModule.h.
Referenced by addPortName(), build_(), and getPortIndex().
TVec<string> PLearn::LayerCostModule::ports [protected] |
List of port names.
Definition at line 222 of file LayerCostModule.h.
Referenced by addPortName(), build_(), getPorts(), and makeDeepCopyFromShallowCopy().
bool PLearn::LayerCostModule::POW4_FUNC [protected] |
Definition at line 186 of file LayerCostModule.h.
Referenced by build_(), deriv_func_(), and func_().
Definition at line 195 of file LayerCostModule.h.
Referenced by bpropUpdate(), and build_().
bool PLearn::LayerCostModule::SQUARE_FUNC [protected] |
Definition at line 185 of file LayerCostModule.h.
Referenced by build_(), deriv_func_(), and func_().
int PLearn::LayerCostModule::stage [protected] |
Number of stage the BPropAccUpdate function was called.
Definition at line 191 of file LayerCostModule.h.
Referenced by bpropUpdate(), declareOptions(), and forget().
 1.7.4
1.7.4