|
PLearn 0.1
|
|
PLearn 0.1
|
Neural net, learned layer-wise in a greedy fashion. More...
#include <DeepBeliefNet.h>

Public Member Functions | |
| DeepBeliefNet () | |
| Default constructor. | |
| virtual int | outputsize () const |
| Returns the size of this learner's output, (which typically may depend on its inputsize(), targetsize() and set options). | |
| virtual void | forget () |
| (Re-)initializes the PLearner in its fresh state (that state may depend on the 'seed' option) and sets 'stage' back to 0 (this is the stage of a fresh learner!). | |
| virtual void | train () |
| The role of the train method is to bring the learner up to stage==nstages, updating the train_stats collector with training costs measured on-line in the process. | |
| virtual void | test (VMat testset, PP< VecStatsCollector > test_stats, VMat testoutputs=0, VMat testcosts=0) const |
| Re-implementation of the PLearner test() for profiling purposes. | |
| virtual void | computeOutput (const Vec &input, Vec &output) const |
| Computes the output from the input. | |
| virtual void | computeOutputsAndCosts (const Mat &inputs, const Mat &targets, Mat &outputs, Mat &costs) const |
| This function is usefull when the NLL CostModule AND/OR the final_cost Module are more efficient with batch computation (or need to be computed on a bunch of examples, as LayerCostModule) | |
| virtual void | computeCostsFromOutputs (const Vec &input, const Vec &output, const Vec &target, Vec &costs) const |
| Computes the costs from already computed output. | |
| virtual void | computeClassifAndFinalCostsFromOutputs (const Mat &inputs, const Mat &outputs, const Mat &targets, Mat &costs) const |
| virtual TVec< std::string > | getTestCostNames () const |
| Returns the names of the costs computed by computeCostsFromOutpus (and thus the test method). | |
| virtual TVec< std::string > | getTrainCostNames () const |
| Returns the names of the objective costs that the train method computes and for which it updates the VecStatsCollector train_stats. | |
| void | onlineStep (const Vec &input, const Vec &target, Vec &train_costs) |
| void | onlineStep (const Mat &inputs, const Mat &targets, Mat &train_costs) |
| void | greedyStep (const Vec &input, const Vec &target, int index) |
| void | greedyStep (const Mat &inputs, const Mat &targets, int index, Mat &train_costs_m) |
| void | jointGreedyStep (const Vec &input, const Vec &target) |
| void | jointGreedyStep (const Mat &inputs, const Mat &targets) |
| void | upDownStep (const Vec &input, const Vec &target, Vec &train_costs) |
| void | upDownStep (const Mat &inputs, const Mat &targets, Mat &train_costs) |
| void | fineTuningStep (const Vec &input, const Vec &target, Vec &train_costs) |
| void | fineTuningStep (const Mat &inputs, const Mat &targets, Mat &train_costs) |
| void | contrastiveDivergenceStep (const PP< RBMLayer > &down_layer, const PP< RBMConnection > &connection, const PP< RBMLayer > &up_layer, int layer_index, bool nofprop=false) |
| Perform a step of contrastive divergence, assuming that down_layer->expectation(s) is set. | |
| virtual string | classname () const |
| virtual OptionList & | getOptionList () const |
| virtual OptionMap & | getOptionMap () const |
| virtual RemoteMethodMap & | getRemoteMethodMap () const |
| virtual DeepBeliefNet * | deepCopy (CopiesMap &copies) const |
| virtual void | build () |
| Finish building the object; just call inherited::build followed by build_() | |
| virtual void | makeDeepCopyFromShallowCopy (CopiesMap &copies) |
| Transforms a shallow copy into a deep copy. | |
Static Public Member Functions | |
| static string | _classname_ () |
| static OptionList & | _getOptionList_ () |
| static RemoteMethodMap & | _getRemoteMethodMap_ () |
| static Object * | _new_instance_for_typemap_ () |
| static bool | _isa_ (const Object *o) |
| static void | _static_initialize_ () |
| static const PPath & | declaringFile () |
Public Attributes | |
| real | cd_learning_rate |
| The learning rate used during contrastive divergence learning. | |
| real | cd_decrease_ct |
| The decrease constant of the learning rate used during contrastive divergence learning. | |
| real | up_down_learning_rate |
| The learning rate used in the up-down algorithm during the unsupervised fine tuning gradient descent. | |
| real | up_down_decrease_ct |
| The decrease constant of the learning rate used in the up-down algorithm during the unsupervised fine tuning gradient descent. | |
| real | grad_learning_rate |
| The learning rate used during the gradient descent. | |
| real | grad_decrease_ct |
| The decrease constant of the learning rate used during gradient descent. | |
| int | batch_size |
| Training batch size (1=stochastic learning, 0=full batch learning) | |
| int | n_classes |
| Number of classes in the training set. | |
| TVec< int > | training_schedule |
| Number of examples to use during each phase of learning: first the greedy phases, and then the fine-tuning phase. | |
| int | up_down_nstages |
| Number of samples to use for unsupervised fine-tuning with the up-down algorithm. | |
| bool | use_classification_cost |
| If the first cost function is the NLL in classification, pre-trained with CD, and using the last *two* layers to get a better approximation (undirected softmax) than layer-wise mean-field. | |
| bool | reconstruct_layerwise |
| Minimize reconstruction error of each layer as an auto-encoder. | |
| TVec< PP< RBMLayer > > | layers |
| The layers of units in the network. | |
| int | i_output_layer |
| The index of the output layer (when the final module is external) | |
| string | learnerExpdir |
| Experiment directory where the learner will be save if save_learner_before_fine_tuning is true. | |
| bool | save_learner_before_fine_tuning |
| Saves the learner before the supervised fine_tuning. | |
| TVec< PP< RBMConnection > > | connections |
| The weights of the connections between the layers. | |
| TVec< PP< RBMMultinomialLayer > > | greedy_target_layers |
| Optional target layers for greedy layer-wise pretraining. | |
| TVec< PP< RBMMatrixConnection > > | greedy_target_connections |
| Optional target matrix connections for greedy layer-wise pretraining. | |
| PP< OnlineLearningModule > | final_module |
| Optional module that takes as input the output of the last layer (layers[n_layers-1), and its output is fed to final_cost, and concatenated with the one of classification_cost (if present) as output of the learner. | |
| PP< CostModule > | final_cost |
| The cost function to be applied on top of the DBN (or of final_module if provided). | |
| TVec< PP< CostModule > > | partial_costs |
| The different cost function to be applied on top of each layer (except the first one, which has to be null) of the RBM. | |
| bool | use_sample_for_up_layer |
| Indication that the update of the top layer during CD uses a sample, not the expectation. | |
| string | use_corrupted_posDownVal |
| Indicates whether we will use a corrupted version of the positive down value during the CD step. | |
| string | noise_type |
| Type of noise that corrupts the pos_down_val. | |
| real | fraction_of_masked_inputs |
| Fraction of components that will be corrupted in function corrupt_input. | |
| bool | mask_with_pepper_salt |
| Indication that inputs should be masked with 0 or 1 according to prop_salt_noise. | |
| real | prob_salt_noise |
| Probability that we mask by 1 instead of 0 when using mask_with_pepper_salt. | |
| PP< RBMClassificationModule > | classification_module |
| The module computing the probabilities of the different classes. | |
| int | n_layers |
| Number of layers. | |
| TVec< string > | cost_names |
| The computed cost names. | |
| bool | online |
| whether to do things by stages, including fine-tuning, or on-line | |
| real | background_gibbs_update_ratio |
| bool | top_layer_joint_cd |
| Wether we do a step of joint contrastive divergence on top-layer Only used if online for the moment. | |
| int | gibbs_chain_reinit_freq |
| after how many examples should we re-initialize the Gibbs chains (if == INT_MAX, the default then NEVER re-initialize except when stage==0) | |
| real | mean_field_contrastive_divergence_ratio |
| Coefficient between 0 and 1. | |
| int | train_stats_window |
| The number of samples to use to compute training stats. | |
| PP< PTimer > | timer |
| Timer for monitoring the speed. | |
| PP< NLLCostModule > | classification_cost |
| The module computing the classification cost function (NLL) on top of classification_module. | |
| PP< RBMMixedLayer > | joint_layer |
| Concatenation of layers[n_layers-2] and the target layer (that is inside classification_module), if use_classification_cost. | |
Static Public Attributes | |
| static StaticInitializer | _static_initializer_ |
Static Protected Member Functions | |
| static void | declareOptions (OptionList &ol) |
| Declares the class options. | |
| static void | declareMethods (RemoteMethodMap &rmm) |
| Declare the methods that are remote-callable. | |
Protected Attributes | |
| int | minibatch_size |
| Actual size of a mini-batch (size of the training set if batch_size==1) | |
| bool | initialize_gibbs_chain |
| TVec< Vec > | activation_gradients |
| Stores the gradient of the cost wrt the activations (at the input of the layers) | |
| TVec< Mat > | activations_gradients |
| For mini-batch. | |
| TVec< Vec > | expectation_gradients |
| Stores the gradient of the cost wrt the expectations (at the output of the layers) | |
| TVec< Mat > | expectations_gradients |
| For mini-batch. | |
| TVec< TVec< Vec > > | greedy_target_expectations |
| For the fprop with greedy_target_layers. | |
| TVec< TVec< Vec > > | greedy_target_activations |
| TVec< TVec< Vec > > | greedy_target_expectation_gradients |
| TVec< TVec< Vec > > | greedy_target_activation_gradients |
| TVec< Vec > | greedy_target_probability_gradients |
| TVec< PP< RBMLayer > > | greedy_joint_layers |
| TVec< PP< RBMConnection > > | greedy_joint_connections |
| Vec | final_cost_input |
| Mat | final_cost_inputs |
| For mini-batch. | |
| Vec | final_cost_value |
| Mat | final_cost_values |
| For mini-batch. | |
| Vec | final_cost_output |
| Vec | class_output |
| Vec | class_gradient |
| Vec | final_cost_gradient |
| Stores the gradient of the cost at the input of final_cost. | |
| Mat | final_cost_gradients |
| For mini-batch. | |
| Vec | save_layer_activation |
| buffers bottom layer activation during onlineStep | |
| Mat | save_layer_activations |
| For mini-batches. | |
| Vec | save_layer_expectation |
| buffers bottom layer expectation during onlineStep | |
| Mat | save_layer_expectations |
| For mini-batches. | |
| Vec | pos_down_val |
| Store a copy of the positive phase values. | |
| Vec | corrupted_pos_down_val |
| Vec | pos_up_val |
| Mat | pos_down_vals |
| Mat | pos_up_vals |
| Mat | cd_neg_down_vals |
| Mat | cd_neg_up_vals |
| Mat | mf_cd_neg_down_vals |
| Mat | mf_cd_neg_up_vals |
| Vec | mf_cd_neg_down_val |
| Vec | mf_cd_neg_up_val |
| TVec< Mat > | gibbs_down_state |
| Store the state of the Gibbs chain for each RBM. | |
| Vec | optimized_costs |
| Used to store the costs optimized by the final cost module. | |
| Vec | target_one_hot |
| One-hot representation of the target. | |
| Vec | reconstruction_costs |
| Stores reconstruction costs. | |
| int | nll_cost_index |
| Keeps the index of the NLL cost in train_costs. | |
| int | class_cost_index |
| Keeps the index of the class_error cost in train_costs. | |
| int | final_cost_index |
| Keeps the beginning index of the final costs in train_costs. | |
| TVec< int > | partial_costs_indices |
| Keeps the beginning indices of the partial costs in train_costs. | |
| int | reconstruction_cost_index |
| Keeps the beginning index of the reconstruction costs in train_costs. | |
| int | greedy_target_layer_nlls_index |
| Keeps the beginning index of the greedy target layer NLLs. | |
| int | training_cpu_time_cost_index |
| Index of the cpu time cost (per each call of train()) | |
| int | cumulative_training_time_cost_index |
| The index of the cumulative training time cost. | |
| int | cumulative_testing_time_cost_index |
| The index of the cumulative testing time cost. | |
| real | cumulative_training_time |
| Holds the total training (cpu)time. | |
| real | cumulative_testing_time |
| Holds the total testing (cpu)time. | |
| TVec< int > | cumulative_schedule |
| Cumulative training schedule. | |
| int | up_down_stage |
| Number of samples visited so far during unsupervised fine-tuning. | |
| Vec | layer_input |
| Mat | layer_inputs |
| TVec< PP< RBMConnection > > | generative_connections |
| The untied generative weights of the connections between the layers for the up-down algorithm. | |
| TVec< Vec > | up_sample |
| TVec< Vec > | down_sample |
| TVec< TVec< int > > | expectation_indices |
| Indices of the expectation components. | |
Private Types | |
| typedef PLearner | inherited |
Private Member Functions | |
| void | build_ () |
| This does the actual building. | |
| void | build_layers_and_connections () |
| void | build_costs () |
| void | build_classification_cost () |
| void | build_final_cost () |
| void | corrupt_input (const Vec &input, Vec &corrupted_input, int layer) |
| void | setLearningRate (real the_learning_rate) |
| TVec< Vec > | fantasizeKTime (const int KTime, const Vec &srcImg, const Vec &sample, bool alwaysFromSrcImg) |
| TVec< Vec > | fantasizeKTimeOnMultiSrcImg (const int KTime, const Mat &srcImg, const Vec &sample, bool alwaysFromSrcImg) |
Neural net, learned layer-wise in a greedy fashion.
This version support different unit types, different connection types, and different cost functions, including the NLL in classification.
Definition at line 61 of file DeepBeliefNet.h.
typedef PLearner PLearn::DeepBeliefNet::inherited [private] |
Reimplemented from PLearn::PLearner.
Definition at line 63 of file DeepBeliefNet.h.
| PLearn::DeepBeliefNet::DeepBeliefNet | ( | ) |
Default constructor.
Definition at line 60 of file DeepBeliefNet.cc.
References n_layers, and PLearn::PLearner::random_gen.
:
cd_learning_rate( 0. ),
cd_decrease_ct( 0. ),
up_down_learning_rate( 0. ),
up_down_decrease_ct( 0. ),
grad_learning_rate( 0. ),
grad_decrease_ct( 0. ),
// grad_weight_decay( 0. ),
batch_size( 1 ),
n_classes( -1 ),
up_down_nstages( 0 ),
use_classification_cost( true ),
reconstruct_layerwise( false ),
i_output_layer( -1 ),
learnerExpdir(""),
save_learner_before_fine_tuning( false ),
use_sample_for_up_layer( false ),
use_corrupted_posDownVal( "none" ),
noise_type( "masking_noise" ),
fraction_of_masked_inputs( 0 ),
mask_with_pepper_salt( false ),
prob_salt_noise( 0.5 ),
online ( false ),
background_gibbs_update_ratio(0),
gibbs_chain_reinit_freq( INT_MAX ),
mean_field_contrastive_divergence_ratio( 0 ),
train_stats_window( -1 ),
minibatch_size( 0 ),
initialize_gibbs_chain( false ),
nll_cost_index( -1 ),
class_cost_index( -1 ),
final_cost_index( -1 ),
reconstruction_cost_index( -1 ),
training_cpu_time_cost_index ( -1 ),
cumulative_training_time_cost_index ( -1 ),
cumulative_testing_time_cost_index ( -1 ),
cumulative_training_time( 0 ),
cumulative_testing_time( 0 ),
up_down_stage( 0 )
{
random_gen = new PRandom();
n_layers = 0;
}
| string PLearn::DeepBeliefNet::_classname_ | ( | ) | [static] |
Reimplemented from PLearn::PLearner.
Definition at line 55 of file DeepBeliefNet.cc.
| OptionList & PLearn::DeepBeliefNet::_getOptionList_ | ( | ) | [static] |
Reimplemented from PLearn::PLearner.
Definition at line 55 of file DeepBeliefNet.cc.
| RemoteMethodMap & PLearn::DeepBeliefNet::_getRemoteMethodMap_ | ( | ) | [static] |
Reimplemented from PLearn::PLearner.
Definition at line 55 of file DeepBeliefNet.cc.
Reimplemented from PLearn::PLearner.
Definition at line 55 of file DeepBeliefNet.cc.
| Object * PLearn::DeepBeliefNet::_new_instance_for_typemap_ | ( | ) | [static] |
Reimplemented from PLearn::Object.
Definition at line 55 of file DeepBeliefNet.cc.
| StaticInitializer DeepBeliefNet::_static_initializer_ & PLearn::DeepBeliefNet::_static_initialize_ | ( | ) | [static] |
Reimplemented from PLearn::PLearner.
Definition at line 55 of file DeepBeliefNet.cc.
| void PLearn::DeepBeliefNet::build | ( | ) | [virtual] |
Finish building the object; just call inherited::build followed by build_()
Reimplemented from PLearn::PLearner.
Definition at line 943 of file DeepBeliefNet.cc.
References PLearn::PLearner::build(), and build_().
{
inherited::build();
build_();
}
| void PLearn::DeepBeliefNet::build_ | ( | ) | [private] |
This does the actual building.
Reimplemented from PLearn::PLearner.
Definition at line 451 of file DeepBeliefNet.cc.
References PLearn::Profiler::activate(), background_gibbs_update_ratio, batch_size, build_costs(), build_layers_and_connections(), cumulative_schedule, PLearn::endl(), PLearn::TVec< T >::fill(), i, i_output_layer, PLearn::TVec< T >::isEmpty(), layers, PLearn::TVec< T >::length(), mean_field_contrastive_divergence_ratio, n_layers, online, PLASSERT, PLERROR, PLWARNING, PLearn::TVec< T >::resize(), training_schedule, up_down_nstages, use_corrupted_posDownVal, and use_sample_for_up_layer.
Referenced by build().
{
PLASSERT( batch_size >= 0 );
MODULE_LOG << "build_() called" << endl;
// Initialize some learnt variables
if (layers.isEmpty())
PLERROR("In DeepBeliefNet::build_ - You must provide at least one RBM "
"layer through the 'layers' option");
else
n_layers = layers.length();
if( i_output_layer < 0)
i_output_layer = n_layers - 1;
if( online && up_down_nstages > 0)
PLERROR("In DeepBeliefNet::build_ - up-down algorithm not implemented "
"for online setting.");
if( batch_size != 1 && up_down_nstages > 0 )
PLERROR("In DeepBeliefNet::build_ - up-down algorithm not implemented "
"for minibatch setting.");
if( mean_field_contrastive_divergence_ratio > 0 &&
background_gibbs_update_ratio != 0 )
PLERROR("In DeepBeliefNet::build_ - mean-field CD cannot be used "
"with background_gibbs_update_ratio != 0.");
if( mean_field_contrastive_divergence_ratio > 0 &&
use_sample_for_up_layer )
PLERROR("In DeepBeliefNet::build_ - mean-field CD cannot be used "
"with use_sample_for_up_layer.");
if( mean_field_contrastive_divergence_ratio < 0 ||
mean_field_contrastive_divergence_ratio > 1 )
PLERROR("In DeepBeliefNet::build_ - mean_field_contrastive_divergence_ratio should "
"be in [0,1].");
if( use_corrupted_posDownVal != "for_cd_fprop" &&
use_corrupted_posDownVal != "for_cd_update" &&
use_corrupted_posDownVal != "none" )
PLERROR("In DeepBeliefNet::build_ - use_corrupted_posDownVal should "
"be chosen among {\"for_cd_fprop\",\"for_cd_update\",\"none\"}.");
if( !online )
{
if( training_schedule.length() != n_layers )
{
PLWARNING("In DeepBeliefNet::build_ - training_schedule.length() "
"!= n_layers, resizing and zeroing");
training_schedule.resize( n_layers );
training_schedule.fill( 0 );
}
cumulative_schedule.resize( n_layers+1 );
cumulative_schedule[0] = 0;
for( int i=0 ; i<n_layers ; i++ )
{
cumulative_schedule[i+1] = cumulative_schedule[i] +
training_schedule[i];
}
}
build_layers_and_connections();
// Activate the profiler
Profiler::activate();
build_costs();
}

| void PLearn::DeepBeliefNet::build_classification_cost | ( | ) | [private] |
Definition at line 805 of file DeepBeliefNet.cc.
References batch_size, classification_cost, classification_module, connections, PLearn::endl(), joint_layer, layers, n_classes, n_layers, PLASSERT_MSG, PLearn::PLearner::random_gen, and PLearn::TVec< T >::size().
Referenced by build_costs().
{
MODULE_LOG << "build_classification_cost() called" << endl;
PLASSERT_MSG(batch_size == 1, "DeepBeliefNet::build_classification_cost - "
"This method has not been verified yet for minibatch "
"compatibility");
PP<RBMMatrixConnection> last_to_target;
if (classification_module)
last_to_target = classification_module->last_to_target;
if (!last_to_target ||
last_to_target->up_size != layers[n_layers-1]->size ||
last_to_target->down_size != n_classes ||
last_to_target->random_gen != random_gen)
{
// We need to (re-)create 'last_to_target', and thus the classification
// module too.
// This is not systematically done so that the learner can be
// saved and loaded without losing learned parameters.
last_to_target = new RBMMatrixConnection();
last_to_target->up_size = layers[n_layers-1]->size;
last_to_target->down_size = n_classes;
last_to_target->random_gen = random_gen;
last_to_target->build();
PP<RBMMultinomialLayer> target_layer = new RBMMultinomialLayer();
target_layer->size = n_classes;
target_layer->random_gen = random_gen;
target_layer->build();
PLASSERT_MSG(n_layers >= 2, "You must specify at least two layers (the "
"input layer and one hidden layer)");
classification_module = new RBMClassificationModule();
classification_module->previous_to_last = connections[n_layers-2];
classification_module->last_layer =
(RBMBinomialLayer*) (RBMLayer*) layers[n_layers-1];
classification_module->last_to_target = last_to_target;
classification_module->target_layer = target_layer;
classification_module->random_gen = random_gen;
classification_module->build();
}
classification_cost = new NLLCostModule();
classification_cost->input_size = n_classes;
classification_cost->target_size = 1;
classification_cost->build();
joint_layer = new RBMMixedLayer();
joint_layer->sub_layers.resize( 2 );
joint_layer->sub_layers[0] = layers[ n_layers-2 ];
joint_layer->sub_layers[1] = classification_module->target_layer;
joint_layer->random_gen = random_gen;
joint_layer->build();
}


| void PLearn::DeepBeliefNet::build_costs | ( | ) | [private] |
Definition at line 526 of file DeepBeliefNet.cc.
References PLearn::TVec< T >::append(), build_classification_cost(), build_final_cost(), class_cost_index, cost_names, cumulative_testing_time_cost_index, cumulative_training_time_cost_index, final_cost, final_cost_index, greedy_target_layer_nlls_index, greedy_target_layers, i, PLearn::TVec< T >::isEmpty(), j, PLearn::TVec< T >::length(), n_classes, n_layers, nll_cost_index, partial_costs, partial_costs_indices, PLASSERT, PLERROR, PLearn::PLearner::random_gen, reconstruct_layerwise, reconstruction_cost_index, reconstruction_costs, PLearn::TVec< T >::resize(), target_one_hot, PLearn::tostring(), training_cpu_time_cost_index, and use_classification_cost.
Referenced by build_().
{
cost_names.resize(0);
int current_index = 0;
// build the classification module, its cost and the joint layer
if( use_classification_cost )
{
PLASSERT( n_classes >= 2 );
build_classification_cost();
cost_names.append("NLL");
nll_cost_index = current_index;
current_index++;
cost_names.append("class_error");
class_cost_index = current_index;
current_index++;
}
if( final_cost )
{
build_final_cost();
TVec<string> final_names = final_cost->costNames();
int n_final_costs = final_names.length();
for( int i=0; i<n_final_costs; i++ )
cost_names.append("final." + final_names[i]);
final_cost_index = current_index;
current_index += n_final_costs;
}
if( partial_costs )
{
int n_partial_costs = partial_costs.length();
if( n_partial_costs != n_layers - 1)
PLERROR("DeepBeliefNet::build_costs() - \n"
"partial_costs.length() (%d) != n_layers-1 (%d).\n",
n_partial_costs, n_layers-1);
partial_costs_indices.resize(n_partial_costs);
for( int i=0; i<n_partial_costs; i++ )
if( partial_costs[i] )
{
TVec<string> names = partial_costs[i]->costNames();
int n_partial_costs_i = names.length();
for( int j=0; j<n_partial_costs_i; j++ )
cost_names.append("partial"+tostring(i)+"."+names[j]);
partial_costs_indices[i] = current_index;
current_index += n_partial_costs_i;
// Share random_gen with partial_costs[i], unless it already
// has one
if( !(partial_costs[i]->random_gen) )
{
partial_costs[i]->random_gen = random_gen;
partial_costs[i]->forget();
}
}
else
partial_costs_indices[i] = -1;
}
else
partial_costs_indices.resize(0);
if( reconstruct_layerwise )
{
reconstruction_costs.resize(n_layers);
cost_names.append("layerwise_reconstruction_error");
reconstruction_cost_index = current_index;
current_index++;
for( int i=0; i<n_layers-1; i++ )
cost_names.append("layer"+tostring(i)+".reconstruction_error");
current_index += n_layers-1;
}
else
reconstruction_costs.resize(0);
if( !greedy_target_layers.isEmpty() )
{
greedy_target_layer_nlls_index = current_index;
target_one_hot.resize(n_classes);
for( int i=0; i<n_layers-1; i++ )
{
cost_names.append("layer"+tostring(i)+".nll");
current_index++;
}
}
cost_names.append("cpu_time");
cost_names.append("cumulative_train_time");
cost_names.append("cumulative_test_time");
training_cpu_time_cost_index = current_index;
current_index++;
cumulative_training_time_cost_index = current_index;
current_index++;
cumulative_testing_time_cost_index = current_index;
current_index++;
PLASSERT( current_index == cost_names.length() );
}

| void PLearn::DeepBeliefNet::build_final_cost | ( | ) | [private] |
Definition at line 865 of file DeepBeliefNet.cc.
References PLearn::endl(), final_cost, final_cost_gradient, final_module, grad_learning_rate, layers, n_classes, n_layers, PLASSERT_MSG, PLERROR, PLearn::PLearner::random_gen, PLearn::TVec< T >::resize(), PLearn::PLearner::targetsize(), and PLearn::PLearner::targetsize_.
Referenced by build_costs().
{
MODULE_LOG << "build_final_cost() called" << endl;
PLASSERT_MSG(final_cost->input_size >= 0, "The input size of the final "
"cost must be non-negative");
final_cost_gradient.resize( final_cost->input_size );
final_cost->setLearningRate( grad_learning_rate );
if( final_module )
{
if( layers[n_layers-1]->size != final_module->input_size )
PLERROR("DeepBeliefNet::build_final_cost() - "
"layers[%i]->size (%d) != final_module->input_size (%d)."
"\n", n_layers-1, layers[n_layers-1]->size,
final_module->input_size);
if( final_module->output_size != final_cost->input_size )
PLERROR("DeepBeliefNet::build_final_cost() - "
"final_module->output_size (%d) != final_cost->input_size (%d)."
"\n", final_module->output_size,
final_module->input_size);
final_module->setLearningRate( grad_learning_rate );
// Share random_gen with final_module, unless it already has one
if( !(final_module->random_gen) )
{
final_module->random_gen = random_gen;
final_module->forget();
}
// check target size and final_cost->input_size
if( n_classes == 0 ) // regression
{
if( targetsize_ >= 0 && final_cost->input_size != targetsize() )
PLERROR("DeepBeliefNet::build_final_cost() - "
"final_cost->input_size (%d) != targetsize() (%d), "
"although we are doing regression (n_classes == 0).\n",
final_cost->input_size, targetsize());
}
else
{
if( final_cost->input_size != n_classes )
PLERROR("DeepBeliefNet::build_final_cost() - "
"final_cost->input_size (%d) != n_classes (%d), "
"although we are doing classification (n_classes != 0).\n",
final_cost->input_size, n_classes);
if( targetsize_ >= 0 && targetsize() != 1 )
PLERROR("DeepBeliefNet::build_final_cost() - "
"targetsize() (%d) != 1, "
"although we are doing classification (n_classes != 0).\n",
targetsize());
}
}
else
{
if( layers[n_layers-1]->size != final_cost->input_size )
PLERROR("DeepBeliefNet::build_final_cost() - "
"layers[%i]->size (%d) != final_cost->input_size (%d)."
"\n", n_layers-1, layers[n_layers-1]->size,
final_cost->input_size);
}
// Share random_gen with final_cost, unless it already has one
if( !(final_cost->random_gen) )
{
final_cost->random_gen = random_gen;
final_cost->forget();
}
}


| void PLearn::DeepBeliefNet::build_layers_and_connections | ( | ) | [private] |
Definition at line 637 of file DeepBeliefNet.cc.
References activation_gradients, activations_gradients, background_gibbs_update_ratio, batch_size, c, connections, PLearn::endl(), expectation_gradients, expectation_indices, expectations_gradients, fraction_of_masked_inputs, gibbs_down_state, greedy_joint_connections, greedy_joint_layers, greedy_target_activation_gradients, greedy_target_activations, greedy_target_connections, greedy_target_expectation_gradients, greedy_target_expectations, greedy_target_layers, greedy_target_probability_gradients, i, PLearn::PLearner::inputsize(), PLearn::PLearner::inputsize_, PLearn::TVec< T >::isEmpty(), j, layers, PLearn::TVec< T >::length(), minibatch_hack, n_classes, n_layers, noise_type, online, partial_costs, PLASSERT, PLASSERT_MSG, PLERROR, PLearn::PLearner::random_gen, PLearn::TVec< T >::resize(), PLearn::TVec< T >::size(), use_classification_cost, and use_corrupted_posDownVal.
Referenced by build_().
{
MODULE_LOG << "build_layers_and_connections() called" << endl;
if( connections.length() != n_layers-1 )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"connections.length() (%d) != n_layers-1 (%d).\n",
connections.length(), n_layers-1);
if( inputsize_ >= 0 )
PLASSERT( layers[0]->size == inputsize() );
activation_gradients.resize( n_layers );
activations_gradients.resize( n_layers );
expectation_gradients.resize( n_layers );
expectations_gradients.resize( n_layers );
gibbs_down_state.resize( n_layers-1 );
expectation_indices.resize( n_layers-1 );
for( int i=0 ; i<n_layers-1 ; i++ )
{
if( layers[i]->size != connections[i]->down_size )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"layers[%i]->size (%d) != connections[%i]->down_size (%d)."
"\n", i, layers[i]->size, i, connections[i]->down_size);
if( connections[i]->up_size != layers[i+1]->size )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"connections[%i]->up_size (%d) != layers[%i]->size (%d)."
"\n", i, connections[i]->up_size, i+1, layers[i+1]->size);
// Assign random_gen to layers[i] and connections[i], unless they
// already have one
if( !(layers[i]->random_gen) )
{
layers[i]->random_gen = random_gen;
layers[i]->forget();
}
if( !(connections[i]->random_gen) )
{
connections[i]->random_gen = random_gen;
connections[i]->forget();
}
activation_gradients[i].resize( layers[i]->size );
expectation_gradients[i].resize( layers[i]->size );
if( greedy_target_layers.length()>i && greedy_target_layers[i] )
{
if( use_classification_cost )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"use_classification_cost not implemented for greedy_target_layers.");
if( greedy_target_connections.length()>i && !greedy_target_connections[i] )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"some greedy_target_connections are missing.");
if( greedy_target_layers[i]->size != n_classes)
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"greedy_target_layers[%d] should be of size %d.",i,n_classes);
if( greedy_target_connections[i]->down_size != n_classes ||
greedy_target_connections[i]->up_size != layers[i+1]->size )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"greedy_target_connections[%d] should be of size (%d,%d).",
i,layers[i+1]->size,n_classes);
if( partial_costs.length() != 0 )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"greedy_target_layers can't be used with partial_costs.");
greedy_target_expectations.resize(n_layers-1);
greedy_target_activations.resize(n_layers-1);
greedy_target_expectation_gradients.resize(n_layers-1);
greedy_target_activation_gradients.resize(n_layers-1);
greedy_target_probability_gradients.resize(n_layers-1);
greedy_target_expectations[i].resize(n_classes);
greedy_target_activations[i].resize(n_classes);
greedy_target_expectation_gradients[i].resize(n_classes);
greedy_target_activation_gradients[i].resize(n_classes);
greedy_target_probability_gradients[i].resize(n_classes);
for( int c=0; c<n_classes; c++)
{
greedy_target_expectations[i][c].resize(layers[i+1]->size);
greedy_target_activations[i][c].resize(layers[i+1]->size);
greedy_target_expectation_gradients[i][c].resize(layers[i+1]->size);
greedy_target_activation_gradients[i][c].resize(layers[i+1]->size);
}
greedy_joint_layers.resize(n_layers-1);
PP<RBMMixedLayer> ml = new RBMMixedLayer();
ml->sub_layers.resize(2);
ml->sub_layers[0] = layers[ i ];
ml->sub_layers[1] = greedy_target_layers[ i ];
ml->random_gen = random_gen;
ml->build();
greedy_joint_layers[i] = (RBMMixedLayer *)ml;
greedy_joint_connections.resize(n_layers-1);
PP<RBMMixedConnection> mc = new RBMMixedConnection();
mc->sub_connections.resize(1,2);
mc->sub_connections(0,0) = connections[i];
mc->sub_connections(0,1) = greedy_target_connections[i];
mc->build();
greedy_joint_connections[i] = (RBMMixedConnection *)mc;
if( !(greedy_target_connections[i]->random_gen) )
{
greedy_target_connections[i]->random_gen = random_gen;
greedy_target_connections[i]->forget();
}
if( !(greedy_target_layers[i]->random_gen) )
{
greedy_target_layers[i]->random_gen = random_gen;
greedy_target_layers[i]->forget();
}
}
if( use_corrupted_posDownVal != "none" )
{
if( greedy_target_layers.length() != 0 )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"use_corrupted_posDownVal not implemented for greedy_target_layers.");
if( online )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"use_corrupted_posDownVal not implemented for online.");
if( use_classification_cost )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"use_classification_cost not implemented for use_corrupted_posDownVal.");
if( background_gibbs_update_ratio != 0 )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"use_corrupted_posDownVal not implemented with background_gibbs_update_ratio!=0.");
if( batch_size != 1 || minibatch_hack )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"use_corrupted_posDownVal not implemented for batch_size != 1 or minibatch_hack.");
if( !partial_costs.isEmpty() )
PLERROR("DeepBeliefNet::build_layers_and_connections() - \n"
"use_corrupted_posDownVal not implemented for partial_costs.");
if( noise_type == "masking_noise" && fraction_of_masked_inputs > 0 )
{
expectation_indices[i].resize( layers[i]->size );
for( int j=0 ; j < expectation_indices[i].length() ; j++ )
expectation_indices[i][j] = j;
}
}
}
if( !(layers[n_layers-1]->random_gen) )
{
layers[n_layers-1]->random_gen = random_gen;
layers[n_layers-1]->forget();
}
int last_layer_size = layers[n_layers-1]->size;
PLASSERT_MSG(last_layer_size >= 0,
"Size of last layer must be non-negative");
activation_gradients[n_layers-1].resize(last_layer_size);
expectation_gradients[n_layers-1].resize(last_layer_size);
}

| string PLearn::DeepBeliefNet::classname | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 55 of file DeepBeliefNet.cc.
Referenced by train().

| void PLearn::DeepBeliefNet::computeClassifAndFinalCostsFromOutputs | ( | const Mat & | inputs, |
| const Mat & | outputs, | ||
| const Mat & | targets, | ||
| Mat & | costs | ||
| ) | const [virtual] |
Definition at line 3387 of file DeepBeliefNet.cc.
References PLearn::argmax(), class_cost_index, classification_cost, final_cost, final_cost_index, final_cost_values, PLearn::TVec< T >::isEmpty(), PLearn::TMat< T >::length(), n_classes, nll_cost_index, partial_costs, PLASSERT, PLERROR, PLearn::TMat< T >::subMat(), use_classification_cost, and PLearn::TMat< T >::width().
Referenced by computeOutputsAndCosts().
{
// Compute the costs from *already* computed output.
int nsamples = inputs.length();
PLASSERT( nsamples > 0 );
PLASSERT( targets.length() == nsamples );
PLASSERT( targets.width() == 1 );
PLASSERT( outputs.length() == nsamples );
PLASSERT( costs.length() == nsamples );
if( use_classification_cost )
{
Vec pcosts;
classification_cost->CostModule::fprop( outputs.subMat(0, 0, nsamples, n_classes),
targets, pcosts );
costs.subMat( 0, nll_cost_index, nsamples, 1) << pcosts;
for (int isample = 0; isample < nsamples; isample++ )
costs(isample,class_cost_index) =
(argmax(outputs(isample).subVec(0, n_classes)) == (int) round(targets(isample,0))) ? 0 : 1;
}
if( final_cost )
{
int init = use_classification_cost ? n_classes : 0;
final_cost->fprop( outputs.subMat(0, init, nsamples, outputs(0).size() - init ),
targets, final_cost_values );
costs.subMat(0, final_cost_index, nsamples, final_cost_values.width())
<< final_cost_values;
}
if( !partial_costs.isEmpty() )
PLERROR("cannot compute partial costs in DeepBeliefNet::computeCostsFromOutputs(Mat&, Mat&, Mat&, Mat&)"
"(expectations are not up to date in the batch version)");
}

| void PLearn::DeepBeliefNet::computeCostsFromOutputs | ( | const Vec & | input, |
| const Vec & | output, | ||
| const Vec & | target, | ||
| Vec & | costs | ||
| ) | const [virtual] |
Computes the costs from already computed output.
Implements PLearn::PLearner.
Definition at line 3288 of file DeepBeliefNet.cc.
References PLearn::argmax(), class_cost_index, classification_cost, PLearn::TVec< T >::clear(), cost_names, PLearn::TVec< T >::fill(), PLearn::fill_one_hot(), final_cost, final_cost_index, final_cost_value, greedy_target_layer_nlls_index, greedy_target_layers, i, PLearn::TVec< T >::isEmpty(), layers, PLearn::TVec< T >::length(), MISSING_VALUE, n_classes, n_layers, nll_cost_index, partial_costs, partial_costs_indices, reconstruct_layerwise, reconstruction_cost_index, reconstruction_costs, PLearn::TVec< T >::resize(), PLearn::TVec< T >::size(), PLearn::TVec< T >::subVec(), target_one_hot, and use_classification_cost.
{
// Compute the costs from *already* computed output.
costs.resize( cost_names.length() );
costs.fill( MISSING_VALUE );
// TO MAKE FOR CLEANER CODE INDEPENDENT OF ORDER OF CALLING THIS
// METHOD AND computeOutput, THIS SHOULD BE IN A REDEFINITION OF computeOutputAndCosts
if( use_classification_cost )
{
classification_cost->CostModule::fprop( output.subVec(0, n_classes),
target, costs[nll_cost_index] );
costs[class_cost_index] =
(argmax(output.subVec(0, n_classes)) == (int) round(target[0]))? 0 : 1;
}
if( final_cost )
{
int init = use_classification_cost ? n_classes : 0;
final_cost->fprop( output.subVec( init, output.size() - init ),
target, final_cost_value );
costs.subVec(final_cost_index, final_cost_value.length())
<< final_cost_value;
}
if( !partial_costs.isEmpty() )
{
Vec pcosts;
for( int i=0 ; i<n_layers-1 ; i++ )
// propagate into local cost associated to output of layer i+1
if( partial_costs[ i ] )
{
partial_costs[ i ]->fprop( layers[ i+1 ]->expectation,
target, pcosts);
costs.subVec(partial_costs_indices[i], pcosts.length())
<< pcosts;
}
}
if( !greedy_target_layers.isEmpty() )
{
target_one_hot.clear();
fill_one_hot( target_one_hot,
(int) round(target[0]), real(0.), real(1.) );
for( int i=0 ; i<n_layers-1 ; i++ )
if( greedy_target_layers[i] )
costs[greedy_target_layer_nlls_index+i] =
greedy_target_layers[i]->fpropNLL(target_one_hot);
else
costs[greedy_target_layer_nlls_index+i] = MISSING_VALUE;
}
if (reconstruct_layerwise)
costs.subVec(reconstruction_cost_index, reconstruction_costs.length())
<< reconstruction_costs;
}
Computes the output from the input.
We haven't computed the expectations of the top layer
Reconstruction error of the top layer
Reimplemented from PLearn::PLearner.
Definition at line 3115 of file DeepBeliefNet.cc.
References PLearn::TVec< T >::append(), c, classification_module, PLearn::TVec< T >::clear(), connections, final_cost, final_cost_input, final_module, greedy_target_connections, greedy_target_expectations, greedy_target_layers, i, i_output_layer, PLearn::TVec< T >::isEmpty(), layer_input, layers, PLearn::TVec< T >::length(), PLearn::multiplyScaledAdd(), n_classes, n_layers, outputsize(), partial_costs, reconstruct_layerwise, reconstruction_costs, PLearn::TVec< T >::resize(), PLearn::TVec< T >::toMat(), and use_classification_cost.
Referenced by computeOutputsAndCosts().
{
// Compute the output from the input.
output.resize(0);
// fprop
layers[0]->expectation << input;
if(reconstruct_layerwise)
reconstruction_costs[0]=0;
for( int i=0 ; i<n_layers-2 ; i++ )
{
if( greedy_target_layers.length() && greedy_target_layers[i] )
{
connections[i]->setAsDownInput( layers[i]->expectation );
layers[i+1]->getAllActivations( connections[i] );
greedy_target_layers[i]->activation.clear();
greedy_target_layers[i]->activation += greedy_target_layers[i]->bias;
for( int c=0; c<n_classes; c++ )
{
// Compute class free-energy
layers[i+1]->activation.toMat(layers[i+1]->size,1) += greedy_target_connections[i]->weights.column(c);
greedy_target_layers[i]->activation[c] -= layers[i+1]->freeEnergyContribution(layers[i+1]->activation);
// Compute class dependent expectation and store it
layers[i+1]->expectation_is_not_up_to_date();
layers[i+1]->computeExpectation();
greedy_target_expectations[i][c] << layers[i+1]->expectation;
// Remove class-dependent energy for next free-energy computations
layers[i+1]->activation.toMat(layers[i+1]->size,1) -= greedy_target_connections[i]->weights.column(c);
}
greedy_target_layers[i]->expectation_is_not_up_to_date();
greedy_target_layers[i]->computeExpectation();
// Computing next layer representation
layers[i+1]->expectation.clear();
Vec expectation = layers[i+1]->expectation;
for( int c=0; c<n_classes; c++ )
{
Vec expectation_c = greedy_target_expectations[i][c];
real p_c = greedy_target_layers[i]->expectation[c];
multiplyScaledAdd(expectation_c, real(1.), p_c, expectation);
}
}
else
{
connections[i]->setAsDownInput( layers[i]->expectation );
layers[i+1]->getAllActivations( connections[i] );
layers[i+1]->computeExpectation();
}
if( i_output_layer==i && (!use_classification_cost && !final_module))
{
output.resize(outputsize());
output << layers[ i ]->expectation;
}
if (reconstruct_layerwise)
{
layer_input.resize(layers[i]->size);
layer_input << layers[i]->expectation;
connections[i]->setAsUpInput(layers[i+1]->expectation);
layers[i]->getAllActivations(connections[i]);
real rc = reconstruction_costs[i+1] = layers[i]->fpropNLL( layer_input );
reconstruction_costs[0] += rc;
}
}
if( i_output_layer>=n_layers-2 && (!use_classification_cost && !final_module))
{
if(i_output_layer==n_layers-1)
{
connections[ n_layers-2 ]->setAsDownInput(layers[ n_layers-2 ]->expectation );
layers[ n_layers-1 ]->getAllActivations( connections[ n_layers-2 ] );
layers[ n_layers-1 ]->computeExpectation();
}
output.resize(outputsize());
output << layers[ i_output_layer ]->expectation;
}
if( use_classification_cost )
classification_module->fprop( layers[ n_layers-2 ]->expectation,
output );
if( final_cost || (!partial_costs.isEmpty() && partial_costs[n_layers-2] ))
{
if( greedy_target_layers.length() && greedy_target_layers[n_layers-2] )
{
connections[n_layers-2]->setAsDownInput( layers[n_layers-2]->expectation );
layers[n_layers-1]->getAllActivations( connections[n_layers-2] );
greedy_target_layers[n_layers-2]->activation.clear();
greedy_target_layers[n_layers-2]->activation +=
greedy_target_layers[n_layers-2]->bias;
for( int c=0; c<n_classes; c++ )
{
// Compute class free-energy
layers[n_layers-1]->activation.toMat(layers[n_layers-1]->size,1) +=
greedy_target_connections[n_layers-2]->weights.column(c);
greedy_target_layers[n_layers-2]->activation[c] -=
layers[n_layers-1]->freeEnergyContribution(layers[n_layers-1]->activation);
// Compute class dependent expectation and store it
layers[n_layers-1]->expectation_is_not_up_to_date();
layers[n_layers-1]->computeExpectation();
greedy_target_expectations[n_layers-2][c] << layers[n_layers-1]->expectation;
// Remove class-dependent energy for next free-energy computations
layers[n_layers-1]->activation.toMat(layers[n_layers-1]->size,1) -=
greedy_target_connections[n_layers-2]->weights.column(c);
}
greedy_target_layers[n_layers-2]->expectation_is_not_up_to_date();
greedy_target_layers[n_layers-2]->computeExpectation();
// Computing next layer representation
layers[n_layers-1]->expectation.clear();
Vec expectation = layers[n_layers-1]->expectation;
for( int c=0; c<n_classes; c++ )
{
Vec expectation_c = greedy_target_expectations[n_layers-2][c];
real p_c = greedy_target_layers[n_layers-2]->expectation[c];
multiplyScaledAdd(expectation_c,real(1.), p_c, expectation);
}
}
else
{
connections[ n_layers-2 ]->setAsDownInput(
layers[ n_layers-2 ]->expectation );
layers[ n_layers-1 ]->getAllActivations( connections[ n_layers-2 ] );
layers[ n_layers-1 ]->computeExpectation();
}
if( final_module )
{
final_module->fprop( layers[ n_layers-1 ]->expectation,
final_cost_input );
output.append( final_cost_input );
}
else
{
output.append( layers[ n_layers-1 ]->expectation );
}
if (reconstruct_layerwise)
{
layer_input.resize(layers[n_layers-2]->size);
layer_input << layers[n_layers-2]->expectation;
connections[n_layers-2]->setAsUpInput(layers[n_layers-1]->expectation);
layers[n_layers-2]->getAllActivations(connections[n_layers-2]);
real rc = reconstruction_costs[n_layers-1] = layers[n_layers-2]->fpropNLL( layer_input );
reconstruction_costs[0] += rc;
}
}
if(!use_classification_cost && !final_module)
{
if (reconstruct_layerwise)
{
layer_input.resize(layers[n_layers-2]->size);
layer_input << layers[n_layers-2]->expectation;
connections[n_layers-2]->setAsUpInput(layers[n_layers-1]->expectation);
layers[n_layers-2]->getAllActivations(connections[n_layers-2]);
real rc = reconstruction_costs[n_layers-1] = layers[n_layers-2]->fpropNLL( layer_input );
reconstruction_costs[0] += rc;
}
}
}

| void PLearn::DeepBeliefNet::computeOutputsAndCosts | ( | const Mat & | inputs, |
| const Mat & | targets, | ||
| Mat & | outputs, | ||
| Mat & | costs | ||
| ) | const [virtual] |
This function is usefull when the NLL CostModule AND/OR the final_cost Module are more efficient with batch computation (or need to be computed on a bunch of examples, as LayerCostModule)
Reimplemented from PLearn::PLearner.
Definition at line 3353 of file DeepBeliefNet.cc.
References computeClassifAndFinalCostsFromOutputs(), computeOutput(), cost_names, PLearn::TMat< T >::fill(), i, PLearn::TVec< T >::isEmpty(), layers, PLearn::TVec< T >::length(), PLearn::TMat< T >::length(), MISSING_VALUE, n_layers, outputsize(), partial_costs, partial_costs_indices, PLASSERT, reconstruct_layerwise, reconstruction_cost_index, reconstruction_costs, and PLearn::TMat< T >::resize().
{
int nsamples = inputs.length();
PLASSERT( targets.length() == nsamples );
outputs.resize( nsamples, outputsize() );
costs.resize( nsamples, cost_names.length() );
costs.fill( MISSING_VALUE );
for (int isample = 0; isample < nsamples; isample++ )
{
Vec in_i = inputs(isample);
Vec out_i = outputs(isample);
computeOutput(in_i, out_i);
if( !partial_costs.isEmpty() )
{
Vec pcosts;
for( int i=0 ; i<n_layers-1 ; i++ )
// propagate into local cost associated to output of layer i+1
if( partial_costs[ i ] )
{
partial_costs[ i ]->fprop( layers[ i+1 ]->expectation,
targets(isample), pcosts);
costs(isample).subVec(partial_costs_indices[i], pcosts.length())
<< pcosts;
}
}
if (reconstruct_layerwise)
costs(isample).subVec(reconstruction_cost_index, reconstruction_costs.length())
<< reconstruction_costs;
}
computeClassifAndFinalCostsFromOutputs(inputs, outputs, targets, costs);
}
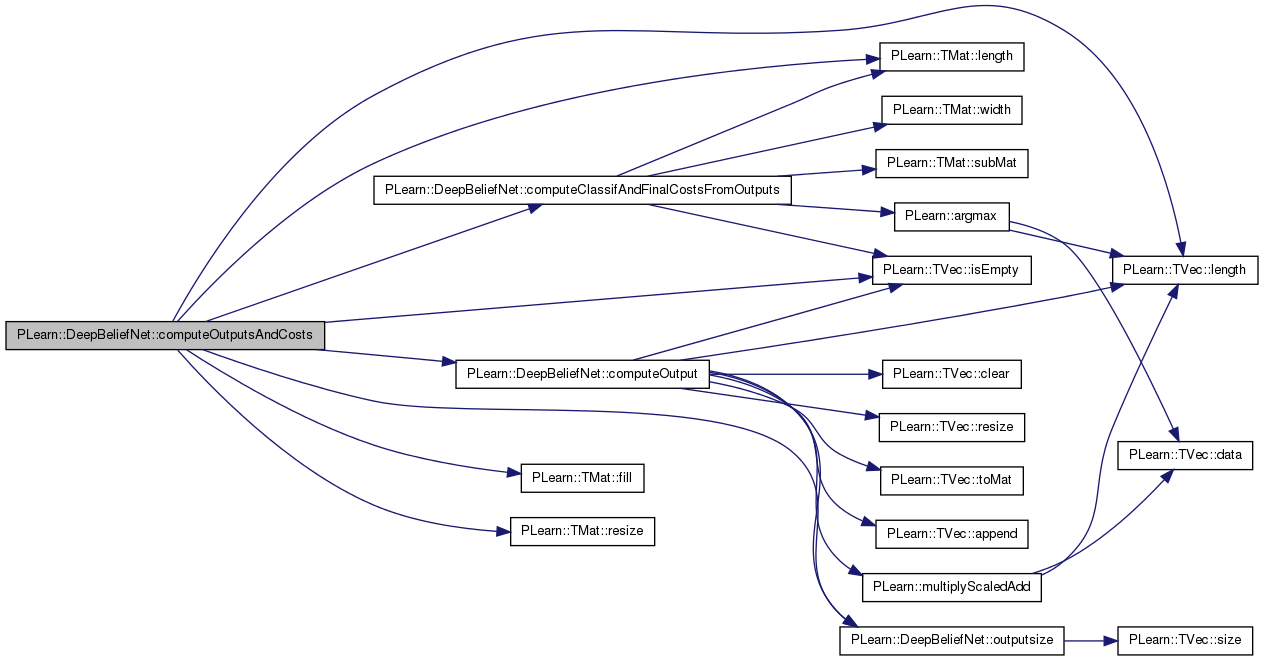
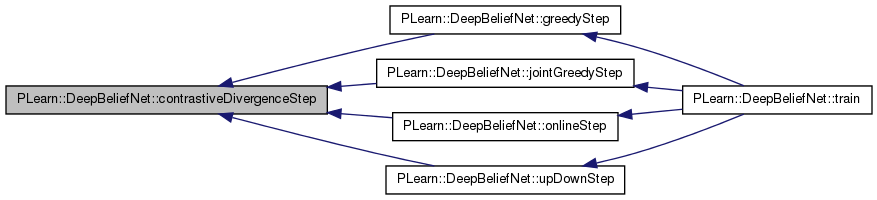
| void PLearn::DeepBeliefNet::contrastiveDivergenceStep | ( | const PP< RBMLayer > & | down_layer, |
| const PP< RBMConnection > & | connection, | ||
| const PP< RBMLayer > & | up_layer, | ||
| int | layer_index, | ||
| bool | nofprop = false |
||
| ) |
Perform a step of contrastive divergence, assuming that down_layer->expectation(s) is set.
Definition at line 2802 of file DeepBeliefNet.cc.
References background_gibbs_update_ratio, cd_neg_down_vals, cd_neg_up_vals, corrupt_input(), corrupted_pos_down_val, gibbs_down_state, initialize_gibbs_chain, mean_field_contrastive_divergence_ratio, mf_cd_neg_down_val, mf_cd_neg_down_vals, mf_cd_neg_up_val, mf_cd_neg_up_vals, minibatch_hack, minibatch_size, pos_down_val, pos_down_vals, pos_up_val, pos_up_vals, PLearn::TMat< T >::resize(), PLearn::TVec< T >::resize(), use_corrupted_posDownVal, and use_sample_for_up_layer.
Referenced by greedyStep(), jointGreedyStep(), onlineStep(), and upDownStep().
{
bool mbatch = minibatch_size > 1 || minibatch_hack;
// positive phase
if (!nofprop)
{
if (mbatch) {
connection->setAsDownInputs( down_layer->getExpectations() );
up_layer->getAllActivations( connection, 0, true );
up_layer->computeExpectations();
} else {
if( use_corrupted_posDownVal == "for_cd_fprop" )
{
corrupted_pos_down_val.resize( down_layer->size );
corrupt_input( down_layer->expectation, corrupted_pos_down_val, layer_index );
connection->setAsDownInput( corrupted_pos_down_val );
}
else
connection->setAsDownInput( down_layer->expectation );
up_layer->getAllActivations( connection );
up_layer->computeExpectation();
}
}
if (mbatch)
{
// accumulate positive stats using the expectation
// we deep-copy because the value will change during negative phase
pos_down_vals.resize(minibatch_size, down_layer->size);
pos_up_vals.resize(minibatch_size, up_layer->size);
pos_down_vals << down_layer->getExpectations();
pos_up_vals << up_layer->getExpectations();
up_layer->generateSamples();
// down propagation, starting from a sample of up_layer
if (background_gibbs_update_ratio<1)
// then do some contrastive divergence, o/w only background Gibbs
{
Mat neg_down_vals;
Mat neg_up_vals;
if( mean_field_contrastive_divergence_ratio > 0 )
{
mf_cd_neg_down_vals.resize(minibatch_size, down_layer->size);
mf_cd_neg_up_vals.resize(minibatch_size, up_layer->size);
connection->setAsUpInputs( up_layer->getExpectations() );
down_layer->getAllActivations( connection, 0, true );
down_layer->computeExpectations();
// negative phase
connection->setAsDownInputs( down_layer->getExpectations() );
up_layer->getAllActivations( connection, 0, mbatch );
up_layer->computeExpectations();
mf_cd_neg_down_vals << down_layer->getExpectations();
mf_cd_neg_up_vals << up_layer->getExpectations();
}
if( mean_field_contrastive_divergence_ratio < 1 )
{
if( use_sample_for_up_layer )
pos_up_vals << up_layer->samples;
connection->setAsUpInputs( up_layer->samples );
down_layer->getAllActivations( connection, 0, true );
down_layer->computeExpectations();
down_layer->generateSamples();
// negative phase
connection->setAsDownInputs( down_layer->samples );
up_layer->getAllActivations( connection, 0, mbatch );
up_layer->computeExpectations();
neg_down_vals = down_layer->samples;
if( use_sample_for_up_layer)
{
up_layer->generateSamples();
neg_up_vals = up_layer->samples;
}
else
neg_up_vals = up_layer->getExpectations();
}
if (background_gibbs_update_ratio==0)
// update here only if there is ONLY contrastive divergence
{
if( mean_field_contrastive_divergence_ratio < 1 )
{
real lr_dl = down_layer->learning_rate;
real lr_ul = up_layer->learning_rate;
real lr_c = connection->learning_rate;
down_layer->setLearningRate(lr_dl * (1-mean_field_contrastive_divergence_ratio));
up_layer->setLearningRate(lr_ul * (1-mean_field_contrastive_divergence_ratio));
connection->setLearningRate(lr_c * (1-mean_field_contrastive_divergence_ratio));
down_layer->update( pos_down_vals, neg_down_vals );
connection->update( pos_down_vals, pos_up_vals,
neg_down_vals, neg_up_vals );
up_layer->update( pos_up_vals, neg_up_vals );
down_layer->setLearningRate(lr_dl);
up_layer->setLearningRate(lr_ul);
connection->setLearningRate(lr_c);
}
if( mean_field_contrastive_divergence_ratio > 0 )
{
real lr_dl = down_layer->learning_rate;
real lr_ul = up_layer->learning_rate;
real lr_c = connection->learning_rate;
down_layer->setLearningRate(lr_dl * mean_field_contrastive_divergence_ratio);
up_layer->setLearningRate(lr_ul * mean_field_contrastive_divergence_ratio);
connection->setLearningRate(lr_c * mean_field_contrastive_divergence_ratio);
down_layer->update( pos_down_vals, mf_cd_neg_down_vals );
connection->update( pos_down_vals, pos_up_vals,
mf_cd_neg_down_vals, mf_cd_neg_up_vals );
up_layer->update( pos_up_vals, mf_cd_neg_up_vals );
down_layer->setLearningRate(lr_dl);
up_layer->setLearningRate(lr_ul);
connection->setLearningRate(lr_c);
}
}
else
{
connection->accumulatePosStats(pos_down_vals,pos_up_vals);
cd_neg_down_vals.resize(minibatch_size, down_layer->size);
cd_neg_up_vals.resize(minibatch_size, up_layer->size);
cd_neg_down_vals << neg_down_vals;
cd_neg_up_vals << neg_up_vals;
}
}
//
if (background_gibbs_update_ratio>0)
{
Mat down_state = gibbs_down_state[layer_index];
if (initialize_gibbs_chain) // initializing or re-initializing the chain
{
if (background_gibbs_update_ratio==1) // if <1 just use the CD state
{
up_layer->generateSamples();
connection->setAsUpInputs(up_layer->samples);
down_layer->getAllActivations(connection, 0, true);
down_layer->generateSamples();
down_state << down_layer->samples;
}
initialize_gibbs_chain=false;
}
// sample up state given down state
connection->setAsDownInputs(down_state);
up_layer->getAllActivations(connection, 0, true);
up_layer->generateSamples();
// sample down state given up state, to prepare for next time
connection->setAsUpInputs(up_layer->samples);
down_layer->getAllActivations(connection, 0, true);
down_layer->generateSamples();
// update using the down_state and up_layer->expectations for moving average in negative phase
// (and optionally
if (background_gibbs_update_ratio<1)
{
down_layer->updateCDandGibbs(pos_down_vals,cd_neg_down_vals,
down_state,
background_gibbs_update_ratio);
connection->updateCDandGibbs(pos_down_vals,pos_up_vals,
cd_neg_down_vals, cd_neg_up_vals,
down_state,
up_layer->getExpectations(),
background_gibbs_update_ratio);
up_layer->updateCDandGibbs(pos_up_vals,cd_neg_up_vals,
up_layer->getExpectations(),
background_gibbs_update_ratio);
}
else
{
down_layer->updateGibbs(pos_down_vals,down_state);
connection->updateGibbs(pos_down_vals,pos_up_vals,down_state,
up_layer->getExpectations());
up_layer->updateGibbs(pos_up_vals,up_layer->getExpectations());
}
// Save Gibbs chain's state.
down_state << down_layer->samples;
}
} else {
// accumulate positive stats using the expectation
// we deep-copy because the value will change during negative phase
pos_down_val.resize( down_layer->size );
pos_up_val.resize( up_layer->size );
Vec neg_down_val;
Vec neg_up_val;
pos_down_val << down_layer->expectation;
pos_up_val << up_layer->expectation;
up_layer->generateSample();
// negative phase
// down propagation, starting from a sample of up_layer
if( mean_field_contrastive_divergence_ratio > 0 )
{
connection->setAsUpInput( up_layer->expectation );
down_layer->getAllActivations( connection );
down_layer->computeExpectation();
connection->setAsDownInput( down_layer->expectation );
up_layer->getAllActivations( connection, 0, mbatch );
up_layer->computeExpectation();
mf_cd_neg_down_val.resize( down_layer->size );
mf_cd_neg_up_val.resize( up_layer->size );
mf_cd_neg_down_val << down_layer->expectation;
mf_cd_neg_up_val << up_layer->expectation;
}
if( mean_field_contrastive_divergence_ratio < 1 )
{
if( use_sample_for_up_layer )
pos_up_val << up_layer->sample;
connection->setAsUpInput( up_layer->sample );
down_layer->getAllActivations( connection );
down_layer->computeExpectation();
down_layer->generateSample();
connection->setAsDownInput( down_layer->sample );
up_layer->getAllActivations( connection, 0, mbatch );
up_layer->computeExpectation();
neg_down_val = down_layer->sample;
if( use_sample_for_up_layer )
{
up_layer->generateSample();
neg_up_val = up_layer->sample;
}
else
neg_up_val = up_layer->expectation;
}
// update
if( mean_field_contrastive_divergence_ratio < 1 )
{
real lr_dl = down_layer->learning_rate;
real lr_ul = up_layer->learning_rate;
real lr_c = connection->learning_rate;
down_layer->setLearningRate(lr_dl * (1-mean_field_contrastive_divergence_ratio));
up_layer->setLearningRate(lr_ul * (1-mean_field_contrastive_divergence_ratio));
connection->setLearningRate(lr_c * (1-mean_field_contrastive_divergence_ratio));
if( use_corrupted_posDownVal == "for_cd_update" )
{
corrupted_pos_down_val.resize( down_layer->size );
corrupt_input( pos_down_val, corrupted_pos_down_val, layer_index );
down_layer->update( corrupted_pos_down_val, neg_down_val );
connection->update( corrupted_pos_down_val, pos_up_val,
neg_down_val, neg_up_val );
}
else
{
down_layer->update( pos_down_val, neg_down_val );
connection->update( pos_down_val, pos_up_val,
neg_down_val, neg_up_val );
}
up_layer->update( pos_up_val, neg_up_val );
down_layer->setLearningRate(lr_dl);
up_layer->setLearningRate(lr_ul);
connection->setLearningRate(lr_c);
}
if( mean_field_contrastive_divergence_ratio > 0 )
{
real lr_dl = down_layer->learning_rate;
real lr_ul = up_layer->learning_rate;
real lr_c = connection->learning_rate;
down_layer->setLearningRate(lr_dl * mean_field_contrastive_divergence_ratio);
up_layer->setLearningRate(lr_ul * mean_field_contrastive_divergence_ratio);
connection->setLearningRate(lr_c * mean_field_contrastive_divergence_ratio);
if( use_corrupted_posDownVal == "for_cd_update" )
{
corrupted_pos_down_val.resize( down_layer->size );
corrupt_input( pos_down_val, corrupted_pos_down_val, layer_index );
down_layer->update( corrupted_pos_down_val, mf_cd_neg_down_val );
connection->update( corrupted_pos_down_val, pos_up_val,
mf_cd_neg_down_val, mf_cd_neg_up_val );
}
else
{
down_layer->update( pos_down_val, mf_cd_neg_down_val );
connection->update( pos_down_val, pos_up_val,
mf_cd_neg_down_val, mf_cd_neg_up_val );
}
up_layer->update( pos_up_val, mf_cd_neg_up_val );
down_layer->setLearningRate(lr_dl);
up_layer->setLearningRate(lr_ul);
connection->setLearningRate(lr_c);
}
}
}

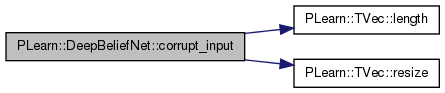
| void PLearn::DeepBeliefNet::corrupt_input | ( | const Vec & | input, |
| Vec & | corrupted_input, | ||
| int | layer | ||
| ) | [private] |
Definition at line 3430 of file DeepBeliefNet.cc.
References expectation_indices, fraction_of_masked_inputs, j, PLearn::TVec< T >::length(), mask_with_pepper_salt, noise_type, PLERROR, prob_salt_noise, PLearn::PLearner::random_gen, and PLearn::TVec< T >::resize().
Referenced by contrastiveDivergenceStep(), and greedyStep().
{
corrupted_input.resize(input.length());
if( noise_type == "masking_noise" )
{
corrupted_input << input;
if( fraction_of_masked_inputs != 0 )
{
random_gen->shuffleElements(expectation_indices[layer]);
if( mask_with_pepper_salt )
for( int j=0 ; j < round(fraction_of_masked_inputs*input.length()) ; j++)
corrupted_input[ expectation_indices[layer][j] ] = random_gen->binomial_sample(prob_salt_noise);
else
for( int j=0 ; j < round(fraction_of_masked_inputs*input.length()) ; j++)
corrupted_input[ expectation_indices[layer][j] ] = 0;
}
}
/* else if( noise_type == "binary_sampling" )
{
for( int i=0; i<corrupted_input.length(); i++ )
corrupted_input[i] = random_gen->binomial_sample((input[i]-0.5)*binary_sampling_noise_parameter+0.5);
}
else if( noise_type == "gaussian" )
{
for( int i=0; i<corrupted_input.length(); i++ )
corrupted_input[i] = input[i] +
random_gen->gaussian_01() * gaussian_std;
}
else
PLERROR("In StackedAutoassociatorsNet::corrupt_input(): "
"missing_data_method %s not valid with noise_type %s",
missing_data_method.c_str(), noise_type.c_str());
}*/
else if( noise_type == "none" )
corrupted_input << input;
else
PLERROR("In DeepBeliefNet::corrupt_input(): noise_type %s not valid", noise_type.c_str());
}

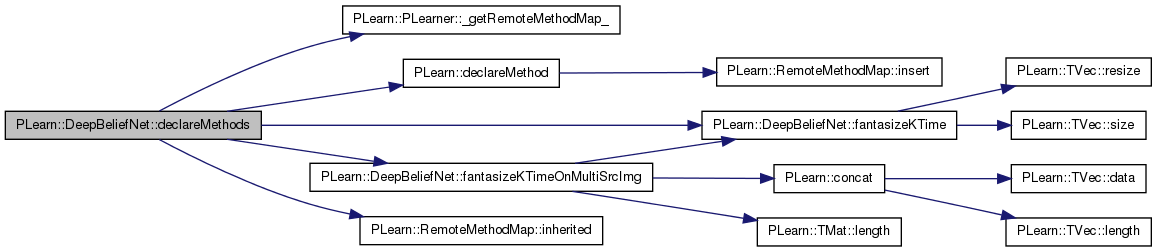
| void PLearn::DeepBeliefNet::declareMethods | ( | RemoteMethodMap & | rmm | ) | [static, protected] |
Declare the methods that are remote-callable.
Reimplemented from PLearn::PLearner.
Definition at line 105 of file DeepBeliefNet.cc.
References PLearn::PLearner::_getRemoteMethodMap_(), PLearn::declareMethod(), fantasizeKTime(), fantasizeKTimeOnMultiSrcImg(), and PLearn::RemoteMethodMap::inherited().
{
// Insert a backpointer to remote methods; note that this is different from declareOptions().
rmm.inherited(inherited::_getRemoteMethodMap_());
declareMethod(
rmm, "fantasizeKTime",
&DeepBeliefNet::fantasizeKTime,
(BodyDoc("On a trained learner, computes a codage-decodage (fantasize) through a specified number of hidden layer."),
ArgDoc ("kTime", "Number of time we want to fantasize. \n"
"Next input image will again be the source Image (if alwaysFromSrcImg is True) \n"
"or next input image will be the last fantasize image (if alwaysFromSrcImg is False), and so on for kTime.)"),
ArgDoc ("srcImg", "Source image vector (should have same width as raws layer)"),
ArgDoc ("sampling", "Vector of bool indicating whether or not a sampling will be done for each hidden layer\n"
"during decodage. Its width indicates how many hidden layer will be used.)\n"
" (should have same width as maskNoiseFractOrProb)\n"
"smaller element of the vector correspond to lower layer"),
ArgDoc ("alwaysFromSrcImg", "Booleen indicating whether each encode-decode \n"
"steps are done from the source image (sets to True) or \n"
"if the next input image is the last fantasize image (sets to False). "),
RetDoc ("Fantasize images obtained for each kTime.")));
declareMethod(
rmm, "fantasizeKTimeOnMultiSrcImg",
&DeepBeliefNet::fantasizeKTimeOnMultiSrcImg,
(BodyDoc("Call the 'fantasizeKTime' function for each source images found in the matrix 'srcImg'."),
ArgDoc ("kTime", "Number of time we want to fantasize for each source images. \n"
"Next input image will again be the source Image (if alwaysFromSrcImg is True) \n"
"or next input image will be the last fantasize image (if alwaysFromSrcImg is False), and so on for kTime.)"),
ArgDoc ("srcImg", "Source images matrix (should have same width as raws layer)"),
ArgDoc ("sampling", "Vector of bool indicating whether or not a sampling will be done for each hidden layer\n"
"during decodage. Its width indicates how many hidden layer will be used.)\n"
" (should have same width as maskNoiseFractOrProb)\n"
"smaller element of the vector correspond to lower layer"),
ArgDoc ("alwaysFromSrcImg", "Booleen indicating whether each encode-decode \n"
"steps are done from the source image (sets to True) or \n"
"if the next input image is the preceding fantasize image obtained (sets to False). "),
RetDoc ("For each source images, fantasize images obtained for each kTime.")));
}
| void PLearn::DeepBeliefNet::declareOptions | ( | OptionList & | ol | ) | [static, protected] |
Declares the class options.
Reimplemented from PLearn::PLearner.
Definition at line 150 of file DeepBeliefNet.cc.
References background_gibbs_update_ratio, batch_size, PLearn::OptionBase::buildoption, cd_decrease_ct, cd_learning_rate, classification_cost, classification_module, connections, cumulative_testing_time, cumulative_training_time, PLearn::declareOption(), PLearn::PLearner::declareOptions(), final_cost, final_module, fraction_of_masked_inputs, generative_connections, gibbs_chain_reinit_freq, gibbs_down_state, grad_decrease_ct, grad_learning_rate, greedy_target_connections, greedy_target_layers, i_output_layer, joint_layer, layers, learnerExpdir, PLearn::OptionBase::learntoption, mask_with_pepper_salt, mean_field_contrastive_divergence_ratio, minibatch_size, n_classes, n_layers, noise_type, PLearn::OptionBase::nosave, online, partial_costs, prob_salt_noise, reconstruct_layerwise, save_learner_before_fine_tuning, top_layer_joint_cd, train_stats_window, training_schedule, up_down_decrease_ct, up_down_learning_rate, up_down_nstages, up_down_stage, use_classification_cost, use_corrupted_posDownVal, and use_sample_for_up_layer.
{
declareOption(ol, "cd_learning_rate", &DeepBeliefNet::cd_learning_rate,
OptionBase::buildoption,
"The learning rate used during contrastive divergence"
" learning");
declareOption(ol, "cd_decrease_ct", &DeepBeliefNet::cd_decrease_ct,
OptionBase::buildoption,
"The decrease constant of the learning rate used during"
" contrastive divergence");
declareOption(ol, "up_down_learning_rate",
&DeepBeliefNet::up_down_learning_rate,
OptionBase::buildoption,
"The learning rate used in the up-down algorithm during the\n"
"unsupervised fine tuning gradient descent.\n");
declareOption(ol, "up_down_decrease_ct", &DeepBeliefNet::up_down_decrease_ct,
OptionBase::buildoption,
"The decrease constant of the learning rate used in the\n"
"up-down algorithm during the unsupervised fine tuning\n"
"gradient descent.\n");
declareOption(ol, "grad_learning_rate", &DeepBeliefNet::grad_learning_rate,
OptionBase::buildoption,
"The learning rate used during gradient descent");
declareOption(ol, "grad_decrease_ct", &DeepBeliefNet::grad_decrease_ct,
OptionBase::buildoption,
"The decrease constant of the learning rate used during"
" gradient descent");
declareOption(ol, "batch_size", &DeepBeliefNet::batch_size,
OptionBase::buildoption,
"Training batch size (1=stochastic learning, 0=full batch learning).");
/* NOT IMPLEMENTED YET
declareOption(ol, "grad_weight_decay", &DeepBeliefNet::grad_weight_decay,
OptionBase::buildoption,
"The weight decay used during the gradient descent");
*/
declareOption(ol, "n_classes", &DeepBeliefNet::n_classes,
OptionBase::buildoption,
"Number of classes in the training set:\n"
" - 0 means we are doing regression,\n"
" - 1 means we have two classes, but only one output,\n"
" - 2 means we also have two classes, but two outputs"
" summing to 1,\n"
" - >2 is the usual multiclass case.\n"
);
declareOption(ol, "training_schedule", &DeepBeliefNet::training_schedule,
OptionBase::buildoption,
"Number of examples to use during each phase of learning:\n"
"first the greedy phases, and then the fine-tuning phase.\n"
"However, the learning will stop as soon as we reach nstages.\n"
"For example for 2 hidden layers, with 1000 examples in each\n"
"greedy phase, and 500 in the fine-tuning phase, this option\n"
"should be [1000 1000 500], and nstages should be at least 2500.\n"
"When online = true, this vector is ignored and should be empty.\n");
declareOption(ol, "up_down_nstages", &DeepBeliefNet::up_down_nstages,
OptionBase::buildoption,
"Number of samples to use for unsupervised fine-tuning\n"
"with the up-down algorithm. The unsupervised fine-tuning will\n"
"be executed between the greedy layer-wise learning and the\n"
"supervised fine-tuning. The up-down algorithm only works for\n"
"RBMMatrixConnection connections.\n");
declareOption(ol, "use_classification_cost",
&DeepBeliefNet::use_classification_cost,
OptionBase::buildoption,
"Put the class target as an extra input of the top-level RBM\n"
"and compute and maximize conditional class probability in that\n"
"top layer (probability of the correct class given the other input\n"
"of the top-level RBM, which is the output of the rest of the network.\n");
declareOption(ol, "reconstruct_layerwise",
&DeepBeliefNet::reconstruct_layerwise,
OptionBase::buildoption,
"Compute reconstruction error of each layer as an auto-encoder.\n"
"This is done using cross-entropy between actual and reconstructed.\n"
"This option automatically adds the following cost names:\n"
" layerwise_reconstruction_error (sum over all layers)\n"
" layer0.reconstruction_error (only layers[0])\n"
" layer1.reconstruction_error (only layers[1])\n"
" etc.\n");
declareOption(ol, "layers", &DeepBeliefNet::layers,
OptionBase::buildoption,
"The layers of units in the network (including the input layer).");
declareOption(ol, "i_output_layer", &DeepBeliefNet::i_output_layer,
OptionBase::buildoption,
"The index of the layers from which you want to compute output"
"when there is NO final_module NEITHER final_cost."
"If -1, then the outputs (with this setting) will be"
"the expectations of the last layer.");
declareOption(ol, "connections", &DeepBeliefNet::connections,
OptionBase::buildoption,
"The weights of the connections between the layers");
declareOption(ol, "greedy_target_layers", &DeepBeliefNet::greedy_target_layers,
OptionBase::buildoption,
"Optional target layers for greedy layer-wise pretraining");
declareOption(ol, "greedy_target_connections", &DeepBeliefNet::greedy_target_connections,
OptionBase::buildoption,
"Optional target matrix connections for greedy layer-wise pretraining");
declareOption(ol, "learnerExpdir",
&DeepBeliefNet::learnerExpdir,
OptionBase::buildoption,
"Experiment directory where the learner will be save\n"
"if save_learner_before_fine_tuning is true."
);
declareOption(ol, "save_learner_before_fine_tuning",
&DeepBeliefNet::save_learner_before_fine_tuning,
OptionBase::buildoption,
"Saves the learner before the supervised fine-tuning."
);
declareOption(ol, "classification_module",
&DeepBeliefNet::classification_module,
OptionBase::learntoption,
"The module computing the class probabilities (if"
" use_classification_cost)\n"
);
declareOption(ol, "classification_cost",
&DeepBeliefNet::classification_cost,
OptionBase::nosave,
"The module computing the classification cost function (NLL)"
" on top\n"
"of classification_module.\n"
);
declareOption(ol, "joint_layer", &DeepBeliefNet::joint_layer,
OptionBase::nosave,
"Concatenation of layers[n_layers-2] and the target layer\n"
"(that is inside classification_module), if"
" use_classification_cost.\n"
);
declareOption(ol, "final_module", &DeepBeliefNet::final_module,
OptionBase::buildoption,
"Optional module that takes as input the output of the last"
" layer\n"
"layers[n_layers-1), and its output is fed to final_cost,"
" and\n"
"concatenated with the one of classification_cost (if"
" present)\n"
"as output of the learner.\n"
"If it is not provided, then the last layer will directly be"
" put as\n"
"input of final_cost.\n"
);
declareOption(ol, "final_cost", &DeepBeliefNet::final_cost,
OptionBase::buildoption,
"The cost function to be applied on top of the DBN (or of\n"
"final_module if provided). Its gradients will be"
" backpropagated\n"
"to final_module, then combined with the one of"
" classification_cost and\n"
"backpropagated to the layers.\n"
);
declareOption(ol, "partial_costs", &DeepBeliefNet::partial_costs,
OptionBase::buildoption,
"The different cost functions to be applied on top of each"
" layer\n"
"(except the first one) of the RBM. These costs are not\n"
"back-propagated to previous layers.\n");
declareOption(ol, "use_sample_for_up_layer", &DeepBeliefNet::use_sample_for_up_layer,
OptionBase::buildoption,
"Indication that the update of the top layer during CD uses\n"
"a sample, not the expectation.\n");
declareOption(ol, "use_corrupted_posDownVal",
&DeepBeliefNet::use_corrupted_posDownVal,
OptionBase::buildoption,
"Indicates whether we will use a corrupted version of the\n"
"positive down value during the CD step.\n"
"Choose among:\n"
" - \"for_cd_fprop\"\n"
" - \"for_cd_update\"\n"
" - \"none\"\n");
declareOption(ol, "noise_type",
&DeepBeliefNet::noise_type,
OptionBase::buildoption,
"Type of noise that corrupts the pos_down_val. "
"Choose among:\n"
" - \"masking_noise\"\n"
" - \"none\"\n");
declareOption(ol, "fraction_of_masked_inputs",
&DeepBeliefNet::fraction_of_masked_inputs,
OptionBase::buildoption,
"Fraction of the pos_down_val components which\n"
"will be masked.\n");
declareOption(ol, "mask_with_pepper_salt",
&DeepBeliefNet::mask_with_pepper_salt,
OptionBase::buildoption,
"Indication that inputs should be masked with "
"0 or 1 according to prob_salt_noise.\n");
declareOption(ol, "prob_salt_noise",
&DeepBeliefNet::prob_salt_noise,
OptionBase::buildoption,
"Probability that we mask the input by 1 instead of 0.\n");
declareOption(ol, "online", &DeepBeliefNet::online,
OptionBase::buildoption,
"If true then all unsupervised training stages (as well as\n"
"the fine-tuning stage) are done simultaneously.\n");
declareOption(ol, "background_gibbs_update_ratio", &DeepBeliefNet::background_gibbs_update_ratio,
OptionBase::buildoption,
"Coefficient between 0 and 1. If non-zero, run a background Gibbs chain and use\n"
"the visible-hidden statistics to contribute in the negative phase update\n"
"(in proportion background_gibbs_update_ratio wrt the contrastive divergence\n"
"negative phase statistics). If = 1, then do not perform any contrastive\n"
"divergence negative phase (use only the Gibbs chain statistics).\n");
declareOption(ol, "gibbs_chain_reinit_freq",
&DeepBeliefNet::gibbs_chain_reinit_freq,
OptionBase::buildoption,
"After how many training examples to re-initialize the Gibbs chains.\n"
"If == INT_MAX, the default value of this option, then NEVER\n"
"re-initialize except at the beginning, when stage==0.\n");
declareOption(ol, "mean_field_contrastive_divergence_ratio",
&DeepBeliefNet::mean_field_contrastive_divergence_ratio,
OptionBase::buildoption,
"Coefficient between 0 and 1. 0 means CD-1 update only and\n"
"1 means MF-CD only. Values in between means a weighted\n"
"combination of both.\n");
declareOption(ol, "train_stats_window",
&DeepBeliefNet::train_stats_window,
OptionBase::buildoption,
"The number of samples to use to compute training stats.\n"
"-1 (default) means the number of training samples.\n");
declareOption(ol, "top_layer_joint_cd", &DeepBeliefNet::top_layer_joint_cd,
OptionBase::buildoption,
"Wether we do a step of joint contrastive divergence on"
" top-layer.\n"
"Only used if online for the moment.\n");
declareOption(ol, "n_layers", &DeepBeliefNet::n_layers,
OptionBase::learntoption,
"Number of layers");
declareOption(ol, "minibatch_size", &DeepBeliefNet::minibatch_size,
OptionBase::learntoption,
"Actual size of a mini-batch (size of the training set if"
" batch_size==1).");
declareOption(ol, "gibbs_down_state", &DeepBeliefNet::gibbs_down_state,
OptionBase::learntoption,
"State of visible units of RBMs at each layer in background"
" Gibbs chain.");
declareOption(ol, "cumulative_training_time",
&DeepBeliefNet::cumulative_training_time,
OptionBase::learntoption | OptionBase::nosave,
"Cumulative training time since age=0, in seconds.\n");
declareOption(ol, "cumulative_testing_time",
&DeepBeliefNet::cumulative_testing_time,
OptionBase::learntoption | OptionBase::nosave,
"Cumulative testing time since age=0, in seconds.\n");
declareOption(ol, "up_down_stage", &DeepBeliefNet::up_down_stage,
OptionBase::learntoption,
"Number of samples visited so far during unsupervised\n"
"fine-tuning.\n");
declareOption(ol, "generative_connections",
&DeepBeliefNet::generative_connections,
OptionBase::learntoption,
"The untied generative weights of the connections"
"between the layers\n"
"for the up-down algorithm.\n");
// Now call the parent class' declareOptions
inherited::declareOptions(ol);
}

| static const PPath& PLearn::DeepBeliefNet::declaringFile | ( | ) | [inline, static] |
| DeepBeliefNet * PLearn::DeepBeliefNet::deepCopy | ( | CopiesMap & | copies | ) | const [virtual] |
Reimplemented from PLearn::PLearner.
Definition at line 55 of file DeepBeliefNet.cc.
Referenced by train().

| TVec< Vec > PLearn::DeepBeliefNet::fantasizeKTime | ( | const int | KTime, |
| const Vec & | srcImg, | ||
| const Vec & | sample, | ||
| bool | alwaysFromSrcImg | ||
| ) | [private] |
Definition at line 3592 of file DeepBeliefNet.cc.
References connections, i, j, layers, n_layers, PLERROR, PLearn::PLearner::random_gen, PLearn::TVec< T >::resize(), and PLearn::TVec< T >::size().
Referenced by declareMethods(), and fantasizeKTimeOnMultiSrcImg().
{
if(sample.size() > n_layers-1)
PLERROR("In DeepBeliefNet::fantasize():"
" Size of sample (%i) should be <= "
"number of hidden layer (%i).",sample.size(), n_layers-1);
int n_hlayers_used = sample.size();
TVec<Vec> fantaImagesObtained(KTime+1);
fantaImagesObtained[0].resize(srcImg.size());
fantaImagesObtained[0] << srcImg;
layers[0]->setExpectation(srcImg);
for( int k=0 ; k<KTime ; k++ )
{
fantaImagesObtained[k+1].resize(srcImg.size());
for( int i=0 ; i<n_hlayers_used; i++ )
{
connections[i]->setAsDownInput( layers[i]->expectation );
layers[i+1]->getAllActivations( connections[i], 0, false );
layers[i+1]->computeExpectation();
}
for( int i=n_hlayers_used-1 ; i>=0; i-- )
{
if( sample[i] == 1 )
{
Vec expectDecode(layers[i+1]->size);
expectDecode << layers[i+1]->expectation;
for( int j=0; j<expectDecode.size(); j++ )
expectDecode[j] = random_gen->binomial_sample(expectDecode[j]);
layers[i+1]->setExpectation(expectDecode);
}
connections[i]->setAsUpInput( layers[i+1]->expectation );
layers[i]->getAllActivations( connections[i], 0, false );
layers[i]->computeExpectation();
}
fantaImagesObtained[k+1] << layers[0]->expectation;
if( alwaysFromSrcImg )
layers[0]->setExpectation(srcImg);
}
return fantaImagesObtained;
}

| TVec< Vec > PLearn::DeepBeliefNet::fantasizeKTimeOnMultiSrcImg | ( | const int | KTime, |
| const Mat & | srcImg, | ||
| const Vec & | sample, | ||
| bool | alwaysFromSrcImg | ||
| ) | [private] |
Definition at line 3575 of file DeepBeliefNet.cc.
References PLearn::concat(), fantasizeKTime(), i, PLearn::TMat< T >::length(), and n.
Referenced by declareMethods().
{
int n=srcImg.length();
TVec<Vec> output(0);
for( int i=0; i<n; i++ )
{
const Vec img_i = srcImg(i);
TVec<Vec> outputTmp;
outputTmp = fantasizeKTime(KTime, img_i, sample, alwaysFromSrcImg);
output = concat(output, outputTmp);
}
return output;
}

| void PLearn::DeepBeliefNet::fineTuningStep | ( | const Vec & | input, |
| const Vec & | target, | ||
| Vec & | train_costs | ||
| ) |
Definition at line 2355 of file DeepBeliefNet.cc.
References activation_gradients, PLearn::argmax(), c, class_cost_index, PLearn::class_error(), class_gradient, class_output, classification_cost, classification_module, PLearn::TVec< T >::clear(), connections, PLearn::dot(), expectation_gradients, final_cost, final_cost_gradient, final_cost_index, final_cost_input, final_cost_value, final_module, greedy_target_activation_gradients, greedy_target_activations, greedy_target_connections, greedy_target_expectation_gradients, greedy_target_expectations, greedy_target_layers, greedy_target_probability_gradients, i, layers, PLearn::TVec< T >::length(), PLearn::multiplyScaledAdd(), n_classes, n_layers, nll_cost_index, PLearn::TVec< T >::resize(), PLearn::TVec< T >::subVec(), PLearn::TVec< T >::toMat(), and use_classification_cost.
Referenced by train().
{
final_cost_value.resize(0);
// fprop
layers[0]->expectation << input;
for( int i=0 ; i<n_layers-2 ; i++ )
{
if( greedy_target_layers.length() && greedy_target_layers[i] )
{
connections[i]->setAsDownInput( layers[i]->expectation );
layers[i+1]->getAllActivations( connections[i] );
greedy_target_layers[i]->activation.clear();
greedy_target_layers[i]->activation += greedy_target_layers[i]->bias;
for( int c=0; c<n_classes; c++ )
{
// Compute class free-energy
layers[i+1]->activation.toMat(layers[i+1]->size,1) += greedy_target_connections[i]->weights.column(c);
greedy_target_layers[i]->activation[c] -= layers[i+1]->freeEnergyContribution(layers[i+1]->activation);
// Compute class dependent expectation and store it
layers[i+1]->expectation_is_not_up_to_date();
layers[i+1]->computeExpectation();
greedy_target_expectations[i][c] << layers[i+1]->expectation;
// Remove class-dependent energy for next free-energy computations
layers[i+1]->activation.toMat(layers[i+1]->size,1) -= greedy_target_connections[i]->weights.column(c);
}
greedy_target_layers[i]->expectation_is_not_up_to_date();
greedy_target_layers[i]->computeExpectation();
// Computing next layer representation
layers[i+1]->expectation.clear();
Vec expectation = layers[i+1]->expectation;
for( int c=0; c<n_classes; c++ )
{
Vec expectation_c = greedy_target_expectations[i][c];
real p_c = greedy_target_layers[i]->expectation[c];
multiplyScaledAdd(expectation_c, real(1.), p_c, expectation);
}
}
else
{
connections[i]->setAsDownInput( layers[i]->expectation );
layers[i+1]->getAllActivations( connections[i] );
layers[i+1]->computeExpectation();
}
}
if( final_cost )
{
if( greedy_target_layers.length() && greedy_target_layers[n_layers-2] )
{
connections[n_layers-2]->setAsDownInput( layers[n_layers-2]->expectation );
layers[n_layers-1]->getAllActivations( connections[n_layers-2] );
greedy_target_layers[n_layers-2]->activation.clear();
greedy_target_layers[n_layers-2]->activation +=
greedy_target_layers[n_layers-2]->bias;
for( int c=0; c<n_classes; c++ )
{
// Compute class free-energy
layers[n_layers-1]->activation.toMat(layers[n_layers-1]->size,1) +=
greedy_target_connections[n_layers-2]->weights.column(c);
greedy_target_layers[n_layers-2]->activation[c] -=
layers[n_layers-1]->freeEnergyContribution(layers[n_layers-1]->activation);
// Compute class dependent expectation and store it
layers[n_layers-1]->expectation_is_not_up_to_date();
layers[n_layers-1]->computeExpectation();
greedy_target_expectations[n_layers-2][c] << layers[n_layers-1]->expectation;
// Remove class-dependent energy for next free-energy computations
layers[n_layers-1]->activation.toMat(layers[n_layers-1]->size,1) -=
greedy_target_connections[n_layers-2]->weights.column(c);
}
greedy_target_layers[n_layers-2]->expectation_is_not_up_to_date();
greedy_target_layers[n_layers-2]->computeExpectation();
// Computing next layer representation
layers[n_layers-1]->expectation.clear();
Vec expectation = layers[n_layers-1]->expectation;
for( int c=0; c<n_classes; c++ )
{
Vec expectation_c = greedy_target_expectations[n_layers-2][c];
real p_c = greedy_target_layers[n_layers-2]->expectation[c];
multiplyScaledAdd(expectation_c, real(1.), p_c, expectation);
}
}
else
{
connections[ n_layers-2 ]->setAsDownInput(
layers[ n_layers-2 ]->expectation );
layers[ n_layers-1 ]->getAllActivations( connections[ n_layers-2 ] );
layers[ n_layers-1 ]->computeExpectation();
}
if( final_module )
{
final_module->fprop( layers[ n_layers-1 ]->expectation,
final_cost_input );
final_cost->fprop( final_cost_input, target, final_cost_value );
final_cost->bpropUpdate( final_cost_input, target,
final_cost_value[0],
final_cost_gradient );
final_module->bpropUpdate( layers[ n_layers-1 ]->expectation,
final_cost_input,
expectation_gradients[ n_layers-1 ],
final_cost_gradient );
}
else
{
final_cost->fprop( layers[ n_layers-1 ]->expectation, target,
final_cost_value );
final_cost->bpropUpdate( layers[ n_layers-1 ]->expectation,
target, final_cost_value[0],
expectation_gradients[ n_layers-1 ] );
}
train_costs.subVec(final_cost_index, final_cost_value.length())
<< final_cost_value;
if( greedy_target_layers.length() && greedy_target_layers[n_layers-2] )
{
activation_gradients[n_layers-1].clear();
for( int c=0; c<n_classes; c++ )
{
greedy_target_expectation_gradients[n_layers-2][c] <<
expectation_gradients[ n_layers-1 ];
greedy_target_expectation_gradients[n_layers-2][c] *=
greedy_target_layers[n_layers-2]->expectation[c];
layers[ n_layers-1 ]->bpropUpdate(
greedy_target_activations[n_layers-2][c],
greedy_target_expectations[n_layers-2][c],
greedy_target_activation_gradients[n_layers-2][c],
greedy_target_expectation_gradients[n_layers-2][c] );
activation_gradients[n_layers-1] +=
greedy_target_activation_gradients[n_layers-2][c];
// Update target connections, with gradient from p(h_l | h_l-1, y)
multiplyScaledAdd( greedy_target_activation_gradients[n_layers-2][c].toMat(layers[n_layers-1]->size,1),
real(1.), -greedy_target_connections[n_layers-2]->learning_rate,
greedy_target_connections[n_layers-2]->weights.column(c));
greedy_target_probability_gradients[n_layers-2][c] =
dot( expectation_gradients[ n_layers-1 ],
greedy_target_expectations[ n_layers-2 ][c] );
}
// Update bias
greedy_target_layers[n_layers-2]->bpropUpdate(
greedy_target_layers[n_layers-2]->expectation, // Isn't used
greedy_target_layers[n_layers-2]->expectation,
greedy_target_probability_gradients[n_layers-2],
greedy_target_probability_gradients[n_layers-2] );
for( int c=0; c<n_classes; c++ )
{
layers[n_layers-1]->freeEnergyContributionGradient(
greedy_target_activations[n_layers-2][c],
greedy_target_activation_gradients[n_layers-2][c], // Overwrite previous activation gradient
-greedy_target_probability_gradients[n_layers-2][c] );
activation_gradients[n_layers-1] +=
greedy_target_activation_gradients[n_layers-2][c];
// Update target connections, with gradient from p(y | h_l-1 )
multiplyScaledAdd( greedy_target_activation_gradients[n_layers-2][c].toMat(layers[n_layers-1]->size,1),
real(1.), -greedy_target_connections[n_layers-2]->learning_rate,
greedy_target_connections[n_layers-2]->weights.column(c));
}
connections[ n_layers-2 ]->bpropUpdate(
layers[ n_layers-2 ]->expectation,
layers[ n_layers-1 ]->activation, //Not really, but this isn't used for matrix connections
expectation_gradients[ n_layers-2 ],
activation_gradients[ n_layers-1 ] );
}
else
{
layers[ n_layers-1 ]->bpropUpdate( layers[ n_layers-1 ]->activation,
layers[ n_layers-1 ]->expectation,
activation_gradients[ n_layers-1 ],
expectation_gradients[ n_layers-1 ]
);
connections[ n_layers-2 ]->bpropUpdate(
layers[ n_layers-2 ]->expectation,
layers[ n_layers-1 ]->activation,
expectation_gradients[ n_layers-2 ],
activation_gradients[ n_layers-1 ] );
}
}
else {
expectation_gradients[ n_layers-2 ].clear();
}
if( use_classification_cost )
{
classification_module->fprop( layers[ n_layers-2 ]->expectation,
class_output );
real nll_cost;
// This doesn't work. gcc bug?
// classification_cost->fprop( class_output, target, cost );
classification_cost->CostModule::fprop( class_output, target,
nll_cost );
real class_error =
( argmax(class_output) == (int) round(target[0]) ) ? 0
: 1;
train_costs[nll_cost_index] = nll_cost;
train_costs[class_cost_index] = class_error;
classification_cost->bpropUpdate( class_output, target, nll_cost,
class_gradient );
classification_module->bpropUpdate( layers[ n_layers-2 ]->expectation,
class_output,
expectation_gradients[n_layers-2],
class_gradient,
true );
}
for( int i=n_layers-2 ; i>0 ; i-- )
{
if( greedy_target_layers.length() && greedy_target_layers[i] )
{
activation_gradients[i-1].clear();
for( int c=0; c<n_classes; c++ )
{
greedy_target_expectation_gradients[i-1][c] <<
expectation_gradients[ i ];
greedy_target_expectation_gradients[i-1][c] *=
greedy_target_layers[i-1]->expectation[c];
layers[ i ]->bpropUpdate(
greedy_target_activations[i-1][c],
greedy_target_expectations[i-1][c],
greedy_target_activation_gradients[i-1][c],
greedy_target_expectation_gradients[i-1][c] );
activation_gradients[i ] +=
greedy_target_activation_gradients[i-1][c];
// Update target connections, with gradient from p(h_l | h_l-1, y)
multiplyScaledAdd( greedy_target_activation_gradients[i-1][c].toMat(layers[i]->size,1),
real(1.), -greedy_target_connections[i-1]->learning_rate,
greedy_target_connections[i-1]->weights.column(c));
greedy_target_probability_gradients[i-1][c] =
dot( expectation_gradients[ i ],
greedy_target_expectations[ i-1 ][c] );
}
// Update bias
greedy_target_layers[i-1]->bpropUpdate(
greedy_target_layers[i-1]->expectation, // Isn't used
greedy_target_layers[i-1]->expectation,
greedy_target_probability_gradients[i-1],
greedy_target_probability_gradients[i-1] );
for( int c=0; c<n_classes; c++ )
{
layers[i]->freeEnergyContributionGradient(
greedy_target_activations[i-1][c],
greedy_target_activation_gradients[i-1][c], // Overwrite previous activation gradient
-greedy_target_probability_gradients[i-1][c] );
activation_gradients[i] +=
greedy_target_activation_gradients[i-1][c];
// Update target connections, with gradient from p(y | h_l-1 )
multiplyScaledAdd( greedy_target_activation_gradients[i-1][c].toMat(layers[i]->size,1),
real(1.), -greedy_target_connections[i-1]->learning_rate,
greedy_target_connections[i-1]->weights.column(c));
}
connections[ i-1 ]->bpropUpdate(
layers[ i-1 ]->expectation,
layers[ i ]->activation, //Not really, but this isn't used for matrix connections
expectation_gradients[ i-1 ],
activation_gradients[ i ] );
}
else
{
layers[i]->bpropUpdate( layers[i]->activation,
layers[i]->expectation,
activation_gradients[i],
expectation_gradients[i] );
connections[i-1]->bpropUpdate( layers[i-1]->expectation,
layers[i]->activation,
expectation_gradients[i-1],
activation_gradients[i] );
}
}
}

| void PLearn::DeepBeliefNet::fineTuningStep | ( | const Mat & | inputs, |
| const Mat & | targets, | ||
| Mat & | train_costs | ||
| ) |
Definition at line 2659 of file DeepBeliefNet.cc.
References activations_gradients, PLearn::TMat< T >::clear(), PLearn::TVec< T >::clear(), PLearn::TMat< T >::column(), connections, expectations_gradients, final_cost, final_cost_gradients, final_cost_index, final_cost_inputs, final_cost_values, final_module, greedy_target_layers, i, layer_inputs, layers, PLearn::TVec< T >::length(), minibatch_size, n_layers, optimized_costs, PLERROR, reconstruct_layerwise, reconstruction_cost_index, PLearn::TMat< T >::resize(), PLearn::TMat< T >::subMatColumns(), use_classification_cost, and PLearn::TMat< T >::width().
{
if( greedy_target_layers.length() )
PLERROR("In DeepBeliefNet::fineTuningStep(): greedy_target_layers not implemented\n"
"for minibatch setting");
final_cost_values.resize(0, 0);
// fprop
layers[0]->getExpectations() << inputs;
for( int i=0 ; i<n_layers-2 ; i++ )
{
connections[i]->setAsDownInputs( layers[i]->getExpectations() );
layers[i+1]->getAllActivations( connections[i], 0, true );
layers[i+1]->computeExpectations();
}
if( final_cost )
{
connections[ n_layers-2 ]->setAsDownInputs(
layers[ n_layers-2 ]->getExpectations() );
// TODO Also ensure getAllActivations fills everything.
layers[ n_layers-1 ]->getAllActivations(connections[n_layers-2],
0, true);
layers[ n_layers-1 ]->computeExpectations();
if( final_module )
{
final_cost_inputs.resize(minibatch_size,
final_module->output_size);
final_module->fprop( layers[ n_layers-1 ]->getExpectations(),
final_cost_inputs );
final_cost->fprop( final_cost_inputs, targets, final_cost_values );
// TODO This extra memory copy is annoying: how can we avoid it?
optimized_costs << final_cost_values.column(0);
final_cost->bpropUpdate( final_cost_inputs, targets,
optimized_costs,
final_cost_gradients );
final_module->bpropUpdate( layers[ n_layers-1 ]->getExpectations(),
final_cost_inputs,
expectations_gradients[ n_layers-1 ],
final_cost_gradients );
}
else
{
final_cost->fprop( layers[ n_layers-1 ]->getExpectations(), targets,
final_cost_values );
optimized_costs << final_cost_values.column(0);
final_cost->bpropUpdate( layers[ n_layers-1 ]->getExpectations(),
targets, optimized_costs,
expectations_gradients[ n_layers-1 ] );
}
train_costs.subMatColumns(final_cost_index, final_cost_values.width())
<< final_cost_values;
layers[ n_layers-1 ]->bpropUpdate( layers[ n_layers-1 ]->activations,
layers[ n_layers-1 ]->getExpectations(),
activations_gradients[ n_layers-1 ],
expectations_gradients[ n_layers-1 ]
);
connections[ n_layers-2 ]->bpropUpdate(
layers[ n_layers-2 ]->getExpectations(),
layers[ n_layers-1 ]->activations,
expectations_gradients[ n_layers-2 ],
activations_gradients[ n_layers-1 ] );
}
else {
expectations_gradients[ n_layers-2 ].clear();
}
if( use_classification_cost )
{
PLERROR("DeepBeliefNet::fineTuningStep - Not implemented for "
"mini-batches");
/*
classification_module->fprop( layers[ n_layers-2 ]->expectation,
class_output );
real nll_cost;
// This doesn't work. gcc bug?
// classification_cost->fprop( class_output, target, cost );
classification_cost->CostModule::fprop( class_output, target,
nll_cost );
real class_error =
( argmax(class_output) == (int) round(target[0]) ) ? 0
: 1;
train_costs[nll_cost_index] = nll_cost;
train_costs[class_cost_index] = class_error;
classification_cost->bpropUpdate( class_output, target, nll_cost,
class_gradient );
classification_module->bpropUpdate( layers[ n_layers-2 ]->expectation,
class_output,
expectation_gradients[n_layers-2],
class_gradient,
true );
*/
}
for( int i=n_layers-2 ; i>0 ; i-- )
{
layers[i]->bpropUpdate( layers[i]->activations,
layers[i]->getExpectations(),
activations_gradients[i],
expectations_gradients[i] );
connections[i-1]->bpropUpdate( layers[i-1]->getExpectations(),
layers[i]->activations,
expectations_gradients[i-1],
activations_gradients[i] );
}
// do it AFTER the bprop to avoid interfering with activations used in bprop
// (and do not worry that the weights have changed a bit). This is incoherent
// with the current implementation in the greedy stage.
if ( reconstruct_layerwise )
{
Mat rc = train_costs.column(reconstruction_cost_index);
rc.clear();
for( int index=0 ; index<n_layers-1 ; index++ )
{
layer_inputs.resize(minibatch_size,layers[index]->size);
layer_inputs << layers[index]->getExpectations();
connections[index]->setAsUpInputs(layers[index+1]->getExpectations());
layers[index]->getAllActivations(connections[index], 0, true);
layers[index]->fpropNLL(layer_inputs, train_costs.column(reconstruction_cost_index+index+1));
rc += train_costs.column(reconstruction_cost_index+index+1);
}
}
}
| void PLearn::DeepBeliefNet::forget | ( | ) | [virtual] |
(Re-)initializes the PLearner in its fresh state (that state may depend on the 'seed' option) and sets 'stage' back to 0 (this is the stage of a fresh learner!).
Reimplemented from PLearn::PLearner.
Definition at line 1040 of file DeepBeliefNet.cc.
References classification_cost, classification_module, connections, cumulative_testing_time, cumulative_training_time, final_cost, final_module, PLearn::PLearner::forget(), generative_connections, greedy_target_connections, greedy_target_layers, i, PLearn::TVec< T >::isEmpty(), layers, PLearn::TVec< T >::length(), n_layers, partial_costs, up_down_stage, and use_classification_cost.
{
inherited::forget();
for( int i=0 ; i<n_layers ; i++ )
layers[i]->forget();
for( int i=0 ; i<n_layers-1 ; i++ )
connections[i]->forget();
if( use_classification_cost )
{
classification_cost->forget();
classification_module->forget();
}
if( final_module )
final_module->forget();
if( final_cost )
final_cost->forget();
if( !partial_costs.isEmpty() )
for( int i=0 ; i<n_layers-1 ; i++ )
if( partial_costs[i] )
partial_costs[i]->forget();
for( int i=0 ; i<generative_connections.length() ; i++ )
generative_connections[i]->forget();
for( int i=0; i<greedy_target_connections.length(); i++ )
greedy_target_connections[i]->forget();
for( int i=0; i<greedy_target_layers.length(); i++ )
greedy_target_layers[i]->forget();
cumulative_training_time = 0;
cumulative_testing_time = 0;
up_down_stage = 0;
}
| OptionList & PLearn::DeepBeliefNet::getOptionList | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 55 of file DeepBeliefNet.cc.
| OptionMap & PLearn::DeepBeliefNet::getOptionMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 55 of file DeepBeliefNet.cc.
| RemoteMethodMap & PLearn::DeepBeliefNet::getRemoteMethodMap | ( | ) | const [virtual] |
Reimplemented from PLearn::Object.
Definition at line 55 of file DeepBeliefNet.cc.
| TVec< string > PLearn::DeepBeliefNet::getTestCostNames | ( | ) | const [virtual] |
Returns the names of the costs computed by computeCostsFromOutpus (and thus the test method).
Implements PLearn::PLearner.
Definition at line 3521 of file DeepBeliefNet.cc.
References cost_names.
Referenced by test().
{
// Return the names of the costs computed by computeCostsFromOutputs
// (these may or may not be exactly the same as what's returned by
// getTrainCostNames).
return cost_names;
}

| TVec< string > PLearn::DeepBeliefNet::getTrainCostNames | ( | ) | const [virtual] |
Returns the names of the objective costs that the train method computes and for which it updates the VecStatsCollector train_stats.
Implements PLearn::PLearner.
Definition at line 3530 of file DeepBeliefNet.cc.
References cost_names.
Referenced by train().
{
return cost_names;
}

Definition at line 1966 of file DeepBeliefNet.cc.
References activation_gradients, c, cd_decrease_ct, cd_learning_rate, PLearn::TVec< T >::clear(), connections, contrastiveDivergenceStep(), corrupt_input(), corrupted_pos_down_val, cumulative_schedule, expectation_gradients, PLearn::fast_exact_is_equal(), PLearn::fill_one_hot(), grad_decrease_ct, grad_learning_rate, greedy_joint_connections, greedy_joint_layers, greedy_target_connections, greedy_target_expectations, greedy_target_layers, i, PLearn::TVec< T >::isEmpty(), layers, PLearn::TVec< T >::length(), PLearn::multiplyScaledAdd(), n_classes, n_layers, partial_costs, PLASSERT, PLearn::TVec< T >::resize(), PLearn::PLearner::stage, PLearn::TVec< T >::toMat(), and use_corrupted_posDownVal.
Referenced by train().
{
real lr;
PLASSERT( index < n_layers );
layers[0]->expectation << input;
for( int i=0 ; i<=index ; i++ )
{
if( greedy_target_layers.length() && greedy_target_layers[i] )
{
connections[i]->setAsDownInput( layers[i]->expectation );
layers[i+1]->getAllActivations( connections[i] );
if( i != index )
{
greedy_target_layers[i]->activation.clear();
greedy_target_layers[i]->activation += greedy_target_layers[i]->bias;
for( int c=0; c<n_classes; c++ )
{
// Compute class free-energy
layers[i+1]->activation.toMat(layers[i+1]->size,1) +=
greedy_target_connections[i]->weights.column(c);
greedy_target_layers[i]->activation[c] -=
layers[i+1]->freeEnergyContribution(layers[i+1]->activation);
// Compute class dependent expectation and store it
layers[i+1]->expectation_is_not_up_to_date();
layers[i+1]->computeExpectation();
greedy_target_expectations[i][c] << layers[i+1]->expectation;
// Remove class-dependent energy for next free-energy computations
layers[i+1]->activation.toMat(layers[i+1]->size,1) -= greedy_target_connections[i]->weights.column(c);
}
greedy_target_layers[i]->expectation_is_not_up_to_date();
greedy_target_layers[i]->computeExpectation();
// Computing next layer representation
layers[i+1]->expectation.clear();
Vec expectation = layers[i+1]->expectation;
for( int c=0; c<n_classes; c++ )
{
Vec expectation_c = greedy_target_expectations[i][c];
real p_c = greedy_target_layers[i]->expectation[c];
multiplyScaledAdd(expectation_c, real(1.), p_c, expectation);
}
}
else
{
fill_one_hot( greedy_target_layers[i]->expectation,
(int) round(target[0]), real(0.), real(1.) );
}
}
else
{
if( i == index && use_corrupted_posDownVal == "for_cd_fprop" )
{
corrupted_pos_down_val.resize( layers[i]->size );
corrupt_input( layers[i]->expectation, corrupted_pos_down_val, index );
connections[i]->setAsDownInput( corrupted_pos_down_val );
}
else
connections[i]->setAsDownInput( layers[i]->expectation );
layers[i+1]->getAllActivations( connections[i] );
layers[i+1]->computeExpectation();
}
}
if( !partial_costs.isEmpty() && partial_costs[ index ] )
{
// put appropriate learning rate
if( !fast_exact_is_equal( grad_decrease_ct, 0. ) )
lr = grad_learning_rate /
(1. + grad_decrease_ct *
(stage - cumulative_schedule[index]));
else
lr = grad_learning_rate;
partial_costs[ index ]->setLearningRate( lr );
connections[ index ]->setLearningRate( lr );
layers[ index+1 ]->setLearningRate( lr );
// Backward pass
real cost;
partial_costs[ index ]->fprop( layers[ index+1 ]->expectation,
target, cost );
partial_costs[ index ]->bpropUpdate( layers[ index+1 ]->expectation,
target, cost,
expectation_gradients[ index+1 ]
);
layers[ index+1 ]->bpropUpdate( layers[ index+1 ]->activation,
layers[ index+1 ]->expectation,
activation_gradients[ index+1 ],
expectation_gradients[ index+1 ] );
connections[ index ]->bpropUpdate( layers[ index ]->expectation,
layers[ index+1 ]->activation,
expectation_gradients[ index ],
activation_gradients[ index+1 ] );
// put back old learning rate
if( !fast_exact_is_equal( cd_decrease_ct, 0. ) )
lr = cd_learning_rate / (1. + cd_decrease_ct *
(stage - cumulative_schedule[index]));
else
lr = cd_learning_rate;
connections[ index ]->setLearningRate( lr );
layers[ index+1 ]->setLearningRate( lr );
}
if( greedy_target_layers.length() && greedy_target_layers[index] )
{
contrastiveDivergenceStep( greedy_joint_layers[ index ],
greedy_joint_connections[ index ],
layers[ index+1 ],
index, false);
}
else
{
contrastiveDivergenceStep( layers[ index ],
connections[ index ],
layers[ index+1 ],
index, true);
}
}

| void PLearn::DeepBeliefNet::greedyStep | ( | const Mat & | inputs, |
| const Mat & | targets, | ||
| int | index, | ||
| Mat & | train_costs_m | ||
| ) |
Definition at line 2097 of file DeepBeliefNet.cc.
References activations_gradients, cd_decrease_ct, cd_learning_rate, PLearn::TMat< T >::column(), connections, contrastiveDivergenceStep(), cumulative_schedule, expectations_gradients, PLearn::fast_exact_is_equal(), grad_decrease_ct, grad_learning_rate, greedy_target_layers, i, PLearn::TVec< T >::isEmpty(), layer_inputs, layers, PLearn::TVec< T >::length(), minibatch_size, n_layers, partial_costs, PLASSERT, PLERROR, reconstruct_layerwise, reconstruction_cost_index, PLearn::TMat< T >::resize(), and PLearn::PLearner::stage.
{
real lr;
PLASSERT( index < n_layers );
layers[0]->setExpectations(inputs);
if( greedy_target_layers.length() && greedy_target_layers[0] )
PLERROR("In DeepBeliefNet::greedyStep(): greedy_target_layers not implemented\n"
"for minibatch setting");
for( int i=0 ; i<=index ; i++ )
{
connections[i]->setAsDownInputs( layers[i]->getExpectations() );
layers[i+1]->getAllActivations( connections[i], 0, true );
layers[i+1]->computeExpectations();
}
if( !partial_costs.isEmpty() && partial_costs[ index ] )
{
// put appropriate learning rate
if( !fast_exact_is_equal( grad_decrease_ct, 0. ) )
lr = grad_learning_rate /
(1. + grad_decrease_ct *
(stage - cumulative_schedule[index]));
else
lr = grad_learning_rate;
partial_costs[ index ]->setLearningRate( lr );
connections[ index ]->setLearningRate( lr );
layers[ index+1 ]->setLearningRate( lr );
// Backward pass
Vec costs;
partial_costs[ index ]->fprop( layers[ index+1 ]->getExpectations(),
targets, costs );
partial_costs[ index ]->bpropUpdate(layers[index+1]->getExpectations(),
targets, costs,
expectations_gradients[ index+1 ]
);
layers[ index+1 ]->bpropUpdate( layers[ index+1 ]->activations,
layers[ index+1 ]->getExpectations(),
activations_gradients[ index+1 ],
expectations_gradients[ index+1 ] );
connections[ index ]->bpropUpdate( layers[ index ]->getExpectations(),
layers[ index+1 ]->activations,
expectations_gradients[ index ],
activations_gradients[ index+1 ] );
// put back old learning rate
if( !fast_exact_is_equal( cd_decrease_ct, 0. ) )
lr = cd_learning_rate / (1. + cd_decrease_ct *
(stage - cumulative_schedule[index]));
else
lr = cd_learning_rate;
connections[ index ]->setLearningRate( lr );
layers[ index+1 ]->setLearningRate( lr );
}
if (reconstruct_layerwise)
{
layer_inputs.resize(minibatch_size,layers[index]->size);
layer_inputs << layers[index]->getExpectations(); // we will perturb these, so save them
connections[index]->setAsUpInputs(layers[index+1]->getExpectations());
layers[index]->getAllActivations(connections[index], 0, true);
layers[index]->fpropNLL(layer_inputs, train_costs_m.column(reconstruction_cost_index+index+1));
Mat rc = train_costs_m.column(reconstruction_cost_index);
rc += train_costs_m.column(reconstruction_cost_index+index+1);
layers[index]->setExpectations(layer_inputs); // and restore them here
}
contrastiveDivergenceStep( layers[ index ],
connections[ index ],
layers[ index+1 ],
index, true);
}
Definition at line 2183 of file DeepBeliefNet.cc.
References activation_gradients, batch_size, cd_decrease_ct, cd_learning_rate, classification_module, connections, contrastiveDivergenceStep(), cumulative_schedule, expectation_gradients, PLearn::fast_exact_is_equal(), PLearn::fill_one_hot(), PLearn::get_pointer(), grad_decrease_ct, grad_learning_rate, i, PLearn::TVec< T >::isEmpty(), joint_layer, layers, n_layers, partial_costs, PLASSERT, PLASSERT_MSG, and PLearn::PLearner::stage.
Referenced by train().
{
real lr;
PLASSERT( joint_layer );
PLASSERT_MSG(batch_size == 1, "Not implemented for mini-batches");
layers[0]->expectation << input;
for( int i=0 ; i<n_layers-2 ; i++ )
{
connections[i]->setAsDownInput( layers[i]->expectation );
layers[i+1]->getAllActivations( connections[i] );
layers[i+1]->computeExpectation();
}
if( !partial_costs.isEmpty() && partial_costs[ n_layers-2 ] )
{
// Deterministic forward pass
connections[ n_layers-2 ]->setAsDownInput(
layers[ n_layers-2 ]->expectation );
layers[ n_layers-1 ]->getAllActivations( connections[ n_layers-2 ] );
layers[ n_layers-1 ]->computeExpectation();
// put appropriate learning rate
if( !fast_exact_is_equal( grad_decrease_ct, 0. ) )
lr = grad_learning_rate
/ (1. + grad_decrease_ct *
(stage - cumulative_schedule[n_layers-2]));
else
lr = grad_learning_rate;
partial_costs[ n_layers-2 ]->setLearningRate( lr );
connections[ n_layers-2 ]->setLearningRate( lr );
layers[ n_layers-1 ]->setLearningRate( lr );
// Backward pass
real cost;
partial_costs[ n_layers-2 ]->fprop( layers[ n_layers-1 ]->expectation,
target, cost );
partial_costs[ n_layers-2 ]->bpropUpdate(
layers[ n_layers-1 ]->expectation, target, cost,
expectation_gradients[ n_layers-1 ] );
layers[ n_layers-1 ]->bpropUpdate( layers[ n_layers-1 ]->activation,
layers[ n_layers-1 ]->expectation,
activation_gradients[ n_layers-1 ],
expectation_gradients[ n_layers-1 ]
);
connections[ n_layers-2 ]->bpropUpdate(
layers[ n_layers-2 ]->expectation,
layers[ n_layers-1 ]->activation,
expectation_gradients[ n_layers-2 ],
activation_gradients[ n_layers-1 ] );
// put back old learning rate
if( !fast_exact_is_equal( cd_decrease_ct, 0. ) )
lr = cd_learning_rate
/ (1. + cd_decrease_ct *
(stage - cumulative_schedule[n_layers-2]));
else
lr = cd_learning_rate;
connections[ n_layers-2 ]->setLearningRate( lr );
layers[ n_layers-1 ]->setLearningRate( lr );
}
Vec target_exp = classification_module->target_layer->expectation;
fill_one_hot( target_exp, (int) round(target[0]), real(0.), real(1.) );
contrastiveDivergenceStep(
get_pointer( joint_layer ),
get_pointer( classification_module->joint_connection ),
layers[ n_layers-1 ], n_layers-2);
}

Definition at line 2260 of file DeepBeliefNet.cc.
References PLCHECK_MSG.
{
PLCHECK_MSG(false, "Not implemented for mini-batches");
}
| void PLearn::DeepBeliefNet::makeDeepCopyFromShallowCopy | ( | CopiesMap & | copies | ) | [virtual] |
Transforms a shallow copy into a deep copy.
Reimplemented from PLearn::PLearner.
Definition at line 952 of file DeepBeliefNet.cc.
References activation_gradients, activations_gradients, cd_neg_down_vals, cd_neg_up_vals, class_gradient, class_output, classification_cost, classification_module, connections, corrupted_pos_down_val, cost_names, cumulative_schedule, PLearn::deepCopyField(), down_sample, expectation_gradients, expectation_indices, expectations_gradients, final_cost, final_cost_gradient, final_cost_gradients, final_cost_input, final_cost_inputs, final_cost_output, final_cost_value, final_cost_values, final_module, generative_connections, gibbs_down_state, greedy_joint_connections, greedy_joint_layers, greedy_target_activation_gradients, greedy_target_activations, greedy_target_connections, greedy_target_expectation_gradients, greedy_target_expectations, greedy_target_layers, greedy_target_probability_gradients, joint_layer, layer_input, layer_inputs, layers, PLearn::PLearner::makeDeepCopyFromShallowCopy(), mf_cd_neg_down_val, mf_cd_neg_down_vals, mf_cd_neg_up_val, mf_cd_neg_up_vals, optimized_costs, partial_costs, partial_costs_indices, pos_down_val, pos_down_vals, pos_up_val, pos_up_vals, reconstruction_costs, save_layer_activation, save_layer_activations, save_layer_expectation, save_layer_expectations, target_one_hot, timer, training_schedule, and up_sample.
{
inherited::makeDeepCopyFromShallowCopy(copies);
deepCopyField(training_schedule, copies);
deepCopyField(layers, copies);
deepCopyField(connections, copies);
deepCopyField(greedy_target_layers, copies);
deepCopyField(greedy_target_connections,copies);
deepCopyField(final_module, copies);
deepCopyField(final_cost, copies);
deepCopyField(partial_costs, copies);
deepCopyField(classification_module, copies);
deepCopyField(cost_names, copies);
deepCopyField(timer, copies);
deepCopyField(classification_cost, copies);
deepCopyField(joint_layer, copies);
deepCopyField(activation_gradients, copies);
deepCopyField(activations_gradients, copies);
deepCopyField(expectation_gradients, copies);
deepCopyField(expectations_gradients, copies);
deepCopyField(greedy_target_expectations,copies);
deepCopyField(greedy_target_activations, copies);
deepCopyField(greedy_target_expectation_gradients,copies);
deepCopyField(greedy_target_activation_gradients,copies);
deepCopyField(greedy_target_probability_gradients,copies);
deepCopyField(greedy_joint_layers , copies);
deepCopyField(greedy_joint_connections, copies);
deepCopyField(final_cost_input, copies);
deepCopyField(final_cost_inputs, copies);
deepCopyField(final_cost_value, copies);
deepCopyField(final_cost_values, copies);
deepCopyField(final_cost_output, copies);
deepCopyField(class_output, copies);
deepCopyField(class_gradient, copies);
deepCopyField(final_cost_gradient, copies);
deepCopyField(final_cost_gradients, copies);
deepCopyField(save_layer_activation, copies);
deepCopyField(save_layer_expectation, copies);
deepCopyField(save_layer_activations, copies);
deepCopyField(save_layer_expectations, copies);
deepCopyField(pos_down_val, copies);
deepCopyField(corrupted_pos_down_val, copies);
deepCopyField(pos_up_val, copies);
deepCopyField(pos_down_vals, copies);
deepCopyField(pos_up_vals, copies);
deepCopyField(cd_neg_down_vals, copies);
deepCopyField(cd_neg_up_vals, copies);
deepCopyField(mf_cd_neg_down_vals, copies);
deepCopyField(mf_cd_neg_up_vals, copies);
deepCopyField(mf_cd_neg_down_val, copies);
deepCopyField(mf_cd_neg_up_val, copies);
deepCopyField(gibbs_down_state, copies);
deepCopyField(optimized_costs, copies);
deepCopyField(target_one_hot, copies);
deepCopyField(reconstruction_costs, copies);
deepCopyField(partial_costs_indices, copies);
deepCopyField(cumulative_schedule, copies);
deepCopyField(layer_input, copies);
deepCopyField(layer_inputs, copies);
deepCopyField(generative_connections, copies);
deepCopyField(up_sample, copies);
deepCopyField(down_sample, copies);
deepCopyField(expectation_indices, copies);
}

Definition at line 1480 of file DeepBeliefNet.cc.
References activation_gradients, PLearn::argmax(), batch_size, cd_decrease_ct, cd_learning_rate, class_cost_index, PLearn::class_error(), class_gradient, class_output, classification_cost, classification_module, PLearn::TVec< T >::clear(), connections, contrastiveDivergenceStep(), expectation_gradients, PLearn::fast_exact_is_equal(), PLearn::fill_one_hot(), final_cost, final_cost_gradient, final_cost_index, final_cost_input, final_cost_value, final_module, PLearn::get_pointer(), grad_decrease_ct, grad_learning_rate, greedy_target_layers, i, PLearn::TVec< T >::isEmpty(), joint_layer, layers, PLearn::TVec< T >::length(), n_layers, nll_cost_index, partial_costs, partial_costs_indices, PLASSERT, PLERROR, PLearn::TVec< T >::resize(), save_layer_activation, save_layer_expectation, PLearn::PLearner::stage, PLearn::TVec< T >::subVec(), top_layer_joint_cd, and use_classification_cost.
Referenced by train().
{
real lr;
PLASSERT(batch_size == 1);
if( greedy_target_layers.length() )
PLERROR("In DeepBeliefNet::onlineStep(): greedy_target_layers not implemented\n"
"for online setting");
TVec<Vec> cost;
if (!partial_costs.isEmpty())
cost.resize(n_layers-1);
layers[0]->expectation << input;
// FORWARD PHASE
//Vec layer_input;
for( int i=0 ; i<n_layers-1 ; i++ )
{
// mean-field fprop from layer i to layer i+1
connections[i]->setAsDownInput( layers[i]->expectation );
// this does the actual matrix-vector computation
layers[i+1]->getAllActivations( connections[i] );
layers[i+1]->computeExpectation();
// propagate into local cost associated to output of layer i+1
if( !partial_costs.isEmpty() && partial_costs[ i ] )
{
partial_costs[ i ]->fprop( layers[ i+1 ]->expectation,
target, cost[i] );
// Backward pass
// first time we set these gradients: do not accumulate
partial_costs[ i ]->bpropUpdate( layers[ i+1 ]->expectation,
target, cost[i][0],
expectation_gradients[ i+1 ] );
train_costs.subVec(partial_costs_indices[i], cost[i].length())
<< cost[i];
}
else
expectation_gradients[i+1].clear();
}
// top layer may be connected to a final_module followed by a
// final_cost and / or may be used to predict class probabilities
// through a joint classification_module
if ( final_cost )
{
if( final_module )
{
final_module->fprop( layers[ n_layers-1 ]->expectation,
final_cost_input );
final_cost->fprop( final_cost_input, target,
final_cost_value );
final_cost->bpropUpdate( final_cost_input, target,
final_cost_value[0],
final_cost_gradient );
final_module->bpropUpdate(
layers[ n_layers-1 ]->expectation,
final_cost_input,
expectation_gradients[ n_layers-1 ],
final_cost_gradient, true );
}
else
{
final_cost->fprop( layers[ n_layers-1 ]->expectation,
target,
final_cost_value );
final_cost->bpropUpdate( layers[ n_layers-1 ]->expectation,
target, final_cost_value[0],
expectation_gradients[n_layers-1],
true);
}
train_costs.subVec(final_cost_index, final_cost_value.length())
<< final_cost_value;
}
if (final_cost || (!partial_costs.isEmpty() && partial_costs[n_layers-2]))
{
if( !fast_exact_is_equal( grad_decrease_ct, 0. ) )
lr = grad_learning_rate / (1. + grad_decrease_ct * stage );
else
lr = grad_learning_rate;
layers[n_layers-1]->setLearningRate( lr );
connections[n_layers-2]->setLearningRate( lr );
layers[ n_layers-1 ]->bpropUpdate( layers[ n_layers-1 ]->activation,
layers[ n_layers-1 ]->expectation,
activation_gradients[ n_layers-1 ],
expectation_gradients[ n_layers-1 ],
false);
connections[ n_layers-2 ]->bpropUpdate(
layers[ n_layers-2 ]->expectation,
layers[ n_layers-1 ]->activation,
expectation_gradients[ n_layers-2 ],
activation_gradients[ n_layers-1 ],
true);
// accumulate into expectation_gradients[n_layers-2]
// because a partial cost may have already put a gradient there
}
if( use_classification_cost )
{
classification_module->fprop( layers[ n_layers-2 ]->expectation,
class_output );
real nll_cost;
// This doesn't work. gcc bug?
// classification_cost->fprop( class_output, target, cost );
classification_cost->CostModule::fprop( class_output, target,
nll_cost );
real class_error =
( argmax(class_output) == (int) round(target[0]) ) ? 0: 1;
train_costs[nll_cost_index] = nll_cost;
train_costs[class_cost_index] = class_error;
classification_cost->bpropUpdate( class_output, target, nll_cost,
class_gradient );
classification_module->bpropUpdate( layers[ n_layers-2 ]->expectation,
class_output,
expectation_gradients[n_layers-2],
class_gradient,
true );
if( top_layer_joint_cd )
{
// set the input of the joint layer
Vec target_exp = classification_module->target_layer->expectation;
fill_one_hot( target_exp, (int) round(target[0]), real(0.), real(1.) );
if( !fast_exact_is_equal( cd_decrease_ct, 0. ) )
lr = cd_learning_rate / (1. + cd_decrease_ct * stage );
else
lr = cd_learning_rate;
joint_layer->setLearningRate( lr );
layers[ n_layers-1 ]->setLearningRate( lr );
classification_module->joint_connection->setLearningRate( lr );
save_layer_activation.resize(layers[ n_layers-2 ]->size);
save_layer_activation << layers[ n_layers-2 ]->activation;
save_layer_expectation.resize(layers[ n_layers-2 ]->size);
save_layer_expectation << layers[ n_layers-2 ]->expectation;
contrastiveDivergenceStep(
get_pointer(joint_layer),
get_pointer(classification_module->joint_connection),
layers[ n_layers-1 ], n_layers-2);
layers[ n_layers-2 ]->activation << save_layer_activation;
layers[ n_layers-2 ]->expectation << save_layer_expectation;
}
}
// DOWNWARD PHASE (the downward phase for top layer is already done above,
// except for the contrastive divergence step in the case where either
// 'use_classification_cost' or 'top_layer_joint_cd' is false).
for( int i=n_layers-2 ; i>=0 ; i-- )
{
if (i <= n_layers - 3) {
if( !fast_exact_is_equal( grad_decrease_ct, 0. ) )
lr = grad_learning_rate / (1. + grad_decrease_ct * stage );
else
lr = grad_learning_rate;
connections[ i ]->setLearningRate( lr );
layers[ i+1 ]->setLearningRate( lr );
layers[i+1]->bpropUpdate( layers[i+1]->activation,
layers[i+1]->expectation,
activation_gradients[i+1],
expectation_gradients[i+1] );
connections[i]->bpropUpdate( layers[i]->expectation,
layers[i+1]->activation,
expectation_gradients[i],
activation_gradients[i+1],
true);
}
if (i <= n_layers - 3 || !use_classification_cost ||
!top_layer_joint_cd) {
// N.B. the contrastiveDivergenceStep changes the activation and
// expectation fields of top layer of the RBM, so it must be
// done last
if( !fast_exact_is_equal( cd_decrease_ct, 0. ) )
lr = cd_learning_rate / (1. + cd_decrease_ct * stage );
else
lr = cd_learning_rate;
layers[i]->setLearningRate( lr );
layers[i+1]->setLearningRate( lr );
connections[i]->setLearningRate( lr );
if( i > 0 )
{
save_layer_activation.resize(layers[i]->size);
save_layer_activation << layers[i]->activation;
save_layer_expectation.resize(layers[i]->size);
save_layer_expectation << layers[i]->expectation;
}
contrastiveDivergenceStep( layers[ i ],
connections[ i ],
layers[ i+1 ] ,
i, true);
if( i > 0 )
{
layers[i]->activation << save_layer_activation;
layers[i]->expectation << save_layer_expectation;
}
}
}
}

| void PLearn::DeepBeliefNet::onlineStep | ( | const Mat & | inputs, |
| const Mat & | targets, | ||
| Mat & | train_costs | ||
| ) |
Definition at line 1704 of file DeepBeliefNet.cc.
References activations_gradients, cd_decrease_ct, cd_learning_rate, PLearn::TMat< T >::clear(), PLearn::TVec< T >::clear(), PLearn::TMat< T >::column(), connections, contrastiveDivergenceStep(), expectations_gradients, PLearn::fast_exact_is_equal(), final_cost, final_cost_gradients, final_cost_index, final_cost_inputs, final_cost_values, final_module, grad_decrease_ct, grad_learning_rate, greedy_target_layers, i, PLearn::TVec< T >::isEmpty(), layers, PLearn::TMat< T >::length(), PLearn::TVec< T >::length(), n_layers, partial_costs, partial_costs_indices, PLERROR, reconstruct_layerwise, reconstruction_cost_index, PLearn::TMat< T >::resize(), PLearn::TVec< T >::resize(), save_layer_activations, save_layer_expectations, PLearn::PLearner::stage, PLearn::TMat< T >::subMatColumns(), top_layer_joint_cd, use_classification_cost, and PLearn::TMat< T >::width().
{
real lr;
// TODO Can we avoid this memory allocation?
TVec<Mat> cost;
Vec optimized_cost(inputs.length());
if (partial_costs) {
cost.resize(n_layers-1);
}
if( greedy_target_layers.length() )
PLERROR("In DeepBeliefNet::onlineStep(): greedy_target_layers not implemented\n"
"for online setting");
layers[0]->setExpectations(inputs);
// FORWARD PHASE
//Vec layer_input;
for( int i=0 ; i<n_layers-1 ; i++ )
{
// mean-field fprop from layer i to layer i+1
connections[i]->setAsDownInputs( layers[i]->getExpectations() );
// this does the actual matrix-vector computation
layers[i+1]->getAllActivations( connections[i], 0, true );
layers[i+1]->computeExpectations();
// propagate into local cost associated to output of layer i+1
if( partial_costs && partial_costs[ i ] )
{
partial_costs[ i ]->fprop( layers[ i+1 ]->getExpectations(),
targets, cost[i] );
// Backward pass
// first time we set these gradients: do not accumulate
optimized_cost << cost[i].column(0); // TODO Can we optimize?
partial_costs[ i ]->bpropUpdate( layers[ i+1 ]->getExpectations(),
targets, optimized_cost,
expectations_gradients[ i+1 ] );
train_costs.subMatColumns(partial_costs_indices[i], cost[i].width())
<< cost[i];
}
else
expectations_gradients[i+1].clear();
}
// top layer may be connected to a final_module followed by a
// final_cost and / or may be used to predict class probabilities
// through a joint classification_module
if ( final_cost )
{
if( final_module )
{
final_module->fprop( layers[ n_layers-1 ]->getExpectations(),
final_cost_inputs );
final_cost->fprop( final_cost_inputs, targets,
final_cost_values );
optimized_cost << final_cost_values.column(0); // TODO optimize
final_cost->bpropUpdate( final_cost_inputs, targets,
optimized_cost,
final_cost_gradients );
final_module->bpropUpdate(
layers[ n_layers-1 ]->getExpectations(),
final_cost_inputs,
expectations_gradients[ n_layers-1 ],
final_cost_gradients, true );
}
else
{
final_cost->fprop( layers[ n_layers-1 ]->getExpectations(),
targets,
final_cost_values );
optimized_cost << final_cost_values.column(0); // TODO optimize
final_cost->bpropUpdate( layers[n_layers-1]->getExpectations(),
targets, optimized_cost,
expectations_gradients[n_layers-1],
true);
}
train_costs.subMatColumns(final_cost_index, final_cost_values.width())
<< final_cost_values;
}
if (final_cost || (!partial_costs.isEmpty() && partial_costs[n_layers-2]))
{
if( !fast_exact_is_equal( grad_decrease_ct, 0. ) )
lr = grad_learning_rate / (1. + grad_decrease_ct * stage );
else
lr = grad_learning_rate;
layers[n_layers-1]->setLearningRate( lr );
connections[n_layers-2]->setLearningRate( lr );
layers[ n_layers-1 ]->bpropUpdate(
layers[ n_layers-1 ]->activations,
layers[ n_layers-1 ]->getExpectations(),
activations_gradients[ n_layers-1 ],
expectations_gradients[ n_layers-1 ],
false);
connections[ n_layers-2 ]->bpropUpdate(
layers[ n_layers-2 ]->getExpectations(),
layers[ n_layers-1 ]->activations,
expectations_gradients[ n_layers-2 ],
activations_gradients[ n_layers-1 ],
true);
// accumulate into expectations_gradients[n_layers-2]
// because a partial cost may have already put a gradient there
}
if( use_classification_cost )
{
PLERROR("In DeepBeliefNet::onlineStep - 'use_classification_cost' not "
"implemented for mini-batches");
/*
classification_module->fprop( layers[ n_layers-2 ]->expectation,
class_output );
real nll_cost;
// This doesn't work. gcc bug?
// classification_cost->fprop( class_output, target, cost );
classification_cost->CostModule::fprop( class_output, target,
nll_cost );
real class_error =
( argmax(class_output) == (int) round(target[0]) ) ? 0: 1;
train_costs[nll_cost_index] = nll_cost;
train_costs[class_cost_index] = class_error;
classification_cost->bpropUpdate( class_output, target, nll_cost,
class_gradient );
classification_module->bpropUpdate( layers[ n_layers-2 ]->expectation,
class_output,
expectation_gradients[n_layers-2],
class_gradient,
true );
if( top_layer_joint_cd )
{
// set the input of the joint layer
Vec target_exp = classification_module->target_layer->expectation;
fill_one_hot( target_exp, (int) round(target[0]), real(0.), real(1.) );
if( !fast_exact_is_equal( cd_decrease_ct, 0. ) )
lr = cd_learning_rate / (1. + cd_decrease_ct * stage );
else
lr = cd_learning_rate;
joint_layer->setLearningRate( lr );
layers[ n_layers-1 ]->setLearningRate( lr );
classification_module->joint_connection->setLearningRate( lr );
save_layer_activation.resize(layers[ n_layers-2 ]->size);
save_layer_activation << layers[ n_layers-2 ]->activation;
save_layer_expectation.resize(layers[ n_layers-2 ]->size);
save_layer_expectation << layers[ n_layers-2 ]->expectation;
contrastiveDivergenceStep(
get_pointer(joint_layer),
get_pointer(classification_module->joint_connection),
layers[ n_layers-1 ], n_layers-2);
layers[ n_layers-2 ]->activation << save_layer_activation;
layers[ n_layers-2 ]->expectation << save_layer_expectation;
}
*/
}
Mat rc;
if (reconstruct_layerwise)
{
rc = train_costs.column(reconstruction_cost_index);
rc.clear();
}
// DOWNWARD PHASE (the downward phase for top layer is already done above,
// except for the contrastive divergence step in the case where either
// 'use_classification_cost' or 'top_layer_joint_cd' is false).
for( int i=n_layers-2 ; i>=0 ; i-- )
{
if (i <= n_layers - 3) {
if( !fast_exact_is_equal( grad_decrease_ct, 0. ) )
lr = grad_learning_rate / (1. + grad_decrease_ct * stage );
else
lr = grad_learning_rate;
connections[ i ]->setLearningRate( lr );
layers[ i+1 ]->setLearningRate( lr );
layers[i+1]->bpropUpdate( layers[i+1]->activations,
layers[i+1]->getExpectations(),
activations_gradients[i+1],
expectations_gradients[i+1] );
connections[i]->bpropUpdate( layers[i]->getExpectations(),
layers[i+1]->activations,
expectations_gradients[i],
activations_gradients[i+1],
true);
}
if (i <= n_layers - 3 || !use_classification_cost ||
!top_layer_joint_cd)
{
// N.B. the contrastiveDivergenceStep changes the activation and
// expectation fields of top layer of the RBM, so it must be
// done last
if( !fast_exact_is_equal( cd_decrease_ct, 0. ) )
lr = cd_learning_rate / (1. + cd_decrease_ct * stage );
else
lr = cd_learning_rate;
layers[i]->setLearningRate( lr );
layers[i+1]->setLearningRate( lr );
connections[i]->setLearningRate( lr );
if( i > 0 )
{
const Mat& source_act = layers[i]->activations;
save_layer_activations.resize(source_act.length(),
source_act.width());
save_layer_activations << source_act;
}
const Mat& source_exp = layers[i]->getExpectations();
save_layer_expectations.resize(source_exp.length(),
source_exp.width());
save_layer_expectations << source_exp;
if (reconstruct_layerwise)
{
connections[i]->setAsUpInputs(layers[i+1]->getExpectations());
layers[i]->getAllActivations(connections[i], 0, true);
layers[i]->fpropNLL(
save_layer_expectations,
train_costs.column(reconstruction_cost_index+i+1));
rc += train_costs.column(reconstruction_cost_index+i+1);
}
contrastiveDivergenceStep( layers[ i ],
connections[ i ],
layers[ i+1 ] ,
i, true);
if( i > 0 )
{
layers[i]->activations << save_layer_activations;
}
layers[i]->getExpectations() << save_layer_expectations;
}
}
}
| int PLearn::DeepBeliefNet::outputsize | ( | ) | const [virtual] |
Returns the size of this learner's output, (which typically may depend on its inputsize(), targetsize() and set options).
Implements PLearn::PLearner.
Definition at line 1022 of file DeepBeliefNet.cc.
References final_module, i_output_layer, layers, n_classes, PLearn::TVec< T >::size(), and use_classification_cost.
Referenced by computeOutput(), and computeOutputsAndCosts().
{
int out_size = 0;
if( use_classification_cost )
out_size += n_classes;
if( final_module )
out_size += final_module->output_size;
if( !use_classification_cost && !final_module )
out_size += layers[i_output_layer]->size;
return out_size;
}


| void PLearn::DeepBeliefNet::setLearningRate | ( | real | the_learning_rate | ) | [private] |
Definition at line 3538 of file DeepBeliefNet.cc.
References classification_module, connections, final_cost, final_module, generative_connections, greedy_target_connections, greedy_target_layers, i, joint_layer, layers, PLearn::TVec< T >::length(), n_layers, partial_costs, and use_classification_cost.
Referenced by train().
{
for( int i=0 ; i<n_layers-1 ; i++ )
{
layers[i]->setLearningRate( the_learning_rate );
connections[i]->setLearningRate( the_learning_rate );
if( partial_costs.length() != 0 && partial_costs[i] )
partial_costs[i]->setLearningRate( the_learning_rate );
}
layers[n_layers-1]->setLearningRate( the_learning_rate );
if( use_classification_cost )
{
classification_module->joint_connection->setLearningRate(
the_learning_rate );
joint_layer->setLearningRate( the_learning_rate );
}
if( final_module )
final_module->setLearningRate( the_learning_rate );
if( final_cost )
final_cost->setLearningRate( the_learning_rate );
for( int i=0 ; i<generative_connections.length() ; i++ )
generative_connections[i]->setLearningRate( the_learning_rate );
for( int i=0; i<greedy_target_connections.length(); i++ )
greedy_target_connections[i]->setLearningRate( the_learning_rate );
for( int i=0; i<greedy_target_layers.length(); i++ )
greedy_target_layers[i]->setLearningRate( the_learning_rate );
}


| void PLearn::DeepBeliefNet::test | ( | VMat | testset, |
| PP< VecStatsCollector > | test_stats, | ||
| VMat | testoutputs = 0, |
||
| VMat | testcosts = 0 |
||
| ) | const [virtual] |
Re-implementation of the PLearner test() for profiling purposes.
Reimplemented from PLearn::PLearner.
Definition at line 3471 of file DeepBeliefNet.cc.
References cumulative_testing_time, cumulative_testing_time_cost_index, PLearn::Profiler::end(), PLearn::Profiler::getStats(), getTestCostNames(), MISSING_VALUE, PLearn::Profiler::reset(), PLearn::Profiler::start(), PLearn::Profiler::Stats::system_duration, PLearn::PLearner::test(), PLearn::Profiler::ticksPerSecond(), and PLearn::Profiler::Stats::user_duration.
{
// Re-implementing simply because we want to measure the time it takes to
// do the testing. The reset is there for two purposes:
// 1. to have fine-grained statistics at each call of test()
// 2. to be able to have a more meaningful cumulative_testing_time
//
// BIG Nota Bene:
// Get the statistics by E[testN.E[cumulative_test_time], where N is the
// index of the last split that you're testing.
// E[testN-1.E[cumulative_test_time] will basically be the cumulative test
// time until (and including) the N-1th split! So it's a pretty
// meaningless number (more or less).
Profiler::reset("testing");
Profiler::start("testing");
inherited::test(testset, test_stats, testoutputs, testcosts);
Profiler::end("testing");
const Profiler::Stats& stats = Profiler::getStats("testing");
real ticksPerSec = Profiler::ticksPerSecond();
real cpu_time = (stats.user_duration+stats.system_duration)/ticksPerSec;
cumulative_testing_time += cpu_time;
if (testcosts)
// if it is used (usually not) testcosts is a VMat that is of size
// nexamples x ncosts. The last column will have missing values.
// We just need to put a value in one of the rows of that column.
testcosts->put(0,cumulative_testing_time_cost_index,cumulative_testing_time);
if( !test_stats )
{
test_stats = new VecStatsCollector();
test_stats->setFieldNames(getTestCostNames());
}
if (test_stats) {
// Here we simply update the corresponding stat index
Vec test_time_stats(test_stats->length(), MISSING_VALUE);
test_time_stats[cumulative_testing_time_cost_index] =
cumulative_testing_time;
test_stats->update(test_time_stats);
test_stats->finalize();
}
}
| void PLearn::DeepBeliefNet::train | ( | ) | [virtual] |
The role of the train method is to bring the learner up to stage==nstages, updating the train_stats collector with training costs measured on-line in the process.
Implements PLearn::PLearner.
Definition at line 1084 of file DeepBeliefNet.cc.
References activations_gradients, background_gibbs_update_ratio, batch_size, PLearn::RBMMatrixTransposeConnection::build(), c, cd_decrease_ct, cd_learning_rate, classification_module, classname(), PLearn::VMat::column(), connections, cumulative_schedule, cumulative_training_time, cumulative_training_time_cost_index, deepCopy(), down_sample, PLearn::Profiler::end(), PLearn::endl(), expectations_gradients, PLearn::fast_exact_is_equal(), PLearn::TMat< T >::fill(), final_cost, final_cost_gradients, fineTuningStep(), generative_connections, PLearn::VMat::getExample(), PLearn::Profiler::getStats(), getTrainCostNames(), gibbs_chain_reinit_freq, gibbs_down_state, grad_decrease_ct, grad_learning_rate, greedy_joint_connections, greedy_joint_layers, greedy_target_connections, greedy_target_layers, greedyStep(), i, initialize_gibbs_chain, PLearn::PLearner::initTrain(), PLearn::PLearner::inputsize(), joint_layer, jointGreedyStep(), layers, learnerExpdir, PLearn::TVec< T >::length(), PLearn::VMat::length(), PLearn::min(), minibatch_hack, minibatch_size, MISSING_VALUE, n_layers, PLearn::PLearner::nstages, online, onlineStep(), optimized_costs, PLASSERT, PLASSERT_MSG, PLWARNING, PLearn::RBMMatrixTransposeConnection::rbm_matrix_connection, reconstruct_layerwise, reconstruction_cost_index, PLearn::Profiler::report(), PLearn::PLearner::report_progress, PLearn::Profiler::reset(), PLearn::TMat< T >::resize(), PLearn::TVec< T >::resize(), PLearn::sample(), PLearn::Object::save(), save_learner_before_fine_tuning, setLearningRate(), PLearn::PLearner::stage, PLearn::Profiler::start(), PLearn::Profiler::Stats::system_duration, PLearn::PLearner::targetsize(), PLearn::Profiler::ticksPerSecond(), PLearn::tostring(), PLearn::PLearner::train_set, PLearn::PLearner::train_stats, train_stats_window, training_cpu_time_cost_index, training_schedule, up_down_decrease_ct, up_down_learning_rate, up_down_nstages, up_down_stage, up_sample, upDownStep(), use_classification_cost, PLearn::Profiler::Stats::user_duration, PLearn::PLearner::verbosity, and w.
{
MODULE_LOG << "train() called " << endl;
if (!online)
{
// Enforce value of cumulative_schedule because build_() might
// not be called if we change training_schedule inside a HyperLearner
for( int i=0 ; i<n_layers ; i++ )
cumulative_schedule[i+1] = cumulative_schedule[i] +
training_schedule[i];
}
MODULE_LOG << " training_schedule = " << training_schedule << endl;
MODULE_LOG << " cumulative_schedule = " << cumulative_schedule << endl;
MODULE_LOG << "stage = " << stage
<< ", target nstages = " << nstages << endl;
PLASSERT( train_set );
int n_train_stats_samples = (train_stats_window >= 0)
? train_stats_window
: train_set->length();
// Training set-dependent initialization.
minibatch_size = batch_size > 0 ? batch_size : train_set->length();
for (int i = 0 ; i < n_layers; i++)
{
activations_gradients[i].resize(minibatch_size, layers[i]->size);
expectations_gradients[i].resize(minibatch_size, layers[i]->size);
if (background_gibbs_update_ratio>0 && i<n_layers-1)
gibbs_down_state[i].resize(minibatch_size, layers[i]->size);
}
if (final_cost)
final_cost_gradients.resize(minibatch_size, final_cost->input_size);
optimized_costs.resize(minibatch_size);
Vec input( inputsize() );
Vec target( targetsize() );
real weight; // unused
Mat inputs(minibatch_size, inputsize());
Mat targets(minibatch_size, targetsize());
Vec weights;
TVec<string> train_cost_names = getTrainCostNames() ;
Vec train_costs( train_cost_names.length() );
Mat train_costs_m(minibatch_size, train_cost_names.length());
train_costs.fill(MISSING_VALUE) ;
train_costs_m.fill(MISSING_VALUE);
int nsamples = train_set->length();
if( !initTrain() )
{
MODULE_LOG << "train() aborted" << endl;
return;
}
PP<ProgressBar> pb;
// Start the actual time counting
Profiler::reset("training");
Profiler::start("training");
// clear stats of previous epoch
train_stats->forget();
if (online)
{
// Train all layers simultaneously AND fine-tuning as well!
int init_stage = stage;
if( report_progress && stage < nstages )
pb = new ProgressBar( "Training "+classname(),
nstages - init_stage );
setLearningRate( grad_learning_rate );
train_stats->forget();
for( ; stage < nstages; stage++)
{
initialize_gibbs_chain=(stage%gibbs_chain_reinit_freq==0);
// Do a step every 'minibatch_size' examples.
if (stage % minibatch_size == 0)
{
int sample_start = stage % nsamples;
if( !fast_exact_is_equal( grad_decrease_ct, 0. ) )
setLearningRate( grad_learning_rate
/ (1. + grad_decrease_ct * stage ));
if (minibatch_size > 1 || minibatch_hack)
{
train_set->getExamples(sample_start, minibatch_size,
inputs, targets, weights, NULL, true);
train_costs_m.fill(MISSING_VALUE);
if (reconstruct_layerwise)
train_costs_m.column(reconstruction_cost_index).clear();
onlineStep( inputs, targets, train_costs_m );
}
else
{
train_set->getExample(sample_start, input, target, weight);
onlineStep( input, target, train_costs );
}
// Update stats if we are in the last n_train_stats_samples
if (stage >= nstages - n_train_stats_samples){
if (minibatch_size > 1 || minibatch_hack)
for (int k = 0; k < minibatch_size; k++)
train_stats->update(train_costs_m(k));
else
train_stats->update(train_costs);
}
}
if( pb )
pb->update( stage - init_stage + 1 );
}
}
else // Greedy learning, one layer at a time.
{
/***** initial greedy training *****/
for( int i=0 ; i<n_layers-1 ; i++ )
{
if( use_classification_cost && i == n_layers-2 )
break; // we will do a joint supervised learning instead
int end_stage = min(cumulative_schedule[i+1], nstages);
if( stage >= end_stage )
continue;
MODULE_LOG << "Training connection weights between layers " << i
<< " and " << i+1 << endl;
MODULE_LOG << " stage = " << stage << endl;
MODULE_LOG << " end_stage = " << end_stage << endl;
MODULE_LOG << " cd_learning_rate = " << cd_learning_rate << endl;
if( report_progress )
pb = new ProgressBar( "Training layer "+tostring(i)
+" of "+classname(),
end_stage - stage );
layers[i]->setLearningRate( cd_learning_rate );
connections[i]->setLearningRate( cd_learning_rate );
layers[i+1]->setLearningRate( cd_learning_rate );
if( greedy_target_layers.length() && greedy_target_layers[i] )
greedy_target_layers[i]->setLearningRate( cd_learning_rate );
if( greedy_target_connections.length() && greedy_target_connections[i] )
greedy_target_connections[i]->setLearningRate( cd_learning_rate );
if( greedy_joint_layers.length() && greedy_joint_layers[i] )
greedy_joint_layers[i]->setLearningRate( cd_learning_rate );
if( greedy_joint_connections.length() && greedy_joint_connections[i] )
greedy_joint_connections[i]->setLearningRate( cd_learning_rate );
for( ; stage<end_stage ; stage++ )
{
if( !fast_exact_is_equal( cd_decrease_ct, 0. ) )
{
real lr = cd_learning_rate
/ (1. + cd_decrease_ct *
(stage - cumulative_schedule[i]));
layers[i]->setLearningRate( lr );
connections[i]->setLearningRate( lr );
layers[i+1]->setLearningRate( lr );
if( greedy_target_layers.length() && greedy_target_layers[i] )
greedy_target_layers[i]->setLearningRate( lr );
if( greedy_target_connections.length() && greedy_target_connections[i] )
greedy_target_connections[i]->setLearningRate( lr );
if( greedy_joint_layers.length() && greedy_joint_layers[i] )
greedy_joint_layers[i]->setLearningRate( lr );
if( greedy_joint_connections.length() && greedy_joint_connections[i] )
greedy_joint_connections[i]->setLearningRate( lr );
}
initialize_gibbs_chain=(stage%gibbs_chain_reinit_freq==0);
// Do a step every 'minibatch_size' examples.
if (stage % minibatch_size == 0) {
int sample_start = stage % nsamples;
if (minibatch_size > 1 || minibatch_hack) {
train_set->getExamples(sample_start, minibatch_size,
inputs, targets, weights, NULL, true);
train_costs_m.fill(MISSING_VALUE);
if (reconstruct_layerwise)
train_costs_m.column(reconstruction_cost_index).clear();
greedyStep( inputs, targets, i , train_costs_m);
for (int k = 0; k < minibatch_size; k++)
train_stats->update(train_costs_m(k));
} else {
train_set->getExample(sample_start, input, target, weight);
greedyStep( input, target, i );
}
}
if( pb )
pb->update( stage - cumulative_schedule[i] + 1 );
}
}
// possible supervised part
int end_stage = min(cumulative_schedule[n_layers-1], nstages);
if( use_classification_cost && (stage < end_stage) )
{
PLASSERT_MSG(batch_size == 1, "'use_classification_cost' code not "
"verified with mini-batch learning yet");
MODULE_LOG << "Training the classification module" << endl;
MODULE_LOG << " stage = " << stage << endl;
MODULE_LOG << " end_stage = " << end_stage << endl;
MODULE_LOG << " cd_learning_rate = " << cd_learning_rate << endl;
if( report_progress )
pb = new ProgressBar( "Training the classification module",
end_stage - stage );
// set appropriate learning rate
joint_layer->setLearningRate( cd_learning_rate );
classification_module->joint_connection->setLearningRate(
cd_learning_rate );
layers[ n_layers-1 ]->setLearningRate( cd_learning_rate );
int previous_stage = cumulative_schedule[n_layers-2];
for( ; stage<end_stage ; stage++ )
{
if( !fast_exact_is_equal( cd_decrease_ct, 0. ) )
{
real lr = cd_learning_rate /
(1. + cd_decrease_ct *
(stage - cumulative_schedule[n_layers-2]));
joint_layer->setLearningRate( lr );
classification_module->joint_connection->setLearningRate( lr );
layers[n_layers-1]->setLearningRate( lr );
}
initialize_gibbs_chain=(stage%gibbs_chain_reinit_freq==0);
int sample = stage % nsamples;
train_set->getExample( sample, input, target, weight );
jointGreedyStep( input, target );
if( pb )
pb->update( stage - previous_stage + 1 );
}
}
if( up_down_stage < up_down_nstages )
{
if( up_down_stage == 0 )
{
// Untie weights
generative_connections.resize(connections.length()-1);
PP<RBMMatrixConnection> w;
RBMMatrixTransposeConnection* wt;
for(int c=0; c<generative_connections.length(); c++)
{
CopiesMap map;
w = dynamic_cast<RBMMatrixConnection*>((RBMConnection*) connections[c]->deepCopy(map));
wt = new RBMMatrixTransposeConnection();
wt->rbm_matrix_connection = w;
wt->build();
generative_connections[c] = wt;
}
up_sample.resize(n_layers);
down_sample.resize(n_layers);
for( int i=0 ; i<n_layers ; i++ )
{
up_sample[i].resize(layers[i]->size);
down_sample[i].resize(layers[i]->size);
}
}
/***** up-down algorithm *****/
MODULE_LOG << "Up-down gradient descent algorithm" << endl;
MODULE_LOG << " up_down_stage = " << up_down_stage << endl;
MODULE_LOG << " up_down_nstages = " << up_down_nstages << endl;
MODULE_LOG << " up_down_learning_rate = " << up_down_learning_rate << endl;
int init_stage = up_down_stage;
if( report_progress )
pb = new ProgressBar( "Up-down gradient descent algorithm "
+ classname(),
up_down_nstages - init_stage );
setLearningRate( up_down_learning_rate );
train_stats->forget();
int sample_start;
for( ; up_down_stage<up_down_nstages ; up_down_stage++ )
{
sample_start = up_down_stage % nsamples;
if( !fast_exact_is_equal( up_down_decrease_ct, 0. ) )
setLearningRate( up_down_learning_rate
/ (1. + up_down_decrease_ct *
up_down_stage) );
train_set->getExample( sample_start, input, target, weight );
upDownStep( input, target, train_costs );
train_stats->update( train_costs );
if( pb )
pb->update( up_down_stage - init_stage + 1 );
}
}
if( save_learner_before_fine_tuning )
{
if( learnerExpdir == "" )
PLWARNING("DeepBeliefNet::train() - \n"
"cannot save model before fine-tuning because\n"
"no experiment directory has been set.");
else
PLearn::save(learnerExpdir + "/learner_before_finetuning.psave",*this);
}
/***** fine-tuning by gradient descent *****/
end_stage = min(cumulative_schedule[n_layers], nstages);
if( stage >= end_stage )
return;
MODULE_LOG << "Fine-tuning all parameters, by gradient descent" << endl;
MODULE_LOG << " stage = " << stage << endl;
MODULE_LOG << " end_stage = " << end_stage << endl;
MODULE_LOG << " grad_learning_rate = " << grad_learning_rate << endl;
int init_stage = stage;
if( report_progress )
pb = new ProgressBar( "Fine-tuning parameters of all layers of "
+ classname(),
end_stage - init_stage );
setLearningRate( grad_learning_rate );
train_stats->forget();
for( ; stage < end_stage; stage++)
{
if (stage % minibatch_size == 0)
{
int sample_start = stage % nsamples;
if( !fast_exact_is_equal( grad_decrease_ct, 0. ) )
setLearningRate( grad_learning_rate
/ (1. + grad_decrease_ct *
(stage - cumulative_schedule[n_layers-1])) );
if (minibatch_size > 1 || minibatch_hack)
{
train_set->getExamples(sample_start, minibatch_size, inputs,
targets, weights, NULL, true);
train_costs_m.fill(MISSING_VALUE);
fineTuningStep(inputs, targets, train_costs_m);
}
else
{
train_set->getExample( sample_start, input, target, weight );
fineTuningStep( input, target, train_costs );
}
// Update stats if we are in the last n_train_stats_samples samples
if (stage >= end_stage - n_train_stats_samples){
if (minibatch_size > 1 || minibatch_hack)
for (int k = 0; k < minibatch_size; k++)
train_stats->update(train_costs_m(k));
else
train_stats->update(train_costs);
}
}
if( pb )
pb->update( stage - init_stage + 1 );
}
}
Profiler::end("training");
// The report is pretty informative and therefore quite verbose.
if (verbosity > 1)
Profiler::report(cout);
const Profiler::Stats& stats = Profiler::getStats("training");
real ticksPerSec = Profiler::ticksPerSecond();
real cpu_time = (stats.user_duration+stats.system_duration)/ticksPerSec;
cumulative_training_time += cpu_time;
if (verbosity > 1)
cout << "The cumulative time spent in train() up until now is " << cumulative_training_time << " cpu seconds" << endl;
train_costs.fill(MISSING_VALUE);
train_costs[training_cpu_time_cost_index] = cpu_time;
train_costs[cumulative_training_time_cost_index] = cumulative_training_time;
train_stats->update( train_costs );
train_stats->finalize();
}
| void PLearn::DeepBeliefNet::upDownStep | ( | const Mat & | inputs, |
| const Mat & | targets, | ||
| Mat & | train_costs | ||
| ) |
Definition at line 2346 of file DeepBeliefNet.cc.
References PLCHECK_MSG.
{
PLCHECK_MSG(false, "Not implemented for mini-batches");
}
Definition at line 2269 of file DeepBeliefNet.cc.
References activation_gradients, classification_module, connections, contrastiveDivergenceStep(), down_sample, PLearn::fill_one_hot(), generative_connections, PLearn::get_pointer(), greedy_target_layers, i, joint_layer, layers, PLearn::TVec< T >::length(), n_layers, PLERROR, up_sample, and use_classification_cost.
Referenced by train().
{
if( greedy_target_layers.length() )
PLERROR("In DeepBeliefNet::onlineStep(): greedy_target_layers not implemented\n"
"for up-down setting");
// Up pass
up_sample[0] << input;
for( int i=0 ; i<n_layers-2 ; i++ )
{
connections[i]->setAsDownInput( up_sample[i] );
layers[i+1]->getAllActivations( connections[i] );
layers[i+1]->computeExpectation();
layers[i+1]->generateSample();
up_sample[i+1] << layers[i+1]->sample;
}
// Top RBM update
if( use_classification_cost )
{
Vec target_exp = classification_module->target_layer->expectation;
fill_one_hot( target_exp, (int) round(target[0]), real(0.), real(1.) );
contrastiveDivergenceStep(
get_pointer( joint_layer ),
get_pointer( classification_module->joint_connection ),
layers[ n_layers-1 ], n_layers-2,false);
}
else
{
contrastiveDivergenceStep( layers[ n_layers-2 ],
connections[ n_layers-2 ],
layers[ n_layers-1 ],
n_layers-2, false);
}
down_sample[n_layers-2] << layers[n_layers-2]->sample;
// Down pass
for( int i=n_layers-3 ; i>=0 ; i-- )
{
generative_connections[i]->setAsDownInput( down_sample[i+1] );
layers[i]->getAllActivations( generative_connections[i] );
layers[i]->computeExpectation();
layers[i]->generateSample();
down_sample[i] << layers[i]->sample;
}
// Updates
real nll = 0.; // Actually unused
for( int i=0 ; i<n_layers-2 ; i++ )
{
// Update recognition weights
connections[i]->setAsDownInput( down_sample[i] );
layers[i+1]->getAllActivations( connections[i] );
layers[i+1]->computeExpectation();
layers[i+1]->bpropNLL(down_sample[i+1], nll, activation_gradients[i+1]);
layers[i+1]->update( activation_gradients[i+1] );
connections[i]->bpropUpdate( down_sample[i],
layers[i+1]->activation,
activation_gradients[i],
activation_gradients[i+1]);
// Update generative weights
generative_connections[i]->setAsDownInput( up_sample[i+1] );
layers[i]->getAllActivations( generative_connections[i] );
layers[i]->computeExpectation();
layers[i]->bpropNLL(up_sample[i], nll, activation_gradients[i]);
layers[i]->update( activation_gradients[i] );
generative_connections[i]->bpropUpdate( up_sample[i+1],
layers[i]->activation,
activation_gradients[i+1],
activation_gradients[i]);
}
}

Reimplemented from PLearn::PLearner.
Definition at line 352 of file DeepBeliefNet.h.
TVec<Vec> PLearn::DeepBeliefNet::activation_gradients [mutable, protected] |
Stores the gradient of the cost wrt the activations (at the input of the layers)
Definition at line 371 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), fineTuningStep(), greedyStep(), jointGreedyStep(), makeDeepCopyFromShallowCopy(), onlineStep(), and upDownStep().
TVec<Mat> PLearn::DeepBeliefNet::activations_gradients [mutable, protected] |
For mini-batch.
Definition at line 372 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), fineTuningStep(), greedyStep(), makeDeepCopyFromShallowCopy(), onlineStep(), and train().
Definition at line 223 of file DeepBeliefNet.h.
Referenced by build_(), build_layers_and_connections(), contrastiveDivergenceStep(), declareOptions(), and train().
Training batch size (1=stochastic learning, 0=full batch learning)
Definition at line 95 of file DeepBeliefNet.h.
Referenced by build_(), build_classification_cost(), build_layers_and_connections(), declareOptions(), jointGreedyStep(), onlineStep(), and train().
The decrease constant of the learning rate used during contrastive divergence learning.
Definition at line 73 of file DeepBeliefNet.h.
Referenced by declareOptions(), greedyStep(), jointGreedyStep(), onlineStep(), and train().
The learning rate used during contrastive divergence learning.
Definition at line 69 of file DeepBeliefNet.h.
Referenced by declareOptions(), greedyStep(), jointGreedyStep(), onlineStep(), and train().
Mat PLearn::DeepBeliefNet::cd_neg_down_vals [mutable, protected] |
Definition at line 418 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), and makeDeepCopyFromShallowCopy().
Mat PLearn::DeepBeliefNet::cd_neg_up_vals [mutable, protected] |
Definition at line 419 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), and makeDeepCopyFromShallowCopy().
int PLearn::DeepBeliefNet::class_cost_index [protected] |
Keeps the index of the class_error cost in train_costs.
Definition at line 441 of file DeepBeliefNet.h.
Referenced by build_costs(), computeClassifAndFinalCostsFromOutputs(), computeCostsFromOutputs(), fineTuningStep(), and onlineStep().
Vec PLearn::DeepBeliefNet::class_gradient [mutable, protected] |
Definition at line 398 of file DeepBeliefNet.h.
Referenced by fineTuningStep(), makeDeepCopyFromShallowCopy(), and onlineStep().
Vec PLearn::DeepBeliefNet::class_output [mutable, protected] |
Definition at line 396 of file DeepBeliefNet.h.
Referenced by fineTuningStep(), makeDeepCopyFromShallowCopy(), and onlineStep().
The module computing the classification cost function (NLL) on top of classification_module.
Definition at line 250 of file DeepBeliefNet.h.
Referenced by build_classification_cost(), computeClassifAndFinalCostsFromOutputs(), computeCostsFromOutputs(), declareOptions(), fineTuningStep(), forget(), makeDeepCopyFromShallowCopy(), and onlineStep().
The module computing the probabilities of the different classes.
Definition at line 205 of file DeepBeliefNet.h.
Referenced by build_classification_cost(), computeOutput(), declareOptions(), fineTuningStep(), forget(), jointGreedyStep(), makeDeepCopyFromShallowCopy(), onlineStep(), setLearningRate(), train(), and upDownStep().
The weights of the connections between the layers.
Definition at line 148 of file DeepBeliefNet.h.
Referenced by build_classification_cost(), build_layers_and_connections(), computeOutput(), declareOptions(), fantasizeKTime(), fineTuningStep(), forget(), greedyStep(), jointGreedyStep(), makeDeepCopyFromShallowCopy(), onlineStep(), setLearningRate(), train(), and upDownStep().
Vec PLearn::DeepBeliefNet::corrupted_pos_down_val [mutable, protected] |
Definition at line 414 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), greedyStep(), and makeDeepCopyFromShallowCopy().
The computed cost names.
Definition at line 211 of file DeepBeliefNet.h.
Referenced by build_costs(), computeCostsFromOutputs(), computeOutputsAndCosts(), getTestCostNames(), getTrainCostNames(), and makeDeepCopyFromShallowCopy().
TVec<int> PLearn::DeepBeliefNet::cumulative_schedule [protected] |
Cumulative training schedule.
Definition at line 471 of file DeepBeliefNet.h.
Referenced by build_(), greedyStep(), jointGreedyStep(), makeDeepCopyFromShallowCopy(), and train().
real PLearn::DeepBeliefNet::cumulative_testing_time [mutable, protected] |
Holds the total testing (cpu)time.
Definition at line 468 of file DeepBeliefNet.h.
Referenced by declareOptions(), forget(), and test().
The index of the cumulative testing time cost.
Definition at line 462 of file DeepBeliefNet.h.
Referenced by build_costs(), and test().
real PLearn::DeepBeliefNet::cumulative_training_time [protected] |
Holds the total training (cpu)time.
Definition at line 465 of file DeepBeliefNet.h.
Referenced by declareOptions(), forget(), and train().
The index of the cumulative training time cost.
Definition at line 459 of file DeepBeliefNet.h.
Referenced by build_costs(), and train().
TVec<Vec> PLearn::DeepBeliefNet::down_sample [mutable, protected] |
Definition at line 484 of file DeepBeliefNet.h.
Referenced by makeDeepCopyFromShallowCopy(), train(), and upDownStep().
TVec<Vec> PLearn::DeepBeliefNet::expectation_gradients [mutable, protected] |
Stores the gradient of the cost wrt the expectations (at the output of the layers)
Definition at line 376 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), fineTuningStep(), greedyStep(), jointGreedyStep(), makeDeepCopyFromShallowCopy(), and onlineStep().
TVec< TVec<int> > PLearn::DeepBeliefNet::expectation_indices [protected] |
Indices of the expectation components.
Definition at line 487 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), corrupt_input(), and makeDeepCopyFromShallowCopy().
TVec<Mat> PLearn::DeepBeliefNet::expectations_gradients [mutable, protected] |
For mini-batch.
Definition at line 377 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), fineTuningStep(), greedyStep(), makeDeepCopyFromShallowCopy(), onlineStep(), and train().
The cost function to be applied on top of the DBN (or of final_module if provided).
Its gradients will be backpropagated to final_module, then combined with the one of classification_cost and backpropagated to the layers.
Definition at line 168 of file DeepBeliefNet.h.
Referenced by build_costs(), build_final_cost(), computeClassifAndFinalCostsFromOutputs(), computeCostsFromOutputs(), computeOutput(), declareOptions(), fineTuningStep(), forget(), makeDeepCopyFromShallowCopy(), onlineStep(), setLearningRate(), and train().
Vec PLearn::DeepBeliefNet::final_cost_gradient [mutable, protected] |
Stores the gradient of the cost at the input of final_cost.
Definition at line 401 of file DeepBeliefNet.h.
Referenced by build_final_cost(), fineTuningStep(), makeDeepCopyFromShallowCopy(), and onlineStep().
Mat PLearn::DeepBeliefNet::final_cost_gradients [mutable, protected] |
For mini-batch.
Definition at line 402 of file DeepBeliefNet.h.
Referenced by fineTuningStep(), makeDeepCopyFromShallowCopy(), onlineStep(), and train().
int PLearn::DeepBeliefNet::final_cost_index [protected] |
Keeps the beginning index of the final costs in train_costs.
Definition at line 444 of file DeepBeliefNet.h.
Referenced by build_costs(), computeClassifAndFinalCostsFromOutputs(), computeCostsFromOutputs(), fineTuningStep(), and onlineStep().
Vec PLearn::DeepBeliefNet::final_cost_input [mutable, protected] |
Definition at line 388 of file DeepBeliefNet.h.
Referenced by computeOutput(), fineTuningStep(), makeDeepCopyFromShallowCopy(), and onlineStep().
Mat PLearn::DeepBeliefNet::final_cost_inputs [mutable, protected] |
For mini-batch.
Definition at line 389 of file DeepBeliefNet.h.
Referenced by fineTuningStep(), makeDeepCopyFromShallowCopy(), and onlineStep().
Vec PLearn::DeepBeliefNet::final_cost_output [mutable, protected] |
Definition at line 394 of file DeepBeliefNet.h.
Referenced by makeDeepCopyFromShallowCopy().
Vec PLearn::DeepBeliefNet::final_cost_value [mutable, protected] |
Definition at line 391 of file DeepBeliefNet.h.
Referenced by computeCostsFromOutputs(), fineTuningStep(), makeDeepCopyFromShallowCopy(), and onlineStep().
Mat PLearn::DeepBeliefNet::final_cost_values [mutable, protected] |
For mini-batch.
Definition at line 392 of file DeepBeliefNet.h.
Referenced by computeClassifAndFinalCostsFromOutputs(), fineTuningStep(), makeDeepCopyFromShallowCopy(), and onlineStep().
Optional module that takes as input the output of the last layer (layers[n_layers-1), and its output is fed to final_cost, and concatenated with the one of classification_cost (if present) as output of the learner.
If it is not provided, then the last layer will directly be put as input of final_cost.
Definition at line 162 of file DeepBeliefNet.h.
Referenced by build_final_cost(), computeOutput(), declareOptions(), fineTuningStep(), forget(), makeDeepCopyFromShallowCopy(), onlineStep(), outputsize(), and setLearningRate().
Fraction of components that will be corrupted in function corrupt_input.
Definition at line 192 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), corrupt_input(), and declareOptions().
TVec< PP<RBMConnection> > PLearn::DeepBeliefNet::generative_connections [protected] |
The untied generative weights of the connections between the layers for the up-down algorithm.
Definition at line 481 of file DeepBeliefNet.h.
Referenced by declareOptions(), forget(), makeDeepCopyFromShallowCopy(), setLearningRate(), train(), and upDownStep().
after how many examples should we re-initialize the Gibbs chains (if == INT_MAX, the default then NEVER re-initialize except when stage==0)
Definition at line 232 of file DeepBeliefNet.h.
Referenced by declareOptions(), and train().
TVec<Mat> PLearn::DeepBeliefNet::gibbs_down_state [mutable, protected] |
Store the state of the Gibbs chain for each RBM.
Definition at line 426 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), contrastiveDivergenceStep(), declareOptions(), makeDeepCopyFromShallowCopy(), and train().
The decrease constant of the learning rate used during gradient descent.
Definition at line 87 of file DeepBeliefNet.h.
Referenced by declareOptions(), greedyStep(), jointGreedyStep(), onlineStep(), and train().
The learning rate used during the gradient descent.
Definition at line 84 of file DeepBeliefNet.h.
Referenced by build_final_cost(), declareOptions(), greedyStep(), jointGreedyStep(), onlineStep(), and train().
TVec< PP<RBMConnection> > PLearn::DeepBeliefNet::greedy_joint_connections [mutable, protected] |
Definition at line 386 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), greedyStep(), makeDeepCopyFromShallowCopy(), and train().
TVec< PP<RBMLayer> > PLearn::DeepBeliefNet::greedy_joint_layers [mutable, protected] |
Definition at line 385 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), greedyStep(), makeDeepCopyFromShallowCopy(), and train().
TVec< TVec<Vec> > PLearn::DeepBeliefNet::greedy_target_activation_gradients [mutable, protected] |
Definition at line 383 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), fineTuningStep(), and makeDeepCopyFromShallowCopy().
TVec< TVec<Vec> > PLearn::DeepBeliefNet::greedy_target_activations [mutable, protected] |
Definition at line 381 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), fineTuningStep(), and makeDeepCopyFromShallowCopy().
Optional target matrix connections for greedy layer-wise pretraining.
Definition at line 154 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), computeOutput(), declareOptions(), fineTuningStep(), forget(), greedyStep(), makeDeepCopyFromShallowCopy(), setLearningRate(), and train().
TVec< TVec<Vec> > PLearn::DeepBeliefNet::greedy_target_expectation_gradients [mutable, protected] |
Definition at line 382 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), fineTuningStep(), and makeDeepCopyFromShallowCopy().
TVec< TVec<Vec> > PLearn::DeepBeliefNet::greedy_target_expectations [mutable, protected] |
For the fprop with greedy_target_layers.
Definition at line 380 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), computeOutput(), fineTuningStep(), greedyStep(), and makeDeepCopyFromShallowCopy().
Keeps the beginning index of the greedy target layer NLLs.
Definition at line 453 of file DeepBeliefNet.h.
Referenced by build_costs(), and computeCostsFromOutputs().
Optional target layers for greedy layer-wise pretraining.
Definition at line 151 of file DeepBeliefNet.h.
Referenced by build_costs(), build_layers_and_connections(), computeCostsFromOutputs(), computeOutput(), declareOptions(), fineTuningStep(), forget(), greedyStep(), makeDeepCopyFromShallowCopy(), onlineStep(), setLearningRate(), train(), and upDownStep().
TVec< Vec > PLearn::DeepBeliefNet::greedy_target_probability_gradients [mutable, protected] |
Definition at line 384 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), fineTuningStep(), and makeDeepCopyFromShallowCopy().
The index of the output layer (when the final module is external)
Definition at line 138 of file DeepBeliefNet.h.
Referenced by build_(), computeOutput(), declareOptions(), and outputsize().
bool PLearn::DeepBeliefNet::initialize_gibbs_chain [protected] |
Definition at line 367 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), and train().
Concatenation of layers[n_layers-2] and the target layer (that is inside classification_module), if use_classification_cost.
Definition at line 254 of file DeepBeliefNet.h.
Referenced by build_classification_cost(), declareOptions(), jointGreedyStep(), makeDeepCopyFromShallowCopy(), onlineStep(), setLearningRate(), train(), and upDownStep().
Vec PLearn::DeepBeliefNet::layer_input [mutable, protected] |
Definition at line 476 of file DeepBeliefNet.h.
Referenced by computeOutput(), and makeDeepCopyFromShallowCopy().
Mat PLearn::DeepBeliefNet::layer_inputs [mutable, protected] |
Definition at line 477 of file DeepBeliefNet.h.
Referenced by fineTuningStep(), greedyStep(), and makeDeepCopyFromShallowCopy().
The layers of units in the network.
Definition at line 134 of file DeepBeliefNet.h.
Referenced by build_(), build_classification_cost(), build_final_cost(), build_layers_and_connections(), computeCostsFromOutputs(), computeOutput(), computeOutputsAndCosts(), declareOptions(), fantasizeKTime(), fineTuningStep(), forget(), greedyStep(), jointGreedyStep(), makeDeepCopyFromShallowCopy(), onlineStep(), outputsize(), setLearningRate(), train(), and upDownStep().
Experiment directory where the learner will be save if save_learner_before_fine_tuning is true.
Definition at line 142 of file DeepBeliefNet.h.
Referenced by declareOptions(), and train().
Indication that inputs should be masked with 0 or 1 according to prop_salt_noise.
Definition at line 196 of file DeepBeliefNet.h.
Referenced by corrupt_input(), and declareOptions().
Coefficient between 0 and 1.
0 means CD-1 update only and 1 means MF-CD only. Values in between means a weighted combination of both.
Definition at line 237 of file DeepBeliefNet.h.
Referenced by build_(), contrastiveDivergenceStep(), and declareOptions().
Vec PLearn::DeepBeliefNet::mf_cd_neg_down_val [mutable, protected] |
Definition at line 422 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), and makeDeepCopyFromShallowCopy().
Mat PLearn::DeepBeliefNet::mf_cd_neg_down_vals [mutable, protected] |
Definition at line 420 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), and makeDeepCopyFromShallowCopy().
Vec PLearn::DeepBeliefNet::mf_cd_neg_up_val [mutable, protected] |
Definition at line 423 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), and makeDeepCopyFromShallowCopy().
Mat PLearn::DeepBeliefNet::mf_cd_neg_up_vals [mutable, protected] |
Definition at line 421 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), and makeDeepCopyFromShallowCopy().
int PLearn::DeepBeliefNet::minibatch_size [protected] |
Actual size of a mini-batch (size of the training set if batch_size==1)
Definition at line 362 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), declareOptions(), fineTuningStep(), greedyStep(), and train().
Number of classes in the training set.
Definition at line 102 of file DeepBeliefNet.h.
Referenced by build_classification_cost(), build_costs(), build_final_cost(), build_layers_and_connections(), computeClassifAndFinalCostsFromOutputs(), computeCostsFromOutputs(), computeOutput(), declareOptions(), fineTuningStep(), greedyStep(), and outputsize().
Number of layers.
Definition at line 208 of file DeepBeliefNet.h.
Referenced by build_(), build_classification_cost(), build_costs(), build_final_cost(), build_layers_and_connections(), computeCostsFromOutputs(), computeOutput(), computeOutputsAndCosts(), declareOptions(), DeepBeliefNet(), fantasizeKTime(), fineTuningStep(), forget(), greedyStep(), jointGreedyStep(), onlineStep(), setLearningRate(), train(), and upDownStep().
int PLearn::DeepBeliefNet::nll_cost_index [protected] |
Keeps the index of the NLL cost in train_costs.
Definition at line 438 of file DeepBeliefNet.h.
Referenced by build_costs(), computeClassifAndFinalCostsFromOutputs(), computeCostsFromOutputs(), fineTuningStep(), and onlineStep().
Type of noise that corrupts the pos_down_val.
Definition at line 188 of file DeepBeliefNet.h.
Referenced by build_layers_and_connections(), corrupt_input(), and declareOptions().
whether to do things by stages, including fine-tuning, or on-line
Definition at line 214 of file DeepBeliefNet.h.
Referenced by build_(), build_layers_and_connections(), declareOptions(), and train().
Vec PLearn::DeepBeliefNet::optimized_costs [protected] |
Used to store the costs optimized by the final cost module.
Definition at line 429 of file DeepBeliefNet.h.
Referenced by fineTuningStep(), makeDeepCopyFromShallowCopy(), and train().
The different cost function to be applied on top of each layer (except the first one, which has to be null) of the RBM.
These costs are not back-propagated to previous layers.
Definition at line 173 of file DeepBeliefNet.h.
Referenced by build_costs(), build_layers_and_connections(), computeClassifAndFinalCostsFromOutputs(), computeCostsFromOutputs(), computeOutput(), computeOutputsAndCosts(), declareOptions(), forget(), greedyStep(), jointGreedyStep(), makeDeepCopyFromShallowCopy(), onlineStep(), and setLearningRate().
TVec<int> PLearn::DeepBeliefNet::partial_costs_indices [protected] |
Keeps the beginning indices of the partial costs in train_costs.
Definition at line 447 of file DeepBeliefNet.h.
Referenced by build_costs(), computeCostsFromOutputs(), computeOutputsAndCosts(), makeDeepCopyFromShallowCopy(), and onlineStep().
Vec PLearn::DeepBeliefNet::pos_down_val [mutable, protected] |
Store a copy of the positive phase values.
Definition at line 413 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), and makeDeepCopyFromShallowCopy().
Mat PLearn::DeepBeliefNet::pos_down_vals [mutable, protected] |
Definition at line 416 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), and makeDeepCopyFromShallowCopy().
Vec PLearn::DeepBeliefNet::pos_up_val [mutable, protected] |
Definition at line 415 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), and makeDeepCopyFromShallowCopy().
Mat PLearn::DeepBeliefNet::pos_up_vals [mutable, protected] |
Definition at line 417 of file DeepBeliefNet.h.
Referenced by contrastiveDivergenceStep(), and makeDeepCopyFromShallowCopy().
Probability that we mask by 1 instead of 0 when using mask_with_pepper_salt.
Definition at line 200 of file DeepBeliefNet.h.
Referenced by corrupt_input(), and declareOptions().
Minimize reconstruction error of each layer as an auto-encoder.
This is done using cross-entropy between actual and reconstructed. This option automatically adds the following cost names: layerwise_reconstruction_error (sum over all layers) layer0.reconstruction_error (only layers[0]) layer1.reconstruction_error (only layers[1]) etc.
Definition at line 131 of file DeepBeliefNet.h.
Referenced by build_costs(), computeCostsFromOutputs(), computeOutput(), computeOutputsAndCosts(), declareOptions(), fineTuningStep(), greedyStep(), onlineStep(), and train().
int PLearn::DeepBeliefNet::reconstruction_cost_index [protected] |
Keeps the beginning index of the reconstruction costs in train_costs.
Definition at line 450 of file DeepBeliefNet.h.
Referenced by build_costs(), computeCostsFromOutputs(), computeOutputsAndCosts(), fineTuningStep(), greedyStep(), onlineStep(), and train().
Vec PLearn::DeepBeliefNet::reconstruction_costs [mutable, protected] |
Stores reconstruction costs.
Definition at line 435 of file DeepBeliefNet.h.
Referenced by build_costs(), computeCostsFromOutputs(), computeOutput(), computeOutputsAndCosts(), and makeDeepCopyFromShallowCopy().
Vec PLearn::DeepBeliefNet::save_layer_activation [mutable, protected] |
buffers bottom layer activation during onlineStep
Definition at line 405 of file DeepBeliefNet.h.
Referenced by makeDeepCopyFromShallowCopy(), and onlineStep().
Mat PLearn::DeepBeliefNet::save_layer_activations [protected] |
For mini-batches.
Definition at line 406 of file DeepBeliefNet.h.
Referenced by makeDeepCopyFromShallowCopy(), and onlineStep().
Vec PLearn::DeepBeliefNet::save_layer_expectation [mutable, protected] |
buffers bottom layer expectation during onlineStep
Definition at line 409 of file DeepBeliefNet.h.
Referenced by makeDeepCopyFromShallowCopy(), and onlineStep().
Mat PLearn::DeepBeliefNet::save_layer_expectations [protected] |
For mini-batches.
Definition at line 410 of file DeepBeliefNet.h.
Referenced by makeDeepCopyFromShallowCopy(), and onlineStep().
Saves the learner before the supervised fine_tuning.
Definition at line 145 of file DeepBeliefNet.h.
Referenced by declareOptions(), and train().
Vec PLearn::DeepBeliefNet::target_one_hot [mutable, protected] |
One-hot representation of the target.
Definition at line 432 of file DeepBeliefNet.h.
Referenced by build_costs(), computeCostsFromOutputs(), and makeDeepCopyFromShallowCopy().
Timer for monitoring the speed.
Definition at line 246 of file DeepBeliefNet.h.
Referenced by makeDeepCopyFromShallowCopy().
Wether we do a step of joint contrastive divergence on top-layer Only used if online for the moment.
Definition at line 227 of file DeepBeliefNet.h.
Referenced by declareOptions(), and onlineStep().
The number of samples to use to compute training stats.
-1 (default) means the number of training samples.
Definition at line 241 of file DeepBeliefNet.h.
Referenced by declareOptions(), and train().
Index of the cpu time cost (per each call of train())
Definition at line 456 of file DeepBeliefNet.h.
Referenced by build_costs(), and train().
Number of examples to use during each phase of learning: first the greedy phases, and then the fine-tuning phase.
However, the learning will stop as soon as we reach nstages. For example for 2 hidden layers, with 1000 examples in each greedy phase, and 500 in the fine-tuning phase, this option should be [1000 1000 500], and nstages should be at least 2500. When online = true, this vector is ignored and should be empty.
Definition at line 111 of file DeepBeliefNet.h.
Referenced by build_(), declareOptions(), makeDeepCopyFromShallowCopy(), and train().
The decrease constant of the learning rate used in the up-down algorithm during the unsupervised fine tuning gradient descent.
Definition at line 81 of file DeepBeliefNet.h.
Referenced by declareOptions(), and train().
The learning rate used in the up-down algorithm during the unsupervised fine tuning gradient descent.
Definition at line 77 of file DeepBeliefNet.h.
Referenced by declareOptions(), and train().
Number of samples to use for unsupervised fine-tuning with the up-down algorithm.
The unsupervised fine-tuning will be executed between the greedy layer-wise learning and the supervised fine-tuning.
Definition at line 117 of file DeepBeliefNet.h.
Referenced by build_(), declareOptions(), and train().
int PLearn::DeepBeliefNet::up_down_stage [protected] |
Number of samples visited so far during unsupervised fine-tuning.
Definition at line 474 of file DeepBeliefNet.h.
Referenced by declareOptions(), forget(), and train().
TVec<Vec> PLearn::DeepBeliefNet::up_sample [mutable, protected] |
Definition at line 483 of file DeepBeliefNet.h.
Referenced by makeDeepCopyFromShallowCopy(), train(), and upDownStep().
If the first cost function is the NLL in classification, pre-trained with CD, and using the last *two* layers to get a better approximation (undirected softmax) than layer-wise mean-field.
Definition at line 122 of file DeepBeliefNet.h.
Referenced by build_costs(), build_layers_and_connections(), computeClassifAndFinalCostsFromOutputs(), computeCostsFromOutputs(), computeOutput(), declareOptions(), fineTuningStep(), forget(), onlineStep(), outputsize(), setLearningRate(), train(), and upDownStep().
Indicates whether we will use a corrupted version of the positive down value during the CD step.
"Choose among: - \"for_cd_fprop"
Definition at line 185 of file DeepBeliefNet.h.
Referenced by build_(), build_layers_and_connections(), contrastiveDivergenceStep(), declareOptions(), and greedyStep().
Indication that the update of the top layer during CD uses a sample, not the expectation.
Definition at line 177 of file DeepBeliefNet.h.
Referenced by build_(), contrastiveDivergenceStep(), and declareOptions().
 1.7.4
1.7.4